Расчет трубопроводной арматуры. Часть III. Критерии оценки и анализ результатов расчета

Андрей Кавардак, Михаил Черных, Алексей Чурилов, Алексей Журавлев

Введение

В заключительной статье представлены критерии оценки достижения различных предельных состояний и анализ результатов расчета на примере антипомпажного клапана (далее — арматура) для полностью закрытого положения затвора при нормальных условиях эксплуатации в летнем сезоне. Последовательность создания расчетных моделей для проведения расчетов современными методами приведена в [1].

Предельные состояния

Согласно [2], каждый элемент арматуры должен быть оценен на предотвращение достижения следующих предельных состояний:

• разрушение или пластическая деформация по всему сечению детали (ГК);
• возникновение макротрещины при циклическом нагружении детали (ЦН);
• наличие прогрессирующего формоизменения (ПФ);
• недопустимое изменение размеров элементов по условиям функционирования арматуры (ЭК);
• потеря устойчивости детали (ПУ).

Кроме того, требуется проверка еще одного предельного состояния — локальное разрушение (ЛК), которое возникает при достижении предела трехосной деформации (особенно в зонах концентраций напряжений). Причина необходимости такой проверки связана с тем, что используемые в нормативно­технической документации критерии, основанные на эквивалентных напряжениях Мизеса или Треска, никак не ограничивают гидростатическое напряжение, то есть тот случай, когда напряжения на главных площадках одинаковы. Таким образом, для полноты картины вводится дополнительная проверка на алгебраическую сумму главных напряжений. В случае вязких материалов (при температурах, не вызывающих ползучесть) используется ограничение не напряжений, а деформаций, что является более точным ([3]).

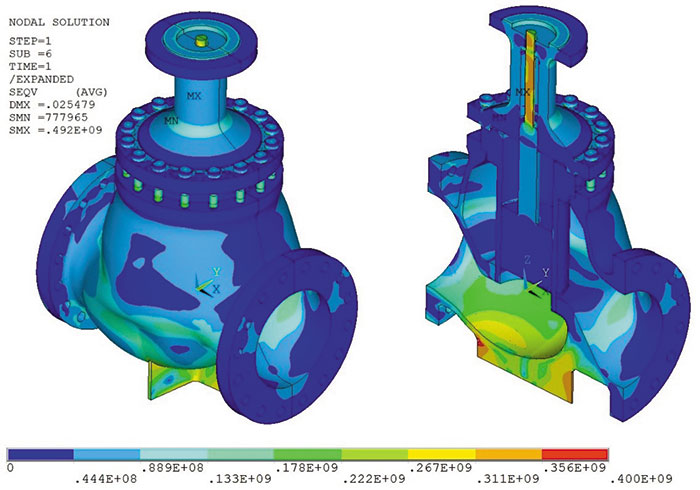
Рис. 1. Карта распределения эквивалентных напряжений по Мизесу, Па

Критерии оценки и анализ результатов

Как правило, существует несколько вариантов критериев оценки достижения предельных состояний. В данной статье будут рассмотрены наиболее предпочтительные и применимые на практике критерии при расчете методом конечных элементов.

Проверку предельных состояний необходимо проводить с учетом влияния геометрической нелинейности, а также с применением условия текучести Мизеса и связанным с ним ассоциированным законом пластического течения.

Предельные состояния ГК и ПУ не достигаются, когда при различных комбинациях расчетных нагрузок с учетом коэффициентов перегрузки (минимально необходимый перечень приведен в [4],
табл. 5.5) эквивалентные напряжения по Мизесу не достигают значения истинного предела прочности и не происходит общей потери устойчивости конструкции, то есть не складывается такая ситуация, когда решение перестает сходиться даже при незначительном увеличении нагрузки. При этом геометрические несовершенства конструкции должны быть адекватно отражены в модели.

Для расчета используется упруго­пластическая диаграмма материала. Результаты расчета для одной из комбинаций расчетных нагрузок представлены на рис. 1.

Поскольку решение сошлось, и уровень эквивалентных напряжений оказался меньше истинного предела прочности, то разрушение или пластическая деформация по всему сечению детали, а также потеря устойчивости отсутствуют.

Предельное состояние ЭК не достигается, когда при различных комбинациях расчетных нагрузок, заданных в технических требованиях к арматуре, не происходит превышения допустимой деформации или перемещений. Для расчета используется упруго­пластическая диаграмма материала.

Специальные требования в данном случае заданы не были, поэтому оценка не проводилась.

Предельное состояние ЛК не достигается, когда удовлетворяется следующее условие ([4], п. 5.3.3.1, ф. 5.7):

, где

объемная деформация εL определяется по [4], ф. 5.6:

.

Значения деформации формоизменения в холодном состоянии εcf, предела одноосной деформации εLu, коэффициента для предела многоосной деформации αsl и коэффициента m2 принимаются в соответствии с [4], табл. 5.7, а значения эквивалентных пластических деформаций εpeq, главных напряжений σ1, σ2, σ3 и эквивалентных напряжений σe определяются по результатам расчета.

Для удобства оценки рекомендуется ввести параметр LCRIT:

.

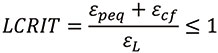
Расчет необходимо проводить только на действие постоянных расчетных нагрузок с учетом коэффициента перегрузки, равного 1,7.

Для расчета используется упруго­пластическая диаграмма материала; результаты расчета представлены на рис. 2.

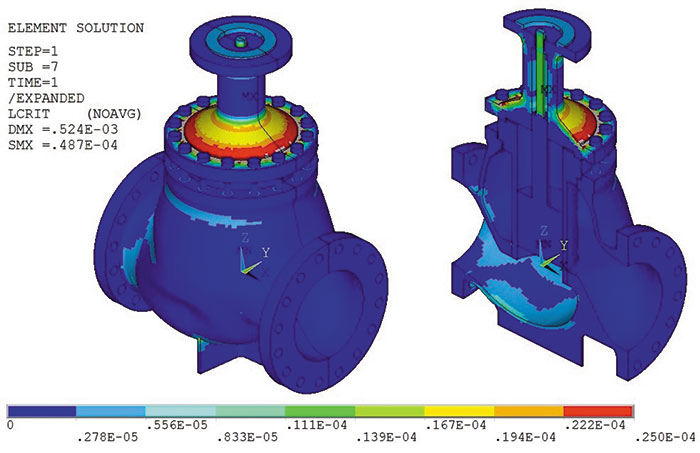
Поскольку LCRIT ≤ 1, то локального разрушения не происходит.

Предельное состояние ПФ не достигается, когда удовлетворяется хотя бы одно из следующих условий в каждой точке после необходимого повторения циклов:

• отсутствуют пластические деформации;
• присутствует упругое ядро;
• отсутствуют постоянные изменения в размерах элементов, то есть движение гистерезисной петли «напряжение — деформация» вдоль оси деформации не поддерживается и происходит ее стабилизация. Для подтверждения данного условия рекомендуется выводить карты разности пластических деформаций между последним и предпоследним циклом.

Расчет выполняется путем приложения, снятия и повторного приложения расчетных нагрузок (не менее трех циклов). В случае если количества выполненных повторений для проведения оценки недостаточно, их число необходимо увеличить.

Для расчета используется упруго­идеальнопластическая диаграмма материала; результаты расчета представлены на рис. 3.

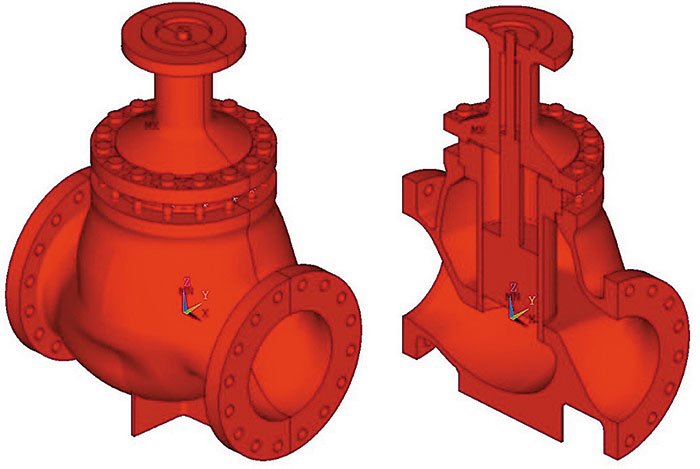
Рис. 3. Карта распределения эквивалентной пластической деформации

Поскольку в арматуре отсутствуют пластические деформации, то прогрессирующего формоизменения не происходит.

Предельное состояние ЦН не достигается, когда накопленная поврежденность SUMDAM от каждого вида цикла в сумме не превышает единицу.

Для определения накопленной поврежденности используется метод двойной текучести. В данном методе анализ напряжений выполняется после одного этапа нагружения, который представляет собой цикл, то есть прикладывается размах нагрузок (разность расчетных нагрузок между началом и концом цикла), а свойства материала принимаются при средней температуре цикла. Однако поскольку диаграмма материала имеет нелинейный характер, то для более точного моделирования рекомендуется определять размах напряжений и деформаций как разность соответствующих параметров между началом и концом цикла соответственно при начальных и конечных расчетных нагрузках и температурах.

Последовательность определения накопленной поврежденности для одного вида цикла согласно [4], п. 5.5.4 приведена ниже.

Сначала по результатам расчета определяются размахи эквивалентных напряжений ∆Sp и пластических деформаций ∆εpeq на основании размахов компонентов тензоров напряжения ∆σij и пластической деформации ∆pij:

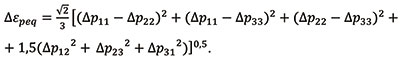
После этого вычисляется размах эффективной деформации ∆εeff и знакопеременное эквивалентное напряжение Salt:

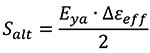
 , где

Eya — модуль упругости I рода.

Для определения допускаемого количества циклов N используются кривые усталости, заданные следующим уравнением:

N = 10x, где

показатель X и коэффициент напряжений Y рассчитываются по формулам:

.

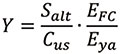Значения констант Ci, коэффициента пересчета Cus и модуля упругости EFC зависят от типа материала и принимаются согласно [4], прил. 3­F. Пример построенной таким образом кривой усталости при температуре 20 °С приведен на рис. 4.

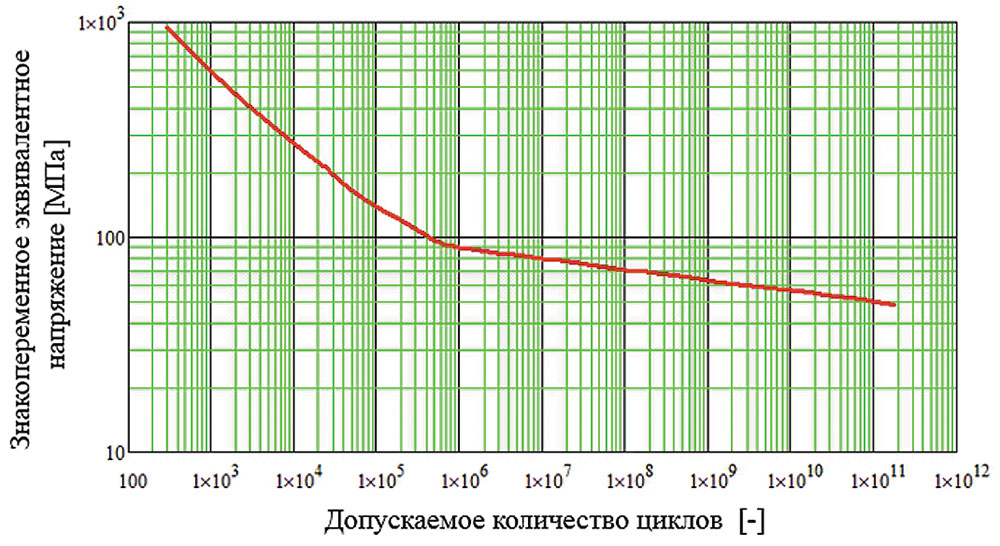
Рис. 4. Кривая усталости для материала корпуса арматуры

SUMDAM определяется как отношение наработанного количества циклов данного типа n к допускаемому:

.

Для упрощения оценки результатов расчета рекомендуется выводить карты распределения SUMDAM непосредственно в программе конечно­элементного анализа. Например, в ANSYS для этого можно использовать специально созданный макрос.

Для расчета используется циклическая диаграмма материала, результаты расчета представлены на рис. 5.

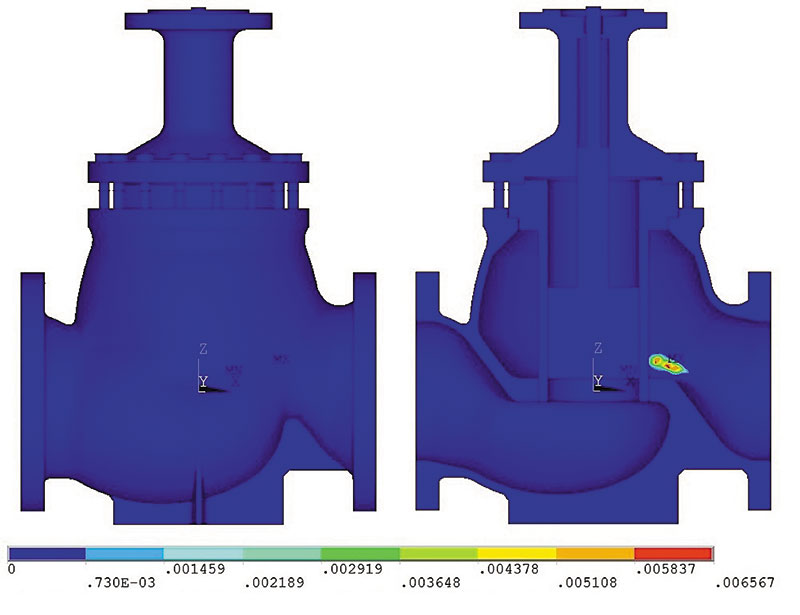
Рис. 5. Карта распределения SUMDAM

Поскольку SUMDAM ≤ 1, то трещина не образуется.

Проведенные поверочные расчеты показывают, что в арматуре не возникают вышеприведенные предельные состояния при нормальных условиях эксплуатации и заданных расчетных нагрузках.

Заключение

Расчет статической и циклической прочности позволяет провести оценку напряженно­деформированного состояния и прогнозировать ресурс арматуры. На основании результатов расчетов возможна разработка рекомендаций по изменению геометрии арматуры с целью получения равнопрочной конструкции, что приведет к экономии материала.

С примером полного технического отчета, содержащего все результаты проведенных расчетов по оценке предельных состояний арматуры современными методами, можно ознакомиться на сайте [5].

Список использованной литературы

1. Кавардак А., Черных М., Чурилов А., Журавлев А. Расчет трубопроводной арматуры. Часть II. Создание расчетной модели // САПР и графика. 2016. № 4. С. 12­14.
2. Кавардак А., Черных М., Чурилов А., Журавлев А. Расчет трубопроводной арматуры. Часть I. Преимущества расчета современными методами // САПР и графика. 2016. № 3. С. 78­80.
3. PTB­1­2014. ASME Section VIII — Division 2. Criteria and Commentary.
4. ASME BPVC. Section VIII. Division 2. 2015. ASME Boiler and Pressure Vessel Code AN INTERNATIONAL CODE. VIII Rules for Construction of Pressure Vessels. Division 2 Alternative Rules.
5. CAE­CUBE: [Электронный ресурс]. URL: http://cae­cube.ru/ (дата обращения — 16.02.2016).

САПР и графика 5`2016