Определение облика изделия с помощью программного комплекса pSeven в среде управления инженерными данными Teamcenter

Геннадий Крылов
Заместитель начальника отдела автоматизации конструкторского проектирования ОАО «Конструкторское бюро приборостроения»
Андрей Сарычев
Ведущий инженер-конструктор
ОАО «Конструкторское бюро приборостроения»
Дмитрий Хоминич
Руководитель отдела решения прикладных задач ООО «Датадванс»
Антон Кавалеров
Ведущий специалист CAE, консалтинговая группа «Борлас»

Автоматизация процессов проектирования, в том числе проведение многодисциплинарных обликовых исследований и решение обратных (оптимизационных) конструкторских задач, является вопросом исключительной важности. В статье представлено комплексное решение этой проблемы, основанное на тесной интеграции программного комплекса (ПК) pSeven с системой управления расчетными данными PLM Teamcenter. В предложенной схеме ПК pSeven предоставляет исчерпывающий набор эффективных алгоритмов оптимизации и анализа данных, а также широкие интеграционные возможности, позволяющие легко включать в расчетные модели различные вычислительные модули (коммерческие и/или собственной разработки). При этом полное представление исходных данных и результатов всех проводимых расчетов, включая управление версионностью и разграничение прав доступа, обеспечивается PLM Teamcenter. Эффективность предлагаемого решения продемонстрирована в задаче определения оптимального облика высокоточного боеприпаса, в которой применение автоматизированных средств проектирования не только существенно сокращает время разработки, но и позволяет найти принципиально новые конструкторские решения.

Введение

Опыт локальных военных конфликтов последнего времени убедительно свидетельствует о всё возрастающей роли и эффективности применения высокоточного оружия (ВТО). По эффективности поражения целей ВТО уже сейчас приближается к тактическому ядерному оружию, не создавая при этом негативных эффектов, сопутствующих использованию оружия массового поражения. В силу этого первоочередными задачами на современном этапе становятся задачи проектирования высокоточных боеприпасов (ВТБ) для ракетного вооружения и артиллерии (РВиА). Примером сложности проектирования ВТБ может служить задача выбора параметров системы управления полетом и характеристик планера ВТБ, обеспечивающих оптимальный угол подхода к цели. При этом должны выполняться противоречивые требования, например превышение по высоте зоны действия комплексов активной защиты (КАЗ) объектов бронетанковой техники (ОБТТ) и обеспечение требуемой дальности захвата цели в условиях низкой облачности.

Таким образом, решение задач современного проектирования ВТБ невозможно без использования формализованных методов автоматизированного поиска оптимальных проектных решений. Эта задача обладает достаточно большим числом проектных параметров, требует учета разнообразных физических процессов (аэродинамики, баллистики, динамики полета, прочности и др.), а следовательно, использования различных математических моделей и соответствующих программных пакетов. Кроме того, необходимо учитывать в том или ином приближении различные внешние факторы (погодные условия, движение цели и др.). Другими словами, эта задача является многопараметрической многокритериальной оптимизационной задачей с ограничениями, которая рассматривается в условиях неопределенности. На детальном (рабочем) уровне проектирования задача не становится проще, наоборот, степень технической сложности возрастает. Отсюда следует, что без использования формализованных критериев и автоматизации всего процесса эффективное проектирование при современных предъявляемых требованиях невозможно ни на концептуальном, ни на рабочем уровне.

Успешное решение задачи совершенствования тактико­технических характеристик ВТБ РВиА зачастую требует многократного пересмотра структуры изделия как на концептуальном, так и на детальном уровне проектирования. Анализ этих задач показывает, что они имеют общий характер, при этом одной из наиболее сложных является задача определения оптимального облика и состава изделия на ранних этапах проектирования. Это связано, прежде всего, со следующими специфическими особенностями ВТБ:

• малые габариты, большие эксплуатационные нагрузки и высокая насыщенность изделия различными функциональными элементами;
• наличие взаимодействующих между собой подсистем, что требует использования многодисциплинарного подхода к моделированию (необходимости одновременно учитывать аэродинамику, прочность, баллистику, эффективность и т.д.).

Сегодня не существует сколь­нибудь универсальных методик решения описанных выше задач. Целью настоящей работы является частичное заполнение этого пробела, а именно — решается модельная многодисциплинарная задача поиска оптимальной компоновки ВТБ, удовлетворяющей целому ряду ограничений (прогнозируемая эффективность применения, располагаемые перегрузки, технологические требования).

Необходимо отметить, что решаемая в данной работе задача является модельной, постановка и ограничения были преднамеренно искажены по соображениям конфиденциальности. Тем не менее остальные аспекты исследования выдержаны максимально близкими к реалистичному сценарию, в котором такая работа выполнялась бы силами специалистов Тульского КБ Приборостроения (КБП). При этом в силу большого числа привлекаемых специалистов, работающих в различных подразделениях предприятия, возникают специфические сложности крупномасштабного применения автоматизированных процессов проектирования. Например, подготовка задачи, выбор адекватных моделей и нахождение решения практически всегда являются итеративных процессом, требующим взаимодействия многих людей (необходимо подготовить параметрическую модель изделия и соответствующие расчетные модели, связать модели в единую расчетную цепочку, отладить процесс ее исполнения, а также периодически вносить корректировки на всех стадиях по ходу отработки изделия). Процесс построения решения зачастую включает различные виды вспомогательных исследований, которыми занимаются специалисты разных подразделений. Всё это требует координации действия сотрудников, четкого разграничения прав доступа, надежного хранения расчетных моделей и вспомогательных материалов. В рамках большого предприятия это означает необходимость внедрения полноценной PLM­системы, которая позволяет не только разрешить означенные проблемы в рамках всего предприятия, но одновременно с тем формализовать и автоматизировать процессы проектирования, сохранить опыт проведения подобных исследований для будущих поколений конструкторов. Актуальность и ценность такой формализации трудно переоценить, учитывая всё увеличивающийся разрыв поколений на многих предприятиях ОПК.

В настоящем исследовании компания DATADVANCE [1] совместно с компанией «Борлас» [2] выполнила интеграцию программного комплекса для проведения различных видов оптимизационных расчетов pSeven с системой управления расчетными данными Teamcenter for Simualtion (модуль PLM системы Teamcenter (TC)). В данной работе помимо решения задачи поиска оптимальной компоновки также рассматривается вопрос о том, как происходит работа в такой интегрированной среде.

Постановка задачи

Рассматриваемая в данной работе задача заключается в нахождении оптимальной аэродинамической компоновки противотанковой управляемой ракеты (ПТУР), обеспечивающей максимальную боевую эффективность при минимальном усложнении конструкции по сравнению с существующими изделиями. В такой общей постановке задача, конечно же, не поддается решению, как минимум, необходимо количественно определить понятия «эффективности» и «степени усложнения». Использованные в данной работе упрощающие предположения сводятся к следующим:

• ?эффективность.

Предполагается, что максимальная боевая эффективность достигается при подходе ПТУР к ОБТТ «сверху», в обход зоны действия КАЗ, с конечным допустимым углом отклонения от вертикали. Траектория полета при этом представляет собой последовательность участков, схематично показанных на рис. 1: короткий стартовый участок 1, горизонтальный участок полета 2, «горка» (набор высоты с постоянной перегрузкой — участок 3), прямолинейный набор высоты на участке 4 и пропорциональное сближение на участке 5;

• ?степень усложнения.

Предполагается, что степень усложнения изделия останется приемлемо малой, если достижение максимальной эффективности не потребует введения дополнительных средств управления (интерцепторов, газовых рулей, устройства отклонения вектора тяги либо импульсных двигателей).

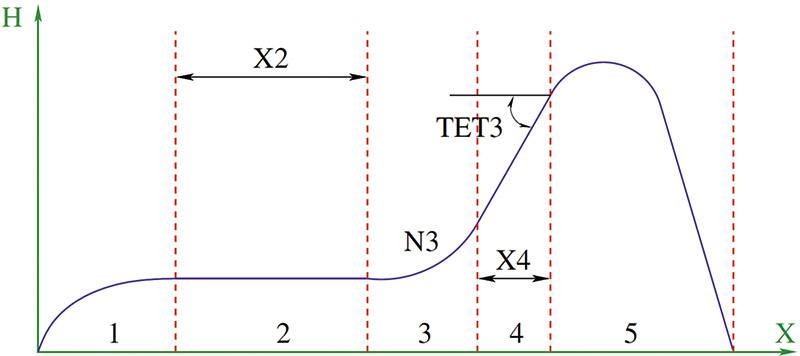
Рис. 1. Параметрическое представление траектории

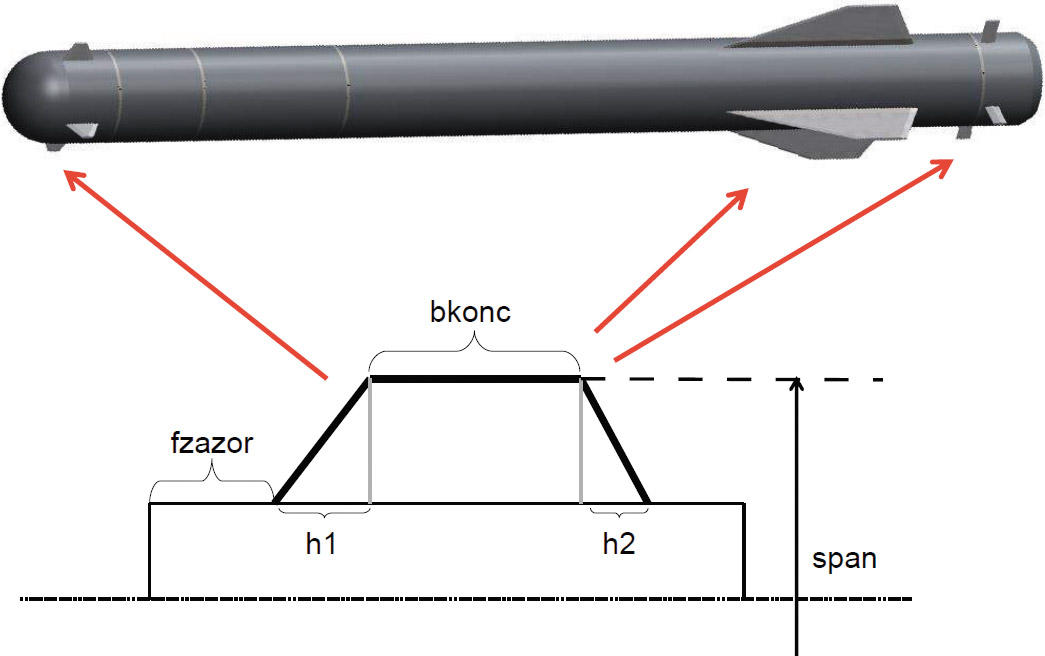
Рис. 2. Параметризованная геометрия рулевых элементов

В сделанных предположениях критерием качества решения является время подлета T к цели, расположенной на заданном расстоянии от точки пуска (чем меньше потребное время, тем лучше).

В рассмотренной задаче общегеометрические параметры изделия (калибр и длина) считались заданными и неизменными. В этих условиях количественное определение понятия «аэродинамическая компоновка» сводится к геометрии и расположению вдоль корпуса дестабилизаторов, крыльев и рулей (рис. 2), количество которых считалось фиксированным (по четыре элемента каждого типа, расположенных на одной линии вдоль оси изделия). При этом геометрия и положение каждого элемента задается пятью параметрами:

• ?fzazor — смещение элемента в соответствующем сегменте изделия;
• ?h1, h2 — определяют стреловидность элемента;
• ?bkonc — длина боковой хорды;
• ?span — размах соответствующего элемента.

Таким образом, в рассматриваемой задаче аэродинамическая компоновка определяется 15 (5·3) параметрами, изменяемыми в заранее заданных диапазонах, которые, в свою очередь, диктуются размерами отсеков и максимально технологически допустимыми удлинениями.

Переменные оптимизации не исчерпываются геометрией рулевых элементов — для достижения минимального времени подлета к цели позволяется также изменять законы управления, а следовательно, и форму траектории. Закон управления параметризован четырьмя величинами (см. рис. 1):

• ?X2 — длина горизонтального участка траектории (участок 2);
• ?N3 — величина перегрузки при выходе на «горку» (участок 3), которая принимается постоянной на всем участке;
• ?TET3 — угол наклона траектории к горизонту на участке 4 прямолинейного набора высоты;
• ?X4 — длина участка 4 траектории.

Все параметры управления также изменяются в заранее заданных диапазонах.

Остальные ограничения задачи подразделяются на два типа: дополнительные ограничения на геометрию рулевых элементов, не сводящиеся к простым диапазонам изменения параметров, и ограничения на траекторию полета. Смысл первой группы ограничений прост: размеры дестабилизаторов, крыльев и рулей не должны превышать размеров соответствующих отсеков (три линейных ограничения); в каждом элементе аэродинамического управления допустимые углы схождения передней и задней кромок ограничены (шесть нелинейных ограничений); кроме того, для крыльев требуется, чтобы размер бортовой хорды был не меньше заданного (одно линейное ограничение).

Что касается траектории полета, то ее допустимость характеризуется следующими величинами (их вычисление обсуждается ниже):

•  полная горизонтальная длина траектории X (расстояние до цели), с учетом начального 1 и терминального 5 участков (см. рис. 1), лежит в заданном интервале;
•  захват цели (горизонтальная длина X5 участка 5) происходит на расстояниях не меньше заданного;
•  располагаемая перегрузка в конце траектории должна быть достаточно большой;
•  частоты реагирования не становятся слишком малыми;
• угол подлета к цели (по отношению к вертикали) достаточно мал.

Таким образом, в рассматриваемом приближении задача поиска оптимальной аэродинамической компоновки ПТУР сводится к однокритериальной оптимизационной задаче следующего вида:

                                 (1)

где ,  обозначает множество оптимизируемых переменных и диапазоны их изменения, линейные ограничения выделены явно, а  обозначает множество ограничений общего вида.

Для полного определения задачи остается сформулировать способ вычисления нелинейных характеристик, составляющих ограничения общего вида .
В общем случае расчет этих величин требует рассмотрения нескольких дисциплин (внешняя аэродинамика, баллистика), для которых возможно использование различных физических моделей и соответствующих программных модулей. Обстоятельством, серьезно упрощающим решение задачи, явилось наличие адекватных валидированных расчетных программ на предприятии, что автоматически сняло вопросы о степени адекватности использованных моделей. С практической точки зрения, при решении задачи использовалось два расчетных модуля, разработанных специалистами КБП, и стандартная функциональность CAD­системы NX. Краткое описание функциональности каждого компонента удобно привести одновременно с описанием всей расчетной цепочки, реализованной в интеграционной платформе pSeven (рис. 3). Отметим, что каждый представленный на рисунке блок представляет собой логически замкнутый функциональный элемент расчетной схемы, стрелки обозначают направление потока данных. Таким образом, pSeven позволяет собрать всю расчетную цепочку средствами визуального программирования, при этом собранная расчетная схема также представляет собой функциональный блок с однозначно определенными форматами входных/выходных данных и может быть использована в дальнейшем для построения более сложных схем.

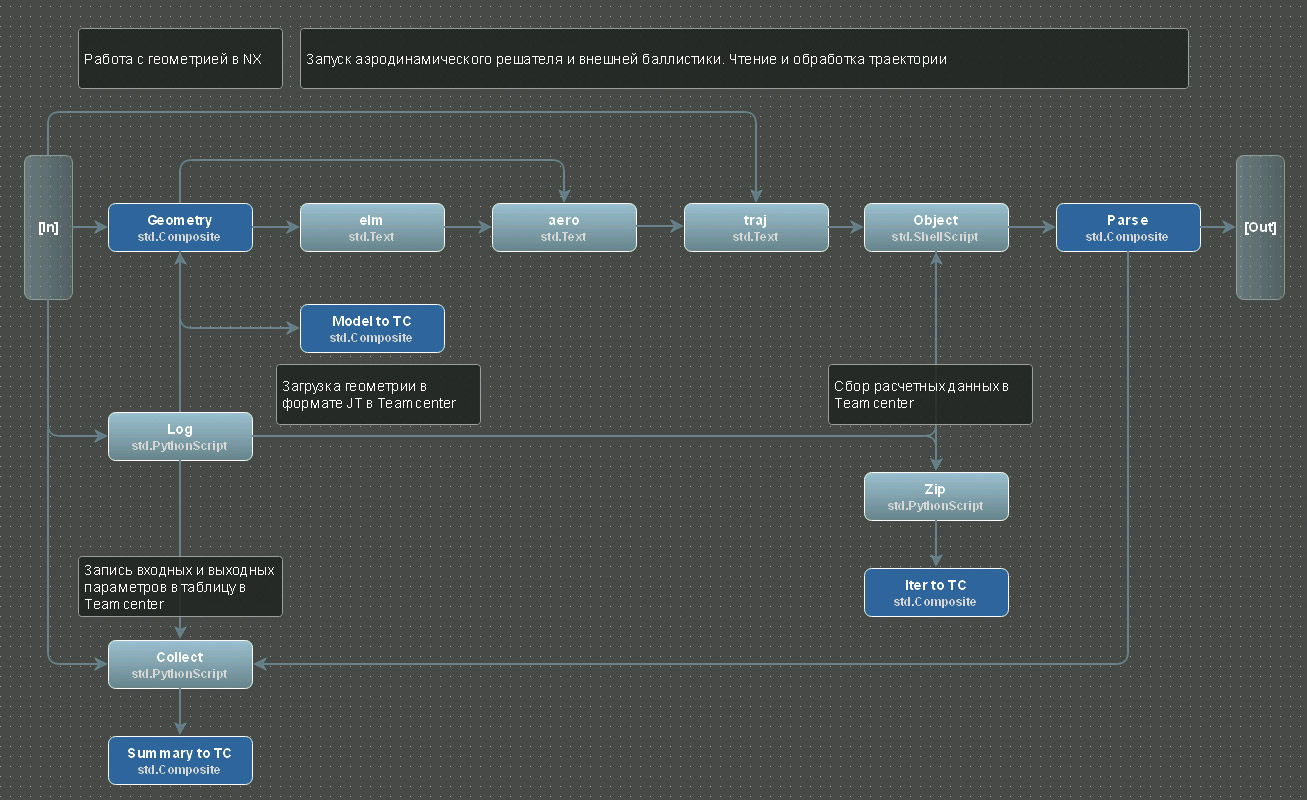
Рис. 3. Расчетная последовательность для вычисления нелинейных характеристик, представленная в виде вычислительной цепочки pSeven

Расчетная последовательность , требуемая уравнением (1) и изображенная на рис. 3, устроена следующим образом:

• входные данные, поступившие на вход расчетной цепочки, разбиваются на параметры геометрии и управления. Геометрические параметры поступают в блок Geometry, функционально представляющий собой CAD NX [3] и выполняющий расчет масс­инерционных характеристик (МИХ) изделия. Отметим, что все продукты линейки NX имеют прямую интеграцию с PLM­системой Teamcenter. Блоки Log, Collect, Summary to TC, Model to TC являются вспомогательными и позволяют сохранить полную информацию об инициализированном расчете в TC, взаимодействие с которым описывается в следующем разделе;
• вычисленные МИХ позволяют посчитать аэродинамические параметры изделия, что происходит в блоке aero (после преобразования данных в соответствующий формат в блоке elm). Функционально блок aero представляет собой отдельное приложение, разработанное специалистами КБП и осуществляющее расчет аэродинамических характеристик изделия по линейной модели (см., например, [4]). Отметим, что несмотря на относительную простоту модели, аэродинамический расчет для рассматриваемого класса изделий является верифицированным в широкой области скоростей (числа Маха от 0 до 7) и высот (от 0 до 80 км) полета;
• вычисленные аэродинамические данные об изделии и заданные параметры управления позволяют полностью восстановить траекторию в блоке traj, который функционально представляет собой отдельное приложение. Отметим, что форма начального участка траектории является фактически фиксированной, в то время как терминальный участок выводится из закона пропорционального сближения;
• на последней стадии расчета полученная траектория анализируется в блоке Object (отдельное приложение, разработанное специалистами КБП), в котором вычисляются оставшиеся величины (конечная располагаемая перегрузка, частоты реагирования). На этом этапе также используются вспомогательные блоки Zip, Inter to TC, Parse для записи полученных характеристик в PLM TC.

Отметим, что для простоты изложения мы не рассматривали вопросы корректной обработки ошибок в работе различных блоков, в большинстве случаев они легко решаются стандартными средствами pSeven.

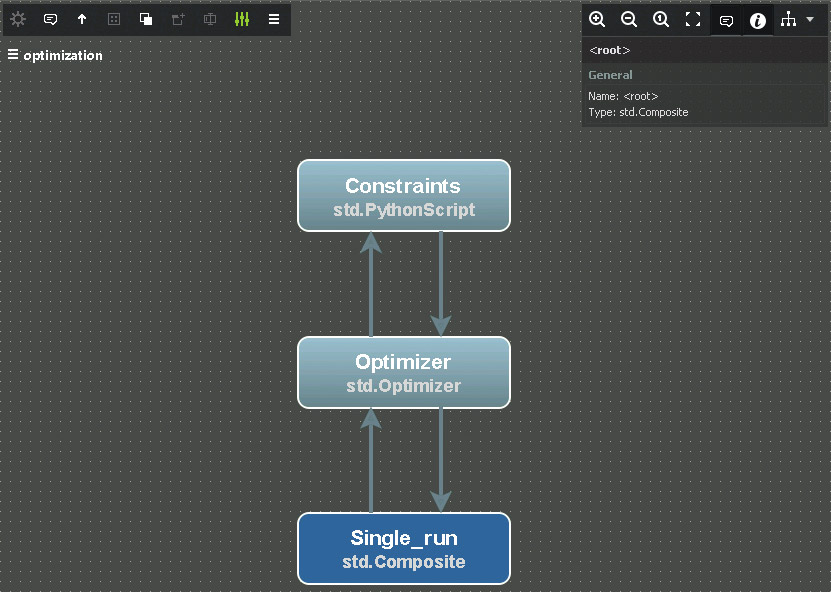
Рис. 4. Схема решения оптимизационной задачи в pSeven

Собранная и отлаженная расчетная последовательность позволяет непосредственно перейти к решению задачи (1). Единственная тонкость заключается в том, что линейные ограничения задачи желательно задать отдельным образом. Дело в том, что подавляющее большинство оптимизационных методов (методы pSeven не являются исключением) по­разному работают с линейными и нелинейными данными; явное разделение этих двух типов обычно существенно повышает эффективность нахождения решения. Окончательная расчетная схема для решения задачи (1) в pSeven представлена на рис. 4, где блоки представляют собой:

• ?Single_run — описанная выше расченая схема вычислений нелинейных характеристик (рис. 3), представленная в виде единого составного блока pSeven;
• ?Constraints — вычисление линейных ограничений задачи;
• ?Optimizer — стандартный блок pSeven, предоставляющий множество оптимизационных алгоритмов и собственно решающий задачу (1).

Интеграция с Teamcenter

Teamcenter [5] является системой управления жизненным циклом изделия и имеет модульную структуру. Хранимые данные имеют связи между собой, которые описываются моделью данных. Такой подход обеспечивает целостность данных, поддерживает версионность и разграничение доступа.

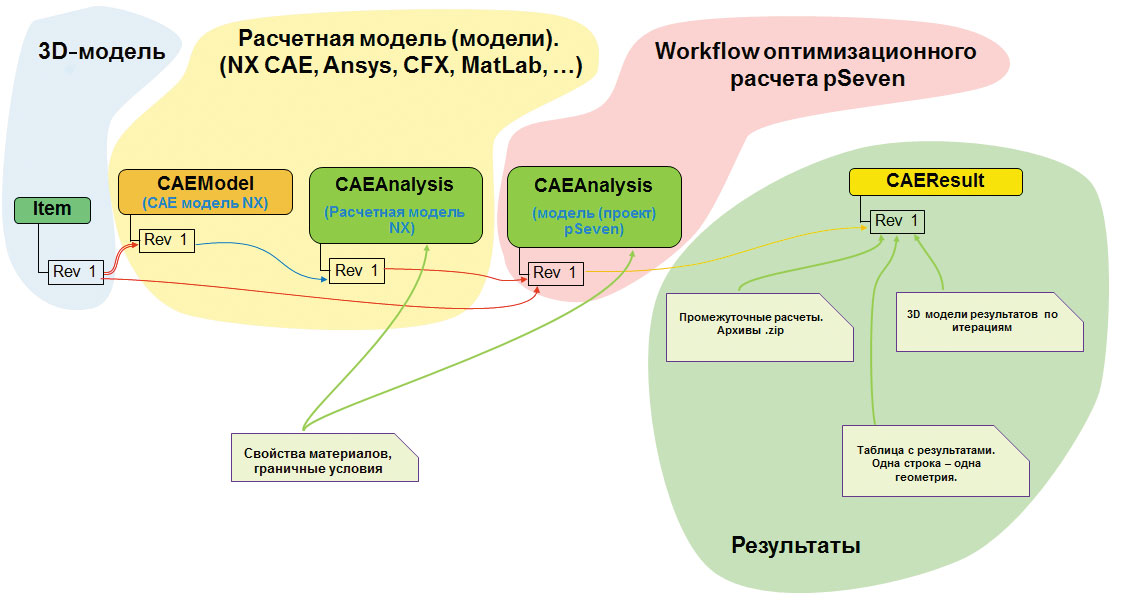
Рис. 5. Модель данных оптимизационного расчета в среде Teamcenter

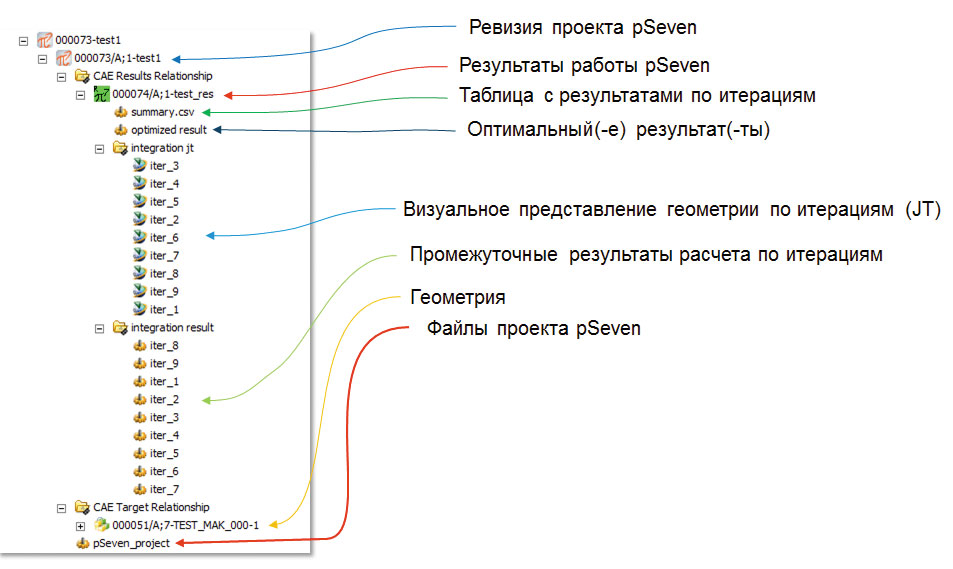
Рис. 6. Графическое представление модели данных оптимизационного расчета в среде Teamcenter

Модель данных — это описание шаблона структуры взаимосвязи компонентов между собой. Например, в модель данных оптимизационного расчета (рис. 5 и 6) может быть добавлен блок «Расчетная модель», в котором хранятся все расчетные модели, участвующие в оптимизации. И хотя в данной работе такой блок не применялся, возможность сохранения моделей является важной и удобной отличительной особенностью Teamcenter. Наборы данных (например, свойства материалов и граничные условия) также имеют механизм версионирования.

Проведение оптимизационного расчета в среде Teamcenter выглядит следующим образом:

1. Необходимая ревизия элемента в Teamcenter открывается для редактирования.
2. Указывается папка на файловой системе, куда автоматически импортируются все необходимые для расчета файлы. Также автоматически создается двухсторонняя связь папки с Teamcenter, при этом ревизия 3D­модели в Teamcenter автоматически блокируется от изменений.
3. Дальнейшая работа с проектом производится точно так же, как если бы никакой связи с Teamcenter не было (сам Teamcenter может быть закрыт), — производится оптимизационный расчет, вносятся изменения в постановку задачи и т.п.
4. Teamcenter сохраняет сделанные в проекте изменения по требованию пользователя, при этом структура данных автоматически обновляется из связанной папки на файловой системе (из папки проекта).

Запуск оптимизационного расчета происходит непосредственно в pSeven и не отличается от обычного запуска. При этом во время расчета происходит автоматическая передача результатов по итерациям в Teamcenter. Таким образом, ведущий специалист может просматривать результаты проводимых расчетов фактически в режиме реального времени, при этом никакого дополнительного взаимодействия с pSeven не происходит.

На рис. 7 приведен пример отображения результатов оптимизационного расчета в среде Teamcenter, где по горизонтали отложен индекс рассчитанной модели ПТУР с измененными геометрическими параметрами, а по вертикали изображены расчетные характеристики соответствующего варианта изделия. Отметим, что все графики интерактивны и могут быть настроены по количеству выводимых параметров, масштабу и способу отображения.

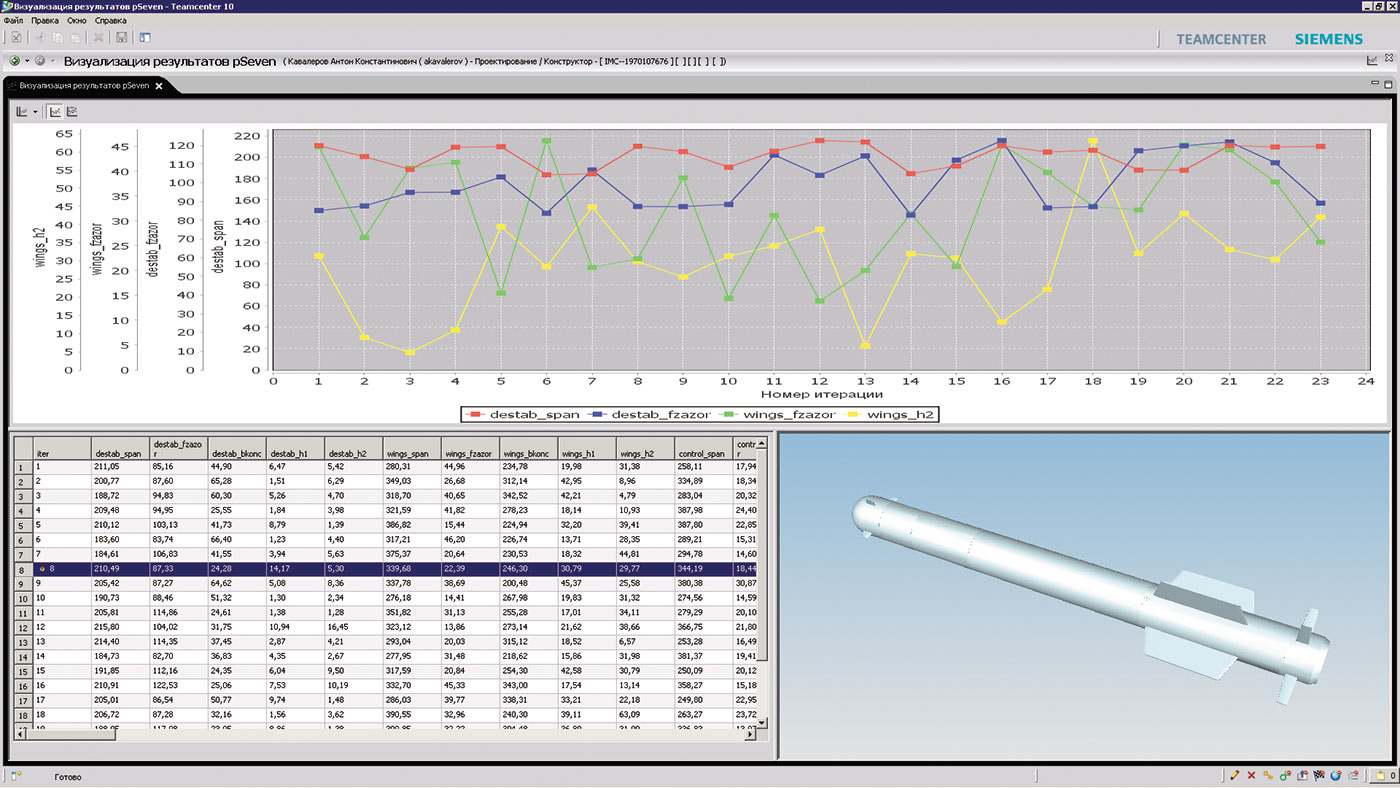
Рис. 7. Представление данных оптимизационного расчета в среде Teamcenter

Результаты

Задача нахождения оптимальной аэродинамической компоновки ПТУР была решена с помощью интеграционной платформы pSeven, дополненной необходимой функциональностью PLM Teamcenter. Такой подход автоматически разрешает большую часть технических вопросов, в том числе и вопросы выбора эффективных оптимизационных алгоритмов. Тем не менее тип проводимой оптимизации с необходимостью должен быть выбран на этапе постановки задачи:

• оптимизация может быть нацелена на улучшение характеристик уже существующего изделия, и тогда имеет смысл говорить о локальной оптимизации, которая призвана найти оптимальное решение с высокой точностью, но в окрестности известного решения;
• либо же речь идет об обликовых исследованиях, в которых точность нахождения решения может быть невелика, но требуется провести поиск решений во всем пространстве параметров.

Рассматриваемая задача безусловно принадлежит второму классу, выбор подходящих алгоритмов оптимизации не составляет труда: наиболее эффективными алгоритмами в данном контексте являются методы на основе метамоделирования. Поставленная задача была решена методами именно этого семейства; в данной работе мы не будем останавливаться на подробностях соответствующих алгоритмов, тем более что pSeven предоставляет необходимую функциональность автоматически. Достаточно сказать, что результаты, представленные ниже, были получены всего за 280 обращений к расчетным модулям, что является исключительно малым числом для задачи с 19 оптимизируемыми параметрами.

Особенностью оптимизационного модуля pSeven является то, что при решении любой задачи ответ представляет собой не только найденное лучшее решение, но и множество других кандидатов, которые, проигрывая по формальным критериям, тем не менее, представляют отдельный интерес, так как при сравнимом качестве сильно отличаются от лучшего решения в пространстве оптимизируемых переменных. Именно эта особенность позволила сравнительно быстро идентифицировать фактически только два решения задачи, представленных на рис. 8. Отличительной чертой найденных решений является то, что при несущественном отличии времен подлета (32,74 [34,78] секунды для конфигурации, представленной слева [справа] на рис. 8), геометрии найденных решений существенно различны. Сравнительный вид траекторий полета приведен на рис. 9.

Рис. 8. Два лучших решения задачи поиска оптимальной аэродинамической компоновки ПТУР
(формально лучшее решение расположено слева)

Таким образом, можно сделать вывод, что существует несколько различных компоновок, обладающих примерно одинаковым характеристиками (время и угол подлета к цели, располагаемая перегрузка и др.). Более того, расчеты показывают, что характеристики траекторий для двух существенно различных обликов изделия близки1 . Следовательно, несмотря на различие геометрий, решения обладают некоторыми общими свойствами. Рассмотрение диаграммы параллельных координат, представленной на рис. 10, позволяет сделать вывод, что искомая оптимальная компоновка:

• имеет крыло большого размаха с большой концевой хордой;
• имеет развитый трапециевидный руль большого размаха;
• может не иметь дестабилизатора (по крайней мере, его влияние достаточно мало);
• закон управления имеет следующую структуру:

- участок 3 должен поднимать изделие на угол 18­23°;

- длина участка 4 составляет 1700­1800 м.

Заключение и выводы

При решении задачи поиска оптимальной аэродинамической компоновки ПТУР было показано, что интегрированное решение для оптимального проектирования в управляемой среде на базе pSeven и Teamcenter позволяет:

• улучшить технические и эксплуатационные характеристики изделия;
• упростить процесс принятия конструкторских решений;
• сравнительно легко объединить множество дисциплин в рамках одного процесса и таким образом вывести исследования на качественно новый многодисциплинарный уровень.

Важно отметить, что использование связки pSeven+Teamcenter дает возможность избежать многих проблем, которые обычно возникают при внедрении процессов автоматизированного проектирования на крупных предприятиях. Например, было показано, что удается не только автоматизировать инженерные расчеты, необходимые для синтеза облика сложных технических изделий, но и одновременно с тем контролировать целостность информации и обеспечить привязку требований на изделие к проводимым расчетам. Кроме того, в рамках использованного подхода легко удается формализовать взаимодействие между подразделениями, сохранять все проведенные расчеты в единой среде и таким образом отслеживать, на основе каких расчетов приняты те или иные конструкторские решения. Таким образом, интеграция pSeven + Teamcenter + NX существенно упрощает построение и внедрение процессов оптимального проектирования и обеспечивает уверенное преимущество в достижении поставленных целей. 

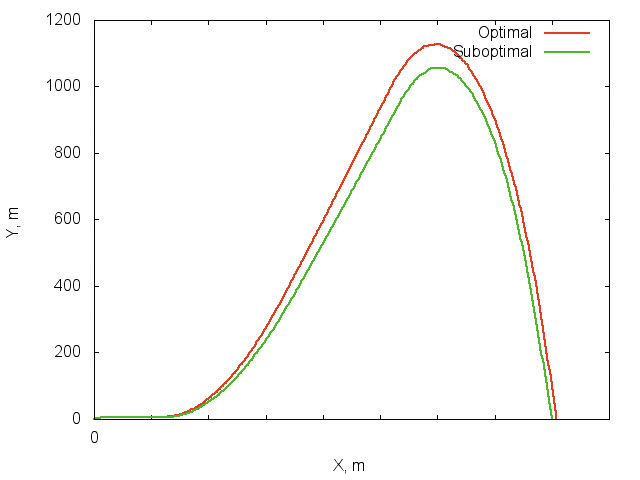
Рис. 9. Сравнение траекторий двух лучших решений

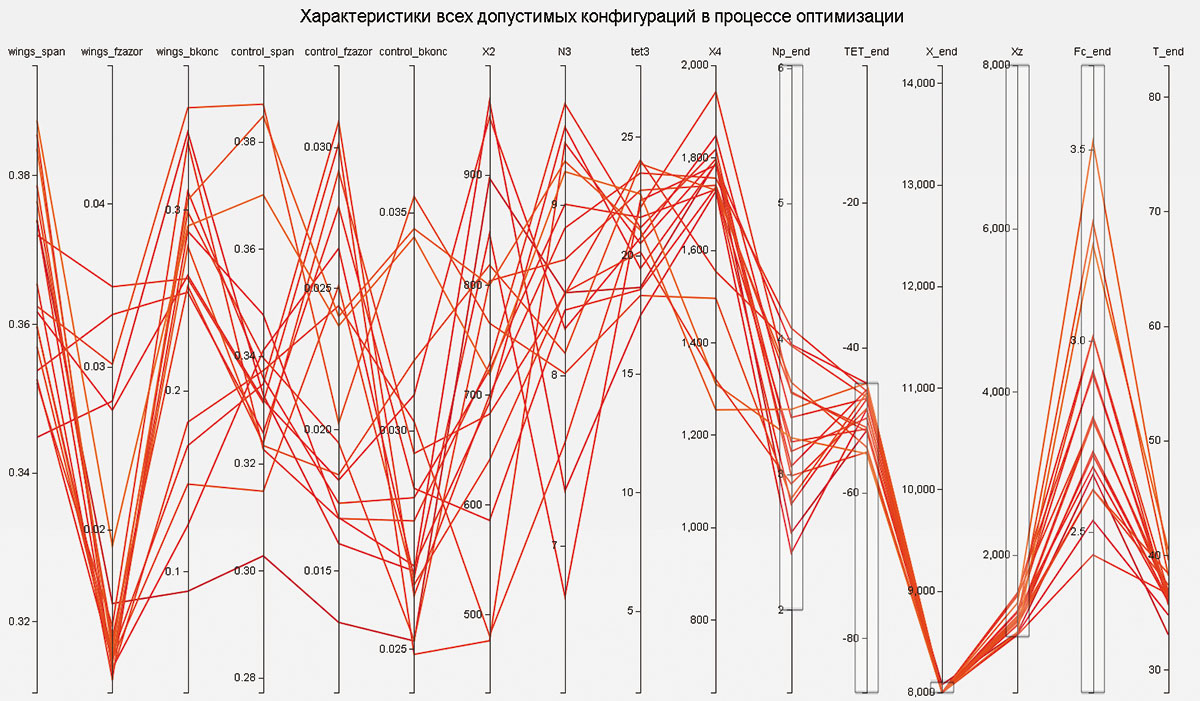
Рис. 10. Характеристики всех допустимых конфигураций, найденных в процессе решения

Ссылки:

1. http://www.datadvance.net.
2. http://www.borlas.ru.
3. Документация по NX 10: https://docs.plm.automation.siemens.com/tdoc/nx/10.0.2/nx_help/#uid:index.
4. Лебедев А.А., Чернобровкин Л.С. Динамика полета беспилотных летательных аппаратов. Машиностроение, 1973.
5. Документация Teamcenter 10.1.3: https://support.industrysoftware.automation.siemens.com/docs/teamcenter/10.1.3/help/#uid:index.

САПР и графика 7`2016