Оптимизация вычислений в C3D Toolkit и новые возможности расширенного формата C3D для чтения и записи геометрии

Александр Спиваков, Татьяна Митина

Многие специалисты изо дня в день используют функционал трехмерного моделирования в системах автоматизированного проектирования, но далеко не каждый конструктор или проектировщик задумывается о том, что же кроется за ширмой привычных интерфейсных команд, обеспечивающих столь ценимый комфорт и удобство проектирования изделий в 3D. Как правило, на общее впечатление от использования САПР влияет быстродействие при работе с большими сборками, а также скорость загрузки 3D-моделей в систему. В инженерном сообществе вполне справедливо и небезосновательно считается, что за эту часть функционирования отвечает геометрическое ядро. Компания C3D Labs, дочернее предприятие группы АСКОН и резидент ИТ-кластера «Сколково», с 2012 года занимается созданием коммерческого ядра C3D Modeler. В данной статье наши сотрудники Александр Спиваков и Татьяна Митина постараются объяснить, из чего на практике складывается повышение производительности в ключевых компонентах САПР.

Александр Спиваков, руководитель группы C3D Converter и ведущий разработчик C3D Modeler для Teigha

При постановке и решении задачи по оптимизации программного кода под многоядерную архитектуру не всегда очевидна сложность работ, с которыми сталкиваются разработчики программного обеспечения. Ускорение вычислений за счет многопоточности в области САПР вообще представляет собой нетривиальную задачу. И чтобы объяснить это, мы начнем издалека, а именно с математической модели объектов трехмерного мира.

Математическая модель физических тел

Большинство ядер CAD­систем оперируют граничным представлением геометрии. В переводе на человеческий язык это означает следующее: пространство делится на две части — заполненную материалом и всё остальное. Граница этих двух частей представляет собой стыкующиеся кусочки разных поверхностей так, чтобы между ними не было щелей. То, как именно стыкуются кусочки и какая часть заполнена материалом, — называется «топологией», которая не очень хорошо подходит для иллюстрации многопоточности. А вот описание поверхности… Штука, вроде, простая, пока не вступает в свои права вычислительная математика. Берется декартова система координат, и в ней задаются функции радиус­вектора (x, y, z) в параметрической области (u, v). В формулах x, y, z, u, v — это числа с плавающей точкой. Для указания, какой кусочек поверхности брать, используются кривые. С ними уже разнообразнее: кривые могут быть определены как в области определения поверхности u(t), v(t), так и в трехмерном пространстве (x, y, z). Здесь t — тоже число с плавающей точкой, которое называется «параметром кривой». Собственно, на кривых мы и проиллюстрируем некоторые трудности, которые возникают, стоит только заняться написанием программного кода.

Перевод формул в числа

Вычислительная математика — это страна чудес, где, например, сумма меняется от перестановки слагаемых. Но это довольно тонкие эффекты, к которым порой приходишь через гораздо более насущные задачи, а именно — поиск способов подсчета радиус­вектора (u, v) при произвольных допустимых значениях параметра t. Способов много: аналитические или специальные функции для каждой координаты, различные сплайны и т.д. Во всех способах есть ухищрения, которые позволяют уменьшить потребное число арифметических операций, и за каждый из этих способов приходится платить свою цену: или операций будет слишком много, или придется заниматься поиском, или и то и другое вместе. Причем, речь идет именно об арифметических операциях, потому что большинство способов изобреталось в эпоху, когда в ходу были таблицы Брадиса, логарифмические линейки и механические арифмометры. Стоит ли говорить, что каждый знак после запятой нужно было обосновывать (о, да, неустойчивость алгоритмов!), потому как они переводились в человеко­часы? Нужно его обосновывать и теперь, потому что прогресс вычислительной техники позволил расширить круг решаемых задач и ряд задач, которые некогда считались суперсложными, перешли в разряд даже не рутинных, а вспомогательных. Соответственно, требования к точности и быстродействию не стали менее актуальными. Точность недостаточна — результат будет практически неприменим. Точность избыточна — результат успеет устареть прежде, чем будет получен.

Что такое кэширование, и что оно дает

Задача оптимизации вычислительного алгоритма формулируется так: сократить количество необходимых операций, поскольку оно определяет время вычислений. Для многих задач уже сформулированы эффективные вычислительные алгоритмы. Тем не менее для прикладных задач наибольшую ценность представляют не те алгоритмы, которые входят в библиотеки, а реализованные самостоятельно, с учетом специфики применения.

Практика показывает, что зачастую набор значений параметра, для которых вычисляется радиус­вектор, подчиняется некой закономерности или статистике. Именно на предположении о том, что значения параметра не являются произвольными, основан такой метод оптимизации, как кэширование данных.

Под кэшированием понимается сохранение неких промежуточных или конечных результатов, которые могут быть использованы повторно с целью сокращения объема последующих вычислений. Область оперативной памяти, в которой хранятся те данные, которые предполагается использовать, называется кэшем; также под кэшем может пониматься сам набор данных.

Платой за использование этого способа оптимизации (кэширование) является дополнительный расход памяти, так как рассчитанные значения и параметры надо где­то хранить. Как показывает практика, явный учет частных случаев встречается достаточно часто, чтобы быть реализованным для получения выигрыша во времени.

Следующий пример иллюстрирует, как работает кэширование.

Затраты на вычисление

Рассмотрим самое прекрасное, что есть в двумерии, согласно Пифагору, — это окружность. u(t) = cos(t), v(t) = sin(t) — единичный радиус, начало координат. «Загоняем» параметр t в диапазон от 0 до 2π. Далее могут быть варианты, например можно использовать формулы приведения (навешивать на синус и косинус знаки плюс и минус в зависимости от «обстоятельств»), а считать синус­косинус в диапазоне вчетверо более коротком — до π/2.

Теоремой Пифагора пользоваться не будем, потому что всё равно придется расписывать ряд Тейлора, но уже для квадратного корня. Можно работать итерационным методом.

Перейдем к численным оценкам. Посчитаем, сколько потребуется выполнить арифметических операций, чтобы вычислить синус угла с заданной точностью, используя ряд Тэйлора. В качестве примера возьмем угол 30°: для получения точного значения ½ до 15­го знака (с машинной точностью) необходимо просуммировать семь членов ряда:

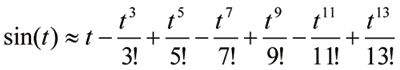
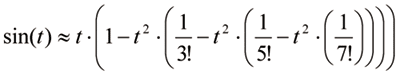
Четыре члена ряда дают «мусор» в восьмом знаке, три члена — в шестом. Это соответствует максимальной степени, в которую возводится параметр: 13, 7 и 5 соответственно. Если считать по схеме Горнера и явно использовать тот факт, что суммируются только нечетные степени, то для суммирования многочлена 7­й степени потребуется восемь операций:

И так каждый раз? В общем случае — да. А в частном? Это зависит от конкретного случая.

Например, если нужно посчитать значения при двух близких значениях параметра, можно укоротить ряд Тейлора. Насколько близких и насколько укоротить — это зависит от требуемой точности. Допустим, нас устраивает точность до восьмого знака. Для вычисления значения косинуса с такой точностью потребуется суммировать ряд до 8­й степени. Оценки показывают, что для разницы углов π/50 (со знаком как плюс, так и минус) ряд Тейлора для синуса и косинуса можно укоротить до 3­й и 4­й степеней соответственно. А потом используются формулы для вычисления синуса и косинуса суммы углов:

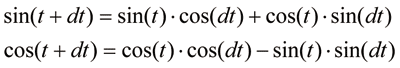
В этом примере хорошо видно, почему имеет смысл считать синус и косинус, а не пользоваться теоремой Пифагора: можно сохранить в кэше предыдущее значение параметра и значения синуса и косинуса угла, которые ему соответствуют. Шесть операций на вычисления по формулам плюс восемь операций для вычисления ряда — итого 14 против 16. Совсем небольшой выигрыш для каждой последующей близкой точки, сокращение затрат от силы на 10%. Если бы не одно важное обстоятельство (рис. 1).

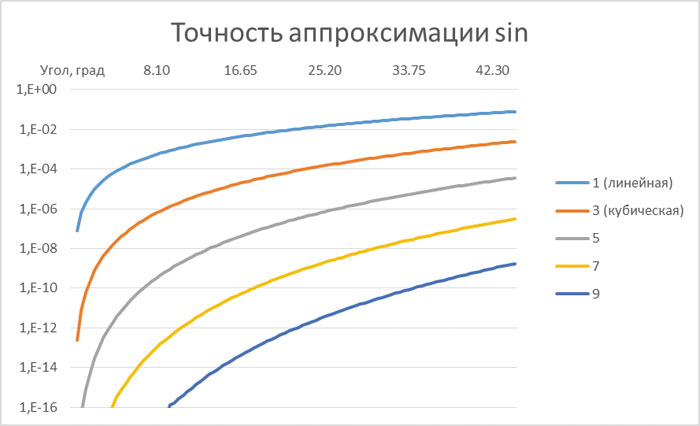
Рис. 1. Точность аппроксимации функции многочленами разной степени

Оценка трудоемкости точного расчета была сделана так, словно заранее известно, сколько членов ряда нужно суммировать. Но в реальности, чтобы узнать, сколько членов ряда нужно суммировать, следует вычислять каждый член ряда по отдельности и сравнивать его со значением точности, чтобы по достижении порога завершить расчет. Затраты на вычисление всех членов ряда примерно соответствуют вычислению суммы с использованием схемы Горнера, при этом члены ряда еще нужно просуммировать. В зависимости от величины угла необходимое число членов ряда, которое определяет число операций, может варьироваться в ту или иную сторону. В рассматриваемом примере вместо 16 следует писать 24. То есть выигрыш становится порядка 40%: 14 против 24. Это уже кое­что!

Понятно, что кэш сплайна будет отличаться от кэша дуги, что кэш поверхностей будет устроен иначе. Важен сам принцип.

Программная надстройка над аппаратным базисом

С тех пор, как многоядерные процессоры стали не просто доступны, а начали восприниматься как нечто само собой разумеющееся, всё более актуальной стала задача написания такого кода, который задействовал бы аппаратные средства максимально эффективно. Ускорение может быть достигнуто за счет одновременного выполнения различных расчетов на разных процессорах или ядрах.

Само по себе наличие нескольких ядер не обеспечивает ускорения вычислений, а только предоставляет для этого некоторую аппаратную возможность. Многопоточность — это всего лишь один из способов задействовать имеющиеся возможности. Потоки — это объекты ядра операционной системы, которые могут очень эффективно взаимодействовать между собой, применяя, грубо говоря, оперативную память. В идеале для корректной работы потоков нужно, чтобы они не использовали одни и те же участки памяти. В случае геометрического ядра — одни и те же кэши. К сожалению, граничное представление геометрической модели так устроено, что для подавляющего большинства операций подобное разделение не гарантируется, если всё оставить в таком виде, как это было в эпоху одноядерных процессоров.

Поэтому, оптимизируя алгоритмы для многопоточной среды, не следует полагаться на одно только ускорение, которое достигается за счет использования многоядерности. Во­первых, потому что не все задачи хорошо распараллеливаются. Во­вторых, следует учитывать, что потоками и аппаратными ресурсами, например ядрами, управляет не прикладная программа и не геометрическое ядро, а операционная система. Сам тот факт, что работа программы зависит не только от труда ее автора, указывает на необходимость оптимизации кода, который исполняется внутри потока. В некотором смысле давно разработанные и оптимизированные «однопоточные» алгоритмы являются эталоном быстродействия для своих «многопоточных» модификаций (рис. 2).

Рис. 2. Пример алгоритма, оптимально подходящего для распараллеливания (каждая проекция считается в отдельном потоке)

Пока не встал вопрос о многопоточности, пожалуй, единственным фактором, который ограничивал использование кэшей, был объем доступной оперативной памяти. Требование работы в многопоточной среде привело к ревизии архитектуры программных комплексов и практической реализации вычислительных алгоритмов.

Собственно, обеспечение работоспособности в многопоточной среде при сохранении эффективности «однопоточной» реализации и является одним из ноу­хау C3D Labs. При развитии в этом направлении приходится модифицировать архитектуру системы так, чтобы выполнялся ряд условий:

1. Обеспечивалась максимальная эффективность от использования многопоточности.
2. Сохранялась эффективность в однопоточном варианте.
3. Обеспечивалась максимальная совместимость кода.
4. Условия пп. 1­3 распространялись на максимально возможное число операций.

Решение первой задачи, по сути, означает поиск компромисса между безопасностью и эффективностью. Любые проверки стоят байтов памяти и тактов процессорного времени. Это сложная и интересная работа, которая уже принесла первые результаты (рис. 3).

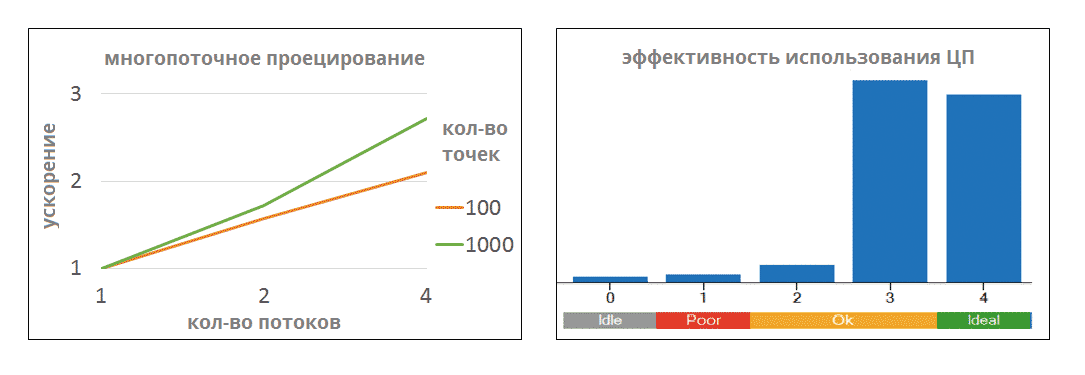
Рис. 3. Результат оптимизации кода в C3D Modeler 2016 при проецировании 100 и 1000 точек на произвольную NURBS-поверхность

Есть и другие условия, например требование кроссплатформенности. Оно налагает ограничение на используемые технические средства. Применение технологии OpenMP для оптимизации кода геометрического ядра C3D Modeler позволило нам одновременно решить проблемы кроссплатформенности и совместимости.

Большинство пользователей САПР при работе с большими и сложными 3D­моделями сталкиваются с одной и той же проблемой: геометрические модели достаточно долго загружаются в систему, поэтому неизбежно приходится ждать какое­то время, прежде чем можно будет продолжить работу по проектированию изделия. Добавим к этому необходимость повторять процедуру каждое утро перед началом рабочего дня, и вот мы получаем мелкий, но назойливый раздражитель, а вместе с ним и недовольство пользователей САПР.

Татьяна Митина, руководитель отдела программирования в нижегородском офисе C3D Labs

В сложившейся ситуации разработчики систем автоматизированного проектирования стремятся всячески улучшить показатели загрузки. В частности, в машиностроительной САПР КОМПАС­3D предусмотрено несколько вариантов загрузки информации из файла: модель с историей построения, фасетная модель и габаритный ящик. Пользователь сам выбирает, что ему нужно, и, таким образом, задача решается на уровне приложения.

Есть и другие примеры. Так, разработчики формата JT при проектировании архитектуры решили запечатлеть в файле сразу два представления геометрии: граничное и полигональное. Это сделано для того, чтобы при первоначальной загрузке данных в приложение подгружалось фасетное представление модели (которое сразу может быть передано на отрисовку), а параллельно, если потребуется, загружалось более «тяжелое» граничное представление, над которым производится большая часть пользовательских манипуляций в САПР. Формат JT является открытым, вследствие чего применить его можно не только в системах проектирования, но также в простых просмотрщиках моделей и в более сложных программах для работы с метаданными.

Из всего вышесказанного можно сделать вывод, что оптимизация работы с файлом является востребованной задачей как на уровне конечного приложения, так и на более низком уровне. Поэтому в C3D Labs мы озаботились вопросами повышения производительности при работе с форматом C3D, который является родным для геометрического ядра C3D Modeler. В результате был разработан и реализован расширенный формат хранения геометрической модели, поддерживающий чтение из файла отдельных объектов модели в произвольном порядке и позволяющий получить информацию о структуре модели и ее объектах без загрузки всей модели из файла. Теперь рассмотрим работу с форматом C3D более подробно.

Стандартный формат C3D

Стандартный формат C3D обеспечивает компактную и быструю запись геометрической модели в файл. Он позволяет записывать объекты модели последовательно в единое пространство файла, которое представляет собой набор блоков (кластеров) и имеет единственную точку записи в текущем кластере. При заполнении текущего кластера выделяется новый, и точка записи перемещается в него.

Когда геометрический объект ссылается на другой объект, внутренний объект записывается внутри ссылающегося на него объекта. При этом объект модели, на который ссылаются несколько других объектов, записывается внутри первого ссылающегося объекта и регистрируется в таблице «Регистрируемые объекты». Все последующие объекты, ссылающиеся на данный объект, содержат индекс из таблицы объектов (рис. 4).

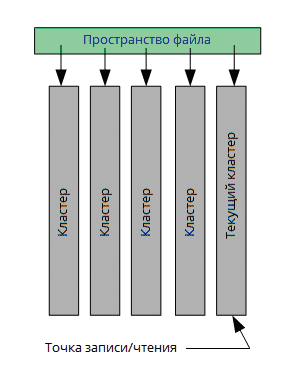
Рис. 4. Хранение объектов геометрической модели в стандартном формате C3D

Преимущества такого классического подхода — это минимум накладных расходов при записи файла, компактность формируемого файла, простота программной реализации и удобство использования API. В то же время такая организация работы с данными налагает ограничения на использование формата C3D:

• информация о структуре модели или отдельных ее объектах может быть получена только после прочтения всей модель целиком;
• загрузка объектов модели в произвольном порядке и импорт отдельных объектов невозможны, так как: а) информация о позиции хранения объекта в файле C3D отсутствует; б) объект может быть вложен в другой объект или ссылаться на такой объект, для которого неизвестна позиция хранения.

Чтобы уйти от подобных ограничений, как раз и был разработан расширенный формат C3D.

Расширенный формат C3D

Обновление формата C3D потребовало от команды C3D Labs детальной проработки основных требований к новой структуре формата. Отчасти они уже были сформулированы ранее — это обеспечение независимого хранения объектов и возможность их выборочного чтения, а также предоставление доступа к информации об объектах геометрической модели без чтения всей модели из файла. Среди дополнительных требований стоит отметить создание новых интерфейсов (для чтения и записи моделей, объектов и пр.) и, что немаловажно, поддержку совместимости с текущим форматом C3D.

Уже на стадии реализации потребовалось решить, куда записывать информацию о выстроенной иерархии модели, характеристики объектов и позиции их хранения. В итоге был разработан механизм создания и хранения оглавления в файле модели и реализована однопроходная обработка геометрической модели при записи в файл, при которой одновременно записывается модель и формируется ее оглавление (дерево модели).

Само оглавление объектов геометрической модели в расширенном формате содержит не только сведения об иерархии, но и информацию о всех ее объектах, поддерживающих журнал построения и атрибуты (проволочный каркас, точечный каркас, твердое тело и другие объекты типа Item). Для каждого объекта хранятся следующие характеристики:

• тип объекта;
• имя объекта;
• габарит объекта и локальная система координат (если она имеется);
• позиция записи/чтения объекта в файле.

Кроме того, есть возможность дополнительно хранить для каждого объекта простые пользовательские данные (типа строка, bool, int, double). Скоро еще появится возможность хранить для объекта сведения о его атрибутах.

Независимое хранение объектов геометрической модели обеспечивается следующим образом:

• внутри объекта записываются только те объекты, которые используются исключительно данным объектом;
• в случаях, когда геометрический объект ссылается на другой объект, в качестве ссылки на этот объект используется позиция его хранения в файле;
• объекты каждого уровня иерархии модели записываются в отдельное пространство, при необходимости в процессе записи файла можно переключаться между различными точками записи (рис. 5).

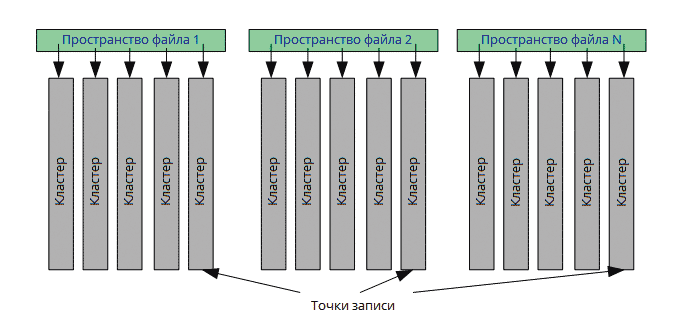
Рис. 5. Хранение объектов геометрической модели в расширенном формате C3D

Применение в области САПР

Разработанное API расширенного формата C3D предоставляет разработчикам приложений программные интерфейсы для загрузки оглавления модели из файла без чтения всей модели, выбора объектов по любым характеристикам, хранящимся для объектов в дереве модели, и чтения выбранных объектов. Поддерживается и обычное чтение модели целиком, причем возможна работа как с файлами C3D в расширенном формате, так и с файлами, записанными в стандартном формате C3D, за счет чего обеспечивается совместимость с более ранними версиями файлов.

На практике это означает, что при чтении файла в формате C3D можно загрузить и просмотреть дерево модели, затем выбрать, какие конкретно объекты (по наименованию, типу, размеру, атрибутам) необходимо прочитать и отобразить на экране, а уже потом прочитать выбранные объекты, используя информацию о позициях их хранения в файле (рис. 6).

Рис. 6. Загрузка геометрических объектов из файла C3D (по наименованию, типу или размеру)

Использование данного функционала позволит уменьшить время загрузки 3D­данных в САПР в тех случаях, когда пользователю необходимо частично прочитать информацию из файла, а не грузить всю модель целиком.

Обновленная структура расширенного формата C3D также позволит оптимизировать алгоритмы чтения и записи данных в формат C3D под многоядерную архитектуру. Функционал находится в стадии активного развития.

***

Следите за новостями C3D Labs на страницах журнала «САПР и графика» и на официальном сайте компании: http://c3dlabs.com/. На данном сайте вы можете БЕСПЛАТНО скачать приложение C3D Viewer для просмотра и конвертации 3D­моделей, а также взять на тестирование любой из лицензируемых компонентов C3D Toolkit для разработки инженерного программного обеспечения.