Моделирование процесса раскрытия подушек безопасности в SIMULIA Abaqus

Артем Кисловский, стажер, ООО «ТЕСИС»

Дмитрий Нуштаев, к.т.н, инженер, ООО «ТЕСИС»

Система пассивной безопасности защищает пассажиров транспортного средства от получения травм в результате аварии. Разработка новых поколений подушек безопасности неразрывно связана с проведением вычислительных экспериментов, которые используются для тестирования на всех этапах разработки изделия. Метод постоянного давления (UPM) и связный метод Эйлера — Лагранжа (CEL) применяются для двух основных типов анализа: In position (IP) и Out of Position (OoP). Первый тип анализа рассматривает ситуации, в которых пассажир взаимодействует с полностью раскрытой подушкой безопасности, а второй — с находящейся в стадии раскрытия. В отличие от UPM­метода, где значения термодинамических параметров приняты постоянными во всей области, CEL­метод использует традиционный эйлеров подход к описанию движения сплошной среды, в котором параметры вещества определяются для каждой ячейки расчетной сетки. Деформация лагранжевой оболочки зависит от приложенной к ней силы, которая вычисляется с использованием алгоритма общего контакта. Результаты CEL­подхода лучше согласуются с экспериментальными данными на всех стадиях раскрытия подушки безопасности, однако его применение для полностью раскрытой подушки безопасности (IP­анализ) нецелесообразно из­за высоких вычислительных требований алгоритма и незначительного влияния структуры внутреннего течения на результаты моделирования конечного этапа. На поздних стадиях раскрытия (IP­анализ) традиционно используется UPM­метод. Функционал программного комплекса SIMULIA Abaqus позволяет с высокой точностью моделировать задачи раскрытия сложных надувных конструкций с применением как CEL­ и UPM­подходов, так и их комбинации.

Введение

Стремительное развитие технологий приводит к улучшению комплексной безопасности автомобилей и пассажиров, которое достигается усовершенствованием как программных средств (например, использование искусственного интеллекта для предотвращения аварийных ситуаций), так и элементов конструкции автомобиля. Развитие беспилотных транспортных средств выдвигает особые требования к системе пассивной безопасности пассажира, основными элементами которой считаются ремни и подушки безопасности. В настоящее время безопасность является приоритетным направлением для автопроизводителей, выполняющих условия регулирующих норм и стандартов. Существующие требования технического регламента, действующего на территории Российской Федерации, согласуются с требованиями Правил Европейской экономической комиссии ООН. Одним из основных критериев оценки автомобиля, согласно принятой в ЕС программе (Euro NCAP), является обеспечение безопасности пассажиров. Впервые подушки безопасности были установлены в 1970­х годах на автомобилях компании Ford и в настоящее время относятся к обязательным элементам системы пассивной безопасности транспортных средств [1]. Современный автомобиль может быть укомплектован различными типами подушек безопасности (рис. 1), активация конкретного типа которых происходит в зависимости от положения области удара.

Рис. 1. Основные типы подушек безопасности легкового автомобиля и их устройство

Конструктивно подушка безопасности состоит из двух элементов: оболочки, обычно изготавливаемой из тонкой нейлоновой ткани, и пиропатрона (инфлятора), наполняющего ее газом. Идеальным считается сценарий, в котором взаимодействие пассажира происходит с полностью раскрытой оболочкой — in­position (IP) анализ. Потенциально опасная ситуация возникает, если пассажир находится слишком близко к подушке безопасности в момент ее раскрытия — out­of­position (OoP) анализ. В этом случае человек соприкасается с взрывообразно наполняющейся оболочкой. Срабатывание подушки безопасности происходит за относительно небольшой временной промежуток. В зависимости от начальных условий, время столкновения человека с поверхностью подушки происходит меньше чем за 30 миллисекунд. Столь короткий промежуток времени затрудняет сбор экспериментальных данных о процессах, происходящих на ранних стадиях раскрытия. Вычислительный эксперимент проводится с целью изучения физики внутреннего течения, его влияния на замкнутую сложенную оболочку и оценки степени ее воздействия на пассажира.

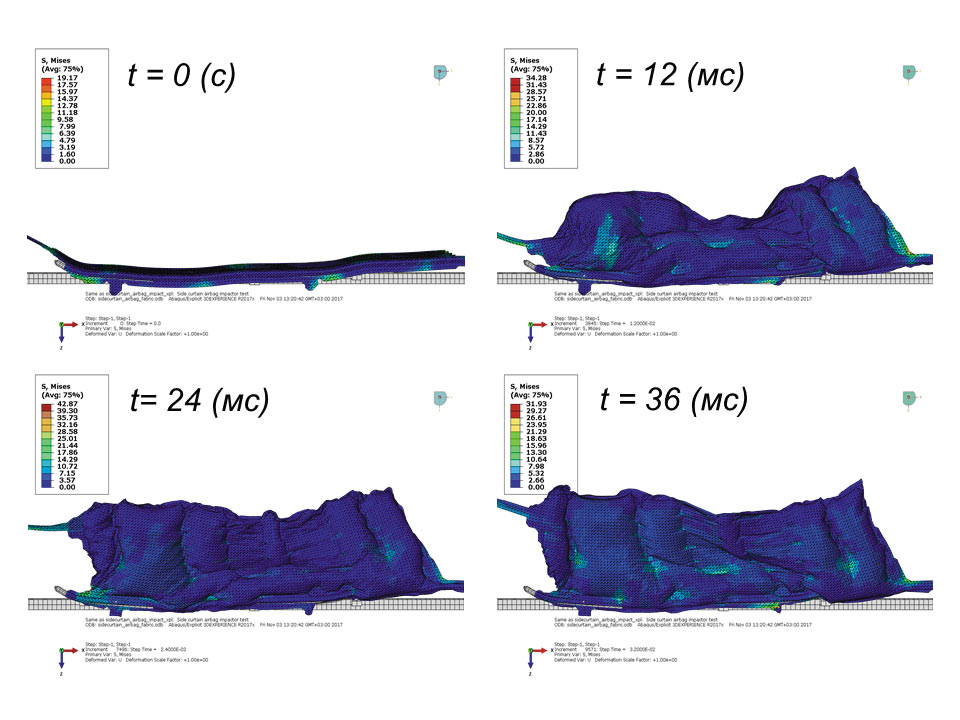
Рис. 2. Результат моделирования боковой подушки безопасности на разных стадиях раскрытия

В настоящее время существует несколько подходов к численному моделированию процессов раскрытия подушек безопасности. Первую группу составляют методы, аппроксимирующие внутреннее течение осредненными по пространству значениями термодинамических параметров, — метод постоянного давления UPM (англ. Uniform Pressure Method). Вторую группу образуют методы, моделирующие внутреннее течение вещества, — связный метод Эйлера — Лагранжа CEL (англ. Coupled Eulerian Lagrangian), гидродинамика сглаженных частиц SPH (англ. Smoothed Particle Hydrodynamics) [2].

Одним из лидеров решения задач моделирования надувных конструкций является программный комплекс SIMULIA Abaqus. Его инструментарий позволяет успешно моделировать сложные конструкции и сценарии: срабатывание боковой автомобильной подушки безопасности, состоящей из 18 отсеков (рис. 2), раскрытие многокамерной заглушки железнодорожного туннеля (рис. 3) [2]. В настоящей статье рассмотрены подходы к конечно­элементному моделированию процесса раскрытия подушек безопасности, приведено описание реализации UPM­ и CEL­методов в SIMULIA Abaqus, и выполнено сравнение результатов моделирования с экспериментальными данными для модели фронтальной однокамерной подушки безопасности.

Рис. 3. Полноразмерные модели заглушки железнодорожного туннеля: а — тестовые данные; б — результаты вычислительного эксперимента [2]

Метод постоянного давления (UPM)

Моделирование процесса раскрытия подушек безопасности осуществляется на базе конечно­элементных комплексов, использующих явную схему интегрирования уравнений движения по времени. Явные численные схемы хорошо подходят для решения высокоскоростных динамических задач с учетом множественных контактных взаимодействий и самоконтакта. В конце 1980­х годов была предложена математическая модель аппроксимации внутреннего давления на базе явной схемы — метод постоянного давления UPM, основанный на решении скалярных уравнений термодинамики [3]. UPM­метод имеет довольно простую численную реализацию и не требует больших вычислительных ресурсов, обладает достаточной точностью для задач, в которых эффектами, связанными с внутренним течением газа, можно пренебречь. Предположение о постоянстве давления и температуры во всей внутренней области ограничивает область применения UPM­метода. Несмотря на это, он нашел широкое применение при проведении IP­анализа вследствие относительно низких вычислительных затрат.

В программном комплексе SIMULIA Abaqus для использования UPM­метода необходимо определить полностью замкнутую область оболочки, аппроксимированную лагранжевыми элементами. Опорная точка, расположенная внутри области, используется для определения свойств наполняющего ее вещества (молярная масса, теплоемкость при постоянном давлении). Кроме того, в ней вычисляются термодинамические параметры газа, задаются характеристики инфлятора (устройства, наполняющего область газом), определяется утечка газа через материал. В задачах моделирования подушек безопасности газ считается идеальным, а процесс наполнения — адиабатическим, так как теплообмен отсутствует вследствие того, что расширение происходит за малый промежуток времени. На рис. 4 представлена схематичная модель замкнутой области, наполняемая через физический инфлятор. На каждом шаге по времени объем замкнутой области вычисляется методами прямого интегрирования, а масса газа определяется по закону сохранения массы: 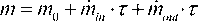, где 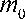 — масса газа, изначально находящегося в оболочке,  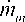и 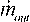 — массовый расход втекающего и вытекающего газа,  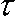— шаг интегрирования по времени. Уравнение состояния  совместно с уравнением адиабаты  образует замкнутую систему, позволяющую вычислить плотность, давление и температуру газа в замкнутой области на каждом временном шаге интегрирования [3]. В SIMULIA Abaqus существует четыре математические модели инфлятора, определяющие его массовый расход . В каждой модели задаются характеристики инфляционного газа, его состав и известные термодинамические параметры. Кроме того, в рамках UPM­метода возможно задать смесь газов, истекающую из инфлятора, отличную от начального состава замкнутой области.

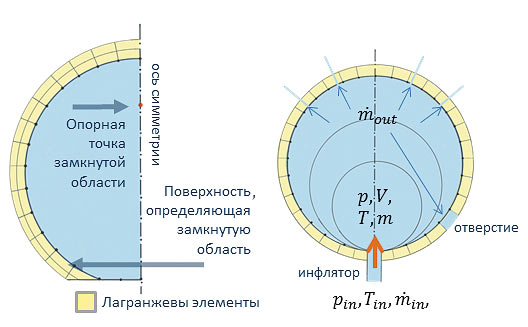
Рис. 4. Схематичное изображение UPM-метода

Метод UPM использовался для моделирования боковой подушки безопасности и заглушки железнодорожного туннеля (рис. 2 и 3). Его вычислительная эффективность позволяет рассматривать случаи с очень сложными внутренними структурами. Например, при моделировании боковой подушки безопасности (см. рис. 2) учитывались не только свойства инфлятора, утечка через материал и специальные отверстия между камерами и окружающей средой, но и возможность закупоривания оболочки. Данное явление происходит при самоконтакте ткани подушки безопасности, что препятствует течению инфляционного газа.

Связный метод Эйлера — Лагранжа (CEL)

В общем случае термодинамические параметры наполняющего подушку безопасности газа, влияющие на ее форму, являются функциями не только времени, но и координат, то есть 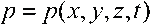, 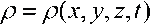. Для однозначного описания движения сплошной среды в программном комплексе SIMULIA Abaqus используется эйлеров подход, в котором скорость и термодинамические параметры свободно перемещающегося наполняющего вещества рассматриваются в фиксированных точках  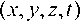 пространственно­временного объема — ортогональной эйлеровой сетки, охватывающей объект исследования. Материал подушки безопасности аппроксимируется лагранжевыми элементами, жестко связанными с ним.

В связном методе Эйлера — Лагранжа материал, определенный в ячейках эйлеровой области, взаимодействует с лагранжевыми элементами. Данный тип анализа можно разделить на три функциональных шага. Первый — Volume of fluid method (VOF) позволяет отслеживать форму и положение поверхности материала. Для этого вводится специальная дробная функция 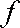, принимающая значения от 0 до 1 (рис. 5) в зависимости от состава эйлеровой ячейки: в ячейке, полностью заполненной веществом 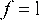, а в пустой 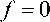. Лагранжевы элементы разбивают граничные эйлеровы ячейки на две области, граница между которыми определена однозначно. На втором шаге решаются уравнения движения жидкости и газа, определяются скорость и термодинамические параметры потока в ячейках, для которых 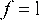, а значения на границе 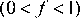, вычисляются в соответствии с выбранной математической моделью контакта. Сила, действующая на лагранжевы элементы, есть произведение давления на площадь границы раздела, вычисленной на первом шаге. Третий этап — определение деформаций и напряжений лагранжевого материала оболочки, вызванных внутренним состоянием вещества (давление в пределах одной ячейки считается постоянным). Лагранжева сетка деформируется, занимая новое положение в расчетной области на новом временном шаге. Далее процесс итеративно замыкается.

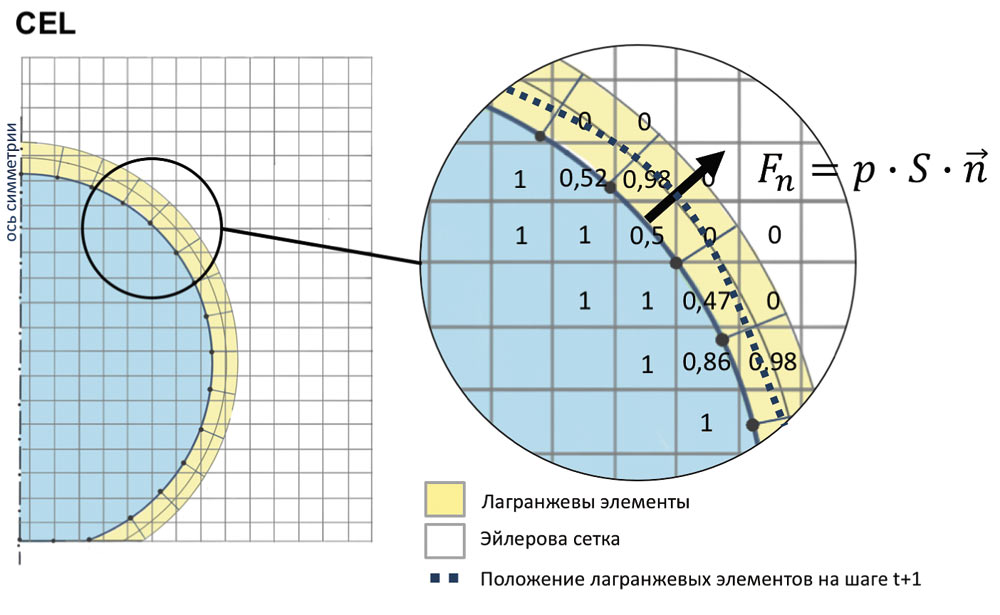
Рис. 5. Схематичное изображение CEL-метода

Функционал программного комплекса SIMULIA Abaqus позволяет проводить анализ для различных типов жидких и газообразных веществ. В зависимости от физико­математической формулировки задачи задаются свойства жидкости или газа (уравнение состояния, вязкость) и выбирается система уравнений, описывающая движение вещества (уравнения Навье — Стокса, Эйлера). Обычно при автомобильной аварии в инфляторе поджигается смесь азида натрия (NaN3), вследствие чего происходит химическая реакция с большим выделением газообразного горячего азота (N2), который наполняет подушку безопасности. С большой точностью азот можно считать идеальным двухатомным газом с известными свойствами. Его термодинамические параметры определяются путем решения уравнений Эйлера в узлах пространственной сетки.

Использование двух сеток и дополнительных систем уравнений в VOF, динамики движения среды и алгоритма контакта значительно увеличивает размерность CEL­задачи, по сравнению с UPM­методом. Проигрывая в вычислительной эффективности UPM­методу, CEL­метод достаточно точно разрешает задачу на ранних стадиях раскрытия подушек безопасности и используется в OoP­анализе.

На рис. 6 приведено сравнение расчетов, выполненных методами UPM и CEL, с экспериментальными данными [4]. В двух, вычислительных экспериментах использовалась идентичная конечно­элементная модель. Метод UPM определяет деформированную форму оболочки с относительно большой ошибкой на начальной фазе расширения, в то время как форма подушки безопасности, рассчитанная CEL­методом, соответствует экспериментальным данным. Однако конечная форма оболочки (рис. 6в), когда влияние структуры внутреннего течения несущественно (IP­анализ), в CEL­ и UPM­анализе идентична.

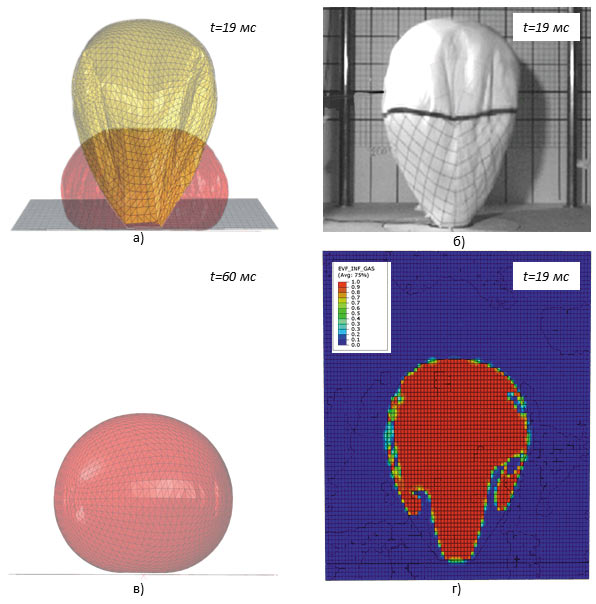
Рис. 6. Сравнение формы фронтальной подушки безопасности: а — CEL (желтый), UPM (красный); б — эксперимент; в — конечное состояние CEL (желтый), UPM (красный); г — состав эйлеровых ячеек

Верификация математической модели

В начале 1990­х немецкие автомобильные производители Volkswagen, DaimlerChrysler, Porsche, BMW и Audi создали рабочую группу для оценки и развития вычислительных методик OoP­экспериментов. Рабочая группа разрабатывала различные численные методы для моделирования эксперимента по раскрытию стандартной 60­литровой подушки безопасности. В работе [4] рассматривались две начальные конфигурации подушки безопасности: плоская и сложенная. Сверху помещался полусферический муляж, с которого проводилась запись экспериментальных данных — ускорений. Схема эксперимента приведена на рис. 7. Численное моделирование проводилось в программном комплексе SIMULIA Abaqus с использованием UPM­ и CEL­методов, а его результаты сравнивались с экспериментальными данными.

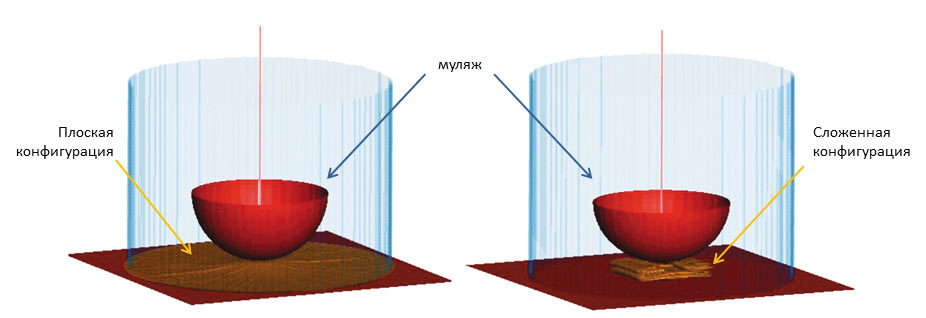
Рис. 7. Постановка физического эксперимента

Поверхность подушки безопасности была разбита на мембранные элементы. Использован нелинейный анизотропный материал оболочки *fabric. Данная модель является феноменологической моделью тканых ламинатов, которая учитывает влияние ориентации волокон на деформирование ткани. Функционал модели обеспечивает возможность моделирования линейно­упругого, нелинейно­упругого и упруго­«пластического» (с остаточной деформацией после разгрузки) поведения ткани. Согласно модели, локальные напряжения в ткани определяются как функция номинальных деформаций в направлении утка и основы, а также угла между волокнами (сдвиговой деформацией). Предполагается, что растяжение/сжатие вдоль основы/утка и работа материала на сдвиг независимы друг от друга, то есть поведение каждого компонента напряжений ткани зависит только от ее деформации в этом направлении. Эйлерова область представляет собой прямоугольную пространственную сетку, вытянутую на достаточно большое расстояние от границ объекта, давая ему возможность свободно перемещаться и деформироваться. Между наполняющим газом и поверхностью подушки безопасности определены контактные взаимодействия.

Рис. 8. Результаты физического эксперимента (черно-белое фото) с данными, полученными CEL-методом

Рис. 9. Зависимость ускорения модели от времени для плоского (а) и сложенного (б) начальных состояний подушек безопасности [4]

На рис. 8 приведены результаты физического эксперимента и численного моделирования методом CEL для двух начальных конфигураций. В эксперименте использовалась эйлерова сетка с размером ячейки 5 мм (диаметр модели подушки безопасности — 250 мм). На рис. 9 представлены зависимости ускорения муляжа от времени для двух начальных конфигураций подушки безопасности (плоская — слева, сложенная — справа). Для удобства ускорение выражено в единицах g (g = 9,81 м/с2). Согласно программе испытаний Euro NCAP [5], жестким ударом считается удар с величиной ускорения для головы, превышающей 80 g. Результаты, полученные UPM­методом, правильно отражают тенденцию изменения ускорений, однако имеют относительно высокую ошибку на ранних стадиях раскрытия, связанную с упрощениями, принятыми в математической модели. В то же время метод CEL верно определяет ускорения, оказываемые оболочкой подушки безопасности на муляж на всей стадии процесса. 

Литература:

1. Khan M.U., Moatamedi M. A review of airbag test and analysis //International journal of crashworthiness. 2008. Т. 13. №. 1. С. 67­76.
2. Sosa E.M., Wong C.S., Barbero E.J. Modeling of Confined Inflatable Structures. — SIMULIA Community Conference 2015.
3. Wang J.T., Nefske D.J. A new CAL3D airbag inflation model // SAE Technical Paper. 1988. № 880654.
4. Abaqus Technology Brief, TB­11­ABCEL­1, June 2011.
5. Euro NCAP Assessment Protocol — AOP, Version 8.0.2, November 2