Компьютерное моделирование тепловых и фазовых полей при непрерывном литье сляба

Алексей Монастырский
К.т.н., ведущий специалист, АО «СиСофт», г. Москва.

Представлена реализация математической модели процесса производства сляба шириной 2000 мм и толщиной 315 мм из стали марки 10Г2ФБЮ на установке непрерывного розлива стали (УНРС). В соответствии с документацией, заданы основные габариты установки, в том числе координаты осей нижнего ряда роликов, размеры кристаллизатора, протяженность зон вторичного охлаждения (ЗВО), расход воды в зонах ЗВО, тепловые и скоростные параметры техпроцесса, а именно:

• температура разливаемой стали — 1544­1538 °С;
• характерный химический состав стали: С­0,097%; Si­0,28;
  Mn­1,65; Cr­0,03; Ni­0,03; Cu­0,04; V­0,07; Ti­0,02; Nb­0,04; Al­0,04; N­0,005; P­0,012; S­0,002; As­0,002; Mo­0,003; Ca­0,0014;
• материал кристаллизатора — медь;
• материал приводных роликов — 40ХМФА, материал остальных роликов — 24ХМ1Ф;
• скорость розлива стали — 0,6 м/мин.

В рамках выполнения работы решено пренебречь трением сляба о стенки кристаллизатора, влиянием трения сляба о поверхности роликов, деформацией сляба в роликах (так называемое мягкое обжатие). Целью создания математической модели является получение инструмента, ориентированного на уровень технолога­литейщика, для изучения тепловых и фазовых процессов, связанных с передачей тепла от сляба к кристаллизатору и роликам с учетом их неидеального контакта и теплофизических свойств, отдачей тепла в окружающую среду (воздух и/или водо­воздушная смесь в зоне вторичного охлаждения). Рассматриваются процессы, связанные с затвердеванием сляба, включая выделение скрытой теплоты кристаллизации.

Математическая модель создана в рамках выполнения научно­исследовательской работы совместно с ПАО «Северсталь».

Построение 3D­модели УНРС

Для разработки математической модели, ее реализации в виде программного кода, а также для дальнейшей верификации на основе экспериментальных данных необходима трехмерная CAD­модель. Эта модель представляет собой геометрическую область, в которой планируется моделировать и изучать физические явления, связанные с протеканием технологического процесса. Построение эталонной CAD­модели выполнено в CAD­системе высокого уровня NX (версия 10.0, разработчик Siemens PLM Software).

Эскизы нижнего ряда роликов построены по данным таблицы координат их осей и значений диаметров, указанных на схеме УНРС. Огибающая линия роликов делится на пять участков: вертикальный участок (идет непосредственно после кристаллизатора), участок загиба сляба, радиальный участок, участок разгиба сляба и горизонтальный участок (зона мягкого обжатия) — рис. 1.

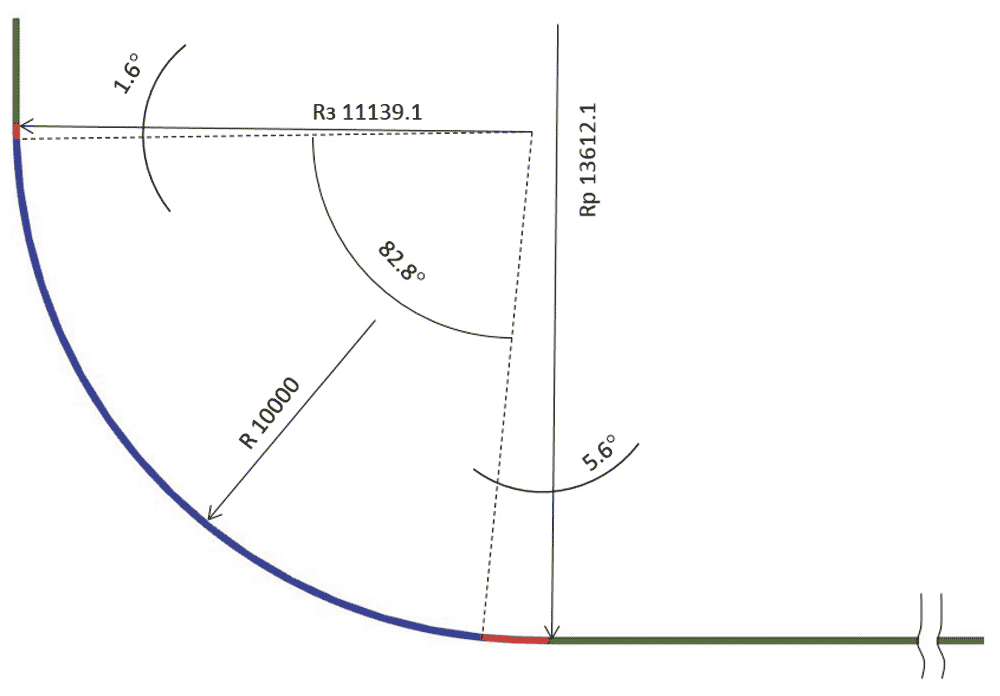
Рис. 1. Схема огибающей линии нижнего ряда роликов. Разными цветами показаны: линейные участки (вертикальный и горизонтальный) (зеленый); зона основного радиуса (синий); зоны загиба и разгиба сляба (красный)

Верхний ряд роликов может перемещаться, при этом настройка положения роликов зависит от размеров выпускаемого сляба. На схеме УНРС их положение никак не описано, поэтому при построении CAD­модели предполагается, что верхние ролики соосны с нижними роликами. При этом ось каждой пары роликов радиальных участков представляет собой радиус, проведенный из центра соответствующей окружности. На горизонтальном и вертикальном участке ось каждой пары сонаправлена вертикальной и горизонтальной оси соответственно.

Построение 3D­модели кристаллизатора не представляет трудностей. Принято решение не учитывать уклоны плит, поскольку уклон на сторону составляет от 1,2 мм (для широких плит) до 9,9 мм (для узких плит).

Построение объемной модели УНРС выполняется стандартными командами вытягивания элементов эскизов. На рис. 2 показана итоговая эталонная CAD­модель, на основе которой будет происходить построение конечно­элементной расчетной модели.

Рис. 2. Объемная CAD-модель УНРС

Разработка вычислительной технологии для моделирования тепловых процессов, протекающих в слябе, при движении его в УНРС

Одним из основных вопросов моделирования литейных процессов является решение задачи охлаждения и затвердевания отливки заданной конфигурации. Численные методы позволяют решить эту задачу на основе исходного уравнения нестационарной теплопроводности с соответствующими граничными условиями 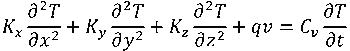[1]:

 ,                              (1)

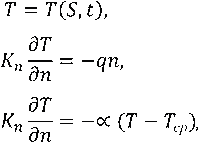
где x, y, z — координаты в области пространства, ограниченного поверхностью S;

n — нормаль к поверхности S;

t — время;

T — функция распределения температуры в пространстве координат x, y, z, t;

Kx, Ky, Kz, Kn — теплопроводность в направлении осей x, y, z и нормали n соответственно;

qv — объемная мощность внутренних источников теплоты;

Cv — объемная теплоемкость;

qn — граничный тепловой поток (по нормали к S);

α — коэффициент граничной конвективной теплопередачи в среду с температурой Tср.    

Кроме того, при решении задачи затвердевания наиболее важное значение имеет то, насколько адекватно учитывается выделение скрытой теплоты и теплопередача через границу сопряжения отливки и формы.

Одним из наиболее современных и часто применяемых численных методов для решения задач моделирования физических процессов является метод конечных элементов (МКЭ). Он используется в современных системах моделирования литейных процессов и хорошо подходит для задач, связанных с перемещением тел расчетной области относительно друг друга. Кроме того, метод конечных элементов является стандартом для создания моделей напряженно­деформированного состояния.

При создании математической модели процессов, протекающих в УНРС, за основу была взята математическая модель [1, 2] тепловых процессов, протекающих в отливке и форме и ее реализация для метода конечных элементов (КЭ). Эта модель была модернизирована для применения к условиям непрерывного литья.

При расчете температурных и фазовых полей (ТФП) в слябе, получаемом в УНРС, необходимо корректно учитывать движение металла внутри кристаллизатора, его выход в зону охлаждения и дальнейшее продвижение вдоль всей установки. Движение среды является главным отличием рассматриваемой задачи от задач моделирования литья фасонных отливок. В связи с этим требуется разработка новой вычислительной методики на базе МКЭ, которая позволит моделировать движение сляба в УНРС с учетом ее конструкции.

Для выбора оптимального варианта адаптации существующих вычислительных методик к условиям УНРС была разработана «транспортная» модель расчета тепловых полей, которая основана на использовании фиксированной КЭ­сетки, разбитой на слои (с одинаковым разбиением на КЭ внутри слоя) в продольном направлении сляба (рис. 3).

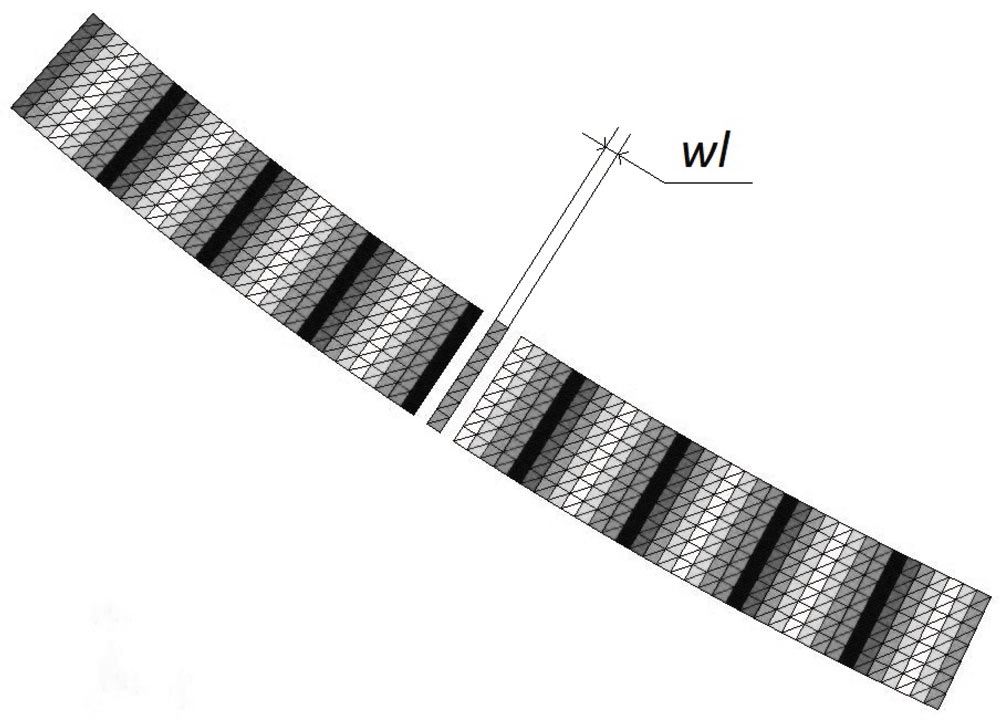
Рис. 3. Пример послойной структуры сетки сляба

При этом в расчете полей на каждом шаге моделирования участвуют только те слои, которые на текущий момент находятся в пространственной области, занятой слябом. Используемая структура сетки позволяет правильно описывать геометрию торца сляба и моделировать происходящие в нем тепловые процессы (в отличие от случая полностью неструктурированных сеток). Сдвиг ТФП вдоль траектории движения сляба реализуется наиболее просто в случае, когда шаг расчета по времени dt выбирается по формуле:

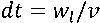,                               (2)

где wl  — толщина слоя;

v — скорость продвижения сляба.             

При таком выборе шага dt сдвиг расчетных полей осуществляется путем переноса узловых значений этих полей на следующий (по направлению движения) слой.

Основу для построения КЭ­сетки сляба, используемой в «транспортной» модели расчета ТФП в слябе, составляет огибающая линия нижнего ряда роликов, полученная на основе построенной CAD­модели УНРС (рис. 4).

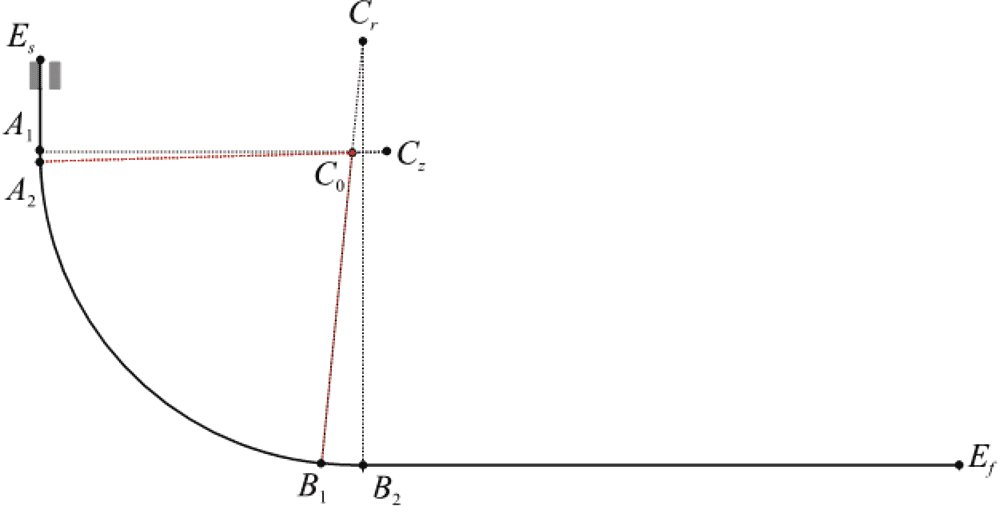
Рис. 4. Огибающая нижнего ряда роликов

Для построения в области сляба расчетной сетки, используемой в «транспортной» модели расчета ТФП, применяется параметрическое описание огибающей линии EsA1A2B1B2Ef. например, параметрическое описание дуг окружностей L1 = A1A2, L2 = A2B1, L3 = B1B2 имеет вид 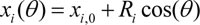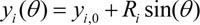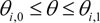(3):

, , ,           (3)

где значения параметров окружностей задаются пользователем.

Расчетная сетка в области сляба (см. рис. 4) получается в результате применения отображения к сетке, предварительно построенной в прямоугольном параллелепипеде (часть сляба), расположенном в кристаллизаторе. Пример КЭ­модели сляба представлен на рис. 5.

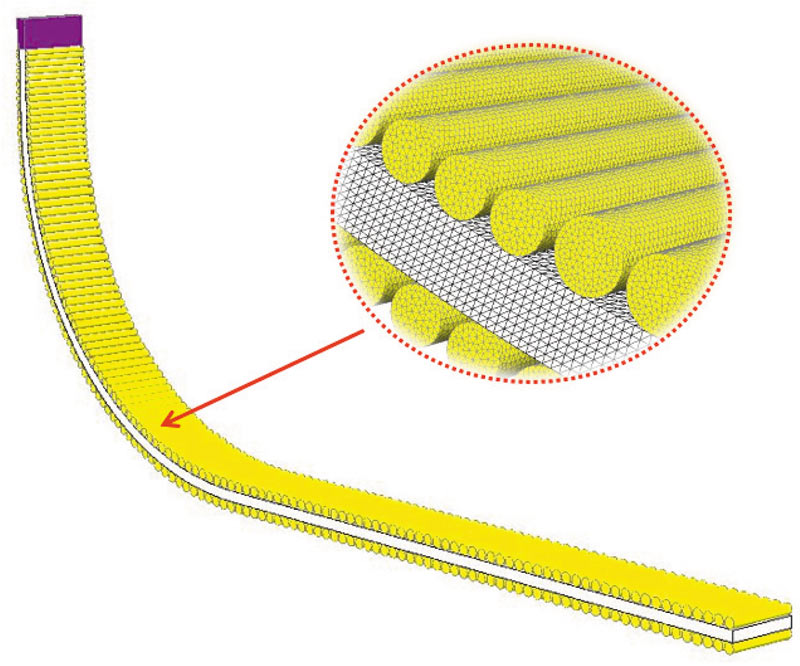
Рис. 5. Вариант сеточной модели расчетной области

Результаты расчетов и верификация модели

Условия расчетов, проведенных при тестировании разработанных алгоритмов и их верификации, задаются следующими параметрами:

• начальная температура расплава в кристаллизаторе;
• температура окружающей среды;
• скорость протяжки сляба;
• выдержка перед началом процесса (предстартовая выдержка);
• теплофизические свойства материалов (сляба, роликов, кристаллизатора);
• условия теплопередачи на поверхности «сляб — кристаллизатор»;
• условия теплопередачи на поверхности «сляб — ролики» в зоне ЗВО;
• условия теплопередачи на поверхности «сляб — ролики» вне зоны ЗВО;
• условия теплопередачи на поверхности «сляб — охлаждающая среда» в зоне ЗВО;
• условия теплопередачи на поверхности «сляб — среда» вне зоны ЗВО;
• условия теплопередачи на поверхности «боковая поверхность сляба — окружающая среда» в зоне ЗВО;
• условия теплопередачи на поверхности «боковая поверхность сляба — окружающая среда» вне зоны ЗВО;
• условия теплопередачи на поверхности «торец сляба — затравка».

На рис. 6 представлено ТФП расплава в кристаллизаторе перед началом движения затравки. Серым цветом показана твердая корка сляба.

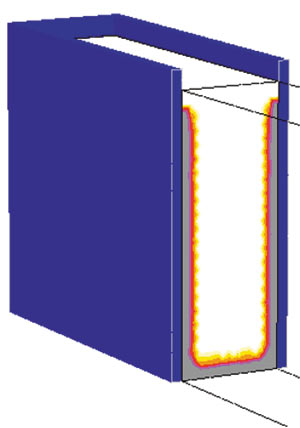
Рис. 6. Температурно-фазовое поле сляба перед началом движения (продольное сечение)

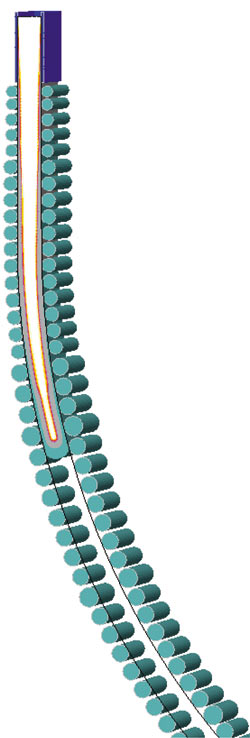
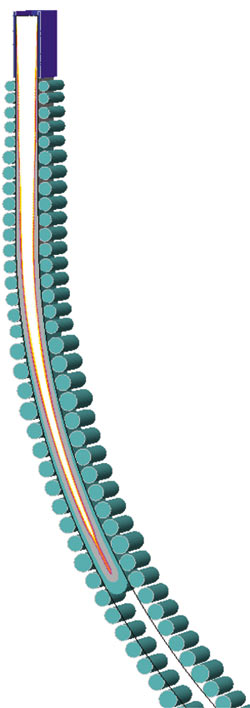
Результаты моделирования ТФП в движущемся слябе представлены на рис. 7. В соответствии с заданными условиями процесса стабилизация температурных полей в двухфазной зоне происходит задолго до того, как сляб достигнет последнего ролика. Это происходит на 1008­й секунде расчета. Язык жидкой фазы доходит до 37­го ролика, который, согласно документации, находится в зоне вторичного охлаждения.

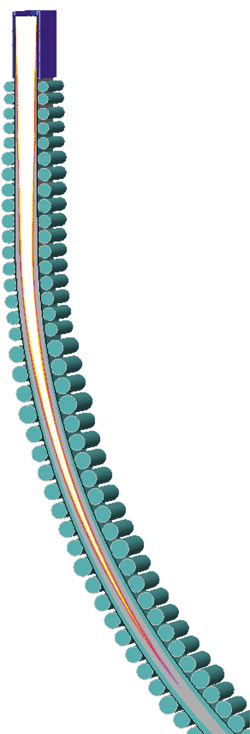t = 480 с	t = 720 с	t = 1008 с

Рис. 7. Температурно-фазовое поле сляба в процессе движения

На рис. 8 показаны температурные «пятна» в зонах контакта роликов со слябом в ЗВО. Как и предполагалось, ролики препятствуют охлаждению сляба, температура его поверхности локально повышается при контакте с роликами и затем вновь снижается под действием водовоздушной смеси. При удалении от ЗВО этот эффект смазывается.

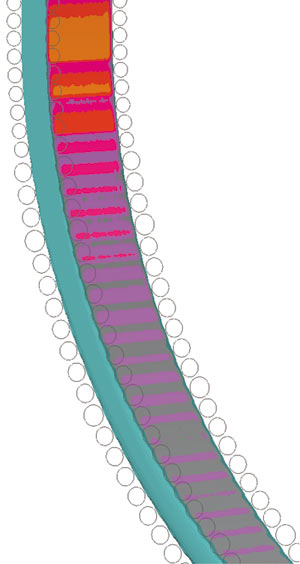
Рис. 8. Тепловые «пятна» в зонах контакта роликов со слябом

При моделировании тепловых процессов, происходящих в УНРС, важно использовать такие исходные параметры, которые соответствовали бы реальным технологическим условиям производства и, в частности, параметрам конкретного технологического процесса в конкретной установке. Часть таких исходных параметров регламентируется заранее известными параметрами технологии, например скорость протяжки, общая схема установки УНРС, геометрия сляба и элементов УНРС и т.п. Часть исходных параметров имеет достаточно универсальный физический смысл и не требует настройки под конкретный технологический процесс, например теплофизические свойства стали и др. Такие исходные данные являются так называемыми общими исходными данными и могут формироваться и использоваться пользователем без дополнительной коррекции под условия конкретного технологического процесса.

Однако при моделировании сложных физических процессов, протекающих в достаточно специализированных технологических условиях, которыми характеризуются УНРС, присутствуют исходные данные, требующие адаптации под конкретные производственные условия. При моделировании тепловых процессов в УНРС это относится к коэффициентам поверхностного теплообмена (коэффициенты теплопередачи) на различных участках сляба, а также между слябом и элементами УНРС. Хотя эти коэффициенты имеют четкий физический смысл, но применительно к УНРС носят суммарно­эффективный характер, так как включают возможные упрощения моделей (например, предположение о постоянстве температуры окружающей среды на некотором удалении) и не моделируемые в данной постановке процессы (например, течение и испарение воды на поверхности сляба). Определение коэффициентов теплопередачи на каких­либо простейших пробах для данного процесса малоэффективно, поскольку не отражает всей совокупности факторов, присутствующих при поверхностном теплообмене в УНРС в условиях принципиально разной и сложной системы охлаждения и теплообмена в различных зонах УНРС. Тем не менее в данных условиях (условиях УНРС) коэффициенты теплопередачи играют решающую роль при формировании тепловых полей сляба, которые собственно и являются главной целью моделирования тепловых процессов в УНРС.

В связи с этим совместно со специалистами ПАО «Северсталь» была принята следующая схема верификации модели, то есть подбора задаваемых коэффициентов теплопередачи. В заводских условиях специалисты ПАО «Северсталь» измерили температуры поверхности сляба в различных точках по его длине в так называемом установившемся (стационарном) режиме работы УНРС. Проведением необходимого числа расчетов коэффициенты теплопередачи, участвующие в модели, были подобраны так, чтобы результаты расчетов соответствовали измеренным температурам. Таким образом, обосновывается необходимая гибкость и адекватность алгоритмов модели.

Сложность проведения экспериментальных замеров температуры сляба не позволяет оценить их точность. Однако в данной ситуации любые полученные экспериментальные данные, даже вызывающие сомнение, должны показать общий характер процесса. А созданная модель должна воспроизводить этот процесс (пусть даже с погрешностью).

На рис. 9 представлены результаты замеров температуры по длине сляба.

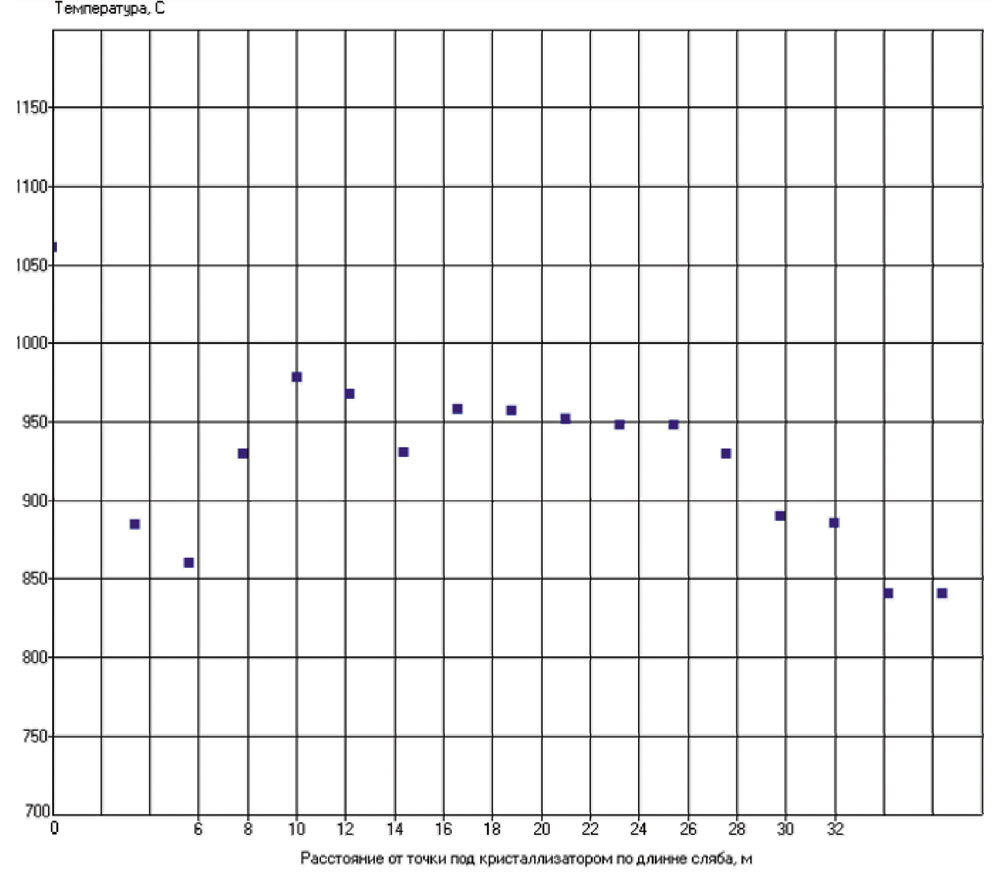
Рис. 9. Замеры температуры по длине сляба

Измерения проводились оптическим пирометром. В таких случаях достаточно трудно оценить их погрешность, так как она может зависеть от многих субъективных и объективных причин. Это и влияние дополнительных факторов (водяной пар, окалина и т.п.), и систематическая погрешность собственно прибора, которая для пирометров существенно зависит от эталонной шкалы. Считается, что самыми важными характеристиками пирометра, определяющими точность измерения температуры, являются оптическое разрешение и настройка степени черноты объекта. Коэффициент эмиссии ε (коэффициент излучения, степень черноты) — способность материала отражать падающее излучение. Он может принимать значения от 0 до 1. В литературе указывается, что применение неверного коэффициента эмиссии — один из основных источников возникновения погрешности измерений для всех пирометрических методов измерения температуры. На коэффициент излучения сильно влияет окисление поверхности металлов. Так, если для стали окисленной коэффициент составляет примерно 0,85, то для так называемой «блестящей» стальной поверхности он снижается до 0,075. Степень же черноты окалины в общем случае неизвестна, хотя обычно ее принимают как 0,8. Тем не менее будем считать, что общий характер распределения температур по длине сляба данные измерения отражают в основном правильно.

После проведения нескольких тестовых расчетов, в ходе которых менялись условия теплопередачи в разных зонах вторичного охлаждения и на границе «кристаллизатор — сляб», было достигнуто принципиальное соответствие расчетной температурной кривой экспериментальным точкам (рис. 10). 

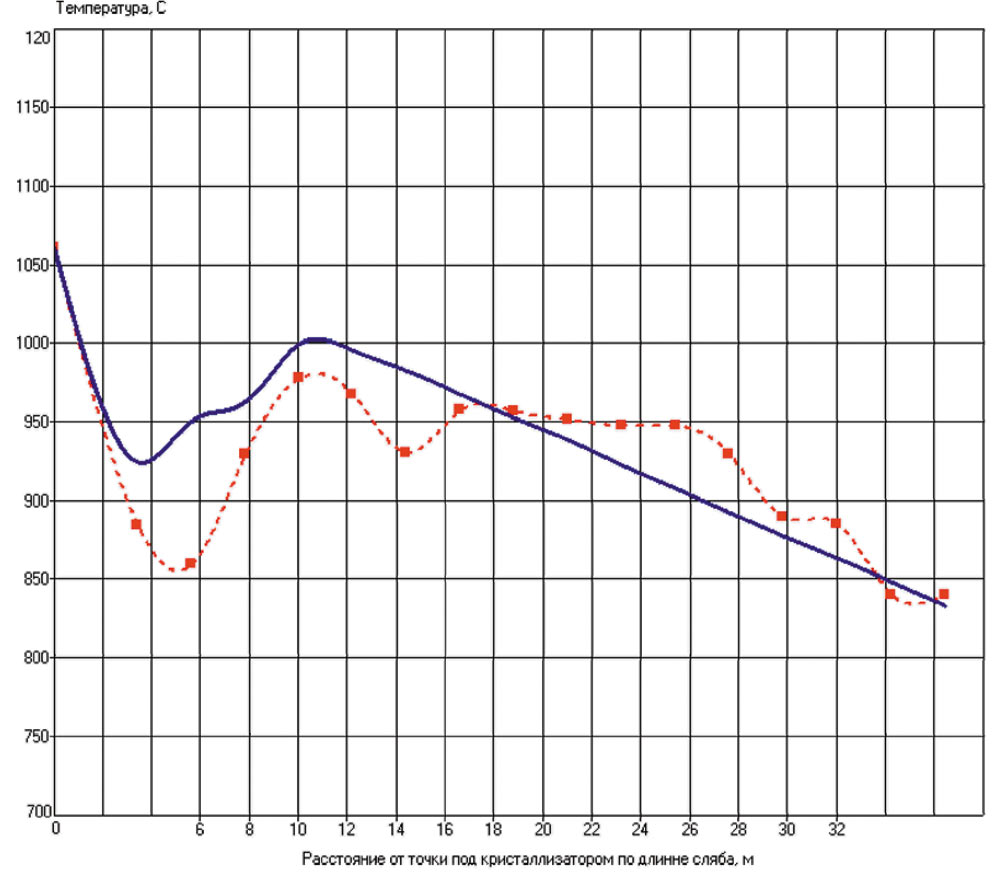
Рис. 10. Распределение температур по длине сляба по результатам расчета с верифицированными исходными данными (пунктиром показаны экспериментальные данные)

Список использованных источников

1. Тихомиров М.Д. Модели литейных процессов в САМ ЛП «Полигон». Труды ЦНИИМ, вып. 1. СПб: 1995. С. 21­26.
2. Тихомиров М.Д. Моделирование тепловых и усадочных процессов при затвердевании отливок из высокопрочных алюминиевых сплавов и разработка системы компьютерного анализа литейной технологии: Автореф. канд. дис. СПб: 2004. — 19