Влияние анизотропии свойств при совмещенном процессе обжима-раздачи

Валентин Маслов
К.т.н., доцент кафедры обработки металлов давлением, Самарский национальный исследовательский университет имени академика С.П. Королева.
Алексей Батурин
Студент, группа 1321, кафедра обработки металлов давлением, Самарский национальный исследовательский университет имени академика С.П. Королева.

В данной статье показаны результаты моделирования процесса изготовления концентрического трубного переходника методом обжима-раздачи, которое проводилось с помощью программы ANSYS-LS/DYNA. Выведена линейная зависимость величины деформации изменения толщины заготовки в нижней части (процесс раздачи) от коэффициента анизотропии свойств R.

Концентрические трубные переходники используют для расширения или сужения потока трубопровода в вертикальном положении. Они широко применяются при изготовлении трубопроводов. Одним из наиболее рациональных методов формообразования таких деталей является холодная штамповка из трубной заготовки. В процессе штамповки совмещают процедуру обжима и раздачи (рис. 1), что приводит к образованию разнотолщинности по краям детали. Непосредственное влияние на величину разнотолщинности имеет анизотропия свойств материала.

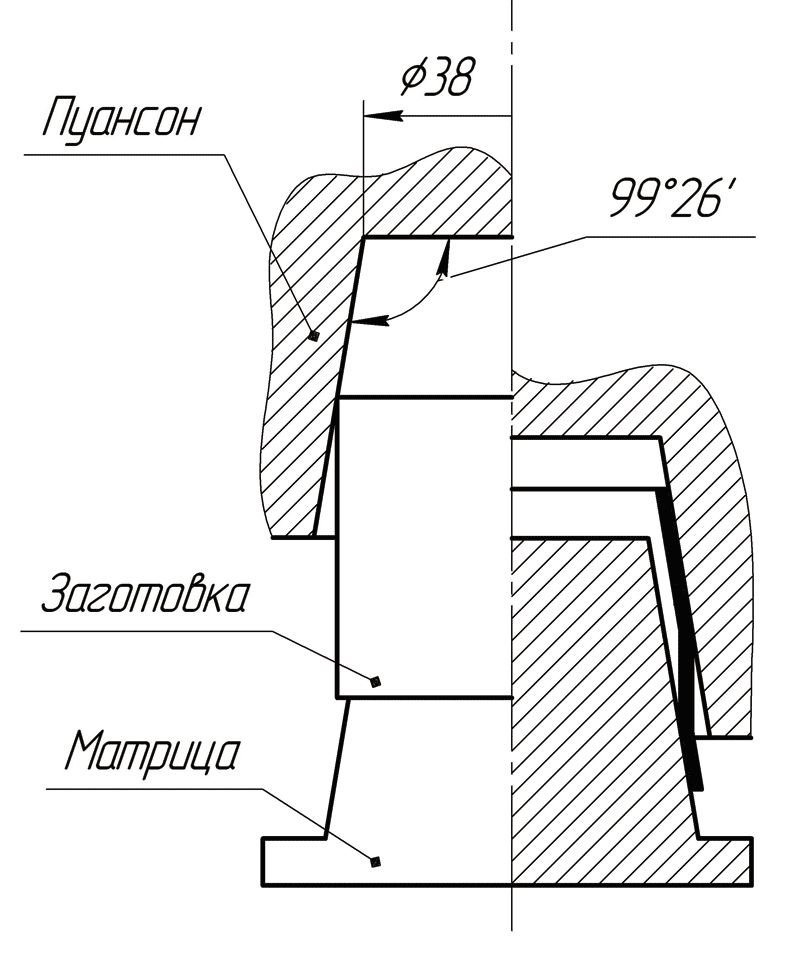
Рис. 1. Схема совмещенного процесса обжима-раздачи в исходном положении (слева); в процессе деформирования (справа)

В настоящей работе для определения напряженно­деформированного состояния заготовки использовано конечно­элементное моделирование процесса обжима­раздачи тонкостенного концентрического переходника с помощью программного продукта ANSYS­LS/DYNA.

Модель деформируемого металла при моделировании процесса — упрочняемый трансверсально­анизотропный материал (Transverse Anisotropic Material — материал с нормальной анизотропией свойств). Величина нормальной анизотропии исходной трубной заготовки задается коэффициентом Лэнкфорда [1]:

,

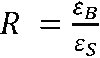где εB и εS — соответственно деформация сужения и деформация утонения образца при стандартном испытании на одноосное растяжение.

Деформационное упрочнение материала задается модулем упрочнения E’, который определяется по формуле [2]:

,

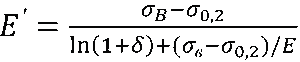где σB — предел прочности; σ0,2 — предел текучести; δ — относительное удлинение; E — модуль упругости.

В качестве примера для компьютерного моделирования была взята трубная заготовка диаметром 44,4 мм с толщиной стенки 1,5 мм и высотой 38,5 мм из нержавеющей стали Х18Н10Т. Конечные размеры детали: диаметр узкой части 38 мм, широкой части 50,8 мм, угол конусности α = 18°53’. Данная сталь имеет следующие механические свойства: σ0,2 = 195 МПа; σB = 549 МПа; E = 198 ГПа; δ = 35%; E’ = 1172,6 МПа; μ = 0,29. За материал рабочих частей штампа принимали инструментальную сталь У8А со следующими характеристиками: E = 206 ГПа; μ = 0,28. Его считали жестким.

Для моделирования деформируемой заготовки выбран элемент SHELL 163 — оболочечный элемент с четырьмя узлами, возможностью изгиба и пружинения. Геометрия оснастки и заготовки построена в LS­PrePost V4.2. Общее количество элементов — 954.

Воспроизведены три варианта процесса изготовления концентрических трубных переходников из нержавеющей стали Х18Н10Т с различными значениями коэффициента анизотропии свойств R: R1 = 0,5; R2  = 1; R3  = 3. При прочих равных условиях процесса формообразования изменялась только величина коэффициента нормальной анизотропии свойств R.

Моделирование данного процесса дает возможность определить величины деформаций и напряжений в любой точке деформируемой заготовки в любой момент времени процесса. Для сокращения времени анализа напряженно­деформированного состояния моделирование выполнялось на ¼ части заготовки (рис. 2).

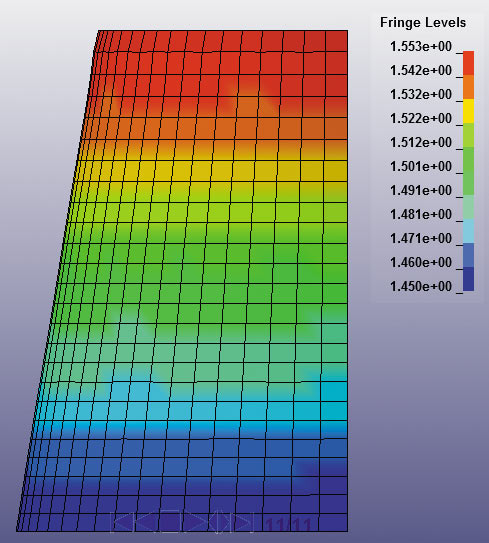
Рис. 2. Модель четверти деформируемой заготовки

Толщины изменились по всей длине заготовки, в наибольшей степени — по краям. В верхней части детали утолщение, а в нижней — утонение. Именно по изменению толщины и анализируется влияние анизотропии на деформированное состояние заготовки.

Графические зависимости изменения толщины по всему сечению при формообразовании концентрического трубного переходника из заготовки, имеющей различные значения величины анизотропии свойств R, приведены на рис. 3.

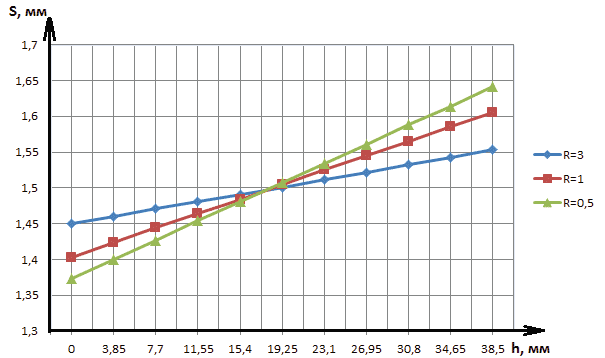
Рис. 3. Изменение толщины на различных участках заготовки в зависимости от коэффициента анизотропии свойств

Анализ графических зависимостей, приведенных на рис. 2, показывает, что минимальное изменение толщины имеет материал с коэффициентом анизотропии свойств R = 3. Максимальное изменение толщины у стали с коэффициентом анизотропии свойств R = 0,5.

В анализе используются логарифмические деформации изменения толщины:

 ,

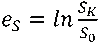где S0 — начальная толщина; SK — конечная толщина.

Результаты анализа толщины, а также деформаций изменения толщины деформируемых заготовок, полученные в результате моделирования процесса формообразования, приведены в табл. 1.

Таблица 1. Значения толщины и деформаций изменения толщины в центре, верхнем и нижнем краях

Таблица 2. Расчетный бланк для определения коэффициентов уравнения методом наименьших квадратов для нижнего края

Построим аналитическую зависимость изменения деформации по толщине на торце заготовки. Примем допущение, что эта зависимость деформации изменения толщины от показателя анизотропии R на торце заготовки имеет линейный закон, то есть ее можно описать уравнением:

y=ax+b,

где y —деформация изменения толщины eS; x — показатель анизотропии R; a, b — коэффициенты уравнения.

Для определения коэффициентов уравнения результаты моделирования обработаны методом наименьших квадратов.

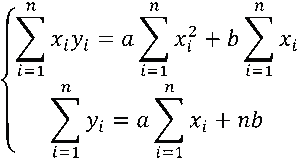(1)

Расчетный бланк для решения нормальных уравнений приведен в табл. 2.

Подставив значения деформаций из табл. 2 в систему нормальных уравнений (1), найдем значения коэффициентов a и b:

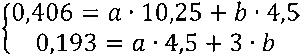 (2)

Отсюда получим:

a=0,0337

b=0,0138

Таким образом, линейная зависимость величины деформации изменения толщины заготовки в нижней части (процесс раздачи) в зависимости от анизотропии свойств R будет иметь следующий вид:

eS (раздаваемая сторона) = 0,0337 Ѕ R + 0,0138

Разработанная аналитическая зависимость позволяет определить деформацию изменения толщины анизотропной трубной заготовки при формообразовании концентрического трубного переходника.

Литература:

1. Гречников Ф.В. Деформирование анизотропных материалов. М.: Машиностроение, 1998. 448 с.: ил.
2. Формообразование нормализованных элементов трубопроводных систем на универсальных гидропрессах. Технологические рекомендации. Харьковский филиал НИАТ. Харьков, 1985. 83 с.
3. Попов И.П., Маслов В.Д., Севериненко А.Ю. Применение CAD/CAE­систем в исследовании процессов формообразования тонкостенных тройников // САПР и графика. 2012. № 1. С. 86­88.