Математический этюд. Экстравагантная константа ожерелья окружности

Виктор Чебыкин,
инженер, Новосибирск

Чем я занимался эти три года

Последние мои статьи, которые были опубликованы в журнале «САПР и графика», были посвящены теме овальных кривых. Напомню две из них: «А не замахнуться ли нам на Габриеля нашего Ламе?» (САПР и графика» № 8’2013), «Классификация и идентификация эллипсовидных овальных кривых» (САПР и графика), № 3’2014.

Эту тему я продолжил в статьях на сайте isicad.ru, причем планировал опубликовать одну­две, а получилось… 30, что называется — затянуло. Была мысль посылать статьи одновременно на isicad и в «САПР и графика», но посчитал это некорректным, может быть и зря. А чередовать, публиковать статьи, в которых продолжается одна тема, в разных изданиях — это всё равно, что публиковать главы романа поочередно в двух журналах.

Тем, кто помнит те статьи и интересна затронутая в них тема, вкратце расскажу, как я развивал эту тему, и что удалось сделать.

В этих статьях предложен ряд новых геометрических фигур, в том числе: несколько овалов, объединенных в группу овалов стабильной формы; антиэллипс; две секансоподобные кривые и др. Я описал их свойства, определил константы и координаты фокусов.

Кроме того, провел исследования нескольких известных кривых (кривые Ламе, овалы Максвелла, овал Кассини, цепная линия), выявил некоторые новые их свойства.

Предложил также новый метод определения наличия и местоположения фокусов овальных кривых — метод акульих зубов [1]. Этот метод позволил также получить новые геометрические фигуры: линии — определители фокусов. Последние, к тому же, являются хорошим подспорьем (инструментом) в вопросе идентификации овальных кривых. Метод нашел у всех симметричных (хотя бы относительно одной оси) овалов фокусы 3­й категории — фокусы ортогональных лучей. У гиперовалов найдены фокусы 2­й категории — фокусы двойного отражения лучей. Считавшийся долгое время бесфокусным, овал R­0 приобрел свои заслуженные два фокуса. Эллипсы, всегда считавшиеся двухфокусными, благодаря методу, стали шести­ (или четырех­) фокусными. Количество фокусов определяется как удвоенное число пересечений одной ветви линии­определителя с контуром овала и большой осью. Исключением является окружность: у нее, при одном имеющемся пересечении контура, определяется окружность расположения бесчисленного множества фокусов 3­й категории (своеобразный «пояс астероидов»).

Предложил классификацию фокусов овальных кривых, разбив их на четыре категории: высшая, первая, вторая и третья.

В одной из статей я предложил читателям «геометрический диктант» [2]. Поскольку вопросы диктанта были специфическими (по правильным многогранникам и овалам), он, по моим сведениям, не особо заинтересовал читателей. Это была проба, пусть и не совсем удачная.

Желающие получить более подробную информацию по упомянутым выше вопросам, могут открыть сайт isicad.ru, зайти в раздел «Авторы», нажать мою фамилию, и любая из 30 статей будет доступна для чтения.

Кривая «ожерелье окружности», ее константы и способ идентификации

Кривая «ожерелье окружности» была впервые предложена автором в статье «Математический этюд: Аксельбант фокинона и ожерелье окружности» [3]. Такие названия получили линии — определители фокусов овала фокинон и окружности.

Первое «ожерелье окружности» было построено по 95 точкам (рис. 1).

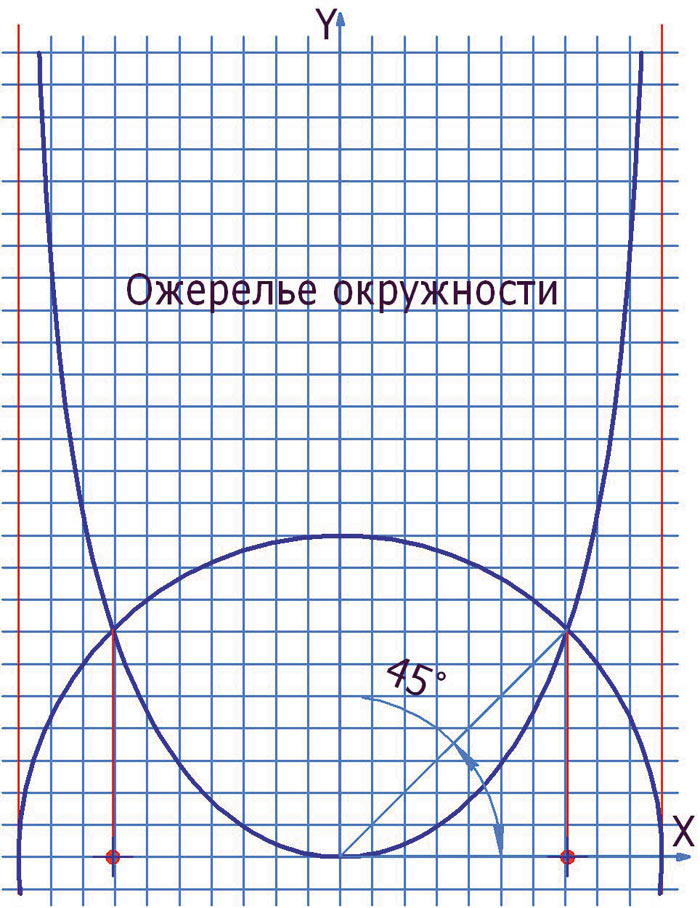
Рис. 1

Выяснилось, что по форме кривая близка графику одной из тригонометрических функций — секанса. Позднее появилась еще одна кривая подобной формы — «портупея циклопа». Эти три внешне похожие кривые имеют разную геометрию.

Константы кривой «ожерелье окружности»:

• отношение площади, отсекаемой производящей окружностью от «ожерелья окружности», к площади, производящей окружности Sоо/Sо = 1/π;
• отношение площади, отсекаемой производящей окружностью от «ожерелья окружности», к площади квадрата, вписанного в производящую окружность Sоо/S□ = 1/2;
• отношение дуги, отсекаемой производящей окружностью от «ожерелья окружности», к длине окружности Lоо/Lо = 0,34000329…

Если первые две константы были определены ранее, то третья приводится впервые в этой статье. При определении значения константы сразу бросились в глаза три ноля. Первое предположение было таким: из­за малого количества точек построения кривой за нолями появились цифры, отличные от 0, и при увеличении их (точек) числа константа придет к значению 0,34. Но эта версия оказалась ошибочной: увеличение числа точек до 201 дало только смену девятого знака с 8 на 9.

Вот так константа! Даже знаменитое Архимедово число π не позволило себе такого — иметь три ноля подряд в самом начале; у него они встречаются впервые в районе шестисотого знака, а тут — 4, 5, 6!

Поудивлялись… теперь перейдем к идентификации секансоподобных овальных кривых. На рис. 2 изображены «ожерелье окружности», «портупея циклопа» и секансоида.

Рис. 2

Масштабы их отображения разные, асимптоты где­то затерялись, производящие «овалы ожерелья» и «портупеи» тоже исчезли. Можно ли распознать эти кривые?

Можно. Начнем с «ожерелья». Обратите внимание на угол между прямой, соединяющей вершину «ожерелья» с точкой пересечения его с производящей окружностью и горизонталью (см. рис. 1). Угол равен 45°. Вот под таким углом из вершин всех кривых проведем отрезки до пересечения с контурами кривых. Далее построим окружности с центрами в вершинах с радиусами, равными этим отрезкам. Измерим площади, отсекаемые окружностями от кривых, и площади окружностей. Вычислим соотношения. Та из кривых, указанное соотношение которой будет равно 1/π, и будет являться «ожерельем окружности». Можно использовать и соотношения дуг, и третью константу «ожерелья».

Из двух оставшихся кривых выявим «портупею» похожим способом. Угол берем с рис. 3.

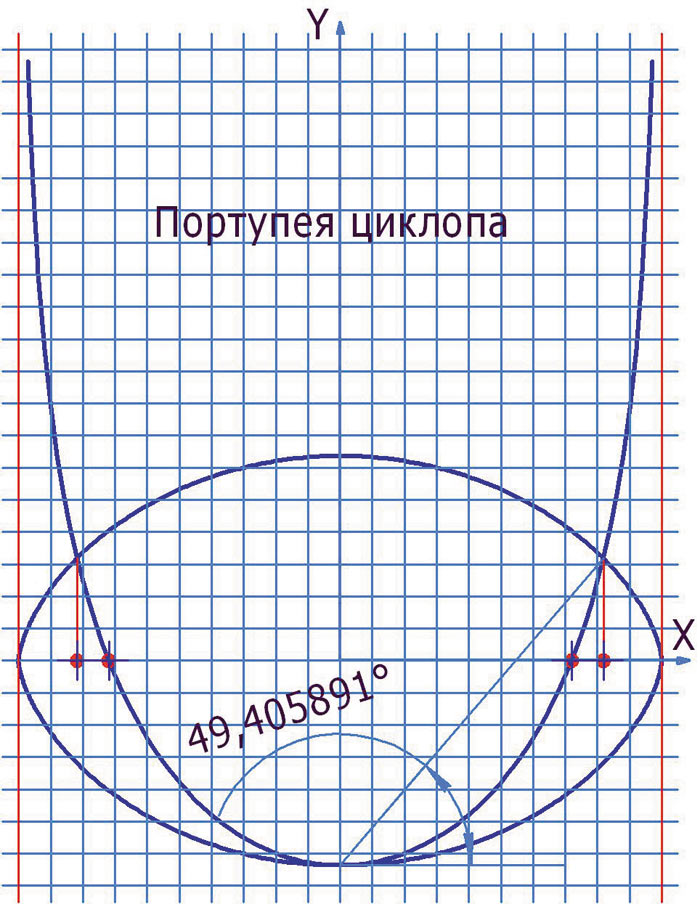
Рис. 3

Проводим под этими углами отрезки из вершин кривых до пересечения с контурами, измеряем эти отрезки и аналогичный отрезок на эталонном циклопе, находим соотношения, вставляем эталонный циклоп (масштабируя по соотношениям), совмещая полюс малой оси циклопа с вершинами кривых. Измеряем площади, отсекаемые циклопами от кривых, и площади циклопов, находим соотношения. Та кривая, у которой указанное соотношение будет равно π/4 (константа «портупеи циклопа»), и будет «портупеей циклопа».

Идентификация завершена. На рис. 4 исследуемые кривые изображены в одном масштабе. 

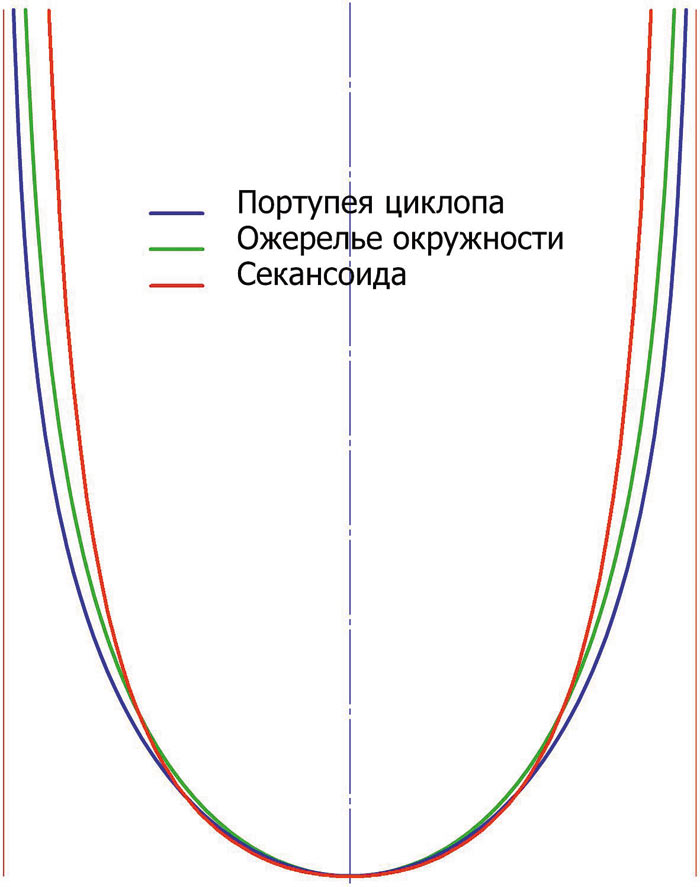
Рис. 4

Библиографический список:

1. Чебыкин В. Метод акульих зубов. isicad.ru, июнь, 2017.
2. Чебыкин В. Новогодний геометрический диктант. Овалы и многогранники. isicad.ru, декабрь, 2016.
3. Чебыкин В. Математический этюд: Аксельбант фокинона и ожерелье окружности. isicad.ru, октябрь, 2017