Евгений Якуничев, инженер-конструктор, Кузнечевский комбинат строительных конструкций и материалов, г.Архангельск

Программа AutoCAD широко известна во всем мире. Это одна из самых первых САПР, предназначенных для персональных компьютеров. Достаточно сказать, что первоначальная версия была выпущена еще для операционной системы MS DOS. С тех пор, постоянно совершенствуясь, программа обрела огромную популярность среди миллионов пользователей: конструкторов, проектировщиков, дизайнеров, землеустроителей, преподавателей, студентов и школьников. Наиболее ценные ее особенности: универсальность, надежность, нетребовательность к ресурсам компьютера, удобный интерфейс, не слишком высокая стоимость. Автор данной статьи также входит в число благодарных пользователей AutoCAD (с 2004 года), не переставая открывать для себя какие­то новые особенности и возможности, отмечая, насколько умно и толково действовали разработчики.  Являясь инженером­конструктором на предприятии, выпускающем железобетонные строительные конструкции, автору иногда приходится сталкиваться с необходимостью рассчитать тот или иной элемент на прочность и жесткость. Каждый, кто когда­либо выполнял расчеты в «Сопротивлении материалов», согласится, что это трудоемкий процесс, связанный со значительным количеством вычислений. Для определения деформаций конструкций под действием нагрузки часто используется графоаналитический метод Верещагина. Суть его на самом простом примере такова. Пусть некоторая балка находится под действием нагрузки, равномерно распределенной по ее длине (рис. 1). Требуется найти прогиб в точке С балки.

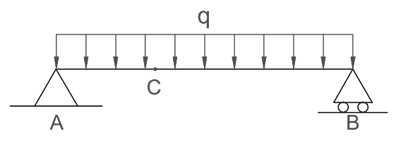
Рис. 1. Двухопорная балка под действием распределенной нагрузки

Вначале в нескольких точках балки определяются изгибающие моменты и строится эпюра этих моментов (грузовая эпюра). Затем строится еще одна эпюра изгибающих моментов, но уже от действия силы, модуль которой равен 1 (единичной силы), приложенной в точке, перемещение которой нужно определить (рис. 2).

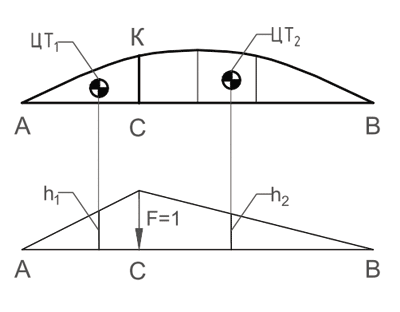
Рис. 2. Грузовая эпюра и эпюра от действия единичной силы

В соответствии с методом, предложенным в 1924 году талантливым ученым и изобретателем Андреем Константиновичем Верещагиным (в то время еще студентом Московского института инженеров транспорта), перемещение любой точки балки постоянного сечения равно:

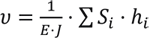 , (1)

где: E — модуль упругости материала; J — момент инерции сечения балки; Si — площадь грузовой эпюры на участке балки; hi — ордината эпюры единичной силы, находящаяся под центром тяжести эпюры Si .

Для нашего примера следует:

1) площадь фигуры АСК умножить на ординату h1;

2) площадь фигуры СКВ умножить на ординату h2;

3) результаты сложить и затем разделить на произведение E*J.

Аналогично можно определить угол поворота поперечного сечения балки в точке С. Для этого следует вместо единичной силы приложить в точке С единичный вращающий момент и построить соответствующую эпюру.

Однако в том случае, когда балка испытывает сложную нагрузку (различные сосредоточенные силы; распределенные на разных участках нагрузки; пары сил в каких­либо точках балки), определить площади и положение центров тяжести суммарных эпюр довольно трудоемко. Например, рассмотрим балку (точнее, расчетную схему), изображенную на рис. 3. Требуется определить прогиб балки в точках С и D, а также угол поворота сечения в точке В [1].

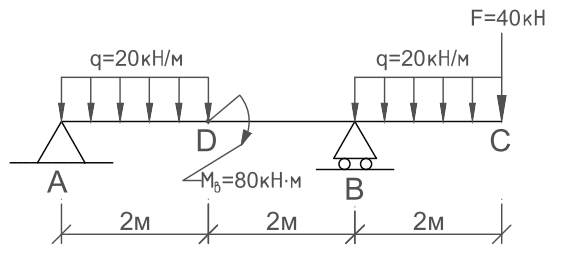
Рис. 3. Балка под действием сложной нагрузки

После определения опорных реакций построим суммарную эпюру изгибающих моментов, эпюры единичных сил, приложенных в точках С и D, а также эпюру единичного момента в точке В — это не составляет никакого труда (рис. 4).

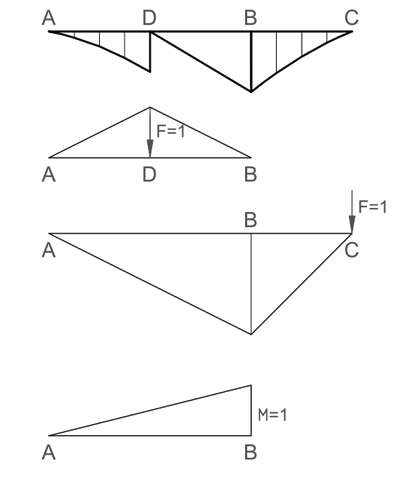
Рис. 4. Грузовая эпюра и эпюры от действия единичных сил и единичного момента

А вот далее, при традиционном способе решения, следует «расслоить» сложные эпюры на простые, затем каждую «перемножить» по специальным формулам на соответствующую единичную эпюру, затем результаты сложить, и так для каждого участка. Очевидно, при этом легко как запутаться, так и совершить ошибку. Но тут на помощь приходит AutoCAD. Ведь в нем имеются средства, позволяющие вычислить и площадь фигуры, и положение ее центра тяжести.

Для начала начертим в программе последовательно отрезки AD, DB и ВС, соответствующие участкам балки, длиной 2 единицы каждый. Построим на каждом участке по нескольким точкам контуры эпюры изгибающих моментов (на участках АD и ВС по пяти точкам; на участке DВ достаточно двух точек, так как эпюра здесь прямолинейна). Ординаты точек можно масштабировать, то есть уменьшить в 10 или 100 раз по сравнению со значениями соответствующих изгибающих моментов, чтобы эпюры не были слишком «вытянуты» по вертикали. С помощью команды Область (одноименная кнопка  на панели инструментов Черчение) из линий контура эпюры для каждого участка создаем замкнутые объекты; далее, применяя команду Геометрия и масса (кнопка  на панели инструментов Сведения), определяем площадь и положение центра тяжести каждого объекта (рис. 5). Для удобства перед каждым определением следует начало координат поместить в начальную точку соответствующего участка.

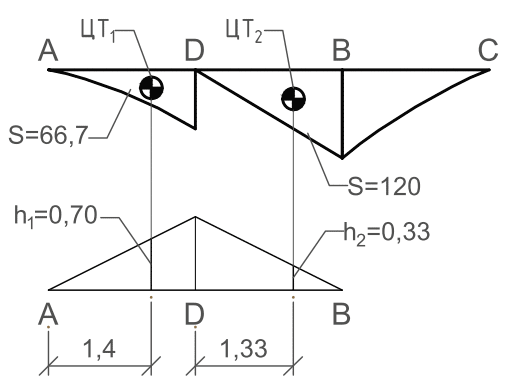
Рис. 5. Определение с помощью AutoCAD прогиба в точке D

Особенно преимущество данного метода проявляется при расчете прогиба балки в точке С и угла поворота сечения В. В самом деле, вместо того, чтобы производить вычисления по каждому из участков АD и DВ раздельно, определяем инструментом Геометрия и масса суммарную площадь эпюры на этих участках и положение центра тяжести этой сложной фигуры (рис. 6). При определении ранее прогиба в точке D так сделать было нельзя, поскольку эпюра единичной силы имеет в этой точке «перелом», в отличие от эпюры единичной силы, приложенной в точке С, и эпюры единичного момента, приложенного в точке В.

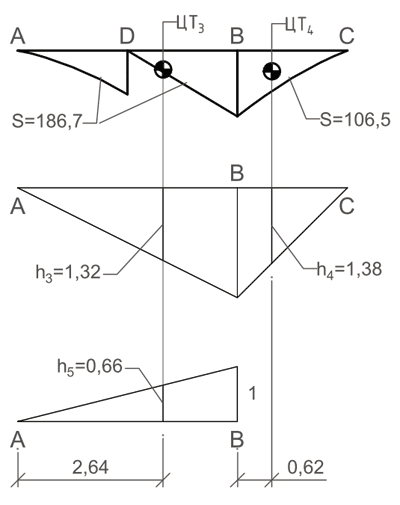
Рис. 6. Определение с помощью AutoCAD прогиба в точке С и угла поворота сечения в точке В

Осталось по формуле (1) вычислить искомые прогибы (не забывая увеличить площади в 10 или 100 раз, ведь мы масштабировали ординаты):

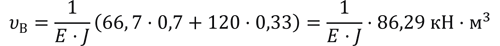
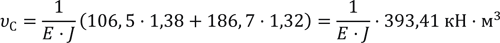
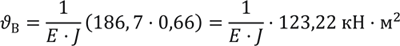
Учитывая, что модуль упругости стали Е = 2·105 МПа = 2·1011 Н/м2,
а момент инерции поперечного сечения балки J = 13380 см4 = 13,38·10­5м4 (принят двутавр № 36), окончательно получим:

υВ = 3,22·10­3 м (перемещение — «вверх»);

υС = 14,70·10­3 м (перемещение — «вниз»);

θВ = 4,60·10­3 рад (по часовой стрелке).

Результаты практически совпадают с вычисленными по специальным формулам [1].

Метод также прошел проверку на более сложном примере, показанном на рис. 7 [2]. Максимальная разница с ответами, полученными традиционным способом решения, составила менее 1% при существенно меньших затратах труда.

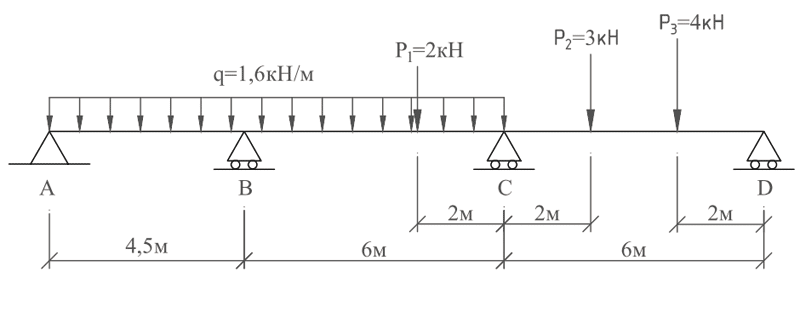
Рис. 7. Статически неопределимая балка со сложной нагрузкой

Вывод

Как оказалось, AutoCAD не только позволяет создавать качественные чертежи и 3D­модели, но и может оказать серьезную помощь в выполнении расчетов, в частности при решении задач «Сопротивления материалов». 

Литература:

1. Степин П.А. Сопротивление материалов / Учебник для немашиностроит. спец. вузов. 8­е изд. М.: Высшая школа, 1988.
2. Мухин Н.В. Статика сооружений в примерах / Учебное пособие для техникумов. М.: Высшая школа, 1972.