Создана ЗDмодель нового (предположительно) геометрического тела, получившего название «параболический тетраэдр» (рис. 1).
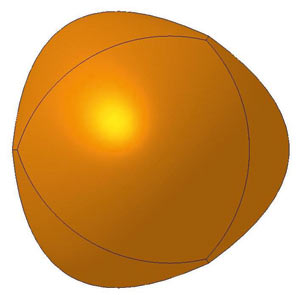
Рис. 1. Параболический тетраэдр
Основаниями тела служат не плоские треугольники, как у обыкновенного тетраэдра, а поверхности параболоидов. Параболический тетраэдр имеет четыре поверхности параболоида, шесть ребер, четыре стыковые вершины, в которых сходятся ребра. Кроме этих вершин, благодаря форме параболоида, он располагает четырьмя дополнительными вершинами, являющимися доминантными. Стыковые же вершины незначительно выделяются на поверхности тела, в отличие от вершин обыкновенного тетраэдра.
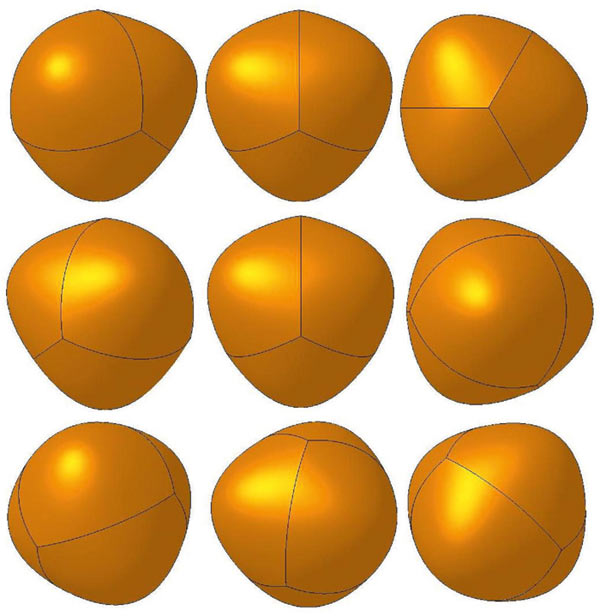
Рис. 2. Параболический тетраэдр. Виды
Параболический тетраэдр, аналогично обыкновенному правильному тетраэдру, имеет три оси симметрии, которые проходят через середины скрещивающихся ребер.
Тело имеет шесть плоскостей симметрии, каждая из которых проходит через ребро и две вершины параболоидов.
Параболический тетраэдр также обладает поворотной симметрией на угол 120° — вокруг оси, соединяющей стыковую вершину и вершину параболоида. Таких осей поворота у тела четыре по числу пар вершин.
Центра симметрии параболический тетраэдр не имеет. Центр тяжести находится в точке пересечения осей параболоидов.
Одним из способов построения параболического тетраэдра является стыковка четырех усеченных параболоидов. Для построения модели был выбран именно этот способ, поскольку он самый простой. Кстати, пригодился опыт, полученный при стыковке парабол при создании трехосевого овала треопар (Чебыкин В. Трехосевые овальные кривые стабильной формы — новые геометрические фигуры. isicad.ru, май, 2018).
Параболоиды усечены так, что при их соединении в середине ребер тела отсутствует излом. В других же точках ребер излом есть, и он незначительно увеличивается по мере приближения к стыковым вершинам. Разумеется, получить абсолютно гладкую форму тела не получится ни при каких условиях. Следует также заметить, что двугранные углы усеченных параболоидов равны 120°, а углы отсечения равны ½ (arccos(1/3)), что обеспечивает их беззазорную стыковку.
Формулы для определения площади поверхности и объема параболического тетраэдра:
 ;
;
 ,
,
где: S — площадь поверхности тела;
p — фокальный параметр параболы;
V — объем тела.
На рис. 2 показаны стандартные виды параболического тетраэдра.
Параболический тетраэдр своей формой очень похож на спутник Сатурна Янус (рис. 3).

Рис. 3. Спутник Сатурна Янус. Фото с МКА Кассини 2009 год
Дата разработки: 24.07.2018.
Программное обеспечение:
КОМПАС3D.



