Еще раз о параболических тетраэдрах

Виктор Чебыкин

Описанный в статье «Параболический тетраэдр — новое геомет­рическое тело» (САПР и графика, № 8’2018) тетраэдр оказался не единственным тетраэдром, который можно создать из параболоидов. Но поскольку он несколько отличается от других, предлагается к его названию добавить слово «большой» — «Большой параболический тетраэдр». «Почему большой»? — спросите вы.

Дело в том, что он находится на границе тетраэдров и тел, не являющихся таковыми. Расстояние h от вершин усеченных параболоидов, образующих этот тетраэдр, до точки пересечения их осей равно двум фокальным параметрам базовой параболы. При расстоянии, большем, чем 2p, получаемые тела будут иметь участки с отрицательной кривизной, что не позволяет считать их тетраэдрами. Если же это расстояние меньше 2p, все получаемые тела — тетраэдры, которых насчитывается бесчисленное множество. Понятно, что их размеры будут меньше, чем у Большого параболического тетраэдра при одном и том же параметре. Кроме того, он отлича­ется от других наиболее гладкой формой, доминантными вершинами параболоидов и едва заметными стыковыми вершинами, что также оправдывает присвоение ему персонального имени.

На рис. 1 изображен Большой параболический тетраэдр с обновленным названием.

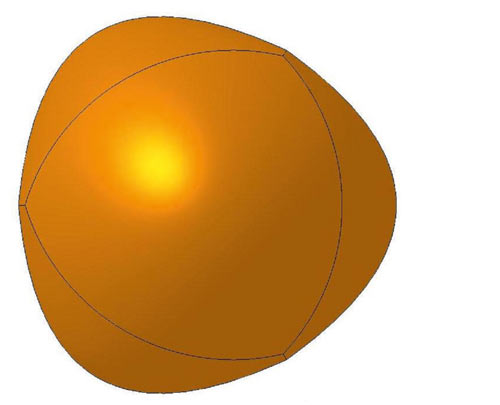
Рис. 1. Большой параболический тетраэдр

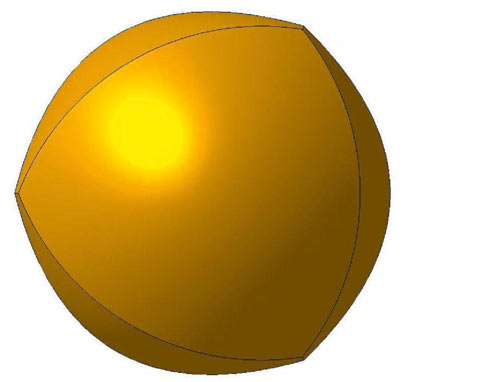
Рис. 2. Параболический тетраэдр h = 1,2p

А теперь рассмотрим несколько параболических тетраэдров с обозначенным размером, меньшим 2p. На рис. 2 изображен тетраэдр с высотой усеченного параболоида h = 1,2p.

Как видим, у него более заметно обозначились ребра и стыковые вершины, а вершины параболоидов стали более пологими. При дальнейшем уменьшении размера параболоида эти процессы продолжаются. На рис. 3 изображен тетраэдр с обозначенным размером h = 0,75p.

Рис. 3. Параболический тетраэдр h = 0,75p

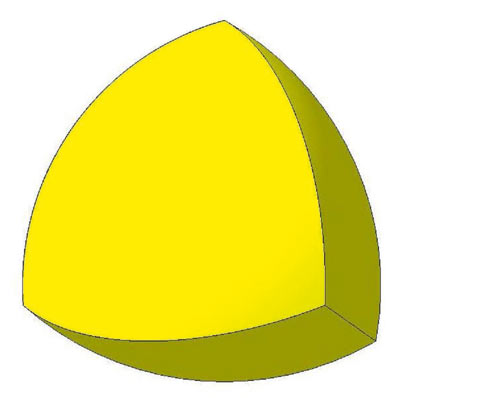
Рис. 4. Тетраэдр Рёло

Стыковые вершины этого тетраэдра уже доминируют над вершинами параболоидов, ребра явно выделены, а сам он становится похожим на тетраэдр Рёло (рис. 4).

При бесконечном уменьшении обозначенного размера параболический тетраэдр приближается по форме к обыкновенному правильному тетраэдру. По плоскостям и осям симметрии параболические тетраэдры ничем не отличаются от правильного тетраэдра (одного из тел Платона).

Немногочисленный (кадрированный) полк тетраэдров усилен ротой параболических…☺