О том, как легко мастеровому человеку мечтать с 3D-ядром

Валерий Голованёв,
инженер-аналитик и программист, г.Курган

Вступление

Мастеровыми были мой прапрадед Ефим Степанович (пахарь, бондарь и столяр), мой прадед Трифон Ефимович (пахарь и плотник) и мой дед Михаил Трифонович (кузнец, плотник, столяр, бондарь). И я мастеровой человек. Инженер и столяр­плотник­любитель.

Любому мастеровому человеку сложно... Сложно без интересных задач, сложно, когда не хватает возможностей для их реализации. В характере настоящего мастерового человека ставить перед собой порой кажущиеся мало выполнимыми задачи и их реализовывать.

Когда шесть лет назад, летом 2012 года, я вернулся к своему детищу — библиотеке проектирования тел вращения КОМПАС­Shaft (сейчас — приложение «Валы и механические передачи 3D» для КОМПАС­3D), то на печати своего ИП я изобразил пару коничек с круговым зубом. В тот момент я только мечтал о том, что когда­нибудь смогу сделать их в 3D — это был скорее некий символ. С возрастом к знакам и символам судьбы относишься более внимательно... Цель была материализована!

От червячного колеса к гипоидной передаче в КОМПАС­3D

С чего все началось? С желания! Очень хотелось дать конструктору не некие «подобия», а настоящие 3D­модели механических передач, чтобы можно было:

а) изготовить по 3D­модели зубчатое или червячное колесо, или звездочку, или коничку с круговым зубом, или (о, мечты...) гипоидную пару;

б) увидеть в 3D­сборке не условные «кракозюбры», а реальные модели;

в)  и так далее...

А почему, собственно, надо ориентироваться в механических передачах на возможности (ограничения) привычной технологии? Неправильно ущемлять конструкцию технологией. Надо делать правильные передачи с оптимальной 3D­геометрией активных рабочих поверхностей с точки зрения эксплуатации, а технология должна обеспечивать их изготовление. И такая технология, названная аддитивной, уже есть! Современные промышленные 3D­принтеры позволяют печатать металлом вполне нагруженные изделия, и эксперименты заходят довольно далеко: уже скоро созданные аддитивным способом детали станут обычным явлением в машиностроительном изделии, если не в массовом, то в мелкосерийном — точно.

Владимир Панченко,
руководитель дивизиона
«Приложения КОМПАС-3D», АСКОН

К использованию ядра в приложении «Валы и механические передачи» подтолкнул отзыв «Казцинкмаша». Для меня было очевидно, что строить можно быстрее — оставалось только убедить в этом Валерия Голованёва. Отягчающим обстоятельством было то, что Валерий не любил C++, а использовать функции C3D в контексте КОМПАС­3D можно только на этом языке программирования. Пришлось делать макет — спасибо Алексею Султанову.

Простой перевод кода в лоб сразу дал ощутимый выигрыш по скорости: точная модель зуба червячного колеса построилась за 10 секунд. Червячное колесо строилось на API около часа.

Ну а дальше мастерство Валерия позволило создавать и конички с круговым зубом.

Вот так мы подняли проект «Валы и механические передачи» на совершенно новый уровень.

Что быстрее — API КОМПАС­3D или C3D? Вопрос звучит парадоксально. C3D — это же геометрическое ядро КОМПАС­3D! Как работает ядро, так работает и КОМПАС­3D. Но при ближайшем рассмотрении, особенно в контексте прикладного разработчика, все встает на свои места.
Стандартная схема для разработчика выглядит так. Вызов функции API КОМПАС­3D приводит к добавлению объекта в модель документа, а дальше для создания геометрии идет обращение к C3D. Потом по цепочке, в обратном порядке, данные возвращаются назад в API, и вот в руках разработчика интерфейс созданного объекта.
При этом на каждом шаге с данными что­то происходит: в API их пакуют в COM, в модели документа проверяют на правильность в текущем контексте, добавляют атрибуты и данные по отрисовке. Конечно, все эти действия оптимизированы и занимают очень мало времени. Если разработчику нужно получить цилиндрическую ступень вала, то он создает эскиз и операцию выдавливания в КОМПАС­3D — всего два объекта и два обращения по цепочке. Но ситуация в корне меняется в случае с геометрией для конической передачи с круговым зубом. Для этого нужно создать множество вспомогательных кривых, поверхностей (и все это не аналитические цилиндры и конусы, а NURBS’ы), их пересечений. Прокачивание данных начинает занимать уже существенное время. Ядро при этом будет в основном простаивать. Чтобы избежать временных потерь, взаимодействие с API и моделью документа сводится к минимуму — добавь операцию с телом и прими тело, которое смоделировано в C3D. Получаем один заход в C3D и оптимально на стеке создаем всю вспомогательную геометрию, пересекаем, что нужно, и получаем результат. Работает только ядро, причем работает очень быстро!

Прошло примерно три года, и весной 2015­го я решился сделать средствами API КОМПАС настоящее червячное колесо. Принцип реализации в этой задаче мне был понятен давно: необходимо заметание инструментом тела заготовки, то есть имитация механообработки в КОМПАС­3D. Не скажу, что это было легко. Делать вырез набором из многочисленных положений инструмента неверно и долго. Необходимо сформировать совокупность поверхностей положений инструмента и создать по ним огибающую поверхность выреза. Что в общем­то и получилось, но работало очень медленно. Кроме того, необходимо было добавить реализма в процесс, то есть учесть допуски при формировании 3D­геометрии. В общем, решив одну задачу, захотелось большего — большей точности, измерений зуба червячного колеса и формирования выносок в чертежах с профилем этого зуба (а вдруг технологи­инструментальщики захотят сделать измерительные шаблоны?). Кстати, в том же году на заводе «Казцинкмаш» по моим моделям изготовили две пары червячных колес, которые были успешно поставлены в рабочие узлы и получили положительный отзыв (рис. 1 и 2).

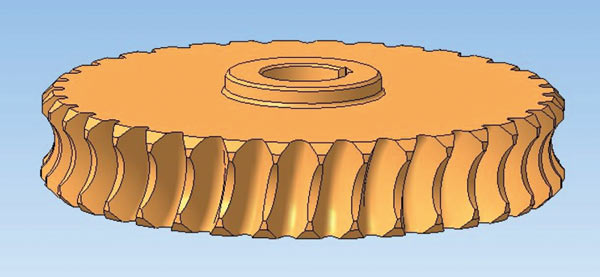
Рис. 1

Рис. 2

Идем дальше! Осенью 2015 года с подачи (или с пинка) Владимира Панченко, руководителя подразделения «Приложения КОМПАС­3D», и под опекой Алексея Султанова я начал изучать программирование на ядре C3D, на математике которого построен КОМПАС­3D. Цель — получить свободу! И я ее получил. Меня больше не ограничивало количество выполняемых операций и процедур. Все происходило достаточно быстро. На выходе я имел тело — массив вырезов из заготовки червячного колеса. Ну а дальше все просто: булева операция — и червячное колесо готово.

Затем последовали цилиндрички внешнего зацепления. Казалось бы, просто, а между тем в случае с косозубым колесом и операцией выреза по винту в КОМПАС­3D на API всё тоже строилось достаточно долго. Сейчас эти шестерни могут быть сформированы и с настоящей затыловкой.

Ну и в конце 2015 года стартовал процесс работы над коничками с круговым зубом.

Алгоритм к тому времени был проработан на API КОМПАС. Первые модели с не очень хорошей геометрией формировались до суток чистого времени. Здесь одним заметанием поверхностей не обошлось. Создавались обкатные конические передачи, и необходимо было сформировать колесо, обработав его прототипом зуборезной головки. Потом по полученной 3D­геометрии требовалось сформировать и сохранить прототип инструмента для шестерни, со всего этого снять контролируемые размеры и передать в чертеж. Далее уже на шестерне, учитывая, что она получалась идеально обкатная, нужно было локализовать контакт, то есть обеспечить правильное положение и размер пятна контакта в передаче.

Сложная и очень интересная задача. Изредка и Николай Голованов со своей командой правил по моим замечаниям функционал C3D. Таким образом, мои конички оказались еще и хорошим тестом для ядра.

Конички по моим моделям изготавливались неоднократно на разных предприятиях и работают в реальных узлах. Отработан алгоритм локализации (рис. 3 и 4).

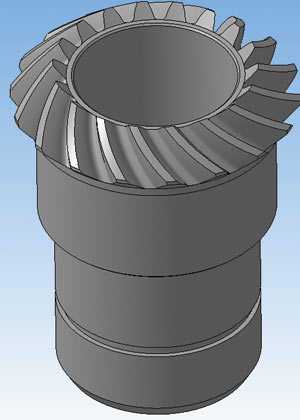
Рис. 3

Рис. 4

Но трудно было остановиться и на этом. Не устраивала меня такая локализация. Слишком сложно было ее обеспечивать. И уже весной 2018 года пришла мысль о более «прос­том» способе локализации. Собственно, идея не моя, я подсмотрел ее в материалах фирмы Klingelnberg — у них это называется profile and lengthwise crowning (рис. 5).

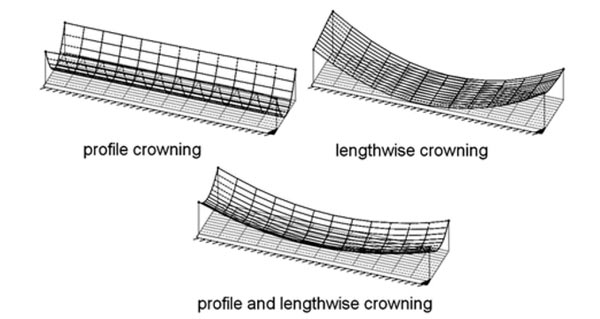
Рис. 5

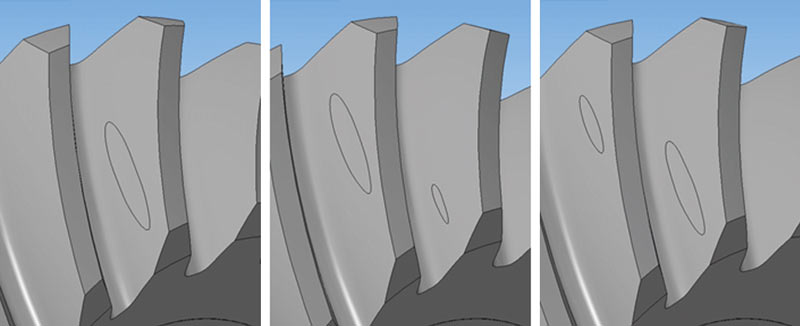
Рис. 6

Я это назвал «сделать зуб с холмиком», что и получилось. В каждом сечении профиля выреза был сделан его пересчет, и холмик удался. Коэффициенты локализации стали более простыми и понятными (рис. 6).

Николай Голованов,
руководитель разработки C3D Labs

Некоторые приложения системы КОМПАС­3D, в том числе и приложение «Валы и механические передачи 3D», работают напрямую с геометрическим ядром C3D. Это позволяет разработчикам приложений более гибко подойти к решению своих задач за счет расширения функционала (работы с низкоуровневыми функциями) и приемов построения геометрических объектов.

Если вы пишете приложение для КОМПАС­3D и хотите использовать возможности C3D напрямую, имеет смысл обращаться к ядру, встроенному в сам КОМПАС­3D. У этого способа есть единственное ограничение: надо использовать только C++, так как именно на этом языке написан сам КОМПАС. Если же вы решили работать с отдельной копией ядра внутри собственного приложения, то вам будут доступны и C#, и, в некоторых случаях, JavaScript.

Кратко о результате: пятно контакта, а это совокупность мгновенных площадок контакта на зубе шестерни за один цикл ее поворота (360/число зубьев шестерни), теперь всегда находится по середине активной поверхности зуба (на вершине «холмика»), его размер составляет более 60% всей поверхности.

Это дает следующие преимущества:

• передачи будут более долговечными и надежными;
• снизится шум в передаче;
• передача будет менее чувствительна к погрешностям монтажа.

Изготовить их, правда, пока получится только на ЧПУ, но в будущем подтянутся и аддитивные технологии.

Ну и под занавес... В этом году реализована передача­мечта, моя самая сложная на сегодня мечта­задача — гипоидные передачи. Сделать для этого пришлось очень много... Шесть лет пути после возвращения к разработке САПР. Хотя на самом деле путь начался еще в 1991 году с заказного проекта по созданию ПО для расчета конических передач с круговым зубом (рис. 7).

Рис. 7

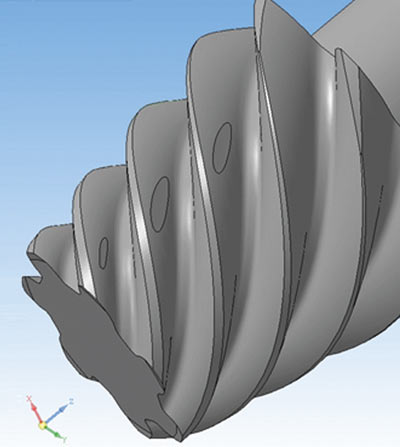
Рис. 8

Естественно, что зуб «холмиком» реализован и в них (рис. 8).

Как работает 3D­ядро в моделировании механических передач

Из функционала ядра используются самые обычные операции: создать плоскость, построить эскиз/поверхность/пересечение поверхностей и т.д.

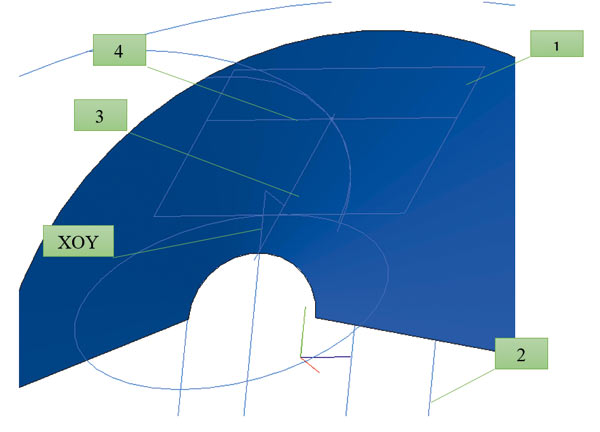
Рис. 9

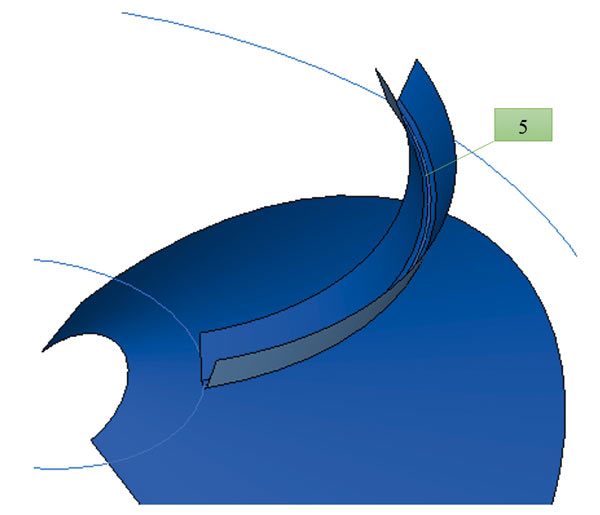
Рис. 10

Рис. 11

Рис. 12

Для примера рассмотрим последовательность операций, необходимых для формирования 3D­модели выреза конического колеса с круговыми зубьями (именно колеса, а не шестерни):

1. Формируем поверхности конусов — делительного конуса, конуса вершин и конуса впадин. Для этого на соответствующих расчетных расстояниях создаются плоскости и на них строятся эскизы окружностей расчетных диаметров, а уже по ним — конусы.
2. Строим точки центров делительного конуса и конуса впадин.
3. Далее формируются касательная плоскость к конусу впадин (1) и плоскость по средней точке колеса во впадине (2). По пересечению плоскости (1) и плоскости XOY формируется ось пересечения (3), а по пересечению плоскости (2) и плоскости (1) формируется ось пересечения (4).
4. На пересечении этих осей будет точка, через которую проходит вершина зуборезной головки (рис. 9).
5. От этой точки, зная средний угол наклона зубьев (как раз в этой точке), мы рассчитываем центр зуборезной головки.
6. Проекции полудуги зуборезной головки на конусы впадин (5) и делительный конус будут нашими направляющими. На этой направляющей (5) и будет построена базовая поверхность выреза (лофт по трем сечениям с расчетным профилем зуборезной головки) — рис. 10.
7. Далее, имея процедуру для выполнения подобной операции под разными углами качания зуборезной головки при обработке колеса, мы получаем массив поверхностей вырезов (6) — рис. 11.
8. После этого в достаточном количестве сечений (не менее 20) в нормальных плоскостях к направляющей (проекция полудуги зуборезной головки на делительный конус) будут получены совокупности линий пересечений массива поверхностей (рис. 12).
9.  Математическая обработка полученной совокупности линий пересечения позволит получить их огибающую, которая и будет одним из сечений реального выреза зуба колеса (рис. 13).
10.  По совокупности этих сечений вырезов и будет построен окончательный лофт — вырез зуба колеса (рис. 14­16).
11. С полученной геометрии будут автоматически сняты (построен зуб, секущей плоскостью сделано сечение и по нему посчитано) контрольные размеры, сам профиль зуба, и все это передано в чертеж (рис. 17 и 18).
12.  Всё достаточно просто, правда, в этом конкретном случае и без рассмотрения «небольших» скрытых от глаз читателей нюансов математических расчетов.

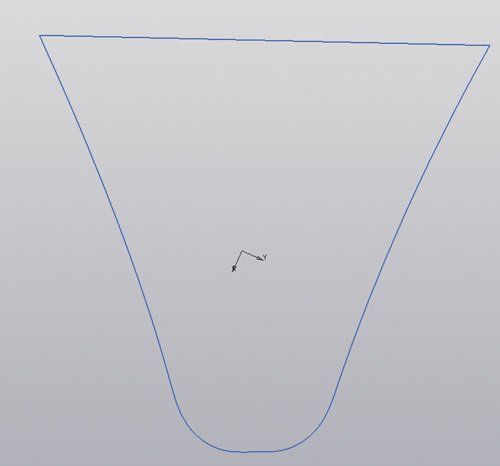
Рис. 13

Рис. 14

Рис. 15

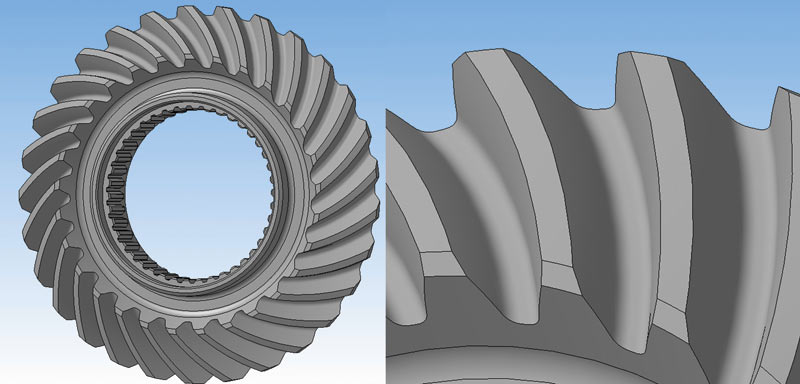
Рис. 16

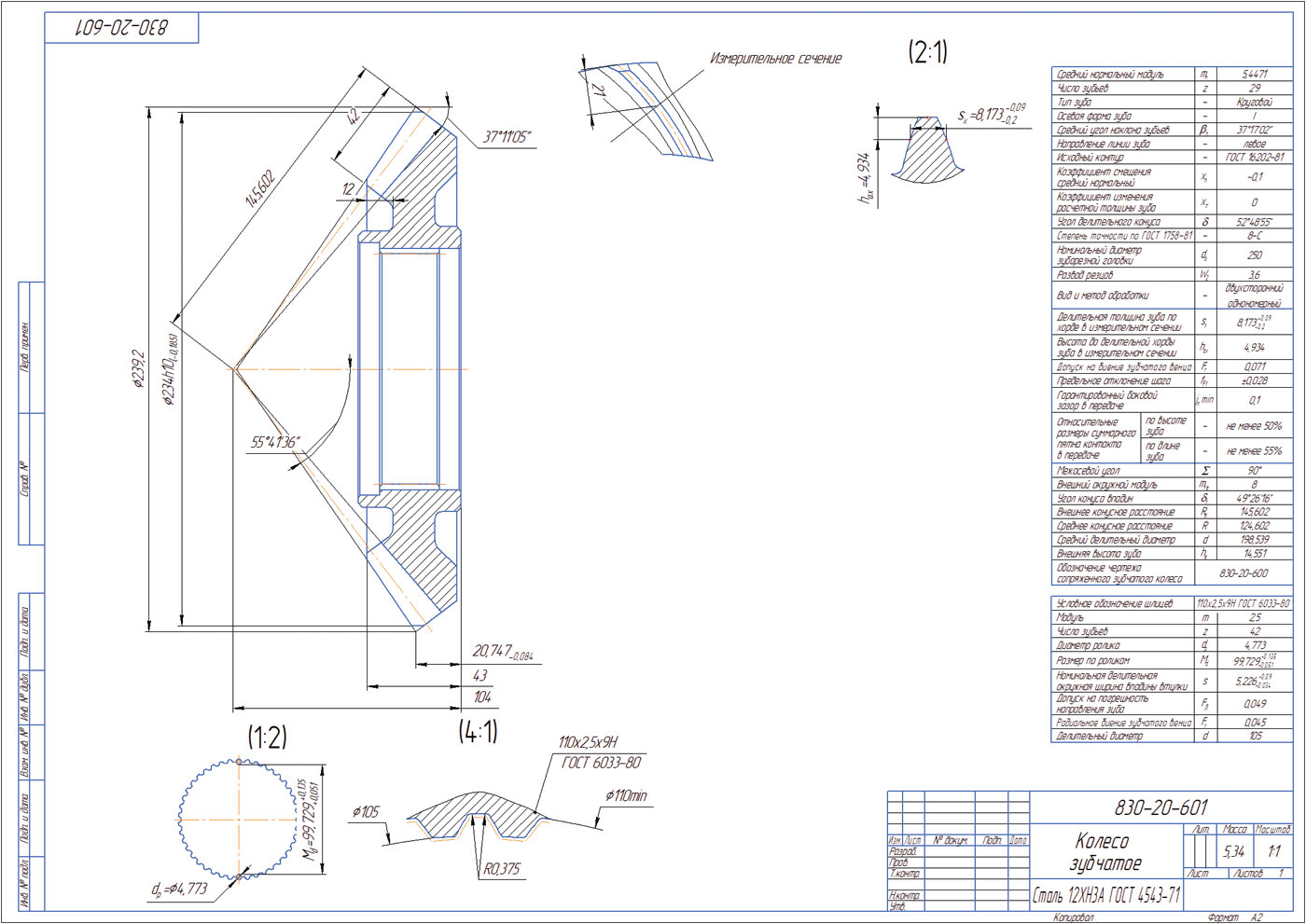
Рис. 17

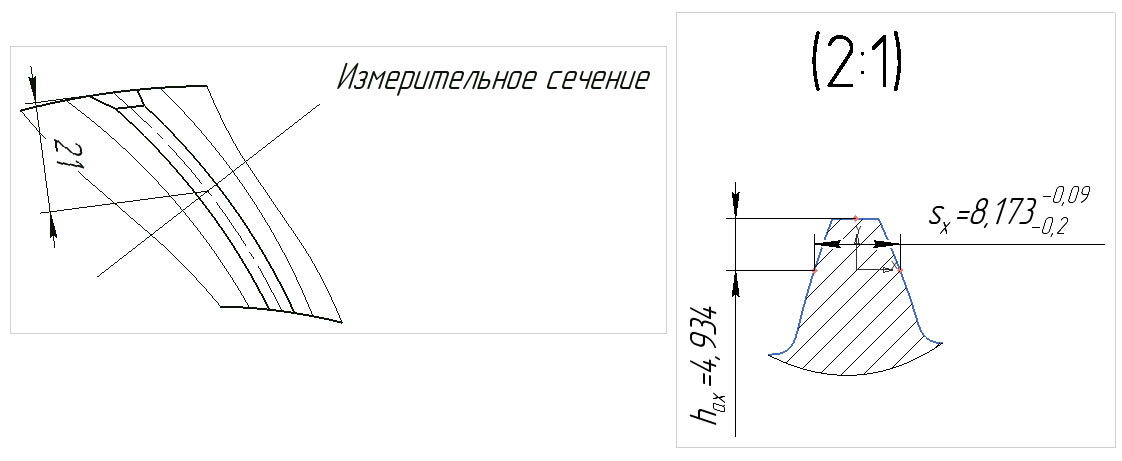
Рис. 18

Что необходимо еще мастеровому в данном случае? Пространственное воображение, фантазия и умение мечтать, в конце концов!