В данной работе предложены к рассмотрению геометрические тела — аналоги тел Платона, отличающиеся от последних криволинейными основаниями. Большинство из них, по предположению автора, показаны и описаны впервые.
Существуют ли такие геометрические тела? Да, существуют: это тетраэдр Рёло, а также параболические тетраэдры, описанные в предыдущих номерах журнала «САПР и графика» [1, 2]. Отличаясь от тел Платона криволинейными основаниями, они сохраняют все свойства симметрии, которые присущи правильным многогранникам.
Поскольку речь пойдет об аналогах всех тел Платона, нельзя обойтись без первого (не считая тетраэдра Рёло) из них — Большого параболического тетраэдра (рис. 1).
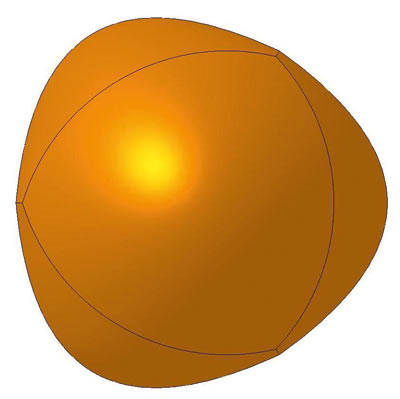
Рис. 1. Большой параболический тетраэдр
Напомню, что высота усеченных параболоидов, из которых состоит Большой параболический тетраэдр, равна двум фокальным параметрам базовой параболы. Понятно, что если высота этих параболоидов будет меньше, то и сами тетраэдры будут меньше, но при этом останутся правильными телами.
Перед тем как перейти к построению других параболических аналогов, были определены значения высот усеченных параболоидов для гексаэдра, октаэдра, додекаэдра и икосаэдра. Они соответственно равны: 1,5p; 1,25p; ≈1,191p; ≈1,071p.
На рис. 2 и 3 изображены: Большой параболический гексаэдр и Большой параболический октаэдр.
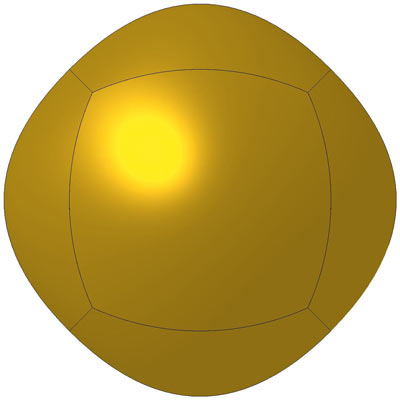
Рис. 2. Большой параболический гексаэдр
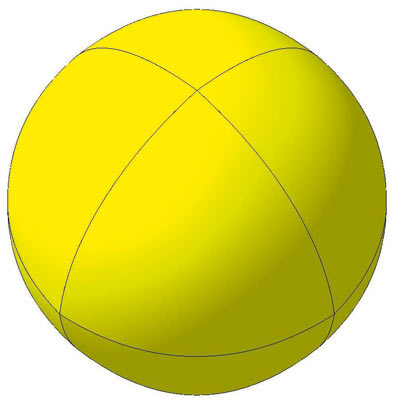
Рис. 3. Большой параболический октаэдр
Если на гексаэдре вершины параболоидов хорошо видны, то на октаэдре они практически неразличимы и тело можно принять за шар. Аналогично будут выглядеть параболические додекаэдр и икосаэдр, которые можно будет идентифицировать только по количеству оснований, ребер и стыковых вершин.
Но если в качестве оснований использовать не параболоиды, а, например, овалоиды вращения овала «циклон» [3], то на полученных телах вершины овалоидов будут прекрасно видны. Это связано с тем, что привершинные участки овала «циклон», в отличие от аналогичных участков параболы, сильно отличаются по форме от окружности. На рис. 46 изображены тела, созданные из овалоидов вращения циклона.
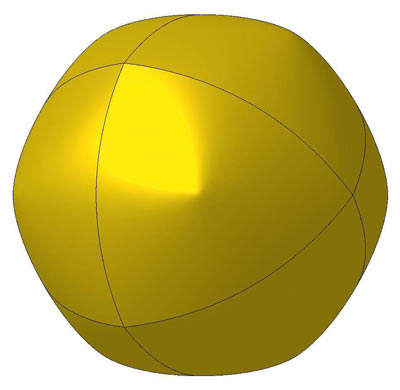
Рис. 4. Большой циклон-октаэдр

Рис. 5. Большой циклон-додекаэдр
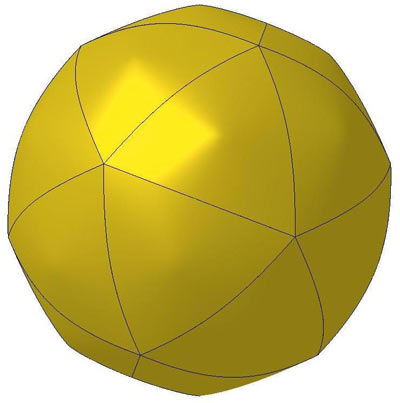
Рис. 6. Большой циклон-икосаэдр
В качестве оснований аналогов тел Платона можно использовать и овалоиды вращения других кривых. Для примера на рис. 7 и 8 показаны тетраэдр и гексаэдр, собранные из овалоидов вращения овала «фокинон» [4]. По сравнению с параболическими аналогами они имеют более развитые вершины овалоидов.
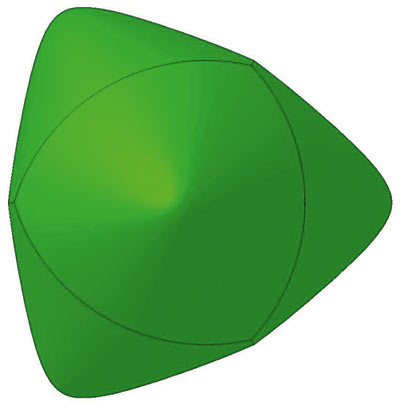
Рис. 7. Большой фокинон-тетраэдр
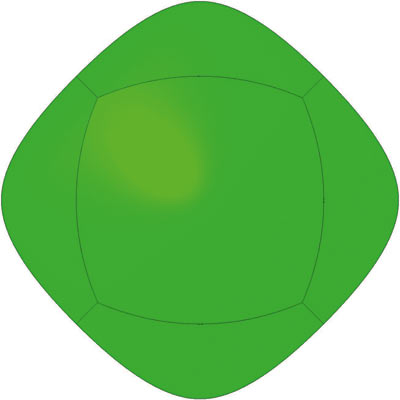
Рис. 8. Большой фокинон-гексаэдр
Что объединяет аналоги тел Платона, имеющие в названии прилагательное «большой»? Они обладают максимально возможными размерами высот усеченных овалоидов при заданных размерах базовых кривых. Кроме того, данные тела не имеют изломов в серединах ребер. Тела, состоящие из усеченных овалоидов меньших размеров (используется меньшая часть базовых кривых), имеют измененную форму, но также являются аналогами тел Платона.
Какой же вывод можно сделать на основе этого небольшого исследования?
Криволинейные аналоги у правильных многогранников (тел Платона) есть, и их много, строй — не хочу…☺
Библиографический список:
- Чебыкин В. Параболический тетраэдр — новое геометрическое тело // САПР и графика. 2018. № 8.
- Чебыкин В. Еще раз о параболических тетраэдрах // САПР и графика. 2018. № 9.
- Чебыкин В. ЦИКЛОН и ЦИТРОН — новые овальные кривые стабильной формы // isicad.ru. 2015. Сентябрь.
- Чебыкин В. Овалы стабильной формы — простейшие геометрические решатели (само и взаимо) // isicad.ru.
2016. Август.


