Сравнительный анализ ANSYS Mechanical APDL и APM Structure3D при использовании различных объемных конечных элементов

Владимир Шелофаст, д.т.н., профессор МГТУ им. Н.Э. Баумана, генеральный директор НТЦ «АПМ»

Артем Абдурашитов, к.т.н., инженер НТЦ «АПМ»

Сергей Ренев, аспирант МГТУ им. Н.Э. Баумана

Максим Венедиктов, аспирант МГТУ им. Н.Э. Баумана

В статье представлены результаты сравнительного анализа, проводимые в CAE-системах APM Structure3D и ANSYS Mechanical APDL. Целью анализа является оценка достоверности полученных значений с использованием твердотельных конечных элементов разных типов в среде APM Structure3D путем их сопоставления с эталонными, решения для которых найдены в зарубежной CAE-системе ANSYS Mechanical APDL. Анализ проводится с применением твердотельных конечных элементов первого и второго порядков при решении задач статики, геометрической нелинейности, физической нелинейности и динамики. Под динамическим анализом подразумевается модальный анализ, включающий вычисление собственных частот и собственных форм.

Наиболее эффективным методом расчета напряженно­деформированного состояния нагруженной конструкции является метод конечных элементов. Для реализации этого метода следует представить рассматриваемый объект анализа в форме, удобной для выполнения вычислительных процедур. Это означает, что реальный геометрический объект представляется в виде расчетной модели. В зависимости от конфигурации детали они могут быть смоделированы набором стержней, пластин, оболочек, твердотельных элементов и произвольной комбинацией перечисленных элементов. Все эти конечные элементы (КЭ) позволяют моделировать всю совокупность объектов, которые встречаются при проектировании. Полный набор таких КЭ имеется в отечественном программном комплексе APM Structure3D [1, 2] компании НТЦ «АПМ». Поскольку этот программный продукт представляет большой интерес на российском рынке, то оценка точности получаемых с его помощью решений позволяет оценить надежность представленного программного обеспечения и его практическую значимость. Ценность этой работы обусловлена еще и тем, что в России, хотя и не без труда, реализуется программа импортозамещения, которая предполагает использование отечественных программных продуктов в наукоемких областях, к которым, без сомнения, можно отнести и разработки CAE­систем, реализуемые в APM Structure3D.

Далее речь пойдет о расчетных моделях, которые представляют собой совокупность твердотельных КЭ различных геометрических форм. Огромное количество разных форм КЭ продиктовано многообразием возможных деталей, которые они описывают, возможностью генераторов конечно­элементной сетки и т.п. Ниже приведен перечень типов твердотельных КЭ, эффективно используемых в практике выполнения инженерных расчетов, которые будут являться предметом нашего анализа:

• тетраэдры 4­узловые;
• пирамиды 5­узловые;
• призмы 6­узловые;
• гексаэдры 8­узловые;
• тетраэдры 10­узловые;
• пирамиды 13­узловые;
• призмы 15­узловые;
• гексаэдры 20­узловые.

Для наглядности геометрическое представление различных типов КЭ показано на рис. 1.

Рис. 1. Типы твердотельных КЭ: а — тетраэдры 4-узловые;
б — пирамиды 5-узловые; в — призмы 6-узловые; г — гексаэдры 8-узловые; д — тетраэдры 10-узловые; е — пирамиды 13-узловые; ё — призмы 15-узловые; ж — гексаэдры 20-узловые

Твердотельные КЭ с количеством узлов от 4 до 8 называются элементами первого порядка, а с количеством узлов 10 и выше — второго. Это многообразие КЭ позволяет варьировать точность вычислений, размерность решаемых задач, скорость выполнения расчетов и т.п. Поскольку каждый конечный элемент содержит разное число узловых точек и различную топологию, математические методы расчета для каждого из них приводят к разной точности получаемых решений. По этой причине анализ точности вычислений выполняется по всему спектру конечных элементов.

 Учитывая обстоятельства, перечисленные выше, сформулируем цели и задачи выполняемого исследования. Первоочередной задачей является проверка адекватности результатов расчетов статической прочности и анализ динамических параметров. Под статической прочностью подразумевается определение напряженно­деформированного состояния рассматриваемого объекта, а под динамическими параметрами — модальный анализ, включающий вычисление собственных частот и собственных форм.

Корректность полученных решений можно оценить, если выполнить необходимые тестовые задачи с использованием двух независимых источников, один из которых можно считать эталонным. В нашем случае в качестве эталона применялся программный продукт ANSYS Mechanical APDL [3, 4], с результатами которого сравнивались аналогичные решения, выполненные в системе APM Structure3D.

В данной статье для всех объектов исследования использовалась сталь со следующими свойствами: модуль упругости, E = 2•105 МПа; коэффициент Пуассона, µ = 0,3; плотность,
ρ = 7800 кг/м3.

Статический линейный расчет

В качестве объекта исследования для статического расчета была выбрана прямолинейная балка длиной 1000 мм, односторонне защемленная и имеющая квадратное поперечное сечение размером 80×80 мм.

Суммарная нагрузка на балку составляет 900 Н. Нагрузка задана в виде узловых сил на противоположной от заделки грани. Направление сил противоположно оси Z глобальной системы координат. На рис. 2 приведено тетраэдральное (4­узловое) сеточное представление модели балки с заданными граничными условиями. Сеточное представление состоит из 56 770 КЭ.

Рис. 2. КЭ-модель балки из 4-узловых твердотельных КЭ

Простейшее конструктивное решение было принято потому, что в этом случае легко получить адекватное сеточное представление.

По результатам нагружения сеточной модели получены карты полей напряжений и перемещений в системе ANSYS Mechanical APDL и в системе APM Structure3D. Результаты напряженного состояния представлены на рис. 3, а перемещений на рис. 4. Анализ напряженного состояния выполнялся для случая расчета эквивалентных напряжений по Мизесу, а под перемещениями понимались величины суммарных перемещений. Как видно из сравнительного анализа, полученные в результате карты суммарных перемещений и эквивалентных напряжений адекватны как по характеру, так и по численным параметрам. Анализ адекватности результатов в системе ANSYS Mechanical APDL и в системе APM Structure3D выполнялся на одной и той же сеточной модели, а для полной надежности результатов вычислений они рассматривались покомпонентно. Сравнительные результаты вычислений напряжений и перемещений в точках с экстремальными значениями, полученные с применением тетраэдральных КЭ, приведены в табл. 1. С целью получения большей достоверности результатов анализа при расчете напряжений и перемещений не используется процедура усреднения по узлам в КЭ. Анализ результатов показал, что сравнительная точность аналогичных решений достаточно высокая.

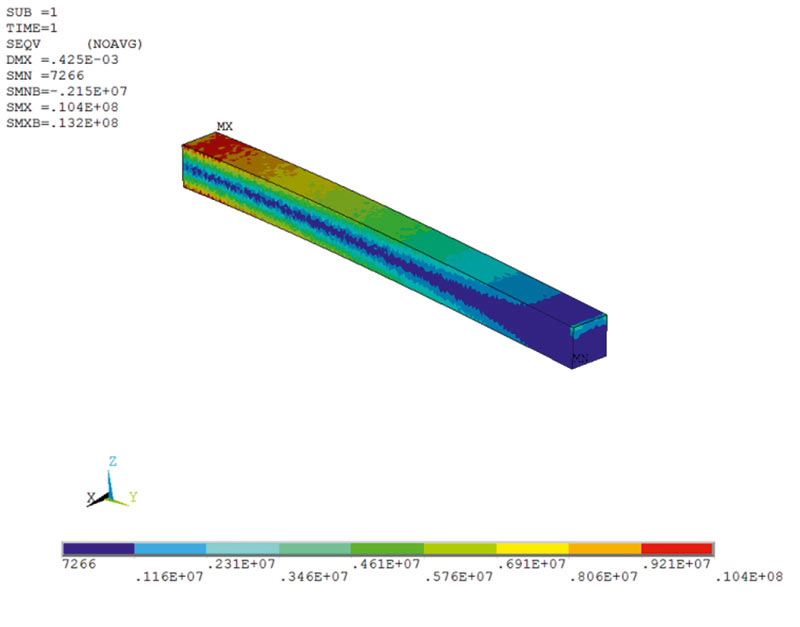
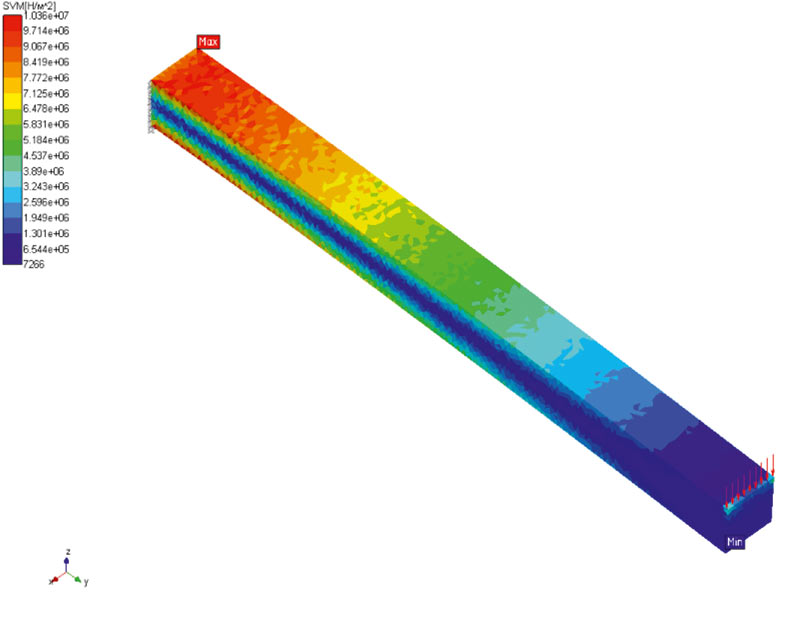
Рис. 3. Карта суммарных напряжений по Мизесу: а — ANSYS Mechanical APDL; б — APM Structure3D

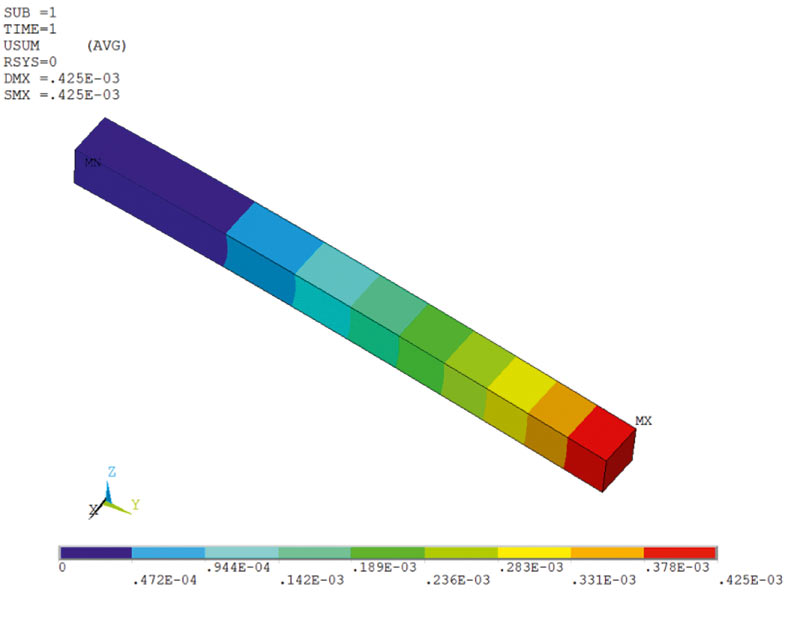
Рис. 4. Карта суммарных перемещений: а — ANSYS Mechanical APDL; б — APM Structure3D

Таблица 1. Сравнение экстремумов для различных карт результатов

Оценка достоверности получаемых решений будет неполной без сравнительных результатов анализа других заявленных типов КЭ. Следует отметить, что такие исследования были выполнены, а результаты полученных сравнительных решений по компонентам напряжений представлены в виде гистограммы на рис. 5. На этом же рисунке приведены результаты абсолютных расхождений в напряжениях, а на рис. 6 — в относительных процентных величинах.

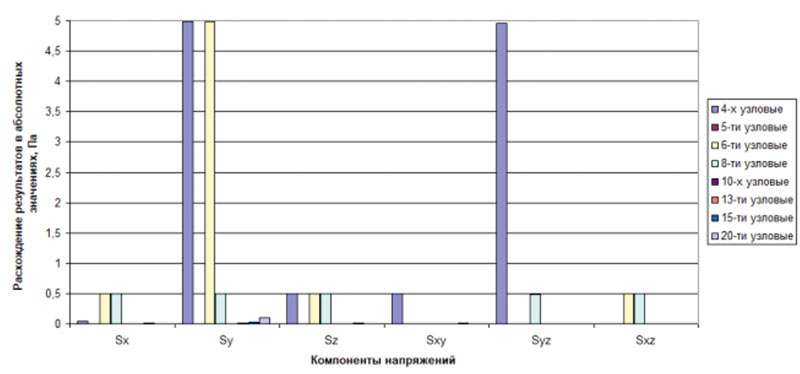
Рис. 5. Расхождение результатов в абсолютных значениях для всех твердотельных КЭ

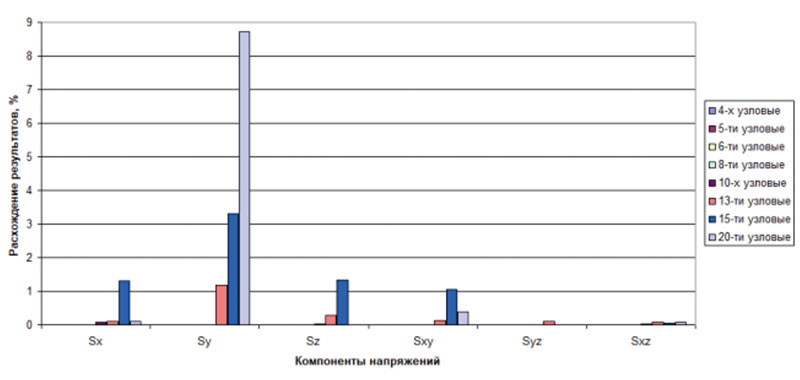
Рис. 6. Расхождение результатов в процентах для всех твердотельных КЭ

Максимальная разница результатов расчета напряжений в процентном соотношении между APM Structure3D и ANSYS Mechanical APDL составила 8,73% для 20­узловых КЭ. В абсолютных значениях данное расхождение равно 0,1011 Па.

Максимальное расхождение результатов расчета напряжений в абсолютных значениях между APM Structure3D и ANSYS Mechanical APDL составило 4,8929 Па для 4­узловых КЭ. В процентном соотношении данное расхождение не достигло 0,01%.

Следует отметить, что результаты статического расчета показали отличное качество расчетов и высокую надежность получаемых решений в системе APM Structure3D. Все эти решения получены для случая, когда материал деформируется линейно.

Расчет на геометрическую нелинейность

В случае геометрической нелинейности выполняется учет изменения деформированного состояния на результат оценки напряженно­деформированного состояния объекта анализа.

Расчет геометрической нелинейности был выполнен для балки, изображенной на рис. 7. Балка имеет длину 10 000 мм. Сечение балки — прямоугольник со сторонами 100×60 мм. Суммарная сила на балку составляет 23 240,42 Н. Нагрузка задана в виде узловых сил на противоположной от заделки грани. Направление сил противоположно оси Y глобальной системы координат.

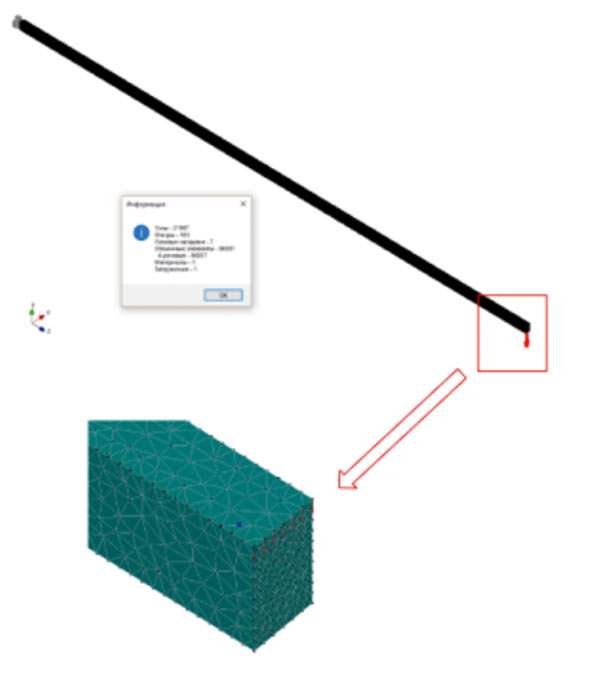
Рис. 7. КЭ-модель балки с прямоугольным сечением

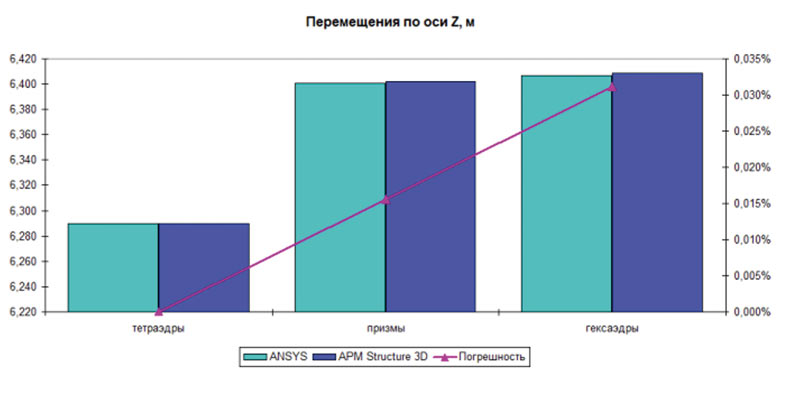
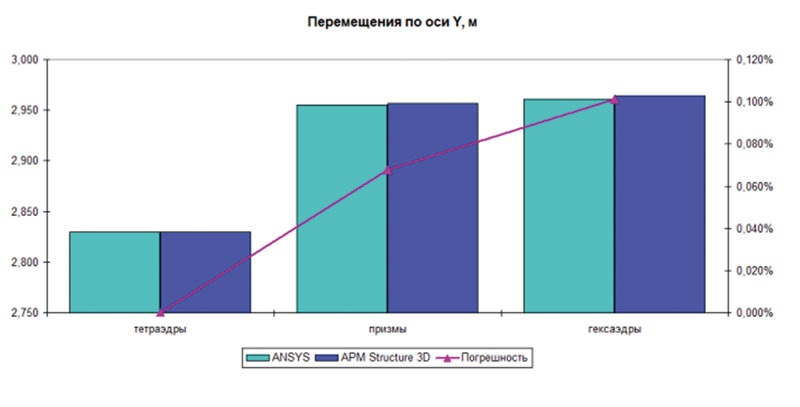
Результаты выполненных нелинейных расчетов оформлены в виде гистограмм и представлены ниже. Результаты анализа точности расчета перемещений балки в случае учета геометрической нелинейности показаны на рис. 8. Результаты определения эквивалентных напряжений по Мизесу приведены на рис. 9.

а

б

Рис. 8. Результаты геометрически нелинейного расчета:
а — перемещения по оси Z; б — перемещения по оси Y

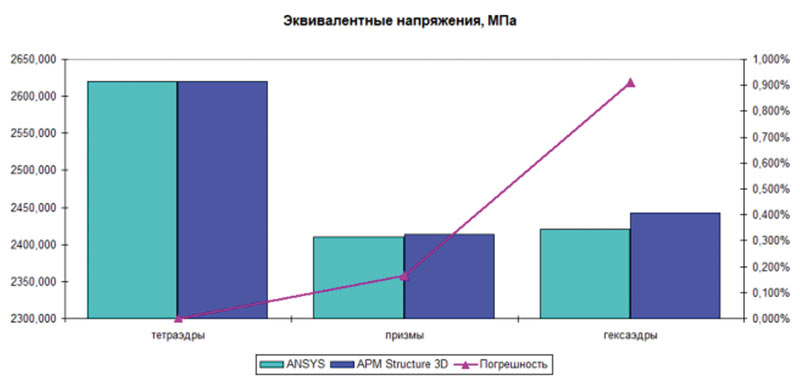
Рис. 9. Эквивалентные напряжения по Мизесу при геометрически нелинейном расчете

Расчет на физическую нелинейность

В случае физической нелинейности выполняется учет нелинейности деформационных характеристик материала объекта. Для случая расчета физической нелинейности необходимо задать диаграмму деформирования.

Анализ физической нелинейности был выполнен с использованием балки длиной 1000 мм кольцевого поперечного сечения, диаметром 80 мм и толщиной стенки трубы 10 мм, которая смоделирована гексагональными твердотельными конечными элементами. КЭ­модель балки показана на рис. 10. Диаграмма деформирования для стали приведена на рис. 11.

Рис. 10. КЭ-модель балки с кольцевым поперечным сечением:
а — внутреннее давление; б — изгиб

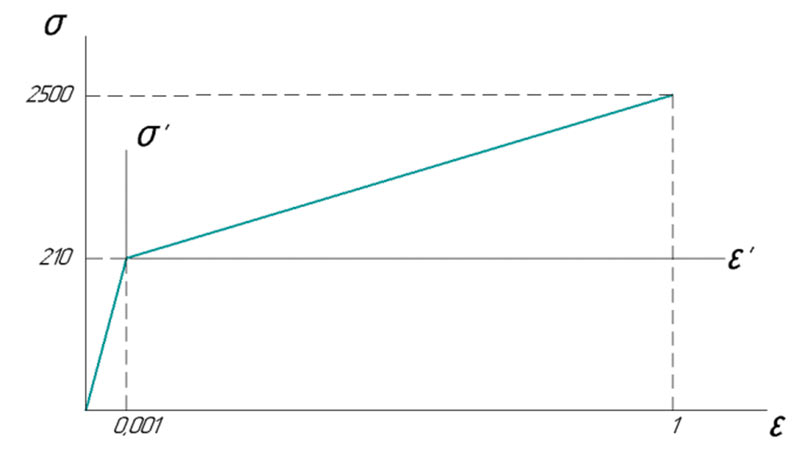
Рис. 11. Нелинейная характеристика поведения материала

Труба нагружена внутренним давлением 70 МПа и консольной силой 9600 Н.

Сделано это было потому, что такая постановка позволила выйти на нелинейный режим при относительно малых внешних нагрузках. Покомпонентная диаграмма напряжений для физически нелинейного расчета приведена на рис. 12.

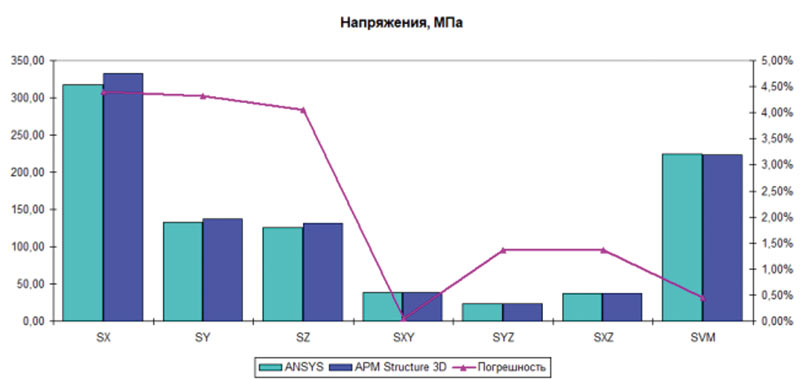
Рис. 12. Покомпонентная диаграмма напряжений для физически нелинейного расчета

Динамический расчет

Теперь рассмотрим динамическую задачу. Для твердотельных элементов выполнена проверка точности оценки собственных частот и форм. Для консольно защемленной балки прямоугольного сечения, показанной на рис. 2, результаты расчета собственных частот для тетраэдральных КЭ представлены в табл. 2. Сравнивались результаты расчета первых 30 собственных частот и форм по методу Ланцоша [5, 6, 7]. Из сравнительной оценки различий результатов численных решений в системах ANSYS Mechanical APDL и APM Structure3D следует, что они не превышают 1%. Такие результаты получены для всех рассмотренных типов КЭ, и по этой причине визуализация таблиц лишена практического смысла. Аналогичные выводы можно сделать и из сравнения собственных форм.

Таблица 2. Сравнение собственных частот балки (тетраэдры)

Статический расчет с учетом полей температур

Для сравнительного анализа результатов статического расчета с учетом полей температур использовалась КЭ­модель трубы из 6­ и 15­узловых призм. Длина трубы составляет 600 мм, внешний диаметр 30 мм и толщина 3 мм. Температура в узлах по внутренней поверхности трубы равна 323 °К. Температура в узлах по внешней поверхности трубы равна 293 °К. КЭ­модель трубы с заданными граничными условиями показана на рис. 13.

Рис. 13. КЭ-модель трубы с заданными граничными условиями

Максимальное расхождение результатов расчета напряжений с усреднением значений по узлам в APM Structure3D и ANSYS Mechanical APDL составило 17,56%. В абсолютных значениях такое расхождение равно 49 330 Па.

Показания экстремумов для карт результатов перемещений и напряжений без усреднения значений по узлам приведены в табл. 3.

Таблица 3. Сравнение экстремумов для различных карт результатов

Выводы по результатам сравнительного анализа ANSYS Mechanical APDL и APM Structure3D

Сравнительный анализ результатов статического расчета, расчета на геометрическую и физическую нелинейность для аналогичных объемных КЭ в программных комплексах APM Structure3D и ANSYS Mechanical APDL показал:

• расхождение результатов напряжений, возникающих в каждом КЭ, незначительно. Данное расхождение возникает в узлах КЭ при малых значениях напряжений, отличающихся на несколько порядков по сравнению с действующими напряжениями в остальных узлах КЭ;
• экстремальные значения компонентов напряжений и перемещений на различных картах результатов в APM Structure3D и ANSYS Mechanical APDL имеют близкие значения. Отличие экстремальных значений на картах результатов обусловлено расхождением результатов расчета в каждом КЭ.

Сравнительный анализ результатов расчета собственных частот для аналогичных объемных КЭ в программных комплексах APM Structure3D и ANSYS Mechanical APDL, показал:

• при нахождении 30 собственных частот, для различных типов объемных КЭ, результаты совпадают с малой погрешностью.

Сравнительный анализ результатов статического расчета с учетом поля температур, полученного из расчета стационарной теплопроводности, для 6­ и 15­узловых призм в программных комплексах APM Structure3D и ANSYS Mechanical APDL показал:

• расхождение результатов напряжений, возникающих в каждом КЭ, незначительно в абсолютных величинах;
• экстремальные значения компонентов напряжений и перемещений на различных картах результатов в APM Structure3D и ANSYS Mechanical APDL близки. Различие экстремальных значений для 15­узловых призм возникает на карте эквивалентных напряжений. Это связано с тем, что ANSYS Mechanical APDL строит карту только по узловым значениям, а APM Structure3D — и по промежуточным точкам.

Список использованных источников:

1. APM Structure3D. Свидетельство о государственной регистрации программы № 2014614236 от 21.04.2014 г. Аттестационный паспорт программного средства № 330 от 18.04.2013 г.
2. Замрий А.А. Проектирование и расчет методом конечных элементов в среде APM Structure3D. М.: Издательство АПМ. 2010. 376 с.
3. ANSYS Mechanical Pro Paid­Up. Аттестационный паспорт программного средства № 1066204 от 30.09.2016 г.
4. ANSYS Help Viewer. Version 17.2.0.
5. Papadrakakis, Solving large­scale problems in mechanics, John Wiley & Sons Ltd, 1993.
6. Hughes Th. J. R. The Finite Element Method. Linear Static and Dynamic. FEM Analysis.
7. Parlett B.N., 1980. The Symmetric Eigenvalue Problem. Prentice­Hall, Inc., Englewood Cliffs, N.J. 07632.