При написании предыдущей статьи (http://isicad.ru/ru/articles.php?article_num=20307) я раздумывал, как назвать тела, ограниченные овалоидными поверхностями. А назвать их лучше было овалоидными полиэдрами. Следовательно, тела, ограниченные коническими поверхностями, следует назвать коническими полиэдрами.
Если плоские основания правильных многогранников (тел Платона) заменить на поверхности прямых круговых конусов, то, при определенных параметрах конусов и их взаимного расположения, можно получить правильные конические полиэдры. После того как была построена модель первого такого тела — конического тетраэдра, я предпринял попытку найти в Интернете нечто подобное и… ничего не нашел, что, конечно, удивило. Поскольку поиск проводился недолго, примерно по полчаса в Google и Яндексе, выводов об отсутствии или существовании таких геометрических форм делать, пожалуй, не стоит. Нет ничего страшного в том, что, возможно, будут повторены чьито исследования, более того — могут быть выявлены новые свойства этих тел.
Правильный конический тетраэдр
Рис. 1. Правильный конический тетраэдр
Элементы: основания конические — 4; вершины стыковые — 4; ребра гиперболические — 6.
Параметры:
угол конуса 2α = arccos(1/3);
угол между осями конусов β = arccos(–1/3).
Формулы площади поверхности и объема:
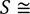5,469 h2;
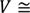1,058 h3,
где S — площадь поверхности тела;
V — объем тела;
h — расстояние от центра тела до вершины конуса.
Замечательная константа: отношение расстояния от центра тела до вершины конуса к расстоянию от центра до стыковой вершины равно 5/3.
Правильный конический гексаэдр
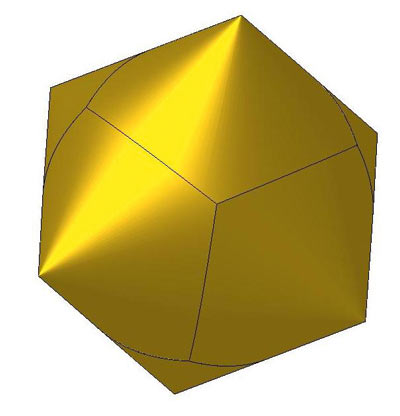
Рис. 2. Правильный конический гексаэдр
Элементы: основания конические — 6; вершины стыковые — 8; ребра гиперболические — 12.
Параметры:
угол конуса 2α = arccos(0);
угол между осями конусов β = arccos(0).
Формулы площади поверхности и объема:
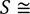7,432 h2;
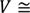1,752 h3.
Правильный конический октаэдр
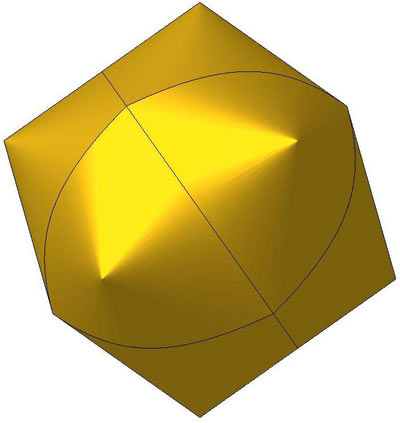
Рис. 3. Правильный конический октаэдр
Элементы: основания конические — 8; вершины стыковые — 6; ребра гиперболические — 12.
Параметры:
угол конуса 2α = arccos(–1/3);
угол между осями конусов β = arccos(1/3).
Формулы площади поверхности и объема:
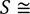9,129 h2;
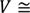2,485 h3.
Правильный конический додекаэдр
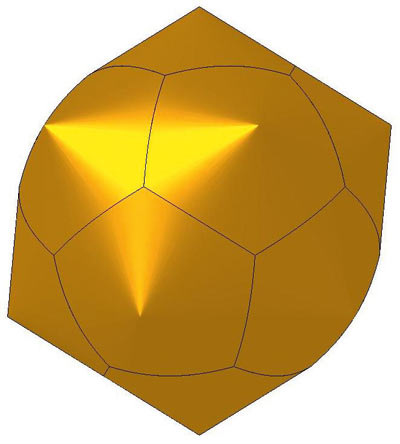
Элементы: основания конические — 12; вершины стыковые — 20; ребра гиперболические — 30.
Параметры:
угол конуса 2α = arccos(–(√5)/5);
угол между осями конусов β = arccos((√5)/5).
Формулы площади поверхности и объема:
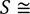9,811 h2;
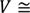2,782 h3.
Правильный конический икосаэдр
Рис. 5. Правильный конический икосаэдр
Элементы: основания конические — 20; вершины стыковые — 12; ребра гиперболические — 30.
Параметры:
угол конуса 2α = arccos(–(√5)/3);
угол между осями конусов β = arccos((√5)/3).
Формулы площади поверхности и объема:
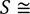11,297 h2;
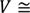3,518 h3.
***
Некоторые общие свойства правильных конических полиэдров:
- все эти геометрические тела выпуклые;
- свойства симметрии тел полностью совпадают с аналогичными свойствами соответствующих правильных многогранников (тел Платона);
- доминантными вершинами тел являются вершины конусов;
- прямая, соединяющая вершины соседних конусов, проходит через середину ребра, разделяющего поверхности этих конусов.
