Анализ статической прочности и жесткости поворотного кулака электромобиля BravoEgo

Владимир Бегеев,
студент, ФГБОУ ВО «Национальный исследовательский Мордовский государственный университет им. Н.П. Огарёва», Рузаевский институт машиностроения (филиал), г.Саранск

Сергей Ефанов, к.т.н., доцент кафедры конструкторско-технологической информатики, ФГБОУ ВО «Национальный исследовательский Мордовский государственный университет им. Н.П. Огарёва», Рузаевский институт машиностроения (филиал), г.Саранск

В современном мире все большей популярностью пользуются электромобили. По сравнению с автомобилями, использующими двигатель внутреннего сгорания, они имеют ряд неоспоримых преимуществ: высокий КПД; сравнительная простота техобслуживания; менее вредное воздействие на окружающую природу и т.д.

В связи с этим очень актуальными являются вопросы проектирования и анализа напряженно­деформированного состояния [1, 2, 3] как всей машины, так и различных узлов в отдельности.

В данной работе рассмотрен анализ поворотного кулака (рис. 1), входящего в передний подвес электромобиля BravoEgo.

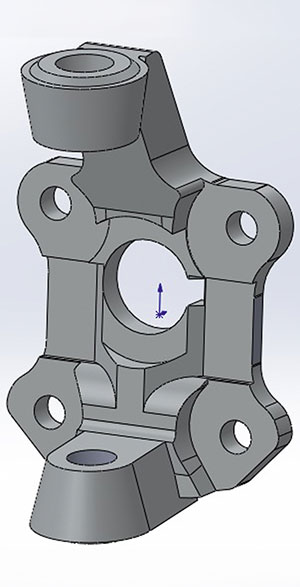
Рис. 1. 3D-модель поворотного кулака

Подвеска в автомобиле предназначена для смягчения или гашения возникающих при движении транспорта по неровной дороге колебаний, передающихся кузову автомобиля. Также подвеска предназначена для соединения кузова и колес таким образом, что колеса могут менять свое расположение независимо от кузова, регулируя направление движения автомобиля. 3D­модель переднего подвеса правого колеса представлена на рис. 2.

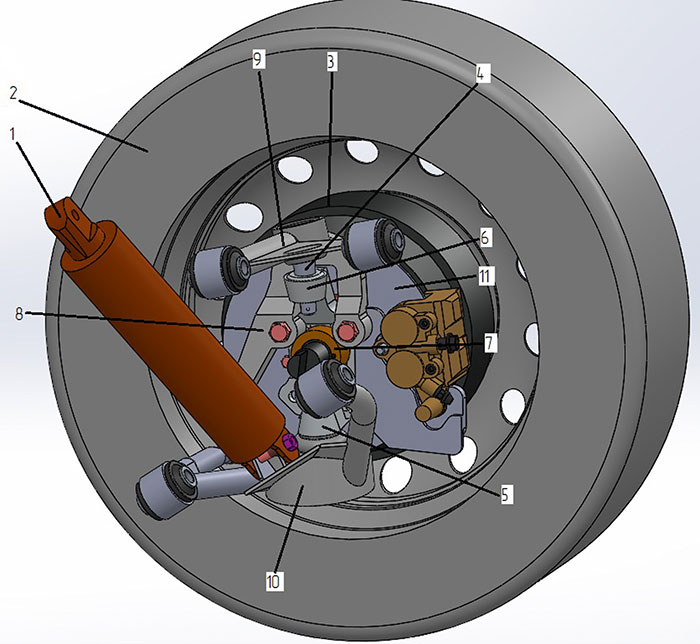
Рис. 2. 3D-модель переднего подвеса правого колеса:
1 — амортизатор; 2 — колесо; 3 — мотор-колесо;
4 — палец шаровой верхний; 5 — палец шаровой нижний; 6 — поворотный кулак; 7 — проставка кулака; 8 — рулевая сошка; 9 — рычаг верхний; 10 — рычаг нижний;
11 — тормозной диск

Одна из основных задач, решаемых в процессе создания 3D­модели силовой конструкции, состоит в адаптации сборки к последующему конечно­элементному анализу [4]. Модель должна обеспечивать адекватность получаемых результатов, но при этом быть экономичной в плане вычислительных затрат.

Поэтому расчетная схема будет состоять из поворотного кулака, верхнего и нижнего пальцев шаровых, передающих нагрузку на исследуемую деталь, и проставки кулака, предназначенного для увеличения жесткости кулака. Рассчитываемая 3D­модель (сборка) построена в программном комплексе SOLIDWORKS и представлена на рис. 3.

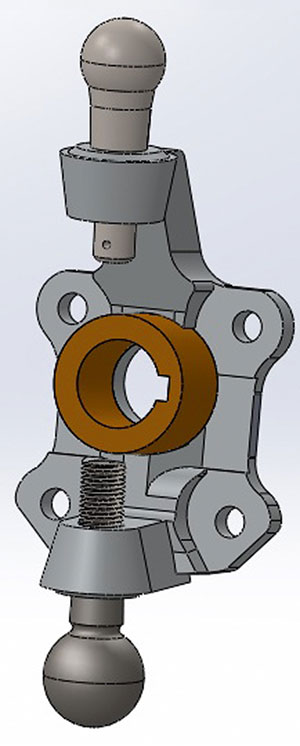
Рис. 3. Рассчитываемая 3D-модель

Важнейшим элементом модели являются граничные условия. Современные CAE­системы позволяют задавать различные виды граничных условий: граничные условия по перемещениям, то есть связи; граничные условия по внешним воздействиям (сосредоточенные и распределенные силы); граничные условия, связанные с контактным взаимодействием тел [4, 5]. Для адекватного поведения рассчитываемой модели нами были заданы три комплекта контактов. Один комплект, называемый «Нет проникновения», — между поворотным кулаком и проставкой кулака. И два комплекта, называемые «Связанные», — между поворотным кулаком и верхним и нижним пальцами шаровой.

Также были наложены связи: на центральное отверстие поворотного кулака и проставки кулака в радиальном направлении (рис. 4а), на заднюю поверхность поворотного кулака перпендикулярно грани (рис. 4б) и на боковую поверхность шпоночного паза (рис. 4в).

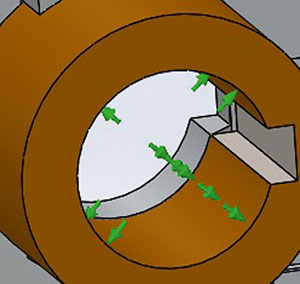
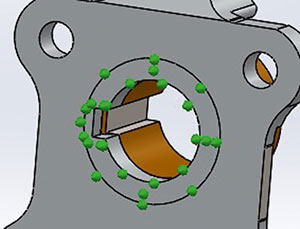
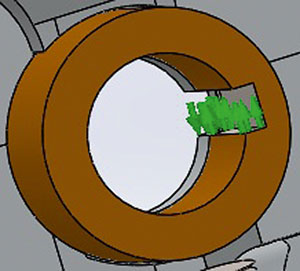
Рис. 4. Связи

Предполагается, что нагрузка на исследуемый узел передается через верхнюю и нижнюю шаровые.

Одна из важнейших процедур конечно­элементного анализа — это создание конечно­элементной сетки, или мешинг [6, 7, 8]. Мешинг производился в приложении SOLIDWORKS Simulation. Конечно­элементная модель представлена на рис. 5.

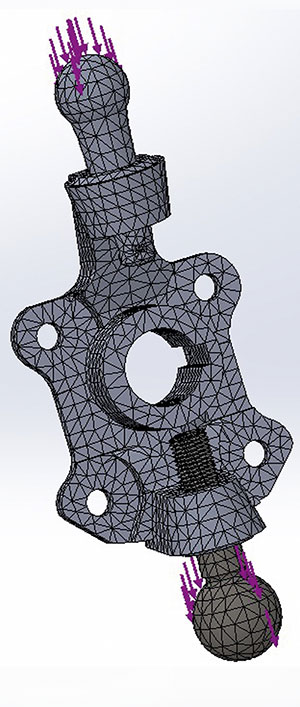
Рис. 5. Конечно-элементная модель

Результаты конечно­элементного анализа представлены в виде карты напряжений по Мизесу и не превышают 81,695 МПа (рис. 6).

Рис. 6. Эпюра напряжений по Мизису с сингулярностью

Полученный результат позволяет сделать следующий вывод: максимальное напряжение наблюдается только в одном элементе, находящемся на стыке острых кромок. Поэтому для уточнения результата и во избежание эффекта сингулярности [9] в исследуемую деталь вносятся изменения виде фасок на острые грани в области максимальных напряжений.  Полученные результаты представлены на рис. 7. Максимальные напряжения не превышают 58,954 МПа, что гораздо меньше предела текучести [10].

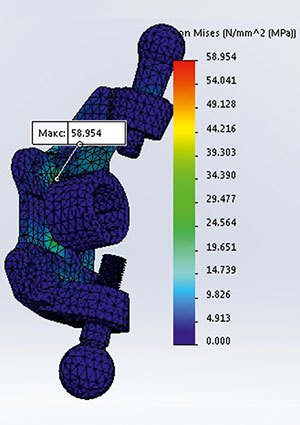
Рис. 7. Эпюра напряжений по Мизесу

Эпюра распределения коэффициента запаса прочности представлена на рис. 8. Коэффициент запаса прочности превышает 10, а для деталей, испытывающих динамические нагрузки, коэффициент запаса прочности должен быть выше 2­3. По этому показателю деталь удовлетворяет требованиям прочности.

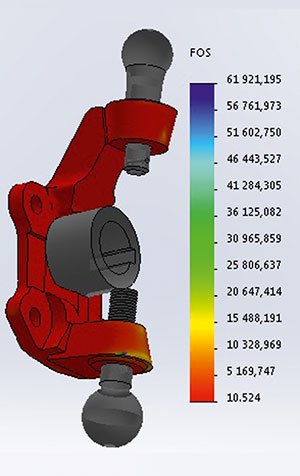
Рис. 8. Эпюра распределения коэффициента запаса прочности

Согласно техническим требованиям исследуемая деталь должна обеспечивать не менее 1 млн циклов нагружения. Был произведен анализ усталостной прочности детали. Учитывая, что нагрузка может менять свое направление, рассматривается нагружение по симметричному циклу. Полученные результаты представлены на рис. 9.

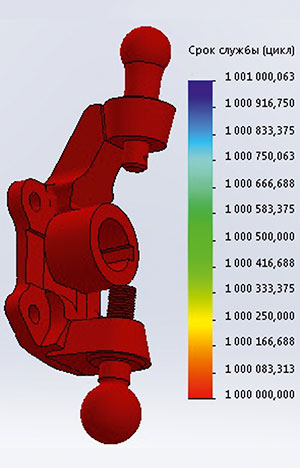
Рис. 9. Эпюр «Срок службы»

Проведенный комплекс расчетов выявил следующее:

• проанализированы максимальные значения напряжений и доказано, что максимальные напряжения не превышают предел текучести материала;
• проанализирован коэффициент запаса прочности, который значительно превышает допустимое значение;
• проведен анализ усталостной прочности детали, результат которого  доказал ее надежность.

Список использованной литературы:

1. Алямовский А.А. COSMOSWorks. Основы расчета конструкций на прочность в среде SOLIDWORKS. М.: ДМК Пресс, 2010. 784 с., ил. (серия «Проектирование»).
2. Алямовский А.А. Инженерные расчеты в SOLIDWORKS Simulation. М.: ДМК Пресс, 2010. 464 с., ил. (серия «Проектирование»).
3. Алямовский А.А. SOLIDWORKS Simulation. Как решать практические задачи. СПб.: БХВ­Петербург, 2012. 448 с.
4. Чугунов М.В., Кечемайкин В.Н., Панин М.В., Полунина И.Н., Махров Г.А. Анализ статической прочности и жесткости несущих элементов конструкции электромобиля BravoEgo // Интернет­журнал «НАУКОВЕДЕНИЕ». 2016. Т. 8. № 3. URL: http://naukovedenie.ru/PDF/134TVN316.pdf.
5. Чугунов М.В., Осыка В.В., Махров Г.А. Анализ прочности и жесткости элементов механических передач в среде SOLIDWORKS на базе API. Научные труды SWorld. 2013. Т. 9. № 3. С. 33­36.
6. Кудаев С.П., Чугунов М.В., Фоминов А.Г., Борискин С.И., Курганов В.В., Кармишин А.М. Моделирование процесса сварки боковой стенки вагона зерновоза в среде SOLIDWORKS SIMULATION. Вестник Мордовского университета. 2015. Т. 25. № 1. С. 96­100.
7. Ефанов С.А. Восстановление ремонтно­технологического оборудования полимерными композиционными материалами / А.В. Котин, А.В. Конаков, С.А. Ефанов // Труды ГОСНИТИ. 2014. Т. 117. С.186­190.
8. Котин А.В. Компьютерное моделирование функционирования восстановленного соединения «подшипник­корпус» шпиндельного узла полимерными композиционными материалами / Котин А.В., Ефанов С.А. // Энергоэффективные и ресурсосберегающие технологии и системы. Сборник научных трудов международной научно­практической конференции, посвященной памяти доктора технических наук профессора Ф.Х. Бурумкулова. 2016.
9. Frei W. Распознавание и разрешение сингулярностей в моделях при построении расчетной сетки / Walter Frei // Блог COMSOL электронный ресурс. 2013. https://www.comsol.ru/blogs/how­identify­resolve­singularities­model­meshing/
10. Электронный ресурс: Марочник сталей и сплавов http://www.manual­steel.ru/20.html.