
Сергей Звонов, к.т.н., доцент кафедры ОМД, Самарский национальный исследовательский университет имени академика С.П. Королева

Алексей Батурин, магистрант группы 1139, лаборант, Самарский национальный исследовательский университет имени академика С.П. Королева

Роман Уперчук, студент группы 1408, Самарский национальный исследовательский университет имени академика С.П. Королева
Процесс прессования алюминиевых профилей — широко распространенный метод обработки металлов давлением. Активное использование прессования объясняется благоприятной схемой напряженного состояния деформируемого металла — всесторонним неравномерным сжатием. Данный метод позволяет получать длинномерные изделия с толщиной стенки до 0,5 мм.
Предварительный расчет инструмента включает множество задач, таких как расчет геометрии инструмента, определение температурно-скоростного режима, расчет энергосиловых параметров. В связи с этим существует необходимость снижения временных затрат на подготовку производства. Для выполнения этой задачи активно применяются различные системы автоматизированного проектирования, например QForm — Extrusion и КОМПАС 3D. В QForm — Extrusion применяется модель Лагранжа — Эйлера для расчета установившейся стадии истечения металла. Модель Лагранжа — Эйлера основана на следующем предположении: комплект инструментов уже заполнен металлом и течение металла внутри него не изменяется. Таким образом, конечно-элементная сетка внутри комплекта инструментов представляет собой область расчета и сетка внутри области расчета не изменяется, а металл течет сквозь нее [1].
В статье описана методика расчета конструкции сплошной матрицы для изготовления тонкостенного алюминиевого профиля и приведены результаты моделирования процесса прямого прессования в программном комплексе для оптимизации процессов обработки металлов давлением QForm VX.
В качестве примера для расчета используется тонкостенный профиль из алюминиевого сплава АД31 (рис. 1). Исходные данные для расчета: геометрические размеры поперечного сечения, площадь поперечного сечения, теоретическая масса, диаметр описанной окружности, наружный периметр профиля, температуры заготовки и инструмента. Оборудование — пресс усилием 1320 тс. Диаметр контейнера 150 мм. Метод прессования прямой.
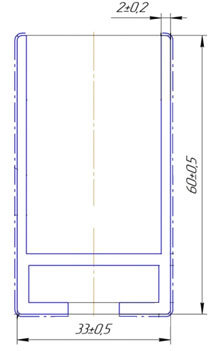
Рис. 1. Эскиз профиля
Расчет конструкции сплошной матрицы включает следующие этапы: расчет вытяжки, определение количества каналов матрицы, расчет канала матрицы и его рациональное расположение на зеркале матрицы, расчет исполнительных размеров матрицы, прочностной расчет инструмента и расчет высоты рабочих поясков.
Коэффициент вытяжки определяется как отношение площади поперечного сечения контейнера к площади поперечного сечения профиля [2]:
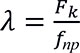 (1)
(1)
С помощью коэффициента вытяжки определяется количество каналов матрицы. В данном случае — один канал.
При расчете линейных размеров канала применяется коэффициент, учитывающий температурную усадку и растяжку профиля K = 1,012 [2].
Для расчета размеров канала матрицы используется формула:
A = Ai × K, (2)
где — номинальный линейный размер профиля; K— коэффициент усадки профиля.
Профиль располагается вертикально. Центр тяжести профиля совпадает с центром тяжести матрицы. Массивная часть профиля в нижнем положении, чтобы избежать заваливания или прогиба в процессе экструзии.
Контур форкамеры отступает от канала на 6 мм по контуру. Глубина форкамеры — 25 мм. Контур выхода канала отступает на 2 мм по контуру канала. Контур канала подкладки отступает от выхода матрицы на 4 мм (рис. 2).
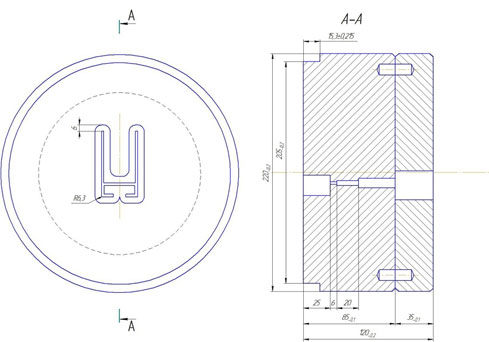
Рис. 2. Исполнительные размеры матрицы
Напряжение в сечении среза консолей матрицы не должно превышать допускаемого напряжения среза [3]:
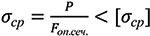 , (3)
, (3)
где P — усилие среза, F — площадь опасного сечения (рис. 3), сигма — допускаемое напряжение среза.
Усилие среза определяется по формуле [3]:
P=q*Fэл, (4)
где q — удельное давление, Fэл — площадь элемента, на которую приходится усилие прессования (рис. 3).
Удельное давление при прессовании выражается формулой [3]:
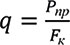 , (5)
, (5)
где P — усилие пресса, F — площадь поперечного сечения контейнера.
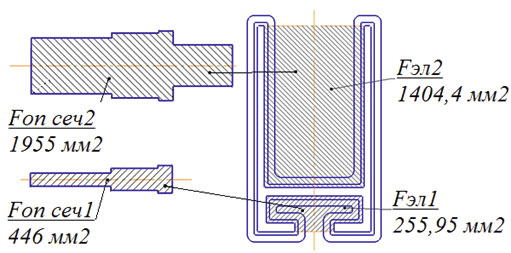
Рис. 3. Площади опасных сечений
Расчет поясков производится с помощью концентрических окружностей (графоаналитический метод), которые совмещаются с каналом матрицы. Канал матрицы разбивается на отдельные сегменты, относительно которых определяется высота поясков (рис. 4). Размер сегмента равен промеру канала матрицы и определяется из следующего соотношения [3]:
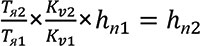 (6)
(6)
где hn1— назначаемая высота рабочего пояска, hn2 — высота рабочего пояска, полученная из расчетов, Kv1 — скоростные коэффициенты, принимаемые с помощью концентрических окружностей, Тя1, Тя2 - соотношение площадей сегментов к их периметру.
Соотношение площадей сегментов к их периметру определяется по формуле [2]:
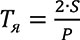 , (7)
, (7)
где S — площадь сегмента, P — периметр канала матрицы.
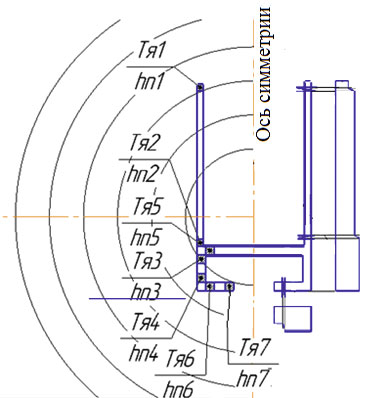
Рис. 4. Расположение канала матрицы и сегментов относительно концентрических окружностей (слева) и схема рабочих поясков
На основе расчетов смоделирована матрица в программе КОМПАС-3D. Остальной комплект инструментов (контейнер, матрицедержатель, прижимное кольцо и опорное кольцо) задан в модуле QShape программы QForm [4].
При расчете процесса прессования выявлено недопустимое смещение профиля относительно направления вектора прессования (изгиб профиля) из-за разности скоростей течения.
Скорость скорректирована за счет оптимизации геометрии матрицы: канал матрицы смещен от центра вдоль оси симметрии в сторону большей скорости течения, увеличен объем форкамеры для «подпитки» отстающей зоны, изменены длины рабочих поясков (рис. 5).
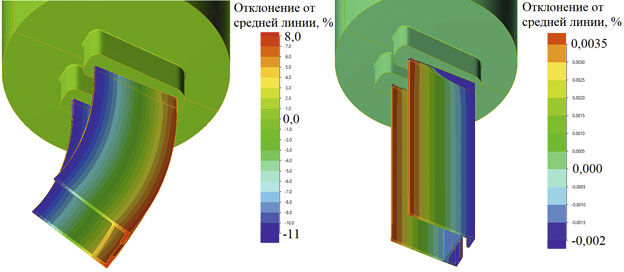
Рис. 5. Отклонения от средней линии при исходных параметрах матрицы (слева) и после оптимизации
Помимо скоростных и векторных характеристик получены аналитические данные о распределении контактного давления, остаточных напряжений, температурных полей, характере течения металла, деформации и энергосиловых характеристик.
Характер распределения остаточных напряжений получен моделированием процесса охлаждения профиля на воздухе. Анализ остаточных напряжений показал зависимость напряжений от скорости охлаждения. Края и тонкие ребра охлаждались быстрее в среднем на 5 ˚С, в них по кромке выявлены сжимающие напряжения, в то время как в середине ребер — растягивающие (рис. 6).
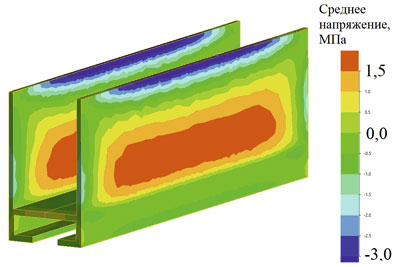
Рис. 6. Распределение остаточных напряжений в теле профиля
На примере расчета конструкции матрицы для изготовления тонкостенного профиля совместно с моделированием процесса прессования в программном комплексе QForm — Extrusion показана эффективность данной методики. Благодаря алгоритмам автоматизации процесса расчетов, получен оптимальный вариант конструкции матрицы, что снижает вероятность возникновения дефектов и недопустимых ошибок при проектировании и, как следствие, позволяет сэкономить деньги и время, затрачиваемое на подготовку производства.
Список используемой литературы:
- Гладков Ю.А., Мордвинцев П.С., Резвых Р.В., Стебунов С.А. Конечно-элементное моделирование процессов прессования алюминиевых профилей // Кузнечно-штамповочное производство. Обработка материалов давлением. 2018. № 3. С. 21-38.
- Каргин В.Р. Основы технологических процессов ОМД: раздел прессование: учеб. пособие / В.Р. Каргин, Б.В. Каргин. Самара: Изд-во СГАУ, 2011. 104 с.: ил.
- Каргин В.Р., Каргин Б.В., Арышенский Е.В. Технология прессования профилей из легких сплавов: метод. указания / сост.: Самара: Изд-во СГАУ, 2012. 54 с.
- Гладков Ю.А., Каневский С.С. Моделирование прессования алюминиевых профилей в новой версии программы QForm Extrusion VX: совместная деформационная задача // Кузнечно-штамповочное производство. Обработка материалов давлением. 2016. № 11. С. 41-48.


