Опыты с моделированием игральных костей неожиданно привели к выявлению новой(?) группы геометрических тел, объединенных мной в категорию «Шароусеченные аналоги платоновых и каталановых тел». Вообще, придумать чтолибо новое достаточно трудно, поскольку мыслящих людей на Земле — семь с лишним миллиардов ☺.
По каким признакам (параметрам) они являются аналогами? Каждое из этих тел имеет равное количество граней с одним из платоновых или каталановых тел. Число сопряжений касания каждой грани с соседними гранями совпадает с числом сопряжений грани соответствующего многогранника. Двугранные углы соответствующих пар равны между собой. Главное отличие — форма граней. У описываемых шароусеченных тел грани круглые одного размера.
На рис. 15 показаны модели шароусеченных аналогов тел Платона.

Рис. 1. Аналог тетраэдра: 4 грани; 4 сферических участка. Двугранный угол 70,53°

Рис. 2. Аналог гексаэдра: 6 граней; 8 сферических участков. Двугранный угол 90°

Рис. 3. Аналог октаэдра: 8 граней; 6 сферических участков. Двугранный угол 109,47°

Рис. 4. Аналог додекаэдра: 12 граней; 20 сферических участков. Двугранный угол 116,57°

Рис. 5. Аналог икосаэдра: 20 граней; 12 сферических участков. Двугранный угол 138,19°
Примечание: десятичные значения углов округлены.
На рис. 618 показаны модели шароусеченных аналогов каталановых тел.

Рис. 6. Аналог ромбододекаэдра: 12 граней; 14 сферических участков. Двугранный угол 120°
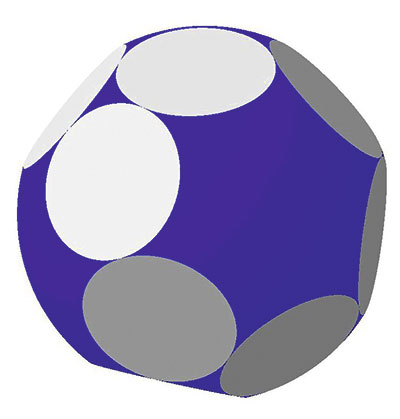
Рис. 7. Аналог триакистетраэдра: 12 граней, параллельных нет; 8 сферических участков. Двугранный угол 129,52°
Примечание: десятичные значения углов округлены.
Обратите внимание на сферические участки тел. У аналогов платоновых тел эти участки одинаковы для каждого отдельно взятого тела. У каждого из аналогов каталановых тел эти участки двух или трех типов (3, 4, 5, 6, 8 и 10лучевые звезды). Сочетание круглых граней и звездчатых участков создает своего рода мозаику, равномерно расположенную на поверхности шара и при этом индивидуальную для каждого из шароусеченных тел.
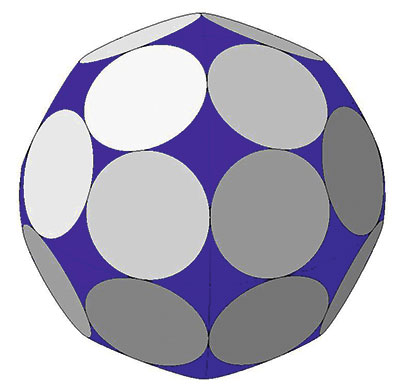
Рис. 8. Аналог дельтоидального икоситетраэдра: 24 грани; 26 сферических участков. Двугранный угол 138,12°
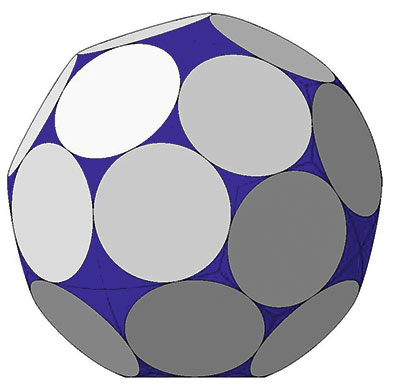
Рис. 9. Аналог пентагонального икоситетраэдра: 24 грани, параллельных нет; 38 сферических участков. Двугранный угол 136,3°

Рис. 10. Аналог тетракисгексаэдра: 24 грани; 14 сферических участков. Двугранный угол 143,13°
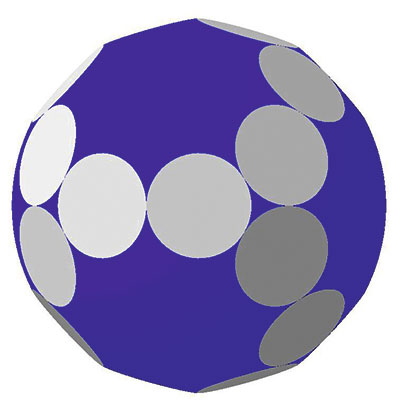
Рис. 11. Аналог триакисоктаэдра: 24 грани; 14 сферических участков. Двугранный угол 147,35°

Рис. 12. Аналог ромботриаконтаэдра: 30 граней; 32 сферических участка. Двугранный угол 144°

Рис. 13. Аналог гекзакисоктаэдра: 48 граней; 26 сферических участков. Двугранный угол 155,08°
Что касается применения, то полученные разнообразные мозаики усеченных шаров можно использовать как варианты огранки ювелирных изделий. В предыдущих статьях я уже предлагал использовать шароусеченные тела в качестве игральных костей, елочных игрушек и сувениров.

Рис.14. Аналог дельтоидального гексеконтаэдра: 60 граней; 62 сферических участка. Двугранный угол 154,12°

Рис. 15. Аналог пентагонального гексеконтаэдра: 60 граней, параллельных нет; 92 сферических участка. Двугранный угол 153,18°

Рис. 16. Аналог пентакисдодекаэдра: 60 граней; 32 сферических участка. Двугранный угол 156,72°

Рис. 17. Аналог триакисикосаэдра: 60 граней; 32 сферических участка. Двугранный угол 160,61°

Рис. 18. Аналог гекзакисикосаэдра: 120 граней; 62 сферических участка. Двугранный угол 164.89°
Не исключаю, что ктото из читателей захочет построить модели шароусеченных аналогов. Для них совет: начинать надо с построения многоугольников исходных многогранников (это касается каталановых тел). Сами многогранники строить необязательно. Тем, кто пока не освоил 3D, можно посоветовать потренироваться на вкусных и полезных астраханских арбузах перед тем, как их съесть, — двойная польза будет ☺.
Да здравствуют Шароусеченные и КОМПАС, в котором они построены!


