На смену традиционным зуборезным технологиям изготовления зубчатых колес приходят новые цифровые технологии на основе ЧПУ, которые уже сейчас превосходят первые по универсальности, унификации и простоте инженерных расчетов.
Мир меняется. Меняются методы проектирования, технологии, оборудование. Специалисты тоже меняются. И первый «звоночек», сообщающий о грядущих проблемах в изготовлении зубчатой пары шестерен конического косозубого зацепления с эписиноидной формой зуба, состоялся в недалеком прошлом, около 10 лет назад, и представлял собой описание нестандартного проекта, выполненного в САМ-системе ГеММа-3D (Форум cccp3d.ru, Конкурс-2010, номинация «Технология»). Сам факт того, что на упомянутый проект обратили внимание технологи ЧПУ, говорит о том, что в настоящее время в производстве шестерен имеются серьезные проблемы. Для начала предлагаем ознакомиться с историей вопроса и оригиналом сообщения, в котором описывалось решение поставленной задачи.
Заказчик обратился с проектом, который ему не удавалось реализовать в течение девяти месяцев. Четыре специалиста брались за эту работу, но во всех случаях результат оказался отрицательным. Это был вызов для профессионального самолюбия специалиста! На фоне того, что уже почти все ЧПУработы при достижении определенного опыта становятся скучными, это было чтото новенькое — головоломка с неизвестным окончанием. Заказчику требовалось изготовить пару зубчатых колес конической косозубой передачи с редкой формой зуба. Всех отпугивало странное и непонятное слово «эписиноида». Решено было попробовать. Параметры одной из деталей — шестерни — приведены на рис. 1.
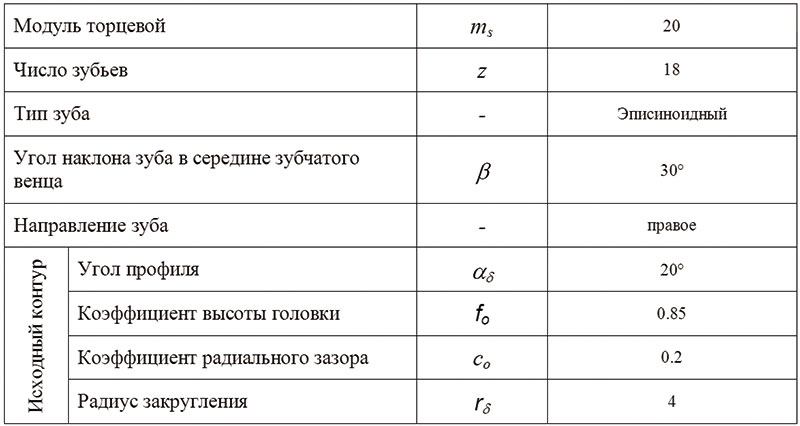
Рис. 1. Таблица параметров шестерни
Работа началась с поиска этого странного слова — «эписиноида». В современных справочниках по математике, физике, технологии и конструированию ничего не нашлось. Удалось обнаружить лишь в Большой советской энциклопедии 1928 года. Оказалось, что это довольно известная кривая, только названия ее никто не знает.
Для справки. Если рассечь зуб шестерни поперек, то мы увидим тело зуба, ограниченное двумя эвольвентами. А если смотреть вдоль зуба, то можно различить несколько вариантов формы зуба. Цилиндрические колеса могут быть прямозубые, косозубые и шевронные. Конические шестерни тоже бывают прямозубыми, и там все абсолютно ясно. А конические косозубые шестерни бывают с тангенциальной и круговой формой зуба. И только такие делают в России, потому что их достаточно просто изготавливать на специальном оборудовании без ЧПУ. Но в поставленной задаче нужно было изготовить эписиноидную форму зуба.
Эписиноида — это плоская кривая, такая, что для каждой точки кривой угол между отрезком, соединяющим центр эписиноиды с текущей точкой, и касательной, проведенной из этой точки к эписиноиде, всегда является постоянным. То есть если из любой точки кривой построить касательную и радиус к центру кривой, то везде угол между касательной и радиусом будет иметь одно и то же значение. Это свойство обеспечивает наивысшую плавность хода зубчатой передачи и равномерность передачи крутящего момента. Но самое главное — постоянство направлений силового взаимодействия внутри зубчатого зацепления в разных точках контакта. Поэтому эписиноидная форма зуба применяется для тяжело нагруженных зубчатых передач.
Есть еще одно свойство этой замечательной кривой, граничащее с фантастической невозможностью представления. Сравним три кривых: спираль Архимеда, эвольвенту и эписиноиду. Спираль Архимеда начинается в нуле и разворачивается наружу до бесконечности. Эвольвента начинается с базовой окружности и разворачивается наружу до бесконечности. Эписиноида, как и две предыдущие кривые, разворачивается наружу до бесконечности. Но самое удивительное — при движении в точку нуля она тоже стремится к бесконечности. Движется к точке нуля, но никогда ее не достигает…
Вполне естественно, что в стандартном наборе инструментов, предлагаемых САМсистемой ГеММа3D, этой кривой не нашлось. Пришлось строить с помощью вспомогательных инструментов: макроса и кривой по формуле. Контроль результата показал, что кривая, созданная макросом, выполнена с меньшими отклонениями от идеального угла в 30 градусов. Поэтому она была выбрана для дальнейших построений.
Следующим действием нужно развернуть плоскую эписиноиду на два делительных конуса зубчатой пары. Инструмент для развертки в САМсистеме ГеММа3D был, но для точного позиционирования кривой на конусе и для абсолютной уверенности в правильности результата тоже пришлось подготовить макрос. Размещаем плоскость построенной эписиноиды в зоне контакта делительных конусов зубчатого венца и шестерни касательно к ним. Макрос создал две кривые на делительных конусах шестерен. Каждую из полученных кривых тоже можно назвать эписиноидой, потому что они имеют те же самые свойства (рис. 2).
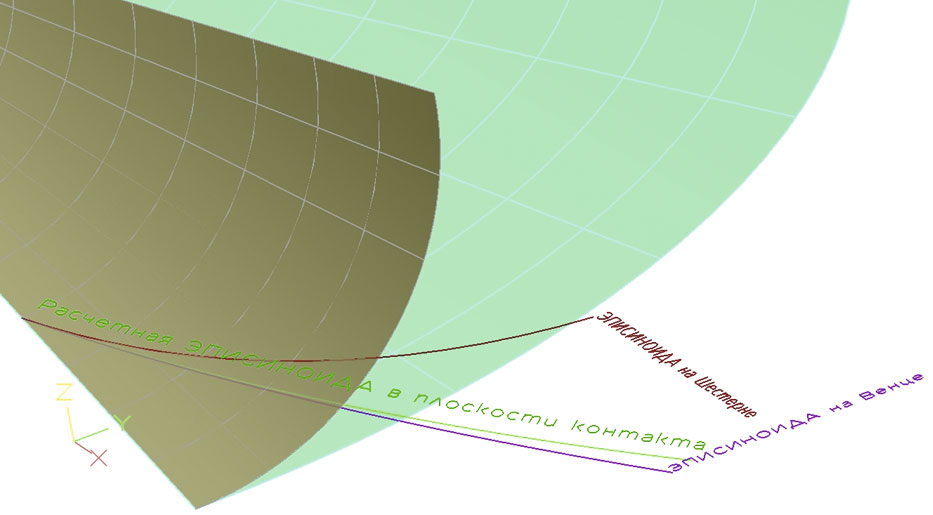
Рис. 2. Наворачивание эписиноиды на конусы
Далее уже можно было переходить к построению профиля зуба, но здесь тоже оказался подводный камень. Дело в том, что эвольвента для конических колес строится не на плоскости, а на сфере. И все расчетные формулы, которые для цилиндрических колес были линейными, для конических колес не подходят. Плоскость бесконечна, а сфера ограниченна, поэтому все формулы стали нелинейными, а все расчеты — более хитрыми. И опять в инструментарии САМсистемы не оказалось эвольвенты для сферы. Пришлось создавать еще один макрос, который помог решить эту задачку (рис. 3).
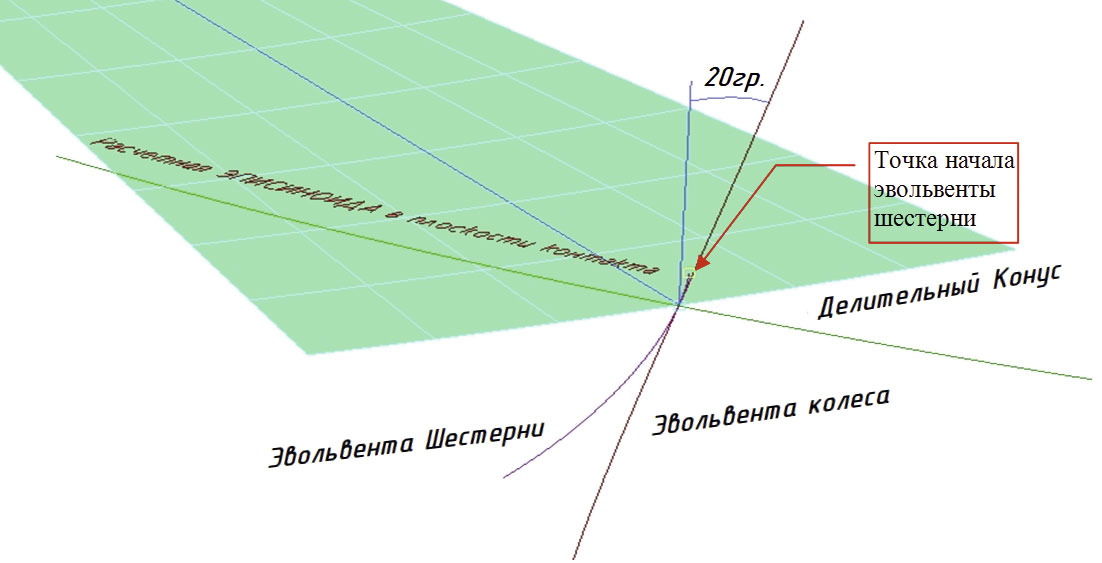
Рис. 3. Эвольвенты на контактном конусе
Используя созданные кривые, уже можно переходить к построению рабочих поверхностей зубьев. Для этого расставляем «сферическую» эвольвенту по эписиноиде. При этом каждую кривую необходимо поставить под определенным углом и масштабировать пропорционально расстоянию до центра пересечения осей зубчатых колес. При наличии подходящего инструмента САМсистемы это достаточно просто. Строим боковые поверхности зубьев по набору сечений, затем — поверхности вершин и впадин. Получаем расчетные поверхности венца и шестерни (рис. 4).

Рис. 4. Расчетные поверхности
На этом этапе уже можно проверить результат работы на точность. Выбираем несколько зубьев венца и шестерни и режем их произвольной плоскостью. Проверяем сечения зубчатых колес на взаимное пересечение и получаем результаты, показанные на рис. 5. На самом деле такие красивые цифры получились не с первого раза. Вначале наблюдалось пересечение контуров. Чтобы избавиться от него, пришлось уменьшить толщину зубьев венца смещением всех правых рабочих поверхностей венца на 0,4 мм.
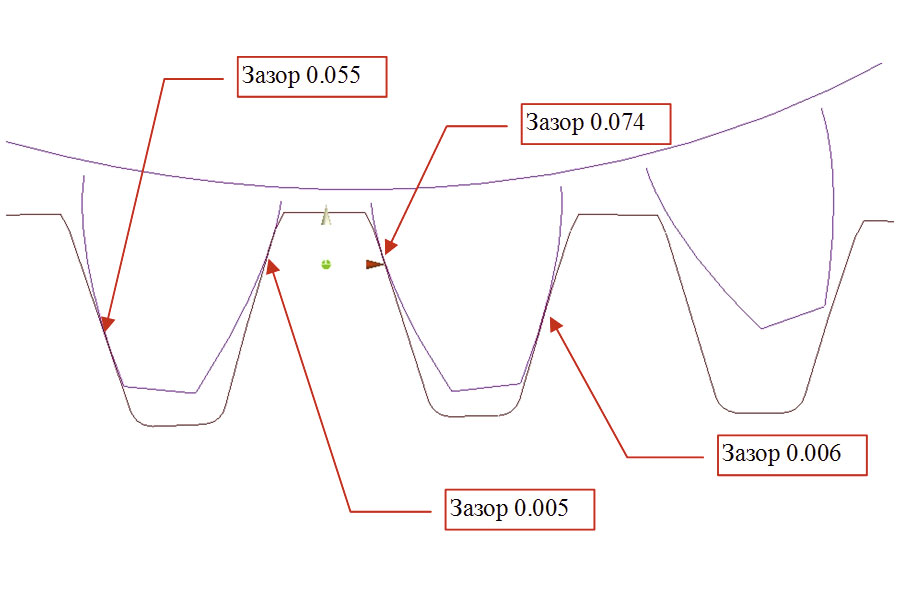
Рис. 5. Результаты обмера модели
Для закрепления успеха выполняем обмер зуба так, как это будет делать работник ОТК. Для столь непрямоугольных поверхностей это достаточно непросто. На определенном расстоянии от внешнего торца зубьев выбирается перпендикулярное сечение зуба, в этом сечении на определенной глубине от вершины зуба должен получиться определенный размер. На рис. 6 показан фрагмент чертежа и эскиз с размерами, снятыми с математической модели. На эскизе указаны два числа, определяющих контрольный размер, — до и после (в скобках) уменьшения толщины зубьев венца.
Удостоверившись в правильности достигнутого решения, строим остальные поверхности зубчатых колес — поверхностей перехода у дна и фаски на выступе. Затем строим целиком поверхности зубчатых колес для завершенности изделия (рис. 6).
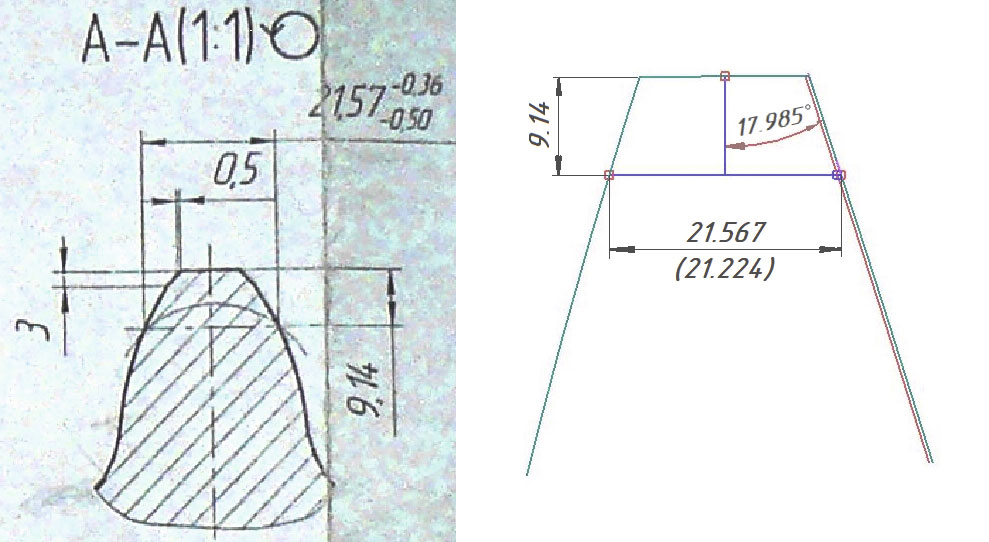
Рис. 6. Сечение А-А колеса
После утверждения модели (рис. 7) заказчиком работа превратилась в обычное программирование ЧПУ. Изготовление венца было выполнено обычной фрезерной 3Dобработкой. Но в обработку шестерни пришлось вложить чуть больше сил. Зубья шестерни тоже можно было выполнить обычной позиционной фрезерной 3Dобработкой. Но тогда изза поднутрения пришлось бы выполнять обработку каждой стороны зуба за два раза. Для улучшения качества поверхности было решено применить фрезерную 4Dобработку (рис. 8 и 9).

Рис. 7. Модель зубчатой пары в сборе

Рис. 8. Шестерня во время 4D-обработки

Рис. 9. Венец и модель шестерни в контакте
Пробная обработка была выполнена на деревянных моделях, значительно подпорченных неудачливыми предшественниками. Затем был обработан металл.
В настоящее время изготовленная зубчатая пара трудится гдето на севере на одной из буровых установок.
Поскольку в сообщении был описан весьма нестандартный способ обработки зубчатых колес, некоторые участники форума приняли его в штыки. Развернулась серьезная дискуссия, посвященная сравнению двух подходов к проектированию и изготовлению зубчатых колес.
Традиционный способ проектирования и изготовления зубчатых колес получил название «Вариант Б». Он предполагает изготовление зубчатых колес методом обкатывания специальным профильным режущим инструментом: зубчатая рейка, долбяк, резцовая круговая головка, профильные резцы и др. Описанный в сообщении форума подход получил название «Вариант А». От Варианта Б он отличается тем, что не использует обработку специальным режущим инструментом, вследствие чего значительно упрощается проектирование и производство зубчатых колес. Поскольку проектирование и изготовление для сложных форм зубьев можно выполнить только с помощью компьютерной техники, будем считать Вариант А цифровым методом.
Первый обсуждаемый вопрос — чем обусловлено применение именно такого зубчатого зацепления? Действительно, почему нельзя было подобрать передаточное и сделать пару конических, ведь требовалась именно пара? Этим вопросом также был озадачен автор конкурсной работы. И ответов было несколько.
Политический ответ — это жесткие пожелания заказчика. Только эписиноидная форма зуба! Другая не принимается. Технический ответ, полученный из различных источников — эписиноида обеспечивает максимальную плавность работы передачи и суммарный вектор силы не изменяет своего направления в контакте с разными точками профиля зубьев.
Серьезно обсуждалось понятие «пара зубчатых колес». Косозубые конические колеса изготавливают с различной формой зуба: тангенциальная, круговая, эписиноидная. Если колесо изготовлено с круговым зубом, то и шестерня должна быть изготовлена с круговым зубом, другая форма зуба не подходит. И это естественно. Одним из пожеланий автора сообщения было изготовленную по его расчетам шестерню примерить с реальным эписиноидным колесом, но заказчик отказался. А участники форума, имеющие опыт реальной работы на зуборезных станках, объяснили причину отказа. Дело в том, что, вопервых, для обработки каждой формы зуба существуют специальные станки для обработки только одной формы зуба. Вовторых, параметры формы зуба зависят от конкретной наладки станка. Шестерню и колесо необходимо изготавливать с одной наладки механизмов, обеспечивающих нужную форму зуба. Шестерни, изготовленные на разных станках разными наладчиками с помощью разных наладок, сопрягаться не будут. Поэтому изготавливают с одной наладки сразу пару колес либо нужное количество колес этой пары. Именно за счет изготовления пары обеспечивается нормальная работоспособность косозубых конических колес.
Опытные зуборезчики сомневались в правильности построения модели по Варианту А. Для них непонятен чисто математический способ задания эвольвентной линии обкатывания. Обкатывание инструментом визуально наглядно и понятно, оно по определению является обкатыванием. А как выполняется обкатывание прямым построением поверхности по формулам? Да еще эвольвентой, построенной на сфере! Любые математические, геометрические и логические «доводы» в защиту Варианта А оказались бесполезными. Если бы у идеи цифрового моделирования зубчатых колес не было серьезного подтверждения правильности расчетов, вполне возможно, что на этом дискуссия окончилась бы без реализации в производстве. Но как раз реализация этих расчетов в металле с проверкой работоспособности и послужила неоспоримым фактом возможности цифрового проектирования зубчатых колес без имитации обкатывания. Прямое построение рабочих поверхностей зубьев подтверждено опытом.
И когда уже модель была построена, ни у кого не осталось сомнений в возможности ее изготовления на станках с ЧПУ. Обсуждение перешло в экономическую область — какой из вариантов дешевле? Особых разногласий не было. Получилось, что для массового и крупносерийного производства более выгодным является Вариант Б. Однако для изготовления мелких партий и единичного производства Вариант А более экономичен. Причем для изготовления уникальных и крупногабаритных зубчатых колес Вариант А оказывается единственно возможным.
В последних комментариях участники форума доказали автору сообщения, что в предложенном проекте была использована не эписиноида. Оказалось, что автор, изучая свойства эписиноиды по материалам Большой советской энциклопедии 1928 года, ошибся. Пытаясь повторить кривую по описанию ее характеристик, он по факту получил логарифмическую спираль. И не случайно. Во времена, когда не было компьютеров и числового программного управления (ЧПУ) станками, изготовители зубчатых колес знали о существовании логарифмической спирали и ее полезных свойствах, важных для механических передач. Но, к сожалению, им не удалось создать механизм, способный воспроизвести требуемую кривую. Поэтому они использовали кривую, имеющую минимальные отклонения от логарифмической спирали.
Такой кривой и оказалась эписиноида (от греч.: эпи — над, синоид — сокр. от синусоиды). Это часть синусоиды, возможно, с небольшой модификацией на уровне эквидистанты. Автор сообщения «по ошибке» выполнил логарифмическую форму зуба — ту самую, к которой стремились инженеры начала прошлого века. Это наилучшая форма зуба для косозубых конических колес. А в инженерном проектировании логарифмическая спираль дает возможность легко проектировать зубчатые колеса. Простота и однозначность создания рабочих поверхностей позволяют унифицировать зубчатые колеса настолько, что колеса одной пары могут быть рассчитаны разными конструкторами, изготовлены на разных станках, разными наладчиками и при этом будет обеспечена работоспособность пары.
Подводя итоги, следует констатировать, что промышленные технологии претерпевают серьезные изменения. Подтверждением является тот факт, что описанный проект оказался у ЧПУшников. Традиционные технологии становятся морально устаревшими — речь не идет о спаде, но стагнация уже наступила. Зуборезное оборудование не развивается, специалистов становится всё меньше. Зато цифровые технологии, способные изготовить практически что угодно, сейчас на подъеме.
Традиционные технологии имеют опыт применения, измеряемый десятилетиями, и поддерживаются многочисленными методиками и ГОСТами. Поэтому еще долгое время они будут основными в машиностроении. А чтобы цифровые технологии получили массовое распространение, необходимо провести серьезную работу по созданию новых расчетных методик и их документальной поддержке.



