Инженерные расчеты зубчатых колес с помощью T-FLEX Анализ интегрированной с T-FLEX CAD среды конечно-элементных расчетов

Александр Иващенко
К.т.н., доцент кафедры «Естественно-научные дисциплины» КТИ (­филиала) ВолгГТУ.

В статье рассмотрен метод оценки статичес­кой прочности по относительным эквивалентным напряжениям зубчатых колес и передачи в целом с помощью T-FLEX Анализ интегрированной с T-FLEX CAD среды конечно-элементных расчетов, которая включена в Единый реестр российских программ.

На этапе проектирования изделия разрабатываемая конструкция должна отвечать определенным критериям работоспособности. Работоспособность — это состояние, при котором изделие способно выполнять заданные функции с параметрами, установленными нормативно­технической документацией. Одним из ключевых параметров является прочность. При нарушении прочности в изделиях возникают недопустимо большие остаточные деформации, поверхностные разрушения или преждевременные поломки. На сегодняшний момент актуальна задача прогнозирования поведения конструкции при заданных нагружениях, предупреждения и дальнейшего исключения мест, имеющих недостаточный либо излишний запас прочности, а также стремление разработать равнопрочную конструкцию. Данная задача решается на этапе инженерного расчета, который может выполняться аналитическими или численными методами. Зачастую в сложных расчетах эти методы тесно переплетаются друг с другом. Например, первый этап — аналитическая оценка действующей нагрузки и мест ее приложения, второй этап — использование численных методов для оценки прочности и других параметров изделия, третий этап — анализ полученных результатов. Лидирующим методом численного решения является метод конечных элементов (МКЭ) — универсальное решение, охватывающее широкий круг прикладных задач с хорошей численной устойчивостью МКЭ­алгоритмов.

Работа конструктора — процесс творческий: с одной стороны, проектируемое изделие должно отвечать критериям работоспособности, с другой — иметь невысокую себестоимость и минимальные издержки в производстве. Поиск такого баланса можно сопоставить с работой ювелира по огранке драгоценного камня, поэтому на помощь конструктору в решении современных сложных задач приходят CAD/CAE­системы, позволяющие снизить трудозатраты, повысить эффективность, а в некоторых случаях — полностью упростить однотипные, рутинные операции. Причем в таких системах можно совместить этапы разработки конструкторской документации и инженерных расчетов без привлечения сторонних помощников или организаций.

Большинство изделий включают в себя передаточные механизмы, которые могут состоять из зубчатых передач и других элементов. Одна из задач проектирования зубчатой передачи — поиск рациональной конструкции колес. Решить такую задачу конструктору будет затруднительно используя только CAD­системы. При разработке конструкции колеса или более сложного изделия — вала­шестерни необходимо руководствоваться различными нормативными документами по расчету геометрии, оценке статической прочности, усталостной выносливости и прочих требований. Совместное применение CAD/CAE­систем позволяет конструктору на этапе проектирования дополнительно проводить оценку работоспособности колес по критерию прочности, так как прочность зуба и колеса в целом влияет на надежность и долговечность узла механизма, что, в свою очередь, снижает время на поиск рационального решения.

Одной из таких CAD/CAE­систем, представленных на российском рынке, является программное обеспечение от компании «Топ Системы». Используя T­FLEX CAD при конструировании зубчатых передач конструктору предоставляется широкий набор средств проектирования, расчета и анализа их геометрии, оформления конструкторской документации в соответствии с ЕСКД. Применяя интегрированную среду в T­FLEX CAD — T­FLEX Анализ (статический анализ), у конструктора на этапе проектного расчета появляется возможность произвести оценку статической прочности по относительным эквивалентным напряжениям с целью минимизаций ошибок проектирования или поиска конструкции, обладающей минимальной массой при достаточной прочности.

В статье приведен способ оценки статической прочности зубчатой передачи и ее элементов (колесо и вал­шестерня)с помощью T­FLEX Анализ. В основу способа положен метод [1], в котором контакт сопряженных зубьев рассматривается как сжатие двух цилиндров (рис. 1) под действием удельной нормальной силы с радиусами кривизны сопряженных поверхностей ρ1 и ρ2 по площадке в среднем шириной 2а.

Рис. 1. Модель контактирующей пары зубьев по методу [1]

Например, такой метод использовался в статье [2], где авторами произведена оценка напряжений по критерию Мизеса прямозубой шестерни из стали 20ХН3А тягового редуктора локомотива в программах инженерного анализа по выделенной площадке контакта на боковой поверхности зуба в момент трогания локомотива. В статье [3] также с помощью пакета программ инженерного анализа проведен анализ прочности по критерию Мизеса для косозубой шестерни планетарного редуктора в квазистатических условиях. В работах [4, 5, 6] авторы приводят еще один возможный способ оценки прочности зубчатых передач и ее элементов при помощи CAE­систем.

Рассчитываемая цилиндрическая прямозубая зубчатая передача состоит из двух элементов: вал­шестерня (рис. 2а) и колесо (рис. 2б). Параметры передачи: модуль m = 4 мм; число зубьев шестерни z1 = 19 шт., колеса z2 = 81 шт.; ширина шестерни bw1 = 72 мм; ширина колеса bw2 = 67 мм; межосевое расстояние aw =  200 мм; окружное усилие в зацеплении Ft = 4018,5 Н.

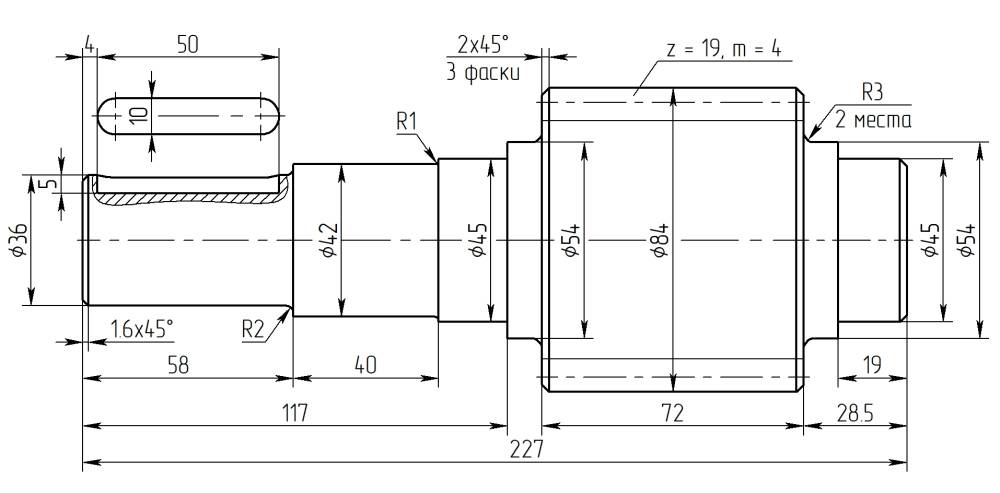
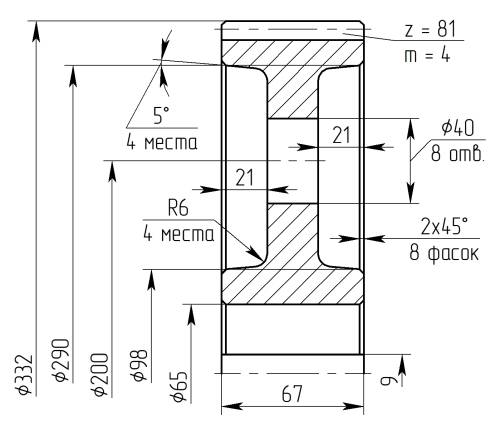
Рис. 2. Эскизы вала-шестерни и колеса цилиндрической прямозубой зубчатой передачи

Материал колес — сталь конструкционная легированная марки 40ХН, твердость 200­240 HB, предел текучести σТ = 570 МПа, предел прочности σВ = 780 МПа, модуль упругости первого рода E = 2 × 10⁵ МПа, коэффициент Пуассона µ = 0,3.

Рассматривается контакт сопряженных зубьев для однопарного зацепления в данный момент времени (рис. 3).

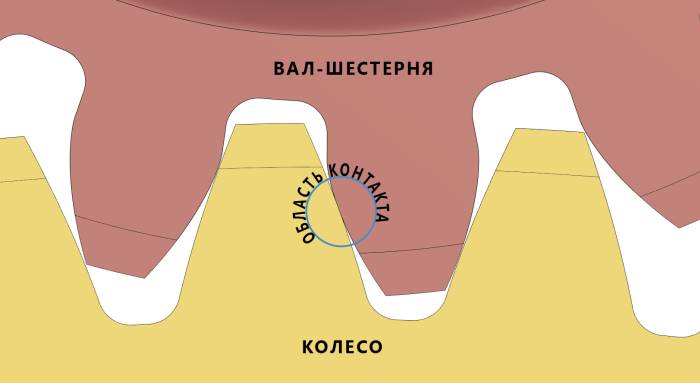
Рис. 3. Сопряженная пара зубьев

По информации в литературе [1, 7], получены формулы (1­3), используемые в расчетах прямозубого внешнего эвольвентного цилиндрического зацепления. Для расчета косозубого внешнего эвольвентного цилиндрического зацепления необходимо использовать формулы, приведенные в [8, 9].

Полное нормальное усилие:

Fn = Ft  × K/cosαtw = 6113,84 Н,               (1)

где K = K_А × K_Hα × K_Hβ × K_HV — коэффициент расчетной нагрузки, К = 1,42967 и α_tw по [7].

Удельная нормальная сила для прямозубого зацепления с одной контактирующей парой зубьев:

ω = Fn /bw2 = 91,251 Н/мм.                      (2)

Полуширина плоскости контакта:

     (3)

T­FLEX Анализ позволяет решать задачи на основе одного или нескольких твердых тел. В статье исследуются задачи статической прочности по отдельному нагружению вала­шестерни и колеса, а также контактная задача, в которой рассматривается контакт зубьев передачи с двумя телами (рис. 3). При решении первой группы задач по нагружению одного тела проделаны дополнительные операции как у шестерни, так и у колеса: с помощью вспомогательных поверхностей и команды «Разделение граней»в зоне начальной поверхности была выделена на боковой грани контактирующего зуба область шириной 2а и длиной, равной ширине венца колеса. Это позволило приложить действующую нагрузку Fn нормально к выделенной поверхности в полюсе зацепления. При решении контактной задачи аналогичным образом на боковой поверхности контактирующего зуба колеса получена линия, проходящая через полюс зацепления. С помощью команды «Сопряжение» было организовано касание боковой поверхности контактирующего зуба шестерни и выделенной линии на зубе колеса. Кроме того, были заданы другие сопряжения, ограничивающие перемещение тел относительно друг друга таким образом, чтобы колеса имели возможность вращения вокруг своих осей без нарушения зацепления в зоне выделенного контакта зубьев, что позволило организовать однопарный контакт зубьев колеса и шестерни. Нагрузка была приложена к выходному концу вала­шестерни по цилиндрической поверхности диаметром 36 мм (см. рис. 2а) в виде вращающего момента с учетом коэффициента расчетной нагрузки.

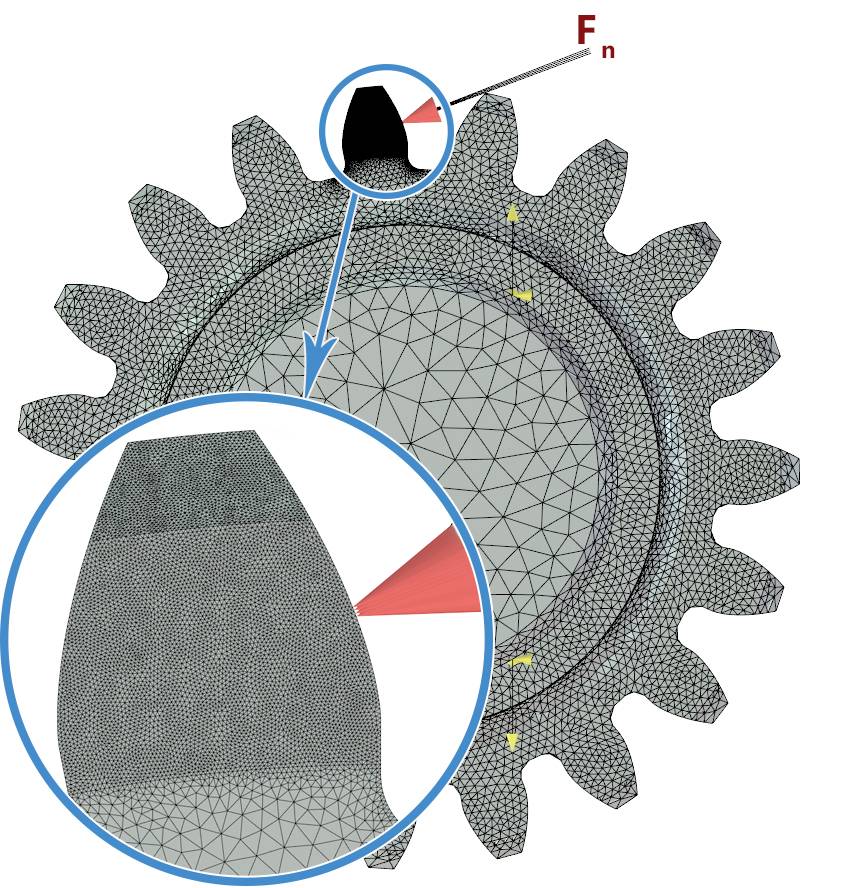
На следующем этапе произведено построение тетраэдральной конечно­элементной сетки с помощью линейных четырехузловых элементов. В местах, где предполагаются большие градиенты напряжений, а также в местах плавных переходов поверхностей сетка более мелкая. На рис. 4 и 5 приведено изображение сетки на исследуемых элементах и передачи в целом. Число объемных конечных элементов: вал­шестерня — 2,66 млн (рис. 4а); колесо — 7,3 млн (рис. 4б); контактная задача — 1,05 млн (рис. 5).

a

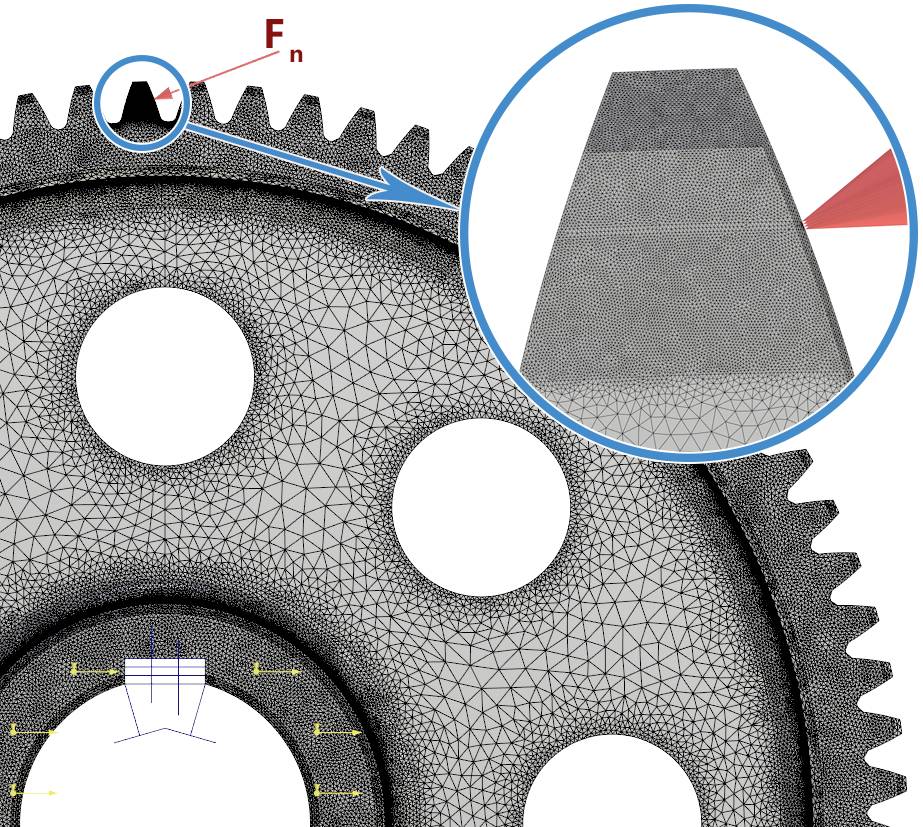b

Рис. 4. Сеточная конечно-элементная модель вала-шестерни и колеса

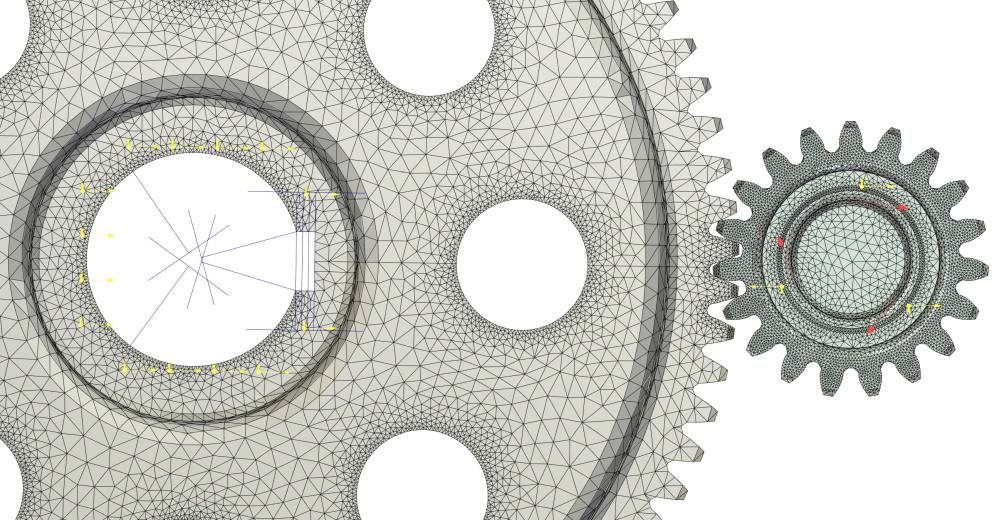
Рис. 5. Сеточная конечно-элементная модель зубчатой передачи

Для поверхностей использованы ограничения по перемещениям двух типов: полное закрепление и частичное закрепление в цилиндрической системе координат с ограничением движения в радиальном направлении и по оси вращения. При решении первой группы задач: для вала­шестерни (см. рис. 2а и 6) применено полное закрепление — поверхность диаметром 36 мм, включая боковые грани шпоночного паза, частичное — две поверхности диаметром 45 мм (цапфы вала); для колеса (см. рис. 2б и 7) применено полное закрепление — посадочная поверхность диаметром 65 мм, включая боковые грани шпоночного паза, частичное — две торцевые поверхности ступицы колеса. Для контактной задачи (рис. 8): полное закрепление — посадочная поверхность колеса, с учетом боковых граней шпоночного паза; частичное — торцевые поверхности ступицы колеса и цапфы вала.

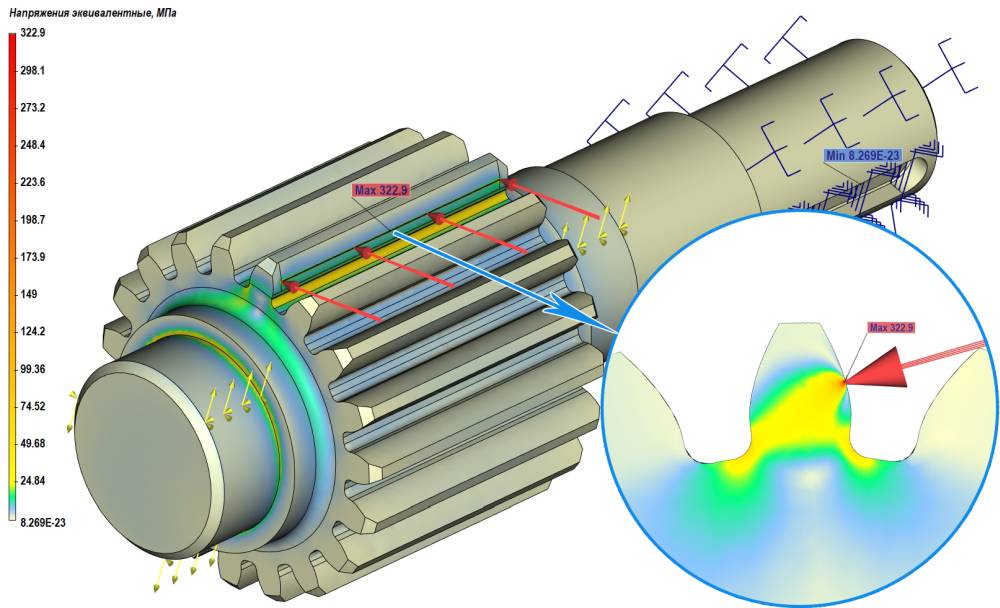
Рис. 6. Распределение относительных эквивалентных напряжений в вале-шестерне

В T­FLEX Анализ произведен конечно­элементный расчет статической прочности вала­шестерни, колеса и передачи в целом на основе их объемных конструкций, где твердотельные модели построены в T­FLEX CAD. Определены относительные эквивалентные напряжения σэкв, которые вычислялись из компонентов тензора напряжений согласно IV теории прочности [10]. Получена картина распределения напряжений: вал­шестерня (см. рис. 6)  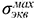— = 322,9 МПа, колесо зубчатое (см. рис. 7) — 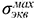= 318,1 МПа, передача зубчатая (см. рис. 8) — 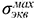= 322,6 МПа.

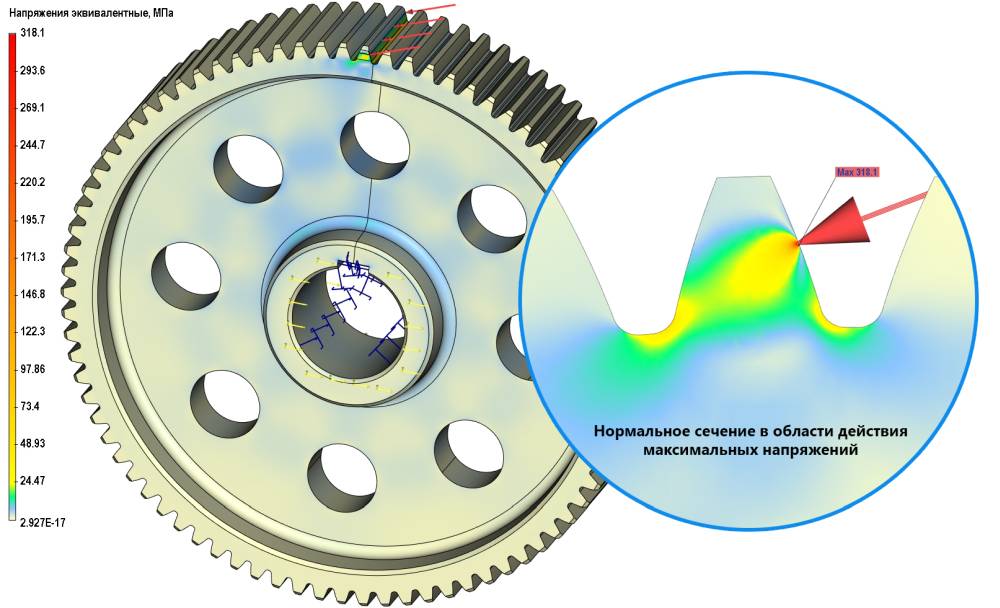
Рис. 7. Распределение относительных эквивалентных напряжений в колесе зубчатом

Зуб шестерни (см. рис. 6) имеет более высокую интенсивность значений напряжений, чем зуб колеса (см. рис. 7) при одинаковой нагрузке Fn. Рассматривая картину распределения напряжений в контактной задаче (рис. 8) — такой эффект тоже можно наблюдать.  Контактные задачи удобнее применять если необходимо рассмотреть работу передачи в целом, но ресурсные затраты вычислительной техники увеличиваются. Решение задачи по нагружению только одного элемента (шестерни или колеса) оказывается эффективным в плане экономии времени, причем порядок значений напряжений сопоставим с результатами решения контактной задачи двух тел. С точки зрения наложения граничных условий контактная задача будет рациональной. С учетом некоторых идеализированных условий решения задачи, при которых не рассматривались погрешности изготовления и неточности монтажа, возможные деформации вала с перекосом осей в процессе работы передачи, использовался однородный и изотропный материал, допустимо применение нагружения только одного элемента из двух в передаче.

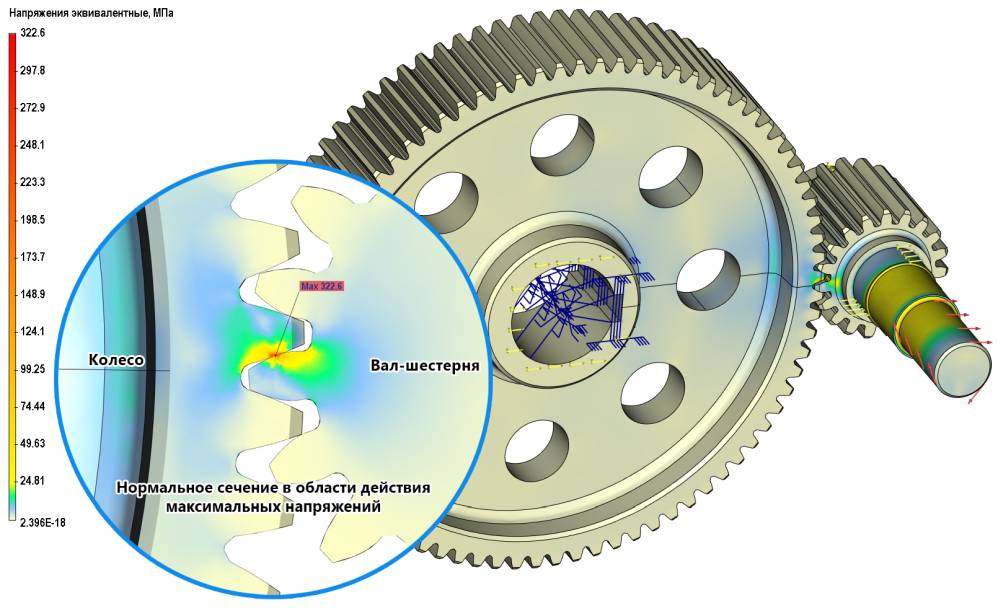
Рис. 8. Распределение относительных эквивалентных напряжений в передаче зубчатой

Определен запас статической прочности по эквивалентным напряжениям относительно допускаемых напряжений, то есть напряжений предела текучести для выбранного материала. Получено, что для вала­шестерни запас составил 1,765 (рис. 9), для колеса — 1,792 (рис. 10). Минимально допустимый запас — 1,1.

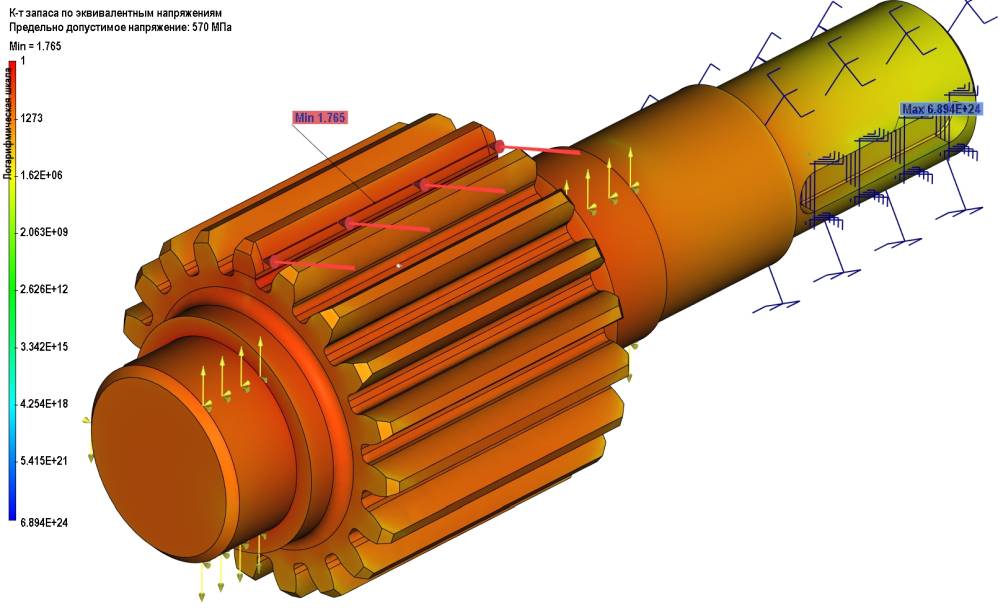
Рис. 9. Запас статической прочности вала-шестерни

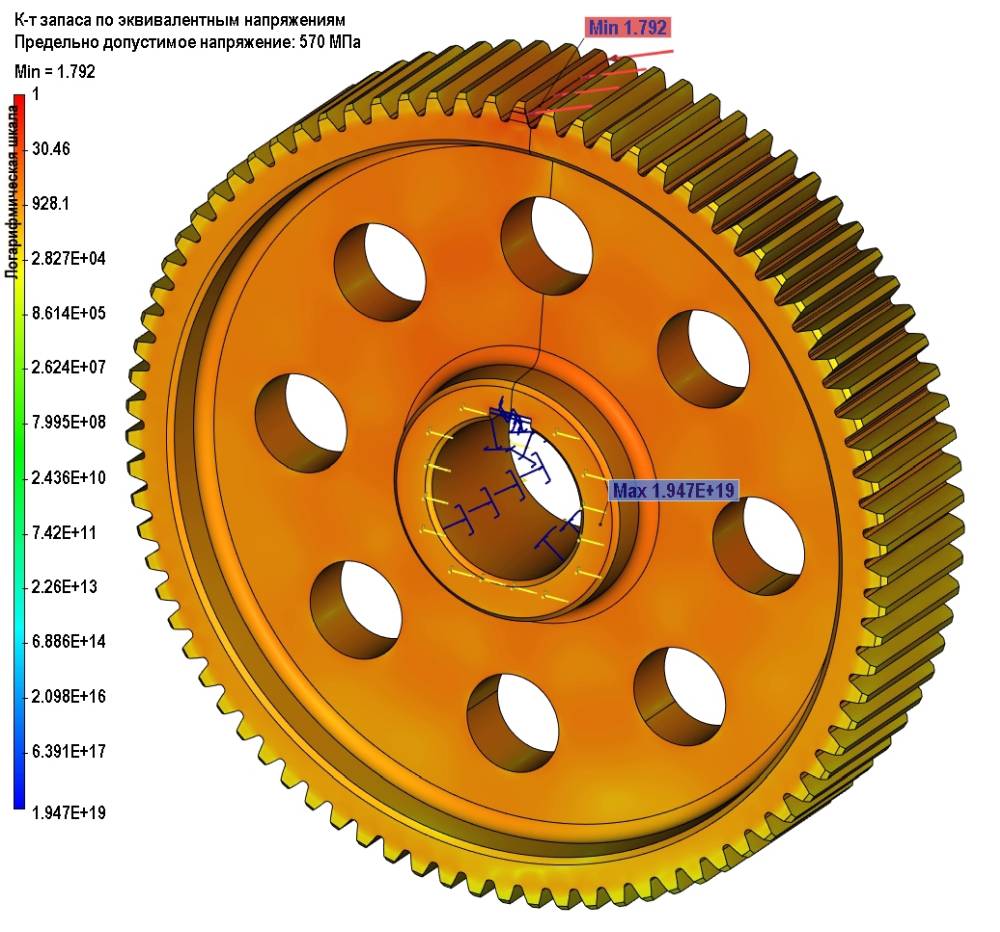
Рис. 10. Запас статической прочности колеса зубчатого

В [8, 9] с помощью модуля T­FLEX Анализ произведены расчеты вала­шестерни и колеса с косозубым внешним эвольвентным цилиндрическим зацеплением. Получены аналогичные данные: шестерня (z1 = 24 шт.) —
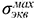= 456,1 МПа, колесо (z1 = 98 шт.) — 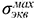= 367,6 МПа, предел текучести стали марки 50 — σm = 530 МПа, модуль mn = 4 мм, ширина колеса bw = 100 мм, полное нормальное усилие Fn = 20649,92 Н. Запас прочности по шестерне составил 1,162.

Также оценены перемещения в зацеплении зубчатых колес (рис. 11), — максимальные перемещения составили 0,05219 мм.

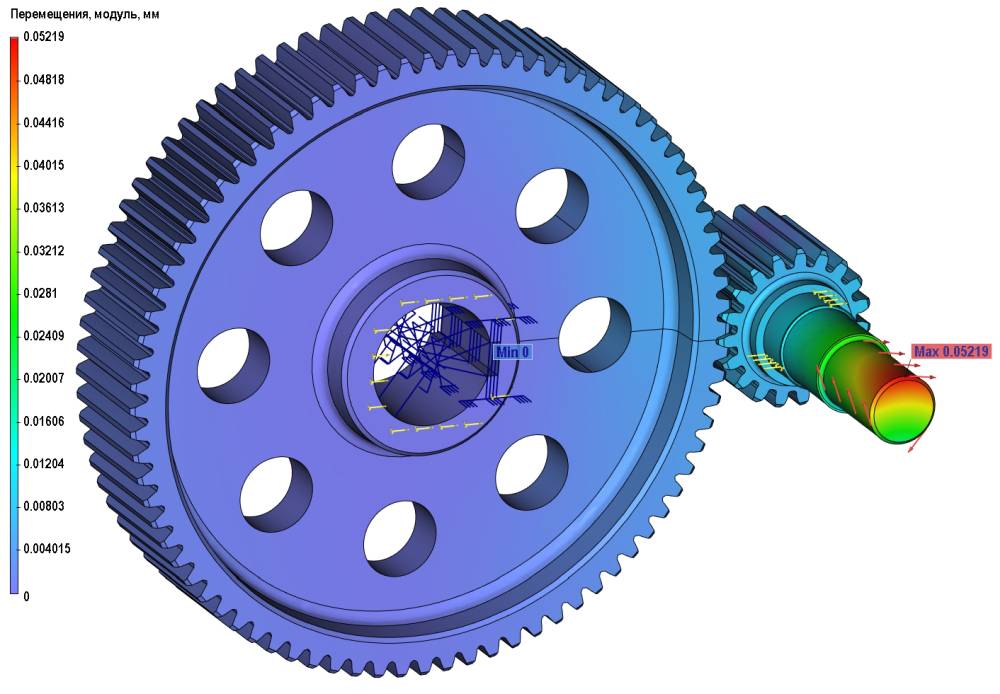
Рис. 11. Перемещения в зубчатой передаче под действием нагрузки

Применение одного из двух методов расчета статической прочности на этапе проектных работ помогает конструктору увидеть наиболее нагруженные места, минимизировать ошибки проектирования и снизить трудозатраты, более рационально подойти к конструированию. Также использование модуля T­FLEX Анализ, встроенного в T­FLEX CAD, позволяет ему произвести полный комплекс всех необходимых расчетов прочности, а кроме того, спроектировать надежный узел с минимальными массово­экономическими затратами в производстве и эксплуатации.

Список литературы:

1. Биргер И.А., Шорр Б.Ф., Иосилевич Г.Б. Расчет на прочность деталей машин: Справочник / 4­е изд., перераб. и доп. М.: Машиностроение, 1993. 639 с.
2. Вельгодская Т.В., Иванов В.В., Гаджиев И.А. Анализ напряженно­деформированного состояния шестерни тягового редуктора локомотива 2ТЭ10Л // Международный научно­исследовательский журнал. 2012. № 5 (5). С. 82­85.
3. Mihailidis A., Korbetis G., Drivakos N., Nerantzis I. Finite Element Method Based Analysis of Planetary Gear Systems Considering Backlash and Manufacturing Deviations. Power Transmission Engineering. June 2018. Р. 46­50.
4. Смагулова А.С., Кияшова А.М. Расчет зубчатых передач с применением конечно­элементного анализа в рамках пакета ANSYS WB // Наука и техника Казахстана. 2018. № 3. С. 39­47.
5. Петренко А.Ф., Бурлакова Д.Е., Савенков В.Н. Напряженное состояние колес зубчатых передач в зоне контакта зубьев // Материалы научной конференции студентов, молодых ученых и преподавателей. 2010. Ч. 1. [Электронный ресурс]. URL: http://masters.donntu.org/2013/fmf/burlakova/library/2.htm (дата обращения: 20.02.2021).
6. Каратушин С.И., Бильдюк Н.А., Плешанова Ю.А., Бокучава П.Н. Проверочный силовой расчет в ANSYS зубчатого зацепления // Известия высших технических заведений. Машиностроение. 2015. № 3 (660). С. 27­34.
7. ГОСТ 21354–87. Передачи зубчатые цилиндрические эвольвентные внешнего зацепления. Расчет на прочность. М.: Изд­во стандартов, 1993. 130 с.
8. Иващенко А.П. Исследование статической прочности косозубого цилиндрического зубчатого колеса // Современные наукоемкие технологии. 2020. № 10. С. 51­56. [Электронный ресурс]. URL: http://www.top­technologies.ru/ru/article/view?id=38254 (дата обращения: 20.02.2021).
9. Иващенко А.П. Исследование статической прочности шестерни, входящей в состав вала­шестерни // Современные наукоемкие технологии. 2020. № 11­1. С. 31­36. [Электронный ресурс]. URL: http://www.top­technologies.ru/ru/article/view?id=38334 (дата обращения: 20.02.2021).
10. T­FLEX CAD Анализ. 2021. [Электронный ресурс]. URL: http://www.tflex.ru/products/raschet/analiz/ (дата обращения 20.02.2021.)