Функциональные кривые высокого качества — инновация в геометрическом моделировании от C3D Labs

Валериян Муфтеев,
к.т.н., ведущий математик-программист C3D Labs

Артем Максименко,
специалист по маркетингу C3D Labs

В современном мире повсеместно востребованы CAD-системы, позволяющие моделировать сложные кривые и поверхности. Эти возможности задействованы при решении многих проектных задач в самых разных областях науки и техники. Однако даже если CAD-система поддерживает моделирование кривых и поверхностей класса А, то она не обеспечивает надлежащего качества так называемых функциональных кривых по критериям плавности.
Перед разработчиками C3D Labs встала задача реализации такого функционала, который позволил бы моделировать кривые линии, а следовательно, и поверхности самого высокого качества. В результате проведенных изысканий в области геометрического моделирования на свет появился C3D FairCurveModeler — новый раздел геометрического ядра C3D Modeler, позволяющий строить кривые класса F.
В данной статье анализируются требования к функциональным кривым, дается описание их преимуществ над другими кривыми, а также приводятся примеры практического применения функционала C3D FairCurveModeler.

Введение в понятие функциональных кривых

Что такое функциональные кривые

К новому типу кривых относятся плоские и пространственные кривые, которые обеспечивают некоторую функциональную характеристику объекта, в связи с чем их целесообразно называть функциональными кривыми [1].

Область применения таких кривых весьма широка и распространяется в основном на проектные задачи, возникающие в разных отраслях техники. Например:

• задача по максимизации подъемной силы при минимизации лобового сопротивления при моделировании профиля крыла самолета (рис. 1);
• задача поиска максимальной плавности трассы при заданных ограничениях для обеспечения комфортной и безопасной езды на транспортном средстве.

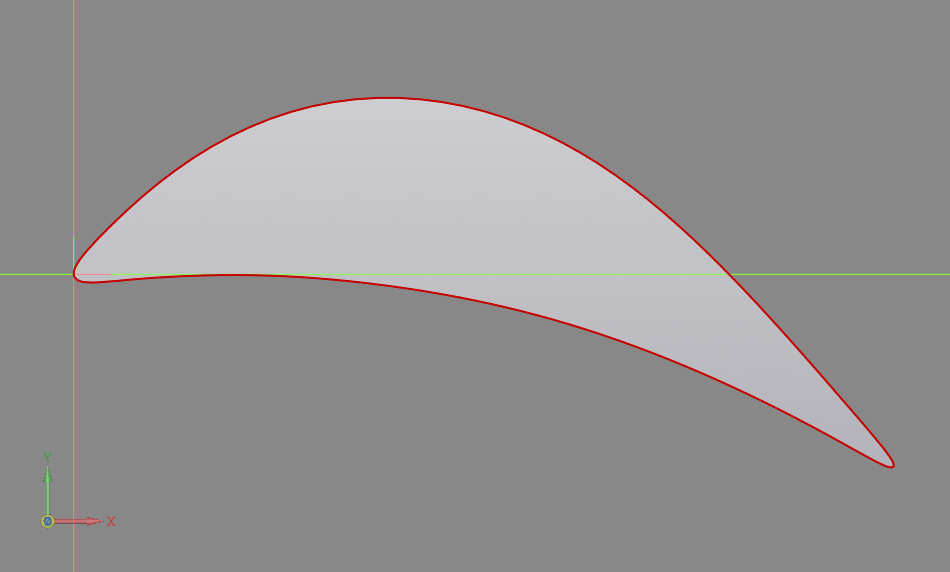
Рис. 1. Испытание профиля крыла в CFD-системе FlowVision

Среди функциональных кривых можно выделить подкласс инженерных аналитических кривых, которые единственным оптимальным образом обеспечивают некоторую проектную характеристику объекта. К таким кривым, например, можно отнести спираль Архимеда, используемую для построения профиля зубьев зубчатого колеса, а также брахистохрону — кривую наискорейшего спуска для транспортировки предметов.

В остальных случаях функциональные кривые имеют свободную форму. Такие кривые могут быть локально­выпуклыми (с постоянным знаком функции кривизны) и иметь точки перегиба (участки с разным знаком функции кривизны).

Кроме того, функциональные кривые могут быть пространственными и, соответственно, иметь кручение.

Рассмотрим подробнее, что представляют собой функциональные кривые и чем они отличаются от обычных гладких кривых.

Требования качества к функциональным кривым

К параметрам плавности рассматриваемых инженерных кривых предъявляются повышенные требования, которые являются универсальными для данного типа кривых и не зависят от специфики проектируемых объектов. Ниже приводится список данных требований с пояснениями.

Высокий, не ниже 4­го, порядок гладкости

Гладкость — это свойство функции или геометрической фигуры (кривой, поверхности и др.), определяющее, дифференцируема ли функция на всем множестве определения или имеется ли у каждой точки данной фигуры окрестность, допускающая задание с помощью дифференцируемых функций.

В различных видах проектирования используются сплайны разного порядка гладкости. Например:

• при моделировании трасс дорог используются клотоидные сплайны, а гладкость обеспечивается не ниже 2­го порядка;
• для профилирования кулачка распределительного вала высокоскоростных двигателей необходима гладкость не ниже 3­го порядка, поэтому проектирование профиля начинается с вычерчивания плавного графика 3­й производной [2];
• при моделировании пространственных кривых для обеспечения непрерывности функции кручения кривая должна иметь 3­й порядок гладкости;
• из анализа пространственной криволинейной траектории движения материальной точки следует, что пространственная кривая с плавным кручением должна иметь 4­й порядок гладкости [3].

Отсутствие или минимальное число экстремумов кривизны

Плавность кривой также зависит от формы графика изменения кривизны вдоль линии движения.

Возвратимся к примеру с материальной точкой. Поскольку осцилляция функции кривизны согласно основному уравнению динамики [3] вызовет пульсацию центробежных сил, действующих на материальную точку, участок линии движения должен иметь минимальное число экстремумов кривизны или вершин кривой.

Наличие лишних экстремумов кривизны, например, у формы технических изделий и объектов дизайна, может вызвать следующие негативные явления:

• неоправданное биение толкателя кулачкового механизма, следствием которого является преждевременный износ механизма;
• залипание почвы на участке плуга с концентрацией кривизны у траектории движения почвы, что приводит к увеличению сопротивления плуга, а следовательно, повышению энергоемкости процесса вспашки (рис. 2) [4];
• при лишних экстремумах кривизны на аэродинамическом профиле возникает неоправданная пульсация среды, обтекающей профиль, что увеличивает его лобовое сопротивление и может спровоцировать срыв потока;
• необходимость лишних торможений и разгонов, что увеличивает энергозатраты на перемещение по трассе транспортного средства [5];
• эффект кривых зеркал у кривых кузовных поверхностей и архитектурных форм [6];
• неправильное визуальное восприятие объектов компьютерной графики и CAD [7].

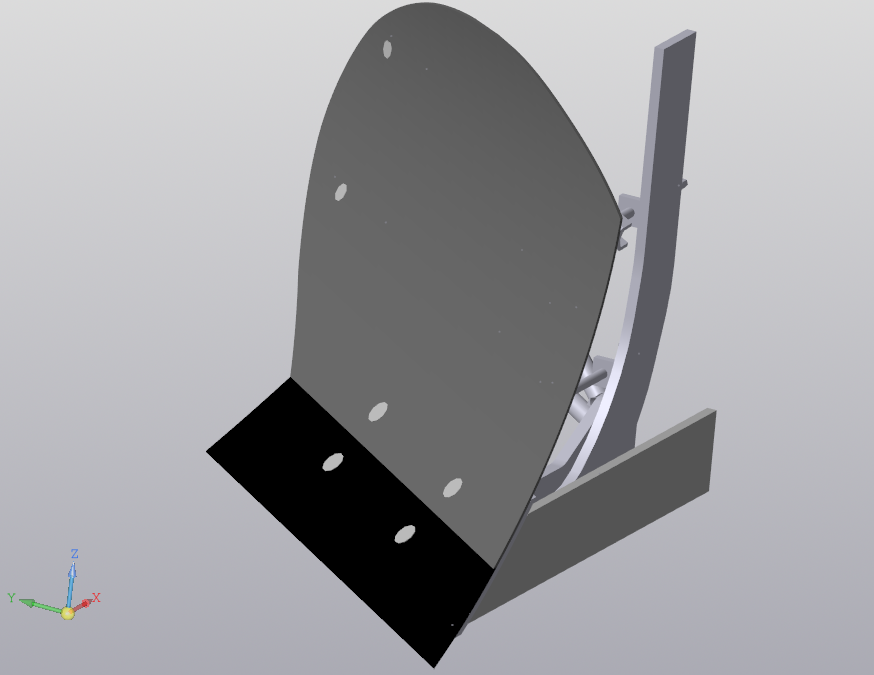
Рис. 2. Сборка плуга в КОМПАС-3D

Малые значения вариации кривизны и скорости ее изменения

В некоторых прикладных областях вводится требование минимизации вариации кривизны, а следовательно, концентрация кривизны должна быть ограничена по максимальному значению.

Например, такое ограничение минимального значения радиуса кривизны (максимальной кривизны) естественным образом вводится при проектировании дорог: минимальный радиус виража ограничивается из расчета допустимой скорости транспортного средства [8, 9].

Важным параметром качества кривой является скорость изменения кривизны. При проектировании трассы дороги этот параметр регламентирует скорость нарастания центробежной силы, действующей на автомобиль на виражах, и легко контролируется благодаря применению сегментов клотоиды с линейным изменением функции кривизны [8, 9].

Малое значение потенциальной энергии кривой

Считается, что плавность кривой напрямую связана с ее потенциальной энергией. Необходимость выбора функциональной кривой с малым значением потенциальной энергии основывается на предположении, что если объект, имеющий функциональную поверхность,  движется с большой скоростью, то среда, обтекающая объект, ведет себя как упругое тело. Очевидно, что для деформации упругой среды по линиям тока с меньшей потенциальной энергией будет затрачиваться меньшая работа. При движении материальной точки по вогнутой криволинейной траектории с учетом трения работа, затрачиваемая на перемещение, будет меньше при меньшем значении потенциальной энергии траектории перемещения [1].

Кривая, имеющая минимальное значение потенциальной энергии, называется эластикой [10]:

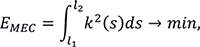
где 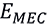— потенциальная энергия кривой;

k(s) — ее кривизна;

l2 и l1— начало и конец интервала.

Эластика может быть представлена в виде осевой линии деформированной упругой рейки между двумя грузиками (ducks). Качество эластик апробировано многовековым опытом судостроения. Гибкие рейки (физические сплайны) применялись для вычерчивания профилей шпангоутов, батоксов и ватерлиний при проектировании и строительстве судов, а позднее — автомобилей и самолетов.

Эстетический анализ кривых

Помимо предложенных выше объективных критериев плавности качество кривой необходимо также оценивать и с позиций законов технической эстетики. Существует такой подход к оценке эстетичности кривой, когда форма кривой базируется на математических характеристиках форм, выявленных у объектов реального мира (например, очертания крыльев бабочек) [11, 12].

Для моделирования красивых (эстетических) форм предлагаются так называемые log­эстетические кривые, имеющие линейный график кривизны в логарифмической шкале [13­15]. Множество известных спиралей, в том числе клотоида, являются частными случаями кривых этого класса. В работе [16] был предложен наиболее обобщенный класс кривых с монотонной функцией кривизны, называемый суперспиралями. Уравнения этих кривых выражаются через Гауссовы гипергеометрические функции и численно интегрируются адаптивными методами типа метода Гаусса — Кронрода.

Однако множество эстетических кривых не ограничивается только множеством log­эстетических кривых. Кривые могут иметь произвольно сложные плоские и пространственные формы и быть вполне эстетичными.

Авторы работы считают, что приоритетной является оценка по критериям плавности. Экспертная оценка с позиций законов технической эстетики (лаконичность, целостность, выразительность, пропорциональная согласованность, композиционное равновесие, структурная организованность, образность, рациональность, динамичность, масштабность, пластичность, гармоничность) правомерна только после оценки на плавность.

Весьма показательна в этом смысле работа [17], в которой приводятся графики экспертной оценки эстетического качества кривых с различными параметрами плавности (рис. 3). Наиболее высокая экспертная оценка у кривых, которые отвечают базовым требованиям к функциональным кривым (одновременно малое значение кривизны и малая скорость изменения кривизны).

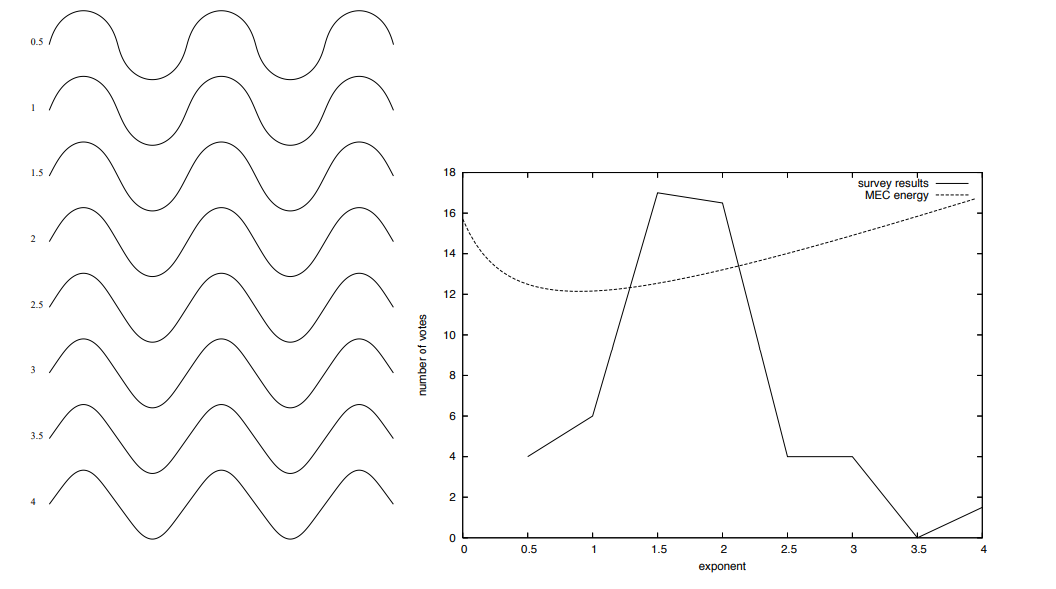
Рис. 3. Тест из работы Levien’а (2009)

Промежуточные итоги

С учетом всех вышеупомянутых требований для построения очень плавной траектории движения необходимы:

• минимальное число опорных точек моделируемой сплайн­траектории движения и высокий, не ниже 4­го, порядок гладкости;
• плавное кручение пространственной кривой;
• ограничение максимального значения кривизны и скорости ее изменения;
• минимизация функционала потенциальной энергии.

Функциональные кривые, параметры которых соответствуют приведенным требованиям, называются кривыми класса F [1].

Для сравнения здесь важно отметить, что именно эти жесткие требования к параметрам плавности и отличают кривые данного класса от кривых класса A. Последние являются формообразующими поверхностей класса А — высококачественных по критериям эстетики поверхностей внешних кузовных поверхностей. «Хорошая» кривая для этих поверхностей будет иметь график кривизны с небольшим числом участков монотонного изменения кривизны [18]. Данное требование можно сравнить с требованием минимальности количества экстремумов кривизны у функциональных кривых.

Таким образом, кривые класса А представляют собой кривые для формообразования поверхностей в промышленном дизайне (рис. 4), в то время как функциональные кривые являются инженерными кривыми. Такие кривые высокого качества также принято называть плавными кривыми (faired curves, fairing curves). Здесь важно не путать последние с гладкими кривыми, которые являются кривыми самого низкого качества — первого порядка гладкости [19].

Рис. 4. Модель снегохода

Реализация методов F­кривых в C3D Modeler

Что такое C3D FairCurveModeler

C3D FairCurveModeler — это библиотека моделирования плавных кривых, реализованная как совершенно новый раздел геометрического ядра C3D Modeler, расширяющий его возможности для поверхностного моделирования.

Кривые класса F, описанные ранее, моделируются с помощью методов C3D FairCurveModeler. Помимо возможности построения кривых высокого качества по критериям плавности методы также удовлетворяют следующим требованиям:

• устойчивость формообразования, или изогеометричность;
• инвариантность относительно аффинных и проективных преобразований;
• гибкость;
• инструментальное разнообразие;
• возможность изогеометрической аппроксимации аналитических кривых с сохранением их базовых свойств.

Функционал C3D FairCurveModeler описывается с помощью терминов инженерной геометрии. Модель кривой в инженерной геометрии называется определителем [20] и состоит из геометрической части и алгоритма генерации точек кривой или процедуры построения аппроксимирующего сплайна. Геометрическую часть определителя можно рассматривать как геометрический определитель кривой. Наиболее привычными и естественными видами геометрического определителя являются множества точек (вида опорной ломаной) или множества касательных прямых (в частности, вида касательной ломаной). Кроме того, в инженерной геометрии используются так называемые управляющие сплайновые полигоны NURBS­кривых.

Различные виды геометрических определителей имеют свои достоинства и недостатки. Ломаная инцидентности позволяет точно позиционировать кривую, касательная ломаная однозначно и точно задает форму моделируемой кривой, S­полигон NURBS­кривой высокой степени позволяет локально изменять форму кривой и гарантирует высокое качество пространственных кривых по критериям плавности кривизны и кручения.

В библиотеке C3D FairCurveModeler используется также уникальный геометрический определитель — геометрический определитель Эрмита (ГО Эрмита) второго порядка фиксации. ГО Эрмита представляет собой опорную ломаную, оснащенную в каждой своей вершине касательным вектором и вектором кривизны.

Фундаментальные основы C3D FairCurveModeler

Ниже приводятся четыре фундаментальных «открытия», ставшие отправной точкой в разработке функционала моделирования плавных кривых:

1 Теоретическим фундаментом, или первым «краеугольным камнем», C3D FairCurveModeler является теория параметризации, или теория исчисления параметров. На ее основе было обобщено понятие сплайна как множества базовых кривых, имеющих совпадающие геометрические параметры в произвольных точках опорной ломаной. В традиционных сплайнах базовые кривые имеют совпадающие параметры только в точках стыка сегментов сплайна.

Первым открытием является метод определения базиса сплайна как множества конических кривых двойного соприкосновения на локально­выпуклой опорной ломаной (рис. 5).

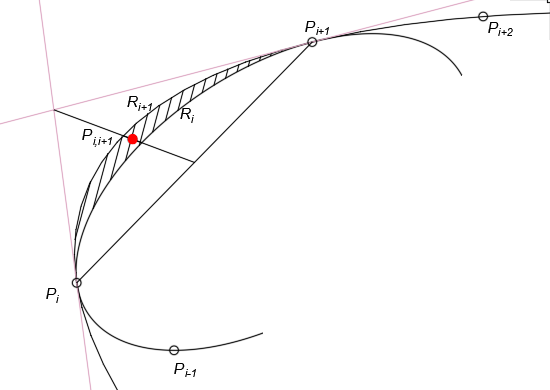
Рис. 5. Конические кривые двойного соприкосновения

Смежные кривые образуют на общем сегменте ломаной «линзу». Напряженность сплайна характеризуется величиной отклонения смежных аналитических кривых базиса сплайна и визуально легко оценивается по величине линзы между смежными кривыми.

2 Вторым «краеугольным камнем» фундамента является алгоритм генерации точек виртуальной кривой (V­кривой) на базисе сплайна дискретного множества конических кривых двойного соприкосновения. Метод V­кривой разработан в C3D Labs в рамках приведенного выше подхода.

Точки кривой генерируются в области линз, что уменьшает напряженность сплайна, построенного на сгенерированных точках. Затем на множестве сгенерированных точек вновь определяется множество конических кривых двойного соприкосновения. Последовательность этих операций в пределе определяет виртуальную кривую класса C5 [21].

Виртуальная кривая (V­кривая) обладает рядом замечательных свойств:

• минимальным числом экстремумов кривизны;
• дуальностью (как и коническую кривую, V­кривую можно определять не только на опорных точках, но и на касательных);
• аффинной инвариантностью;
• малой чувствительностью к распределению точек на контуре кривой.

Важным следствием этих свойств является возможность геометрически точного моделирования конических кривых.

3 Третий «краеугольный камень» — изогеометрическая аппроксимация виртуальной кривой посредством рациональной сплайновой кривой Безье (NURBzS­кривой) — один из геометрически ориентированных методов изогеометрического построения NURBS­кривой.

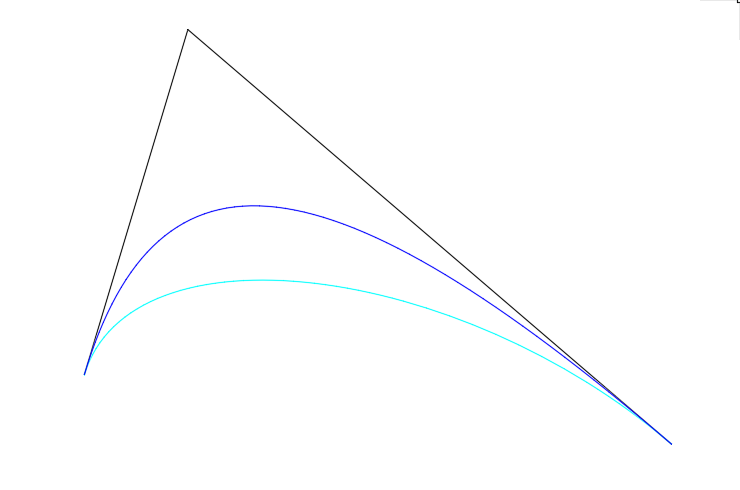
Рис. 6. Конические кривые двойного соприкосновения

Графоаналитический алгоритм состоит из следующих простых операций:

а) конические кривые двойного соприкосновения на общем сегменте опорной ломаной рассматриваются как кривые Безье 2­й степени с B­полигонами в виде двухзвенников (рис. 6);

б) у кривых Безье повышается степень до 3­й (рис. 7) с B­полигонами в виде трехзвенников;

Рис. 7. Преобразование конических кривых до рациональных кривых Безье 3-й степени

в) результирующий B­полигон получается усреднением исходных B­полигонов. Среднее звено результирующего B­полигона параллельно исходным и лежит на равном расстоянии от них (рис. 8).

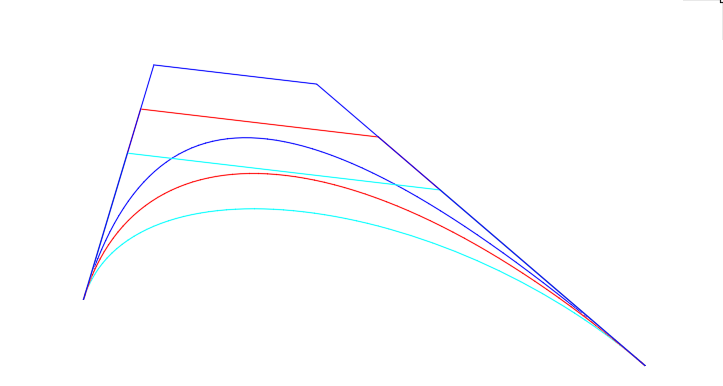
Рис. 8. Построение результирующего B-полигона

Поскольку усредненный B­полигон также будет выпуклым, как и исходные B­полигоны, обеспечивается строгая изогеометричность;

г)  уточняются значения кривизны в концевых точках результирующей кривой по значениям исходных кривых.

Алгоритм имеет модификацию. При резких изменениях кривизны, когда одно значение близко к нулевому, B­полигон корректируется таким образом, что кривая Безье, определенная на скорректированном B­полигоне, имеет более точную меньшую кривизну.

4 Четвертый «краеугольный камень» — изогеометрическая аппроксимация виртуальной кривой посредством B­сплайновой кривой.

Ключевым моментом здесь является отказ от традиционного подхода, при котором считается, что опорные точки должны совпадать с узловыми точками сплайна. Сплайн должен проходить через точки опорной ломаной, но узлы сплайна (или любые точки сплайна с фиксированными значениями внутреннего параметра) не совпадают с вершинами опорной ломаной.

Алгоритм является эвристическим — аналогом ручного редактирования S­полигона. Для построения используются исходные касательные прямые в точках V­кривой. Пересечения касательных прямых определяют вершины S­полигона (рис. 9).

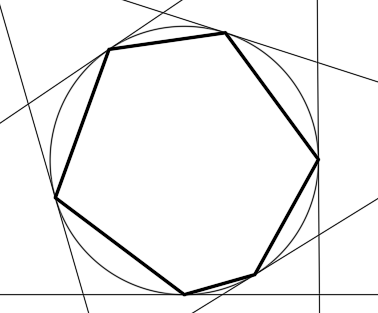
Рис. 9. ГО Эрмита первого порядка фиксации

На S­полигоне в текущей итерации вычисляются расстояния от точек до сплайна. Касательная прямая параллельно себе перемещается на величину невязки  в сторону уменьшения невязки (рис. 10).

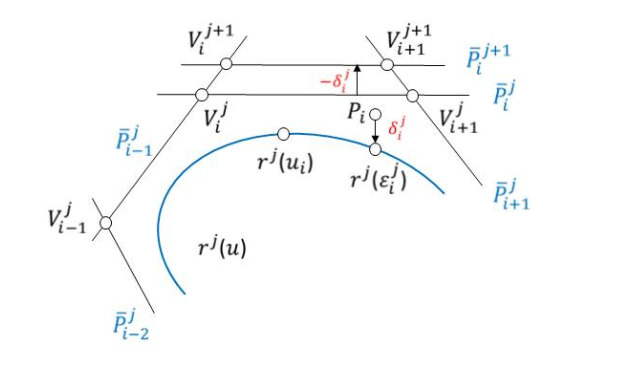
Рис. 10. Итерация приближения сплайна

Затем итерация повторяется. Приведенный алгоритм изогеометрической аппроксимации является типичной эвристической графоаналитической процедурой.

Методы построения кривых C3D FairCurveModeler

Далее приводится описание алгоритмов работы методов C3D FairCurveModeler для моделирования кривых высокого качества различной формы.

Моделирование кривых сложной формы

Исходный ГО кривой сложной формы структурируется, определяются точки перегиба. По точкам перегиба исходный ГО разбивается на ряд локально­выпуклых участков. На каждом локально­выпуклом участке строится виртуальная кривая (V­кривая). При определении V­кривой на участке ломаной с концевой точкой, принадлежащей точке перегиба, задается нулевое значение кривизны в концевой точке.

Моделирование кривых пространственной формы

Исходная пространственная ломаная развертывается на плоскости таким образом, что сохраняются длины звеньев и углы между звеньями. Затем ломаная структурируется и определяется V­кривая.

Для сглаживания прерывистого кручения пространственной NURBzS­кривой выполняется следующая процедура, привязанная к команде повышения степени.

Степень кубической NURBzS­кривой повышается до шестой. Сегмент NURBzS­кривой имеет B­полигон с семью вершинами. У смежных сегментов определяются соприкасающиеся в концевых точках плоскости. Эти плоскости определяются тремя концевыми точками B­полигонов. У смежных сегментов определяется биссекторная плоскость к двум смежным соприкасающимся плоскостям. Третьи вершины B­полигонов, считая от общей точки, проецируются на биссекторную плоскость.

Моделирование B­сплайновой поверхности высоких степеней

В функционал C3D FairCurveModeler не требуется добавления методов для построения и редактирования B­сплайновых поверхностей, поскольку для этого используются только методы построения B­сплайновых кривых.

Каркасно­кинематическое представление B­сплайновой поверхности, принятое в инженерной геометрии, позволяет разбить процесс построения поверхности на два этапа:

1 Первый этап — построение образующих B­сплайновых кривых с применением V­кривых (рис. 11 и 12);

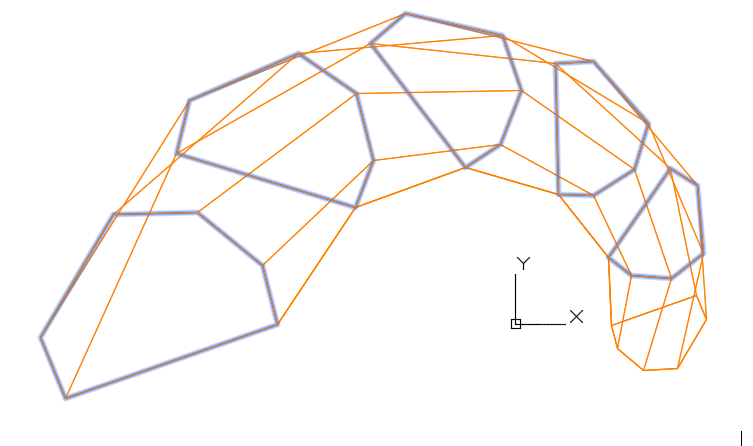
Рис. 11. Исходная сеть опорных точек

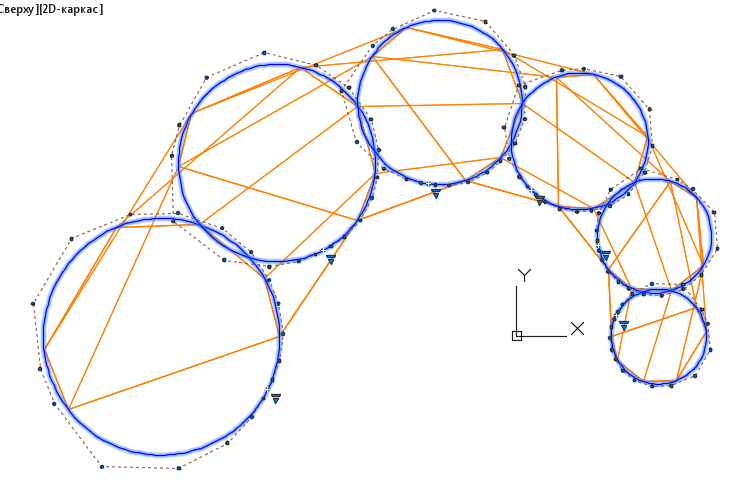
Рис. 12. Каркас S-полигонов образующих B-кривых

2 Второй этап — построение направляющих B­сплайновых кривых с применением V­кривых (рис.13 и 14).

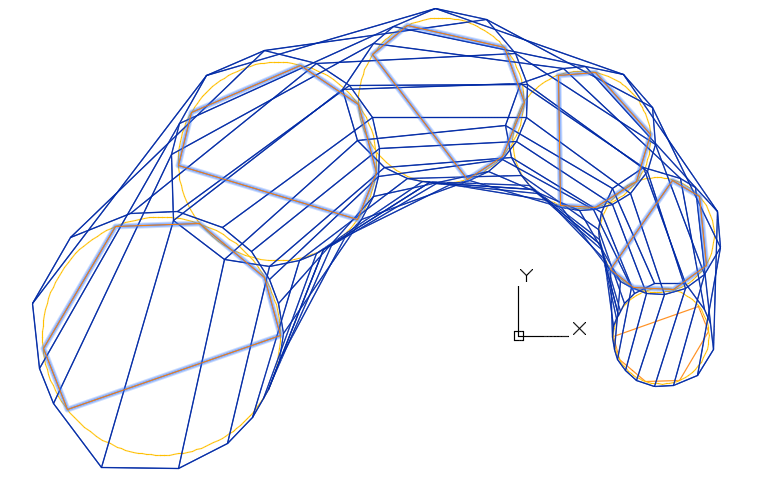
Рис. 13. Сеть S-полигонов образующих B-кривых

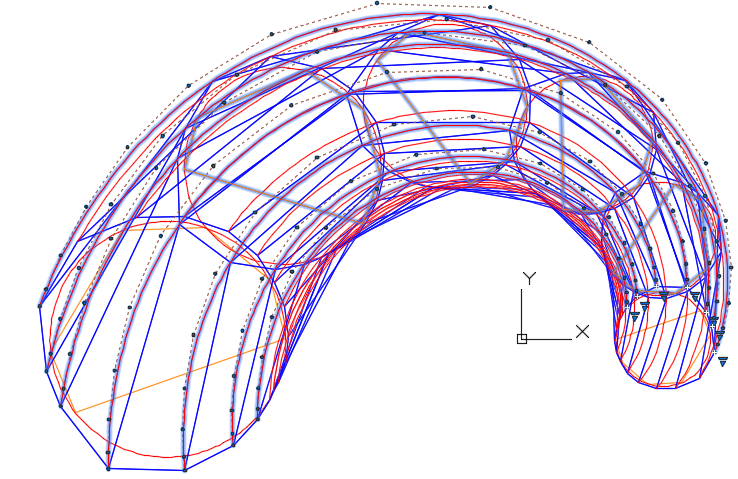
Рис. 14. Каркас S-полигонов формирует S-фрейм B-сплайновой поверхности

Практическое применение С3D FairCurveModeler

Немного о сфере применения

В заключительном блоке статьи приведены примеры практического применения C3D FairCurveModeler при моделировании различных изделий. Применение данного раздела C3D в области моделирования изделий — это быстрый и недорогой способ улучшения проектных характеристик, поскольку качество проектируемого изделия можно существенно повысить только за счет улучшения плавности его геометрии.

Обычно при оптимизации конструкции берется некоторый приоритетный параметр, который минимизируется/максимизируется, при этом остальные параметры ухудшаются. Грамотная оптимизация заключается в том, чтобы остальные параметры остались в пределах некоторых ограничений.

Опыт практического использования С3D FairCurveModeler

Моделирование плуга

При оптимизации конструкции плуга для повышения качества вспашки на плуг монтируются так называемые акульи плавники, которые способствуют более качественному рыхлению почвы, но при этом неминуемо растет сопротивление плуга, а следовательно, растут расходы на горючее для трактора.

Для проведения опыта по оптимизации использовалась стандартная конструкция плуга, а изменениям подвергалась только его геометрия, при этом был получен парадоксальный положительный результат. По критериям плавности была улучшена направляющая кривая плуга и оптимизирована схема построения беззадирной поверхности плуга [22].

Конструкция плуга прошла тщательное тестирование в CFD­системе FlowVision компании ТЕСИС, а затем тестирование на почвенном канале и полевые испытания, которые показали положительный результат: одновременно было улучшено качество вспашки и сэкономлено топливо [23]!

Моделирование кулачков

При моделировании профилей плоских кулачков необходимо решить две проблемы:

1. Кривые выстоя толкателя должны геометрически точно совпадать с окружностями.
2. Переходные кривые подъема и опускания должны спрягаться с кривыми выстоя с порядком гладкости не менее 3­го, во избежание так называемого рывка (Jerk).

Методы C3D FairCurveModeler решают эти проблемы, то есть обеспечивают построение кривых, геометрически точно моделирующих конические кривые, а также возможность построения переходных кривых до 9­го порядка гладкости.

Конструктору остается только правильно построить эти кривые надлежащей формы, обеспечивающей необходимую функцию газораспределения.

Моделирование профиля лопатки

В C3D Labs был проведен небольшой эксперимент, в ходе которого удалось установить, какие преимущества дают функциональные кривые при моделировании промышленных изделий на примере профиля лопатки паровой турбины. В ходе эксперимента геометрия лопатки была улучшена, а исправленная модель испытана в CFD­приложении KompasFlow для CAD­системы КОМПАС­3D. При оптимизации лопатки была применена та же схема, что и при оптимизации конструкции плуга.

Все профили лопаток стандартизованы и объединены в базу данных отрасли. Стандартные профили являются результатом колоссальной работы по оптимизации макропараметров лопатки и входят в золотой фонд паротурбиностроения.

Тот же подход был применен к оптимизации геометрии изделия. В рамках заданных макропараметров улучшалась только геометрия лопатки.

Профиль лопатки представляет собой сложную кривую, составленную из дуг окружностей (рис. 15 и 16).

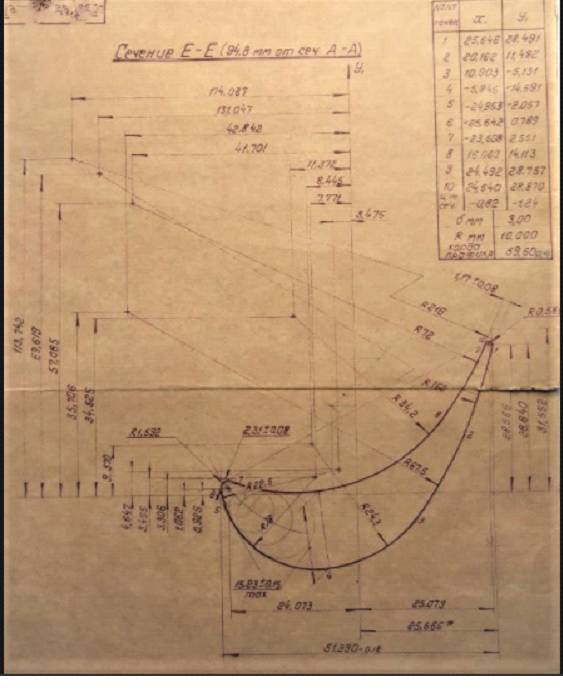
Рис. 15. Чертеж профиля лопатки

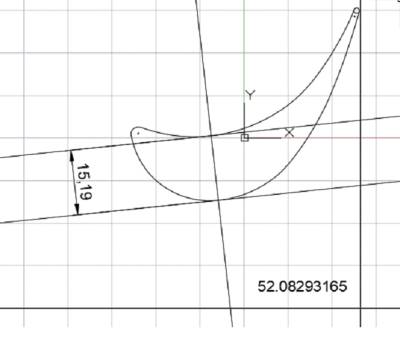
Рис. 16. Чертеж профиля лопатки в CAD-системе

На основе данного контура была подготовлена модель для обдува в KompasFlow. Направление входного потока совпадает с биссектрисой угла входного клина лопатки (рис. 17).

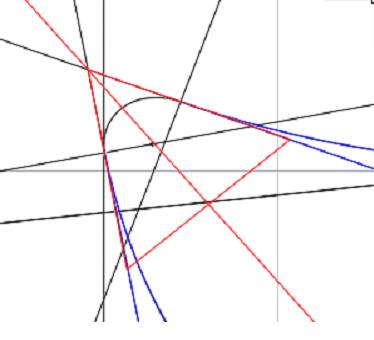
Рис. 17. Входной клин лопатки

Поскольку в венце работает не отдельная лопатка, в модель включены зазоры между лопатками и контуры смежных лопаток. Шаг между лопатками принят в 20 мм (рис. 18­20).

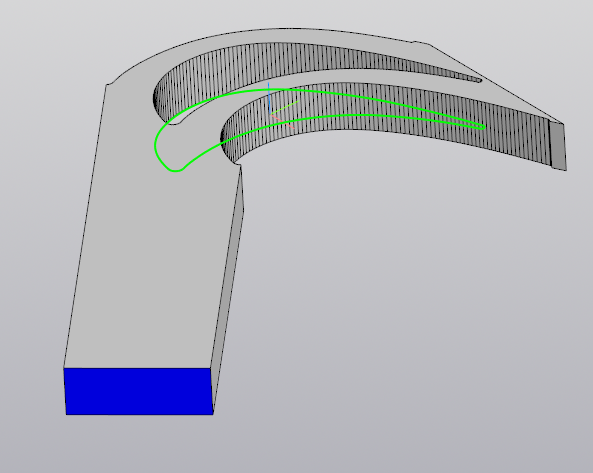
Рис. 18. 3D-модель для симуляции обдува лопаток. Грань для входа жидкости (синего цвета)

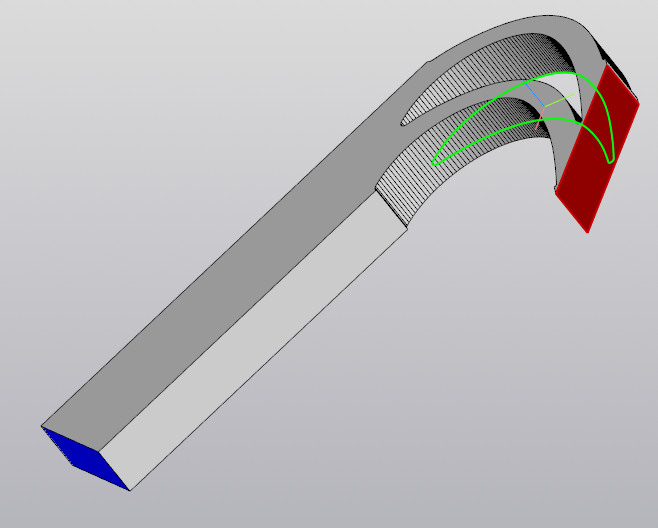
Рис. 19. Грань для выхода потока жидкости (голубого цвета)

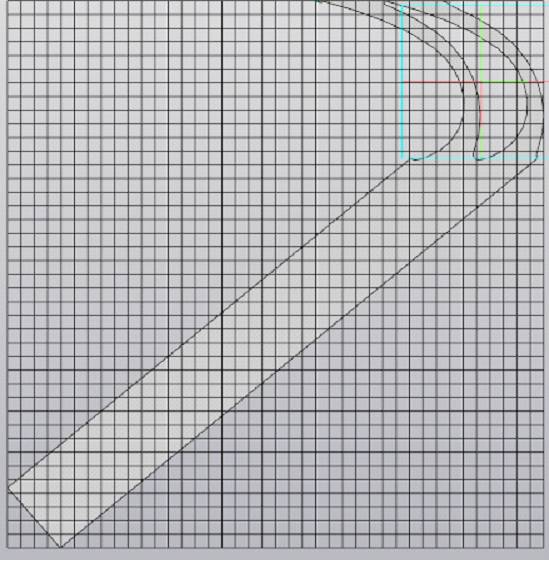
Рис. 20. Расчетная сетка с адаптацией

Для визуального отображения параметров введены вспомогательные плоскости. Горизонтальная плоскость на расстоянии 5 мм от OXY для отображения векторов скоростей и вспомогательная плоскость, совпадающая с гранью выхода потока, для фиксации результатов. Введены параметры результата: средняя скорость и общее давление (рис. 21).

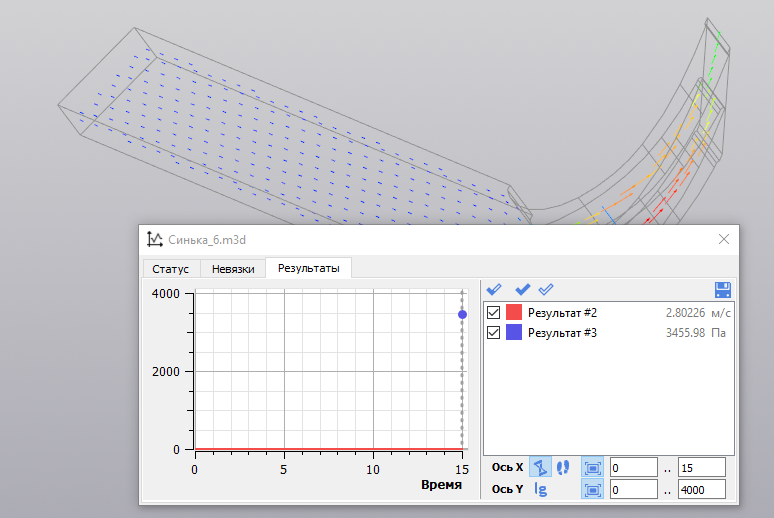
Рис. 21. Расчетные параметры

В результате работы KompasFlow были получены следующие значения параметров:

• средняя скорость на выходе — 2,80226 м/с;
• общее давление на выходе — 3455,98 Па.

Можно предположить, что улучшение плавности контура лопатки при сохранении исходных макропараметров улучшит и проектные параметры контура.

Перестроим кривые спинки и корыта с использованием функций построения кривых высокого качества по критериям плавности геометрического ядра C3D (раздел FairCurveModeler) — рис. 22.

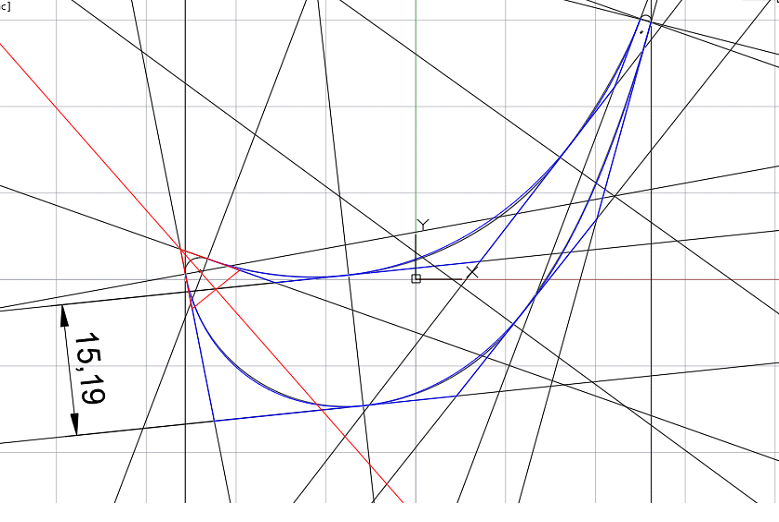
Рис. 22. Касательные ломаные синего цвета и построенные кривые синего цвета на касательных ломаных. Исходные кривые — черного цвета

В точках стыка дуг были построены касательные и перестроены кривые профилей с помощью команды построения V­кривой на касательной ломаной. Профили имеют плавные графики кривизны (рис. 23 и 24).

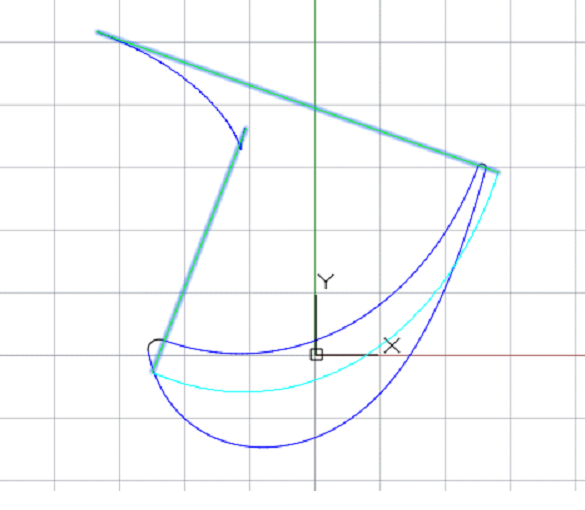
Рис. 23. График кривизны «корыта» лопатки

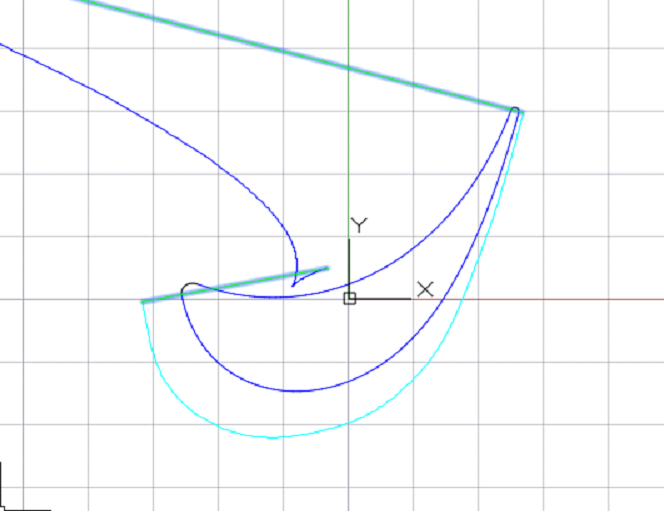
Рис. 24. График кривизны «спинки» лопатки

Для испытаний была использована та же 3D­модель. В эскизе кривые спинки лопатки и корыта лопатки были заменены на новые кривые. Параметры расчета остались те же (рис. 25).

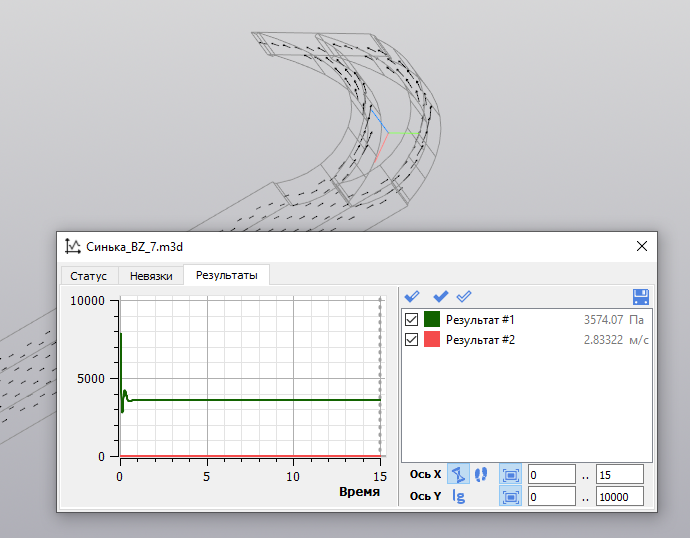
Рис. 25. Результаты испытания контура лопатки с улучшенными кривыми

Пространство лопатки в венце с улучшенными кривыми обеспечивает лучшие параметры: оно разгоняет поток до скорости 2,83322 м/с с общим давлением 3574,07 Па.

Эти параметры превышают параметры исходного контура (средняя скорость на выходе 2,80226 м/с, общее давление на выходе 3455,98 Па).

Подводя итоги эксперимента, необходимо отметить, что сравнительные испытания в системе KompasFlow показали ощутимое улучшение проектных характеристик венца турбины, благодаря реализации схемы улучшения плавности контура лопатки с помощью методов геометрического ядра C3D (раздел FairCurveModeler). Указанное обстоятельство, как и рассмотренные выше иные примеры моделирования геометрии изделий, свидетельствует о том, что принцип улучшения проектных характеристик изделия за счет улучшения геометрии функциональных кривых имеет огромный потенциал.

Окончательные итоги

Функционал нового раздела C3D Modeler C3D FairCurveModeler позволяет моделировать плавные кривые, которые являются кривыми высокого качества и отвечают жестким требованиям гладкости и эстетики, предъявляемым к инженерным кривым.

На основании примеров, демонстрирующих практическое применение функционала ядра, можно с уверенностью сказать, что C3D FairCurveModeler обладает большим потенциалом применения в области моделирования промышленных изделий, так как позволяет существенно повысить их проектные характеристики достаточно недорогим и простым способом — улучшением геометрии.

Библиографический список:

1.     Муфтеев В.Г., Мударисов С.Г., Фархутдинов И.М. и др. Обоснование выбора оптимальной формы функциональной кривой динамической поверхности технического изделия // Известия международной академии аграрного образования, 2013. Вып. 17. С. 90­93.
2.     Рожков А.П. Кулачок привода клапана. Авторское свидетельство № 1237778, приоритет от 5 сентября 1983 г., зарегистрирован 15 февраля 1986 г., с 1 июля 1991 г. выдан патент взамен авторского свидетельства.
3.     Карякин Н.И., Быстров К.Н., Киреев П.С. Краткий справочник по физике. М.: Высшая школа, 1969. 600 с.
4.     Муфтеев В.Г., Мударисов С.Г., Марданов А.Р. Моделирование рабочей поверхности плуга // Материалы Всероссийской научно­практической конференции, посвященной 75­летию со дня открытия Чувашской государственной сельскохозяйственной академии. Чебоксары: Изд­во ЧГСА, 2006. С. 479­482.
5.     Абдуллин М.М., Фаттахов М.М., Федоров П.А. Архитектурно­ландшафтное проектирование дорог с учетом дорожной геометрии: Учебник. Уфа: Нефтегазовое дело, 2011. 320 с.
6.     Фокс А., Пратт М. Вычислительная геометрия. Применение в проектировании и на производстве: Пер. с англ. М.: Мир, 1982. 304 с., ил.
7.     Ziatdinov R. Visual Perception, Quantity of Information Function and the Concept of the Quantity of Information Continuous Splines // Scientific Visualization. 2016. No 8. Vol. 1. P. 168­178.
8.     Андреев О.В., Бабков В.Ф. Справочник инженера­дорожника. 2­е изд., перераб. и доп. М.: Транспорт, 1969. 552 с.
9.     Справочная энциклопедия дорожника / Минтранс России, Росавтодор. Т. 5. Проектирование автомобильных дорог // Под ред. Г.А. Федотова, П.И. Поспелова. М.: Информавтодор, 2007. 815 с.
10.     Shen, J., Kang, S. H., Chan, T. F. Euler’s elastica and curvature­based inpainting // SIAM Journal on Applied Mathematics. 2003. No 63. Vol. 2. P. 564­592.
11.     Kineri, Y., Endo, S., Maekawa, T. Surface design based on direct curvature editing // Computer­Aided Design. 2014. Vol. 55. P. 1­12.
12.     Harada, T. Study of quantitative analysis of the characteristics of a curve // Forma. 1997. Vol. 12. No. 1. P. 55­63.
13.     Yoshida, N., Saito, T. Interactive aesthetic curve segments // The Visual Computer. 2006. No. 9. Vol. 22. P.  896­905.
14.     Gobithaasan, R.U., Miura, К.T. Aesthetic Spiral for Design // Sains Malaysiana. 2011. Vol. 40. No. 11. P. 1301­1305.
15.     Inoguchi, J. Attractive plane curves in differential geometry. In Mathematical Progress in Expressive Image Synthesis, 3rd ed. // Mathematics for Industry. Springer: Singapore, 2016. Vol. 24. P. 121­135.
16.     Ziatdinov, R. Family of superspirals with completely monotonic curvature given in terms of Gauss hypergeometric function // Computer Aided Geometric Design. 2012. Vol. 29. No. 7. P. 510­518.
17.     Levien, R. L. From Spiral to Spline: Optimal Techniques in Interactive Curve Design. PhD.thesis, University of California, Berkeley, 2009.
18.     Farin, G. Class A Bézier curves // Computer Aided Geometric Design. 2006. No. 23.
19.     Погорелов А.В. Геометрия. М.: Наука, 1983. 288 с.
20.     Муфтеев В.Г. Конструирование криволинейных поверхностей на основе метода огибающей и параметрических В­сплайнов: Дис. ... канд. техн. наук. Киев, 1986. 274 с.
21.     Муфтеев В.Г. Конструирование плоских кривых методом огибающей // Изв. вузов. Авиационная техника. 1980. № 4. С. 43­47.
22.     Мударисов С.Г., Муфтеев В.Г., Фархутдинов И.М. Оптимизация геометрии лемешно­отвальной поверхности плуга / Механизация и электрификация сельского хозяйства. 2009. № 4. С.17­19.
23.    Фархутдинов И.М. Совершенствование лемешно­отвальной поверхности корпуса плуга на основе моделирования технологического процесса вспашки. 05.20.01 — Технологии и средства механизации сельского хозяйства. Диссертация на соискание ученой степени канд. техн. наук. Научный руководитель доктор технических наук профессор С.Г. Мударисов.