Возможная реализация геометрических преобразований в CAD-системах

Алексей Бойков,
старший преподаватель кафедры инженерной графики РТУ МИРЭА, в 2004 году окончил ИГЭУ по специальности «Программное обеспечение вычислительной техники и автоматизированных систем»

Введение

Создание геометрических моделей различных технических поверхностей до сих пор остается актуальной проблемой, поскольку современные CAD-системы позволяют автоматизировать создание моделей лишь для ограниченного набора поверхностей (варианты кинематических поверхностей). В общем же случае требуется находить достаточное число точек или линий каркаса поверхности, что может потребовать большого числа «ручных» построений или привлечения аппарата аналитической геометрии (вывод уравнений и формул) и средств программирования.

В настоящей публикации делается попытка спроектировать работу инструментов геометрических преобразований как одного из способов «мгновенного» образования технических поверхностей, как если бы они уже имелись в CAD-системе.

Применение геометрических преобразований в конструировании

Геометрические преобразования в настоящее время являются основой выделения «геометрий» — разделов в рамках общей геометрической науки, посвященных изучению свойств фигур, инвариантных относительно того или иного преобразования. Например, Евклидова (метрическая) геометрия изучает свойства фигур, которые сохраняются при сдвиге, поворотах, отражении и подобии, аффинная — при аффинных преобразованиях, проективная — проективных и т.п. Применение геометрических преобразований в конструировании разнообразно (рис. 1): проектирование плоских и пространственных механизмов, моделирование аэродинамических профилей и динамических каналовых поверхностей, сложных поверхностей в судостроении и архитектуре ([1-9] и др.).

Рис. 1. Применение нелинейных преобразований: а — проектирование механизма [2], б — аэродинамического профиля [5], в — каналовой поверхности [6], г — архитектурной оболочки [7], д — судовой поверхности [8]

Наибольшее распространение получили проективные преобразования, инверсия, кремоновы (бирациональные), некоторые топологические преобразования.

Инструменты геометрических преобразований в САПР КОМПАС-3D

В CAD-системах среди инструментов геометрические преобразования представлены очень ограниченно. Рассмотрим, например, инструменты САПР КОМПАС-3D:

• на плоскости:
  • команды Переместить по координатам, Копия указанием, Повернуть, Копия по сетке, Копия по кривой, Копия по окружности, Копия по концентрической сетке, Зеркально отразить реализуют преобразования метрической группы: сдвиг, поворот и осевую симметрию,
  • команды Масштабировать, Копия по сетке, Копия по концентрической сетке реализуют преобразование равномерного сжатия/растяжения (гомотетию) метрической группы,
  • команда Масштабировать при различных коэффициентах по осям x и y реализует (ограниченно — например, не может применяться к окружностям) неравномерное сжатие/растяжение аффинной группы;
• в пространстве:
  • команды Изменить положение, Масштабировать и Массив по… реализуют сдвиг, поворот и равномерное сжатие/растяжение метрической группы,
  • команды Элемент выдавливания, Элемент вращения, Элемент по траектории (и, соответственно, — Вырезать…, Поверхность…) реализуют сдвиг и поворот образующих линий в процессе формирования тел и поверхностей.

Легко заметить, что стандартные инструменты не только не реализуют возможностей нелинейных преобразований, но даже не позволяют выполнить преобразования проективной группы. Сказанное справедливо и в отношении геометрических редакторов других «легких» и «средних» САПР.

Реализация геометрических преобразований той или иной фигуры на плоскости или в пространстве вручную заключается в многочисленном повторении построений. Например, чтобы выполнить инверсию окружности, требуется выполнить инверсию трех ее точек, а затем построить окружность по трем точкам (рис. 2а). Чтобы выполнить инверсию эллипса, потребуется выполнить инверсию множества точек и соединить их сплайном, так как кривая 4-го порядка, появляющаяся в результате, может быть представлена в САПР КОМПАС-3D только после аппроксимации сплайном (рис. 2б).

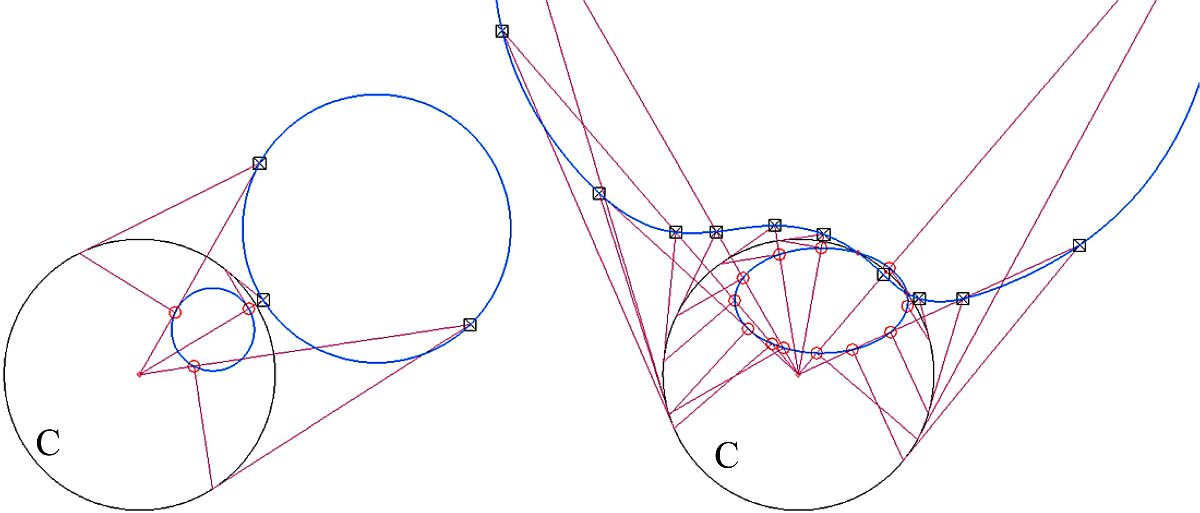
Рис. 2. Инверсия окружности и эллипса (показан фрагмент)

Недостаточно даже знать формулы преобразования: так, в САПР КОМПАС-3D можно задать кривую уравнениями, но, чтобы получить уравнения преобразованной кривой, потребуется сначала узнать уравнение исходной кривой (как правило, полученной в ходе построений, чаще всего — составной).

Поэтому на практике оказывается проще тем или иным способом автоматизировать построения, которые реализуют преобразование, применить их к достаточному числу точек фигур и получить модели преобразованных кривых и поверхностей из массива точек при помощи следующих команд: Сплайн по точкам, Сплайн по полюсам, Кривая Безье — на плоскости, Поверхность по сети точек, Поверхность по пласту точек, Поверхность по сети кривых — в пространстве.

Ограничения инструментов геометрических преобразований в CAD-системах

Как уже отмечалось в [10], CAD-системы, в принципе, имеют в своем составе всё необходимое для реализации построений. Отсутствие соответствующих инструментов может быть связано:

• с недостаточной распространенностью геометрических преобразований (кроме аффинной группы) среди специалистов-проектировщиков;
• с возможностью появления в результате преобразования несобственных (бесконечно удаленных) частей объекта, объектов с комплексными значениями параметров (мнимые фигуры) и т.п.;
• с недостаточной исследованностью многих геометрических преобразований (способы задания, что является результатом прямого и обратного преобразования для той или иной фигуры и др.).

Перечисленных недостатков лишены преобразования аффинной группы: хорошо изучены, не приводят к появлению несобственных и мнимых фигур. Именно они активно применяются в CAD-системах и вообще в геометрических и графических редакторах, библиотеках 3D-графики и др.

Поэтому к применению инструментов геометрических преобразований в CAD-системах представляется целесообразным ввести следующие ограничения:

• преобразования применяются к конечным объектам: отрезкам, дугам, окружностям, сегментам сплайнов, отсекам поверхностей, которые могут быть аппроксимированы некоторым числом точек, так что после преобразования получается столько же точек, которые затем соединяются известной кривой, поверхностью или сплайном;
• если в ходе преобразования некоторые точки становятся несобственными или мнимыми, это следует рассматривать как ошибку того же рода, что и Нарушение топологии, Система не имеет решений и др. Такая команда прерывается.

С учетом сказанного попробуем представить, как могут быть реализованы инструменты геометрических преобразований в CAD-системе типа КОМПАС-3D с учетом особенностей ее работы.

Подходы к реализации инструментов геометрических преобразований

Включение геометрических преобразований в качестве инструментов в состав CAD-систем может быть осуществлено следующими способами:

1 Плоское преобразование без параметризации. Так, к примеру, работают команды перенос/копирование, поворот, масштабирование и отражение в плоском режиме редактора. Проектировщик выбирает исходные фигуры, активирует команду, указывает объекты и/или вводит значения параметров преобразования. Преобразованные фигуры заменяют собой исходные или создаются как копии.

На рис. 3а показан пример зеркального отражения эллипса (показан красным) в момент щелчка левой кнопкой мыши на оси симметрии; на рис. 3б приведен «подобный» пример эквиформного преобразования Гирста (отражение относительно кривой) для образования кривой типа аэродинамического профиля ([4-6]).

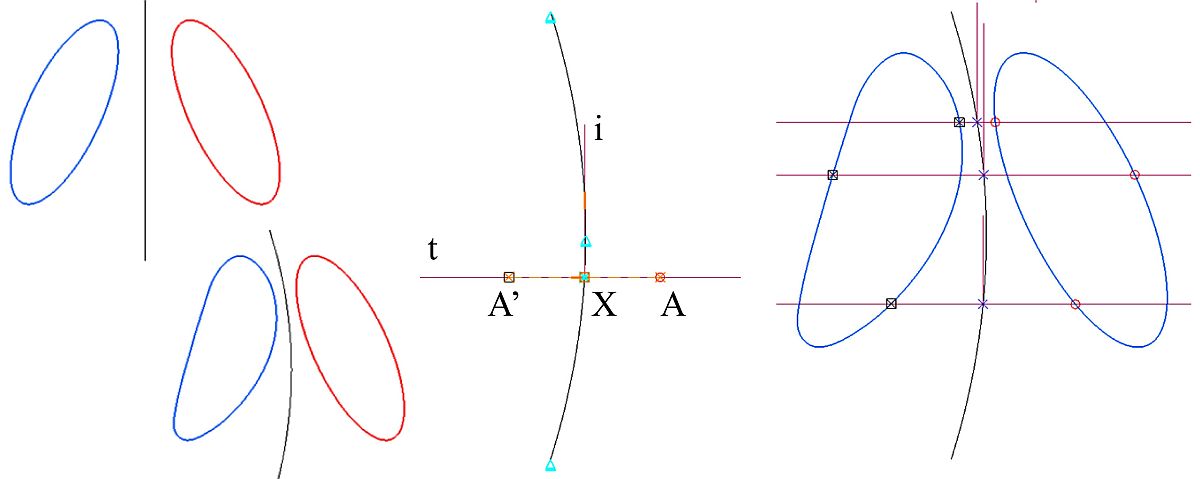
Рис. 3. Симметрия и нелинейная симметрия — преобразование Гирста

Такой подход может быть использован для небольшого числа преобразований, например самых известных: инверсии, гомологии, нелинейной симметрии, однако, как правило, проектировщик должен иметь возможность сам определять правила преобразования. В общем случае точка преобразуется в точку, линия — в линию, состоящую из преобразованных точек исходной кривой. Поэтому, фактически, достаточно описать в виде параметрической модели правило преобразования для одной точки и применить к точкам выбранной фигуры. Сделать это встроенные средства САПР КОМПАС-3D позволяют. На рис. 3в показана параметризованная модель: здесь зафиксирована кривая, относительно которой происходит отражение, точка А расположена произвольно, через нее построена горизонтальная прямая t, t пересекает кривую в точке Х, через X проходит вертикальная ось — отрезок i, относительно которого симметричны A и A’. Теперь если перемещать точку A по эллипсу (рис. 3г), то посредством параметрических связей точка A’ прочерчивает соответствующую кривую.

В настоящий момент применить такую параметризованную модель сразу к целой фигуре (эллипсу) невозможно, однако можно предположить команду, которая в качестве параметров будет получать параметризованное преобразование, например в виде макроэлемента, и одну или несколько фигур, к которым преобразование будет применено.

2 Плоское преобразование с параметризацией. В настоящее время в CAD-системах не реализуется. Присутствует в системе «Симплекс» [11, 12] и языке геометрических построений в работах [13, 14]. Требует сохранять фигуры-оригиналы. При любых изменениях фигур-оригиналов активируется преобразование и изменяются производные фигуры. Чтобы копии фигур до и после преобразования не создавали путаницы на экране в процессе работы, промежуточные экземпляры скрываются.

В настоящее время в САПР КОМПАС-3D имеется только один пример параметризации преобразований: в параметрическом режиме выполнение команды Зеркально отразить создает не только симметричные фигуры, но и параметрические связи, так что любые изменения исходных или производных фигур передаются через эти связи.

Описанный выше подход к созданию преобразованных фигур при помощи параметризованной модели внутри макроэлемента может быть использован и в этом случае: если сделать копии параметризованной модели и для каждой сдвинуть управляющую точку (А), мы получим множество преобразованных точек, которые будут параметрически связаны с исходными. Проведенный через них сплайн окажется параметрически связан с исходной кривой. В настоящее время такое копирование приходится выполнять вручную, а на практике может потребоваться несколько сотен и даже тысяч копий.

3 Пространственное преобразование. Так, к примеру, работают команды пространственного масштабирования или зеркального массива. Проектировщик активирует команду, указывает в видовом окне или дереве модели преобразуемые объекты, затем — вспомогательные объекты (например, плоскость отражения) и/или вводит значения параметров. В дерево модели добавляется элемент. Промежуточные объекты скрываются.

На рис. 4 показана модель элемента луковичного купола, состоящего из двух гладко сопряженных отсеков циклид Дюпена α и β, полученных инверсией конуса κ и цилиндра µ относительно сфер σ1 и σ2 соответственно [14].

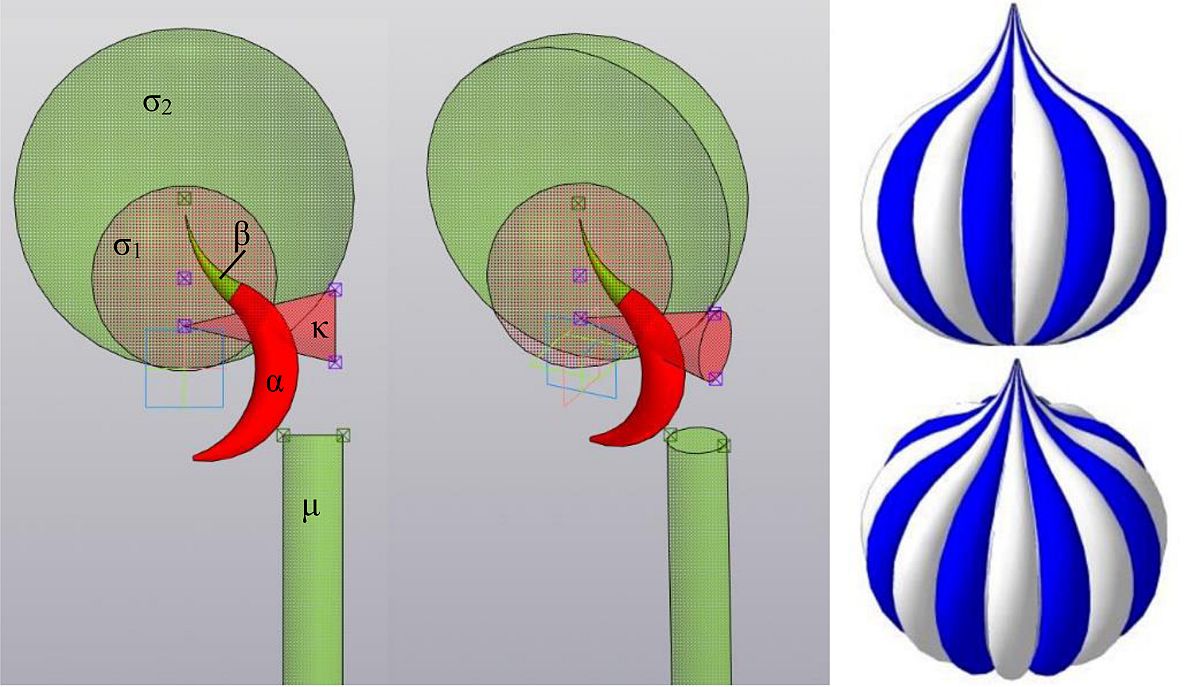
Рис. 4. Моделирование элемента купола при помощи инверсии:
а — исходные поверхности, сферы и циклиды; б — модель купола

Поскольку сфер среди стандартных фигур САПР КОМПАС-3D нет, преобразование инверсии проще всего задать центром и радиусом или некоторой точкой. Недостатки здесь, как и в п. 1: число возможных команд невелико. В общем случае требуется создание макроэлемента в дереве модели, который можно было бы применять к выбранным в модели точкам, кривым или отсекам поверхностей.

4 Пространственное расслаиваемое преобразование. В настоящее время в CAD-системах не реализуется. Расслаиваемые преобразования — это такие преобразования, которые можно выполнить, если ввести в трехмерное пространство пучок плоскостей и в каждой плоскости выполнить некоторое плоское преобразование части исходной фигуры. Например, пространственную симметрию относительно некоторой плоскости σ можно заменить на осевые симметрии в плоскостях, перпендикулярных σ. Говорят, что пространственная симметрия расслаивается на осевые симметрии в пучке плоскостей, перпендикулярных σ. Расслаиваемые преобразования удобны тем, что могут быть реализованы последовательным выполнением более простых (плоских) преобразований. Ближе всего к реализации этого типа преобразований в CAD-системах формообразующие операции (выдавливание, вращение, движение по траектории). Пусть имеется плоский контур, содержащий параметризованную модель преобразования, и пусть в процессе формообразования плоскость контура перемещается, контур перестраивается, так что пространственный элемент (тело или поверхность) создается не постоянным, а переменным контуром, форма которого зависит от положения его плоскости.

Для реализации параметрических связей такого движущегося контура с пространственной геометрией — прямыми, плоскостями, поверхностями и др. может быть полезным еще один механизм, в настоящее время явным образом отсутствующий в CAD-системах. На плоскость эскиза можно спроецировать пространственные точки и линии и добавлять затем параметрические связи. Другая геометрическая операция — сечение пространственных линий и поверхностей плоскостью эскиза — не реализуется. Сечение можно построить при помощи отдельной команды, а найденные точки и линии спроецировать, но для случая переменного контура это не подходит. Наоборот, возможность «зацепиться» за точки и линии сечения в эскизе позволила бы получить переменный контур и для каждого положения плоскости эскиза — свое плоское преобразование.

На рис. 5 показано образование каналовой поверхности µ с заданной площадью сечений как результат эквиформных преобразований эллипсов в сечении исходного эллиптического цилиндра α. В эскизе показаны a — эллипс в сечении цилиндра α, b — кривая в сечении поверхности β, относительно которой выполняется «отражение» эллипса, a’ — результат преобразования эллипса, C — требуемый центр сечения каналовой поверхности в сечении оси i плоскостью эскиза, a’’ — формообразующий контур, полученный сдвигом a’ в направлении центра.

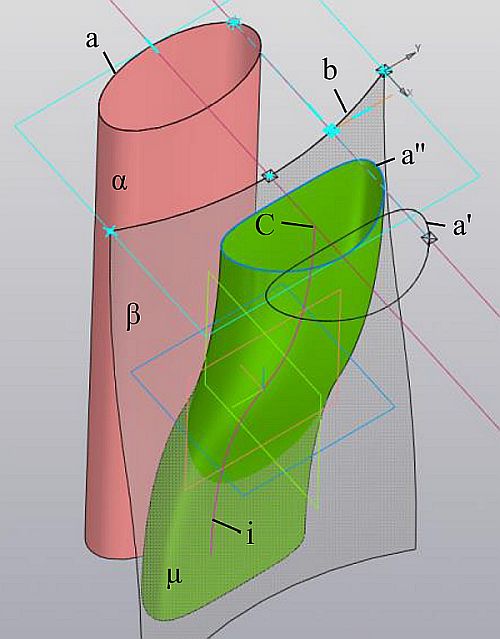
Рис. 5. Создание модели поверхности при помощи расслаиваемого преобразования

В системе КОМПАС-3D для операций Массив по… можно задать «Таблицу изменяемых переменных» и таким образом управлять экземплярами массива. Предлагаемый переменный контур обладает более широкими возможностями: параметры промежуточных сечений определяются автоматически на основе объектов модели, не требуется их вычислять и оформлять в виде таблицы, кроме того, автоматически создается тело или поверхность, как, например, при выполнении операций типа Элемент выдавливания (копий кривых при этом могло бы потребоваться несколько сотен или даже тысяч).

Заключение

Приведенные в работе примеры получены в ходе своеобразной симуляции преобразований в САПР КОМПАС-3D. Часть операций выполнялась вручную, при этом автор исходил из предположения, что в соответствующих инструментах подобные действия автоматизированы. Часть наиболее трудоемких — при помощи программ на языке геометрических построений из [13-15], а кривые и поверхности передавались в систему КОМПАС-3D как массивы координат точек.

Проведенный анализ показал:

• преобразования являются мощным инструментом конструирования;
• в CAD-системах, в частности САПР КОМПАС-3D, широкий набор геометрических преобразований может быть реализован путем модификации имеющихся средств и инструментов.

Представленные в настоящей статье соображения были переданы разработчикам САПР КОМПАС-3D. Это позволяет надеяться, что между отечественными разработчиками САПР и специалистами в области конструктивного геометрического моделирования завяжется продуктивный диалог, а развитие отечественных систем компьютерной геометрии пойдет не только по пути копирования западных продуктов, но и создания систем с новыми уникальными и практически полезными возможностями.

Литература:

1. Рузинов Л.Д. Проектирование и расчет механизмов на основе геометрических преобразований. М.-Л.: Машиностроение, 1964. 148 с.
2. Бергер Э.Г., Переяслова С.М., Табацков В.П. К синтезу направляющих центроидных механизмов методом инверсии // Прикладная геометрия и инженерная графика. Киев: Будівельник, 1987. Вып. 43. С. 87-88.
3. Бергер Э.Г., Коренчук А.Ю. Геометрическое конструирование механизмов автоматических манипуляторов на основе B-преобразования // Прикладная геометрия и инженерная графика. Киев: Будiвельник, 1991. Вып. 51. С. 89-91.
4. Боровиков И.Ф., Иванов Г.С., Суркова Н.Г. О применении преобразований при решении задач начертательной геометрии // Геометрия и графика. 2018. № 2. С. 78-84. DOI: 10.12737/article_5b55a35d683a33.30813949.
5. Искакова С.Д. Об использовании нелинейной симметрии в описании аэродинамических профилей // Начертательная геометрия и черчение. Алма-Ата, 1981. С. 19-22.
6. Иванов Г.С. Конструирование технических поверхностей (математическое моделирование на основе нелинейных преобразований). М.: Машиностроение, 1987. 192 с.
7. Михайленко В.Е., Ковалев С.Н. Конструирование форм современных архитектурных сооружений. Киев: Будiвельник, 1978. 112 с.
8. Ковтун В.П. Проектирование судовой поверхности методом топологических преобразований // Прикладная геометрия и инженерная графика. Киев: Будiвельник, 1965. Вып. 1. С. 162-168.
9. Кокарева Я.А. Конструирование каналовых поверхностей с переменной образующей и плоскостью параллелизма на основе эквиаффинных преобразований плоскости // Геометрия и графика. 2017. № 1. С. 12-20. DOI: 10.12737/25119.
10. Бойков А.А. Некоторые вопросы автоматизации конструктивных алгоритмов формирования геометрических моделей для CAD-систем // SCVRT’2018. Труды Международной науч. конф. МФТИ (ГУ) ИФТИ. Москва-Протвино, 2018. С. 281-290.
11. Волошинов Д.В. О перспективах развития геометрии и ее инструментария // Геометрия и графика. 2014. № 1. С. 15-21. DOI: 10.12737/3844.
12. Волошинов Д.В. Конструктивное геометрическое моделирование. Saarbrucken: Lambert Academic Publishing, 2010. 355 с.
13. Boykov A.A. Development and application of the geometry constructions language to building computer geometric models // Journal of Physics: Conference Series. 2021. Volume 1901 (012058). С. 1-8. DOI: 10.1088/1742-6596/1901/1/012058.
14. Boykov A.A. Modeling of geometric correspondences and transformations via geometry constructions language // Journal of Physics: Conference Series. 2022. Volume 2182 (012001). С. 1-9. DOI: 10.1088/1742-6596/2182/1/012001.
15. Бойков А.А. Язык геометрических построений и его применение в разработке функций CAD-систем // SCVRT’2019. Труды Международной науч. конф. МФТИ (ГУ) ИФТИ. Нижний Новгород, 2019. С. 42-50.