На прошедшем 31 мая форуме компании «Топ Системы» одна из основных сессий была посвящена представлению продукта компании «Топ Системы» — геометрического ядра RGK. Сессию вели директор по разработке компании Сергей Козлов и заместитель директора по развитию технологий 3D-моделирования Леонид Баранов. Он, в частности, является руководителем группы разработки геометрического ядра RGK.

В первой части секции Сергей Козлов рассказал об истории создания и текущем статусе геометрического ядра.

Разработка геометрического ядра RGK, по сути, началась в далеком 1984 году, когда в Московском станкоинструментальном институте (позже МГТУ «Станкин») была организована группа по исследованиям в области геометрического моделирования и разработке 3D-ядра под руководством доцентов А.В. Рыбакова и В.Ю. Судзиловского. Именно с того момента Леонид Баранов начал заниматься этой работой в качестве математика-программиста, а позже, после завершения учебы в Станкине, возглавил эту группу. Результат работы оказался существенным. В 1995 году была выпущена версия T-FLEX CAD, в которой функциональность 3D-моделирования обеспечивалась собственным геометрическим ядром. Ресурсов для ведения столь наукоемкой и дорогостоящей разработки у компании на тот момент было недостаточно. Одновременно с этим представилась возможность лицензировать геометрическое ядро ACIS, а потом и Parasolid. Так, в 1996 году была выпущена 6-я версия T-FLEX CAD на геометрическом ядре ACIS, а в 1998-м вышла версия 7 на ядре Parasolid. Таким образом, разработчики T-FLEX CAD получили возможность поработать со всеми основными геометрическими ядрами и оценить их архитектуру и особенности.

В 2011 году МГТУ «Станкин» получил контракт на разработку российского геометрического ядра в рамках развития программы отечественного станкостроения. В качестве задела этой работы были взяты наработки компании «Топ Системы». С целью обеспечения наиболее современного уровня решения алгоритмы ядра были практически полностью модернизированы, но основные подходы к реализации сохранены. По завершении работы по контракту в 2013 году компания «Топ Системы» не остановила разработку RGK (именно в то время получил название этот продукт), а продолжила его развитие.

Геометрическое ядро RGK нашло свое применение в проекте «Гербарий», который компания «Топ Системы» выполняла по заказу Фонда перспективных исследований (ФПИ) в 2015-2016 годах, а также в проекте СПЖЦ «Цифровое предприятие» («САРУС») — проекте, первый этап которого завершился совсем недавно. В разработке этого проекта компания «Топ Системы» приняла самое активное участие.

В настоящее время компания «Топ Системы» получила все возможности по самостоятельному развитию и выводу на рынок RGK в качестве коммерческого продукта. Продукт будет поставляться сразу для нескольких платформ, включая различные версии Linux, в том числе отечественные сертифицированные версии. Поставка продукта планируется в виде библиотеки классов для использования на языке программирования C++, а также всех компонентов, необходимых для удобного применения в конечных системах. Комплект инструментов разработчика (SDK) включает в себя:

• исполняемые модули;
• библиотечные и заголовочные файлы, необходимые для сборки конечного приложения;
• файл электронного руководства в виде гипертекстовой справки;
• набор примеров в исходных кодах;
• исполняемую программу RGKWorkshop — тестовую и отладочную оболочку, являющуюся одновременно и средством анализа, и средством отладки геометрических моделей;
• описание формата хранения моделей RGK — RGK_XML.

Особо стоит отметить, что формат хранения данных RGK_XML является открытым и специфицированным. Он имеет понятную структуру, соответствующую общим принципам организации модели данных RGK. Формат может быть использован с целью стандартизации для обеспечения представления точной геометрической модели данных объектов.

Вторую часть секции вел Леонид Баранов. Он рассказал о принципах построения модели данных геометрического ядра RGK, его архитектурных особенностях и наиболее сложных и интересных задачах, которые приходится решать разработчикам модуля. Рассказ сопровождался большим количеством иллюстраций и демонстрацией сравнительных тестов.

Геометрическое ядро RGK обеспечивает моделирование геометрических объектов по классической схеме граничного представления (B-Rep) с «точной» геометрией — с использованием аналитического представления кривых и поверхностей разных типов. Такое представление позволяет моделировать объекты с высокой точностью, одновременно обеспечивая возможность работы с толерантной геометрией, когда вместе с объектами модели хранится точность, с которой они были рассчитаны. Параметры точности толерантной геометрии применяются при всех вычислениях, выполняемых в коде ядра. Данная особенность обеспечивает возможности по сохранению целостности геометрической модели даже для очень сложных геометрических форм и невысокой точности исходных данных.

Геометрическое ядро обеспечивает выполнение следующих основных функций:

• хранение геометрической модели (геометрии/топологии тел, поверхностей, кривых);
• создание и редактирование геометрической модели;
• управление идентификацией и атрибутами геометрической модели;
• контроль целостности и качества геометрической модели;
• измерение и анализ геометрической модели;
• построение плоскогранных представлений (тесселяции) модели с целью визуализации или подготовки данных для генерации расчетных (CAE) сеток;
• генерация проекций и видов.

Классы геометрического ядра RGK, доступные для использования в конечных приложениях, обеспечивают как низкоуровневую функциональность для создания и редактирования геометрии, так и высокоуровневые специализированные функции, которые в ядре называются генераторами. Так, в составе библиотеки классов ядра имеются следующие генераторы:

• примитивы (призма, тор, сфера, цилиндр, конус);
• кинематические операции (вытягивание, вращение, по траектории, по сечениям);
• булевы операции (глобальные, локальные, селективные);
• операции сглаживания различных типов (фаски, реберное сглаживание, трехгранное сглаживание, сглаживание граней);
• операция оболочки/тела смещения/придания толщины;
• операция уклона граней;
• операции удаления/замены/трансформации граней (так называемые операции прямого моделирования);
• операции сшивки/разрезания;
• операции копирования/трансформации тел, в том числе с использованием различных масштабов по осям;
• ряд низкоуровневых операций с телами, а также множество операций с кривыми.

Функциональность многих генераторов в RGK весьма развитая. Остановимся на описании особенностей некоторых из операций, поддерживаемых ядром.

Например, в генераторе «по траектории» и «по сечениям» поддерживается ряд довольно продвинутых опций. Возможно задание законов кручения и масштабирования протягиваемого контура как отдельно, так и в комбинации (рис. 1), а также задание нескольких траекторий и различных способов их синхронизации. Кроме того, поддерживается обработка изломов на траектории движения (рис. 2 и 3).

Рис. 1. Протягивание по траектории с масштабированием и/или кручением

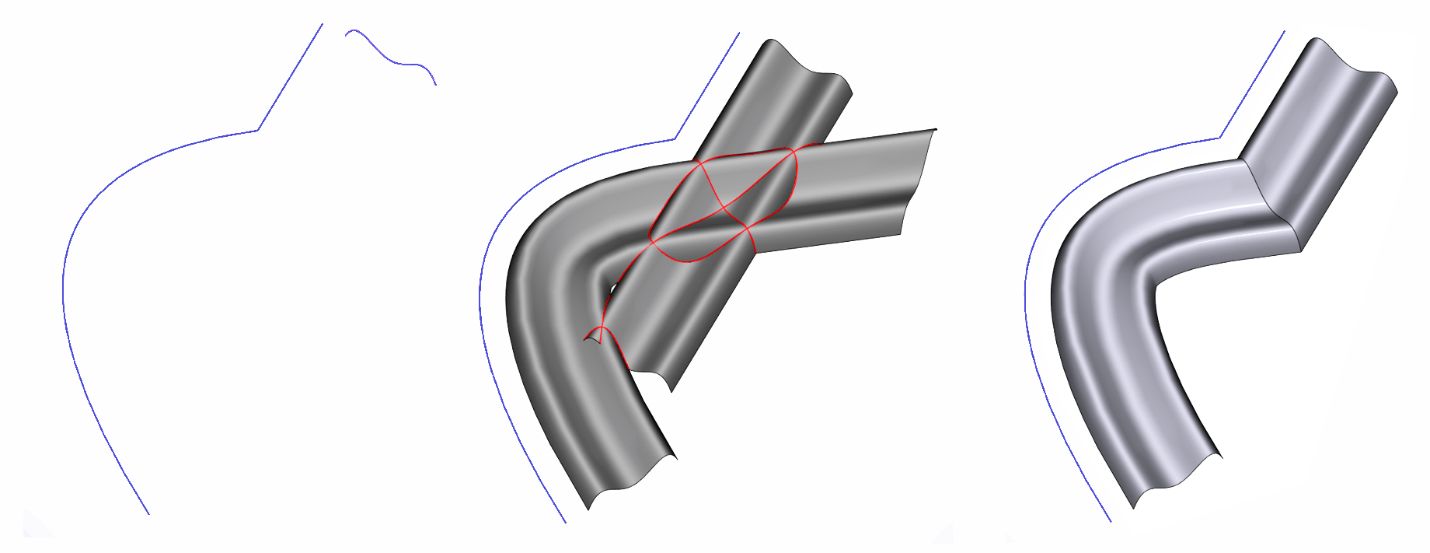
Рис. 2. Обработка изломов при протягивании по траектории

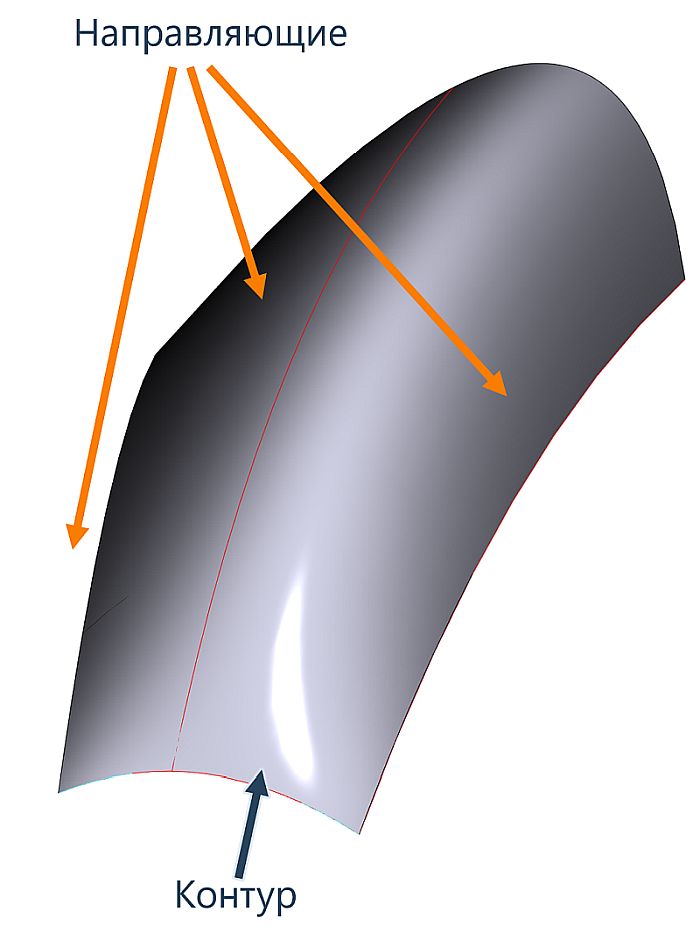
Рис. 3. Протягивание по траектории по трем направляющим

При построении поверхностей в ядре особое внимание уделяется их качеству — как с точки зрения соблюдения требований точности построения, так и в плане минимизации количества управляющих точек и регуляризации параметризации. Поскольку разработчики RGK имеют прямой доступ к функциональности, пожалуй, лучшего твердотельного ядра в мире — Parasolid, это позволяет проводить непредвзятые исследования и сравнение результатов. В настоящее время качество алгоритмов генерации поверхностей в RGK в целом сопоставимо с этим ядром и продолжает постоянно совершенствоваться, так как текущей задачей разработчиков является достижение функционального паритета с лучшими мировыми ядрами. В связи с этим в процессе разработки проводится большая исследовательская работа по анализу качества алгоритмов по сравнению с другими конкурирующими решениями «тяжелого» класса.

Как известно, одним из наиболее сложных как в математическом, так и алгоритмическом отношении классом задач геометрического моделирования являются задачи сглаживания (скругления) поверхностей. Учитывая это, при разработке ядра RGK особое внимание уделяется именно данной функциональности. В настоящее время в сглаживании ребер поддерживаются практически все основные режимы управления формой, известные по функциональности так называемых систем «тяжелого» класса: сечение постоянного и переменного радиуса; заданная ширина как в постоянном, так и переменном режимах; переменные сечения с кривыми второго порядка (эллипсы, параболы, гиперболы); режимы гладких переходов и сохранения ребер на всех типах сглаживаний; сохранение кривизны — G2-гладкость (рис. 4); задание отступов от вершины при вершинном сглаживании. Особенно стоит отметить архитектуру алгоритма, которая позволяет в едином формализме поддерживать сглаживание как ребер, так и граней и трехгранное сглаживание, тем самым обеспечивая очень высокую гибкость алгоритма и возможность развития. Большая работа проделана в части топологической робастности алгоритма сглаживания. Например, в зависимости от заданного радиуса алгоритм умеет делать большие перестройки топологии тела (рис. 5 и 6).

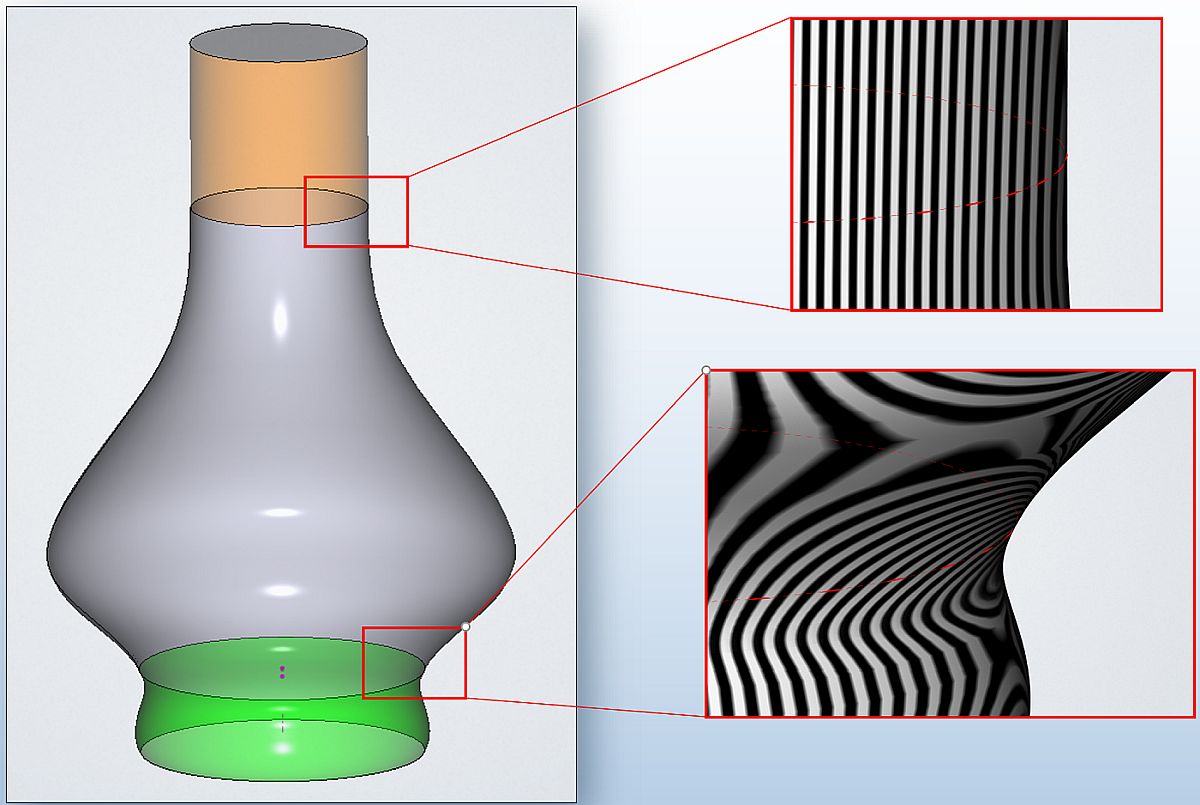
Рис. 4. Задание граничных условий в генераторе «по сечениям»:
G2-гладкое сопряжение поверхностей

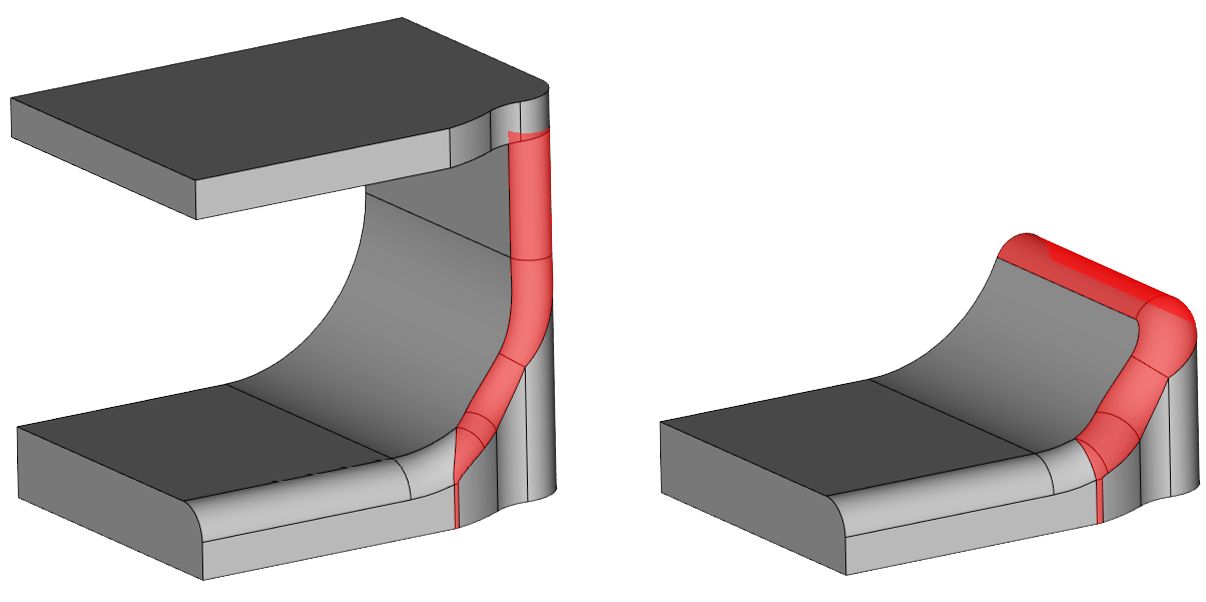
Рис. 5. Алгоритм «не цепляется» за родительские ребра — его поведение определяется радиусом

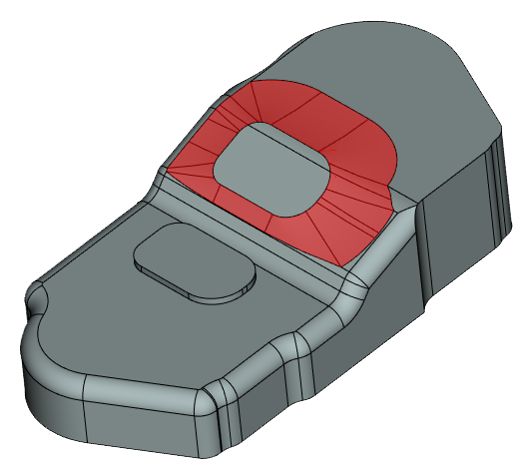
Рис. 6. Выход алгоритма сглаживания на соседние грани при большом радиусе поверхности (режим сохранения ребра)

Является допустимым построение сглаживания большего радиуса по меньшему. Такая задача возникает довольно часто при практическом моделировании (рис. 7).

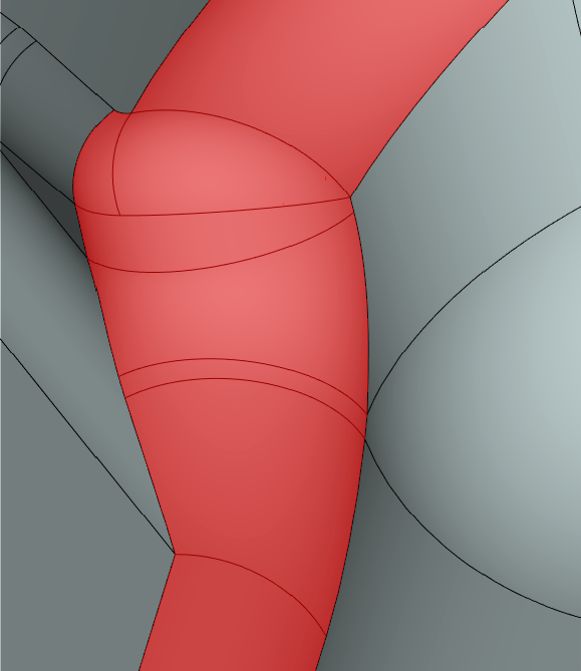
Рис. 7. Обработка участков с радиусом кривизны меньшим, чем текущий радиус сглаживания

Поддерживаются различные «переполнения», то есть переходы на гладкие соседние грани, а также, при необходимости, сохранение ребер (рис. 8-10).

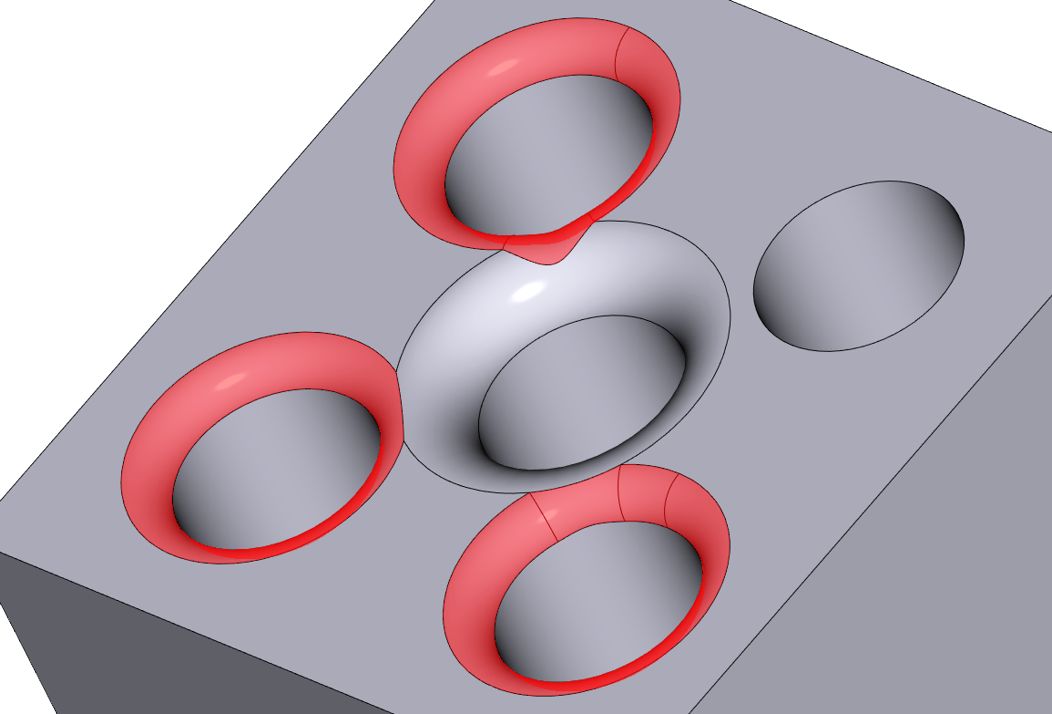
Рис. 8. Поддержка различных сценариев при выходе на гладкие ребра

 

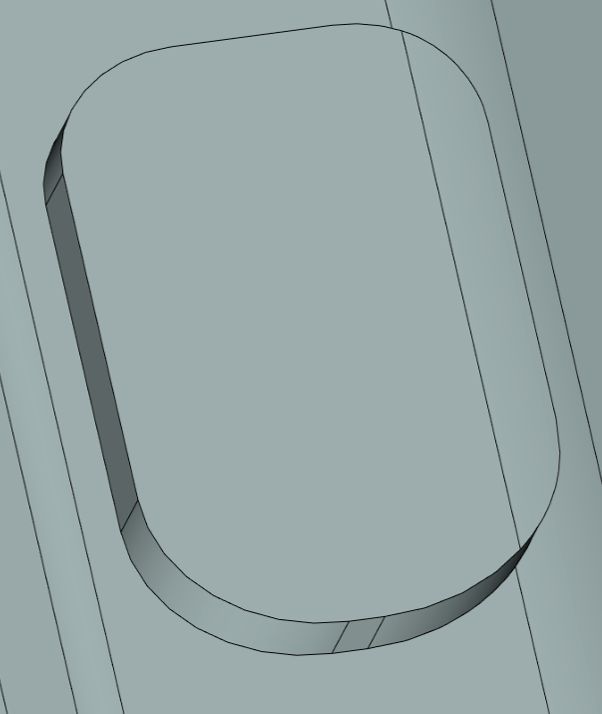
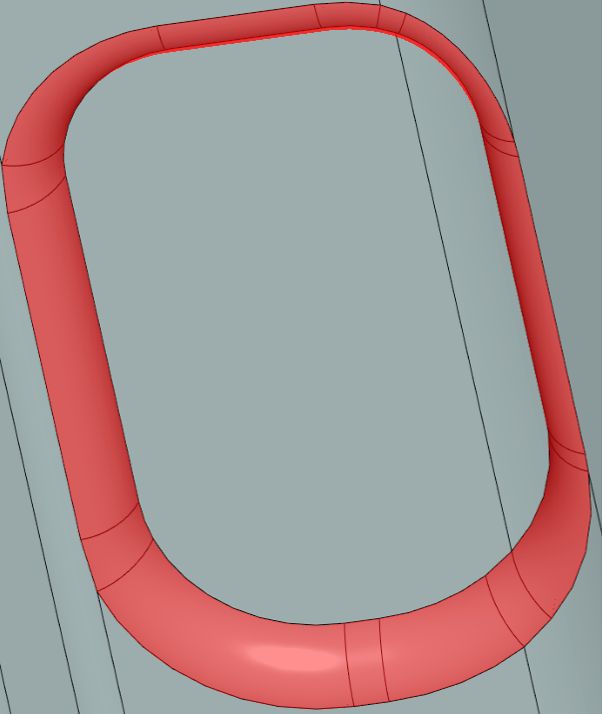
Рис. 9. Сохранение ребра при работе с большими радиусами сглаживания

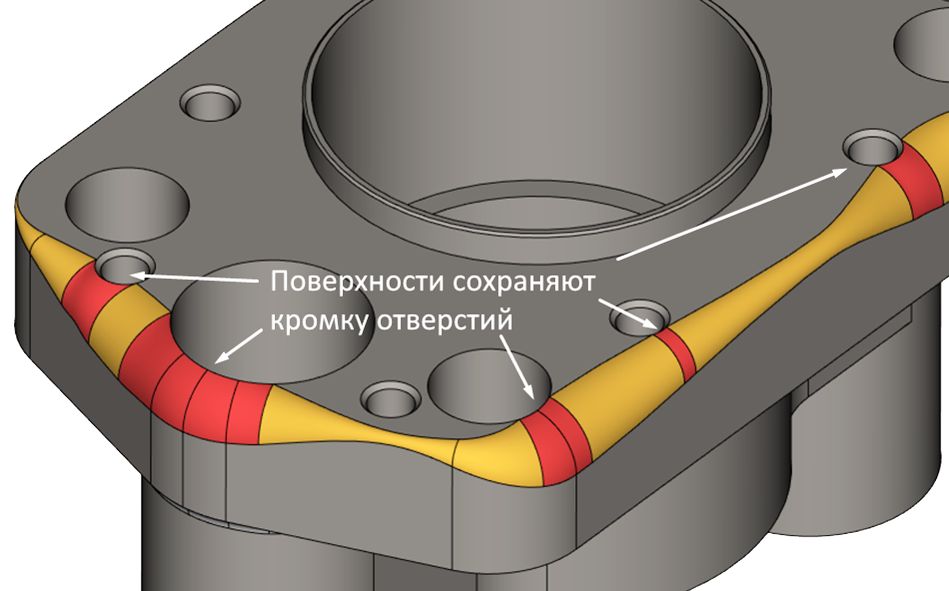
Рис. 10. Режим сохранения острых ребер на переменном сглаживании (обеспечивается
G1-гладкость всей последовательности граней)

Особого внимания заслуживает способность алгоритма сглаживания RGK обрабатывать вырождение топологических элементов (рис. 11).

 

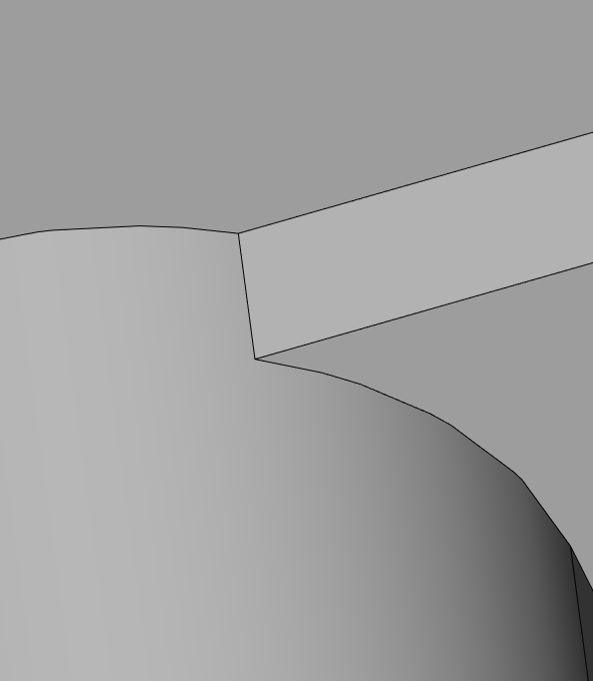
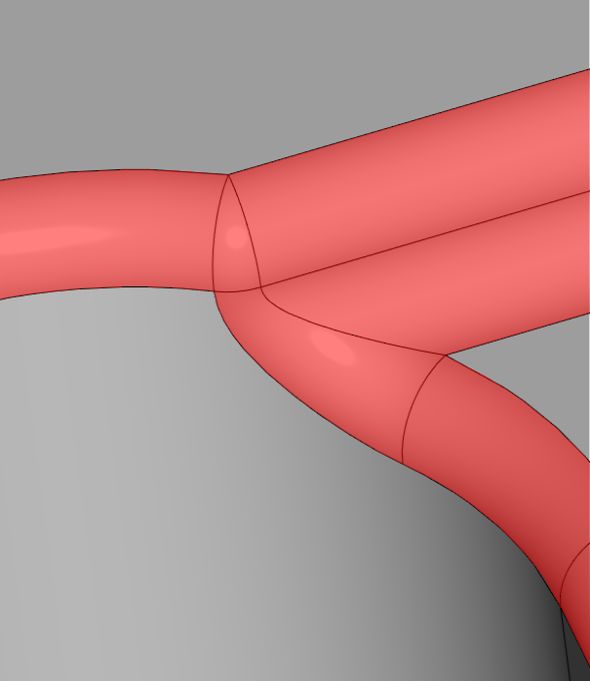
Рис. 11. Обработка исчезновения граней в предельном случае

Поддерживается сложная топология перекрытий сглаживаний, что значительно повышает качество работы алгоритма при реальном применении (рис. 12).

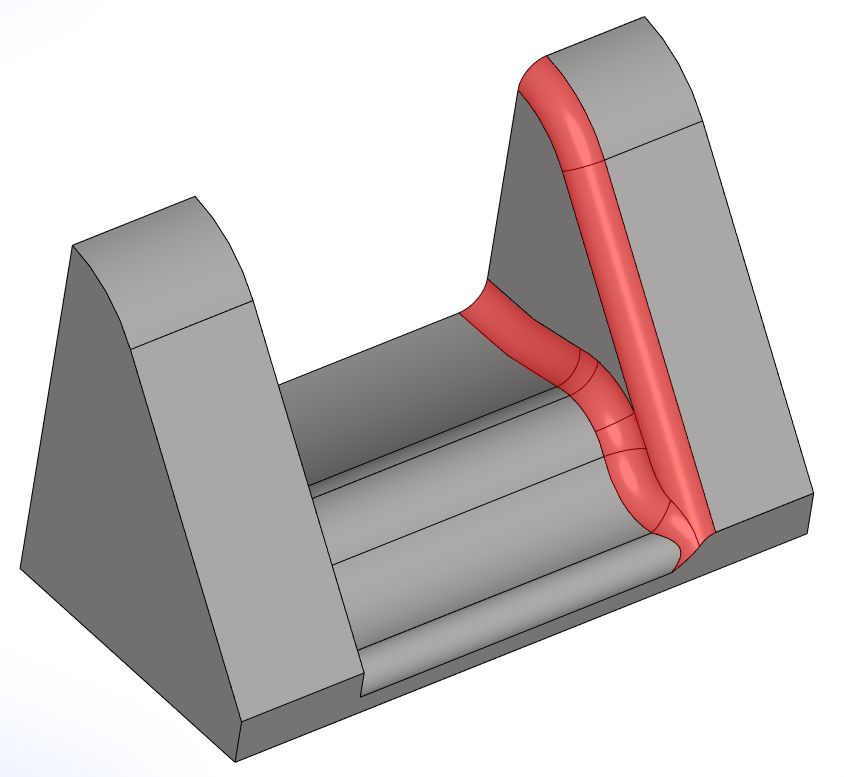
Рис. 12. Пример поддержки перекрытия сглаживаний из нескольких граней

Интересные результаты достигнуты при построении переменного сглаживания. В частности, поддерживается обработка перекрытия сглаживающих последовательностей с перевычислением закона изменения радиуса в области перекрытия (рис. 13).

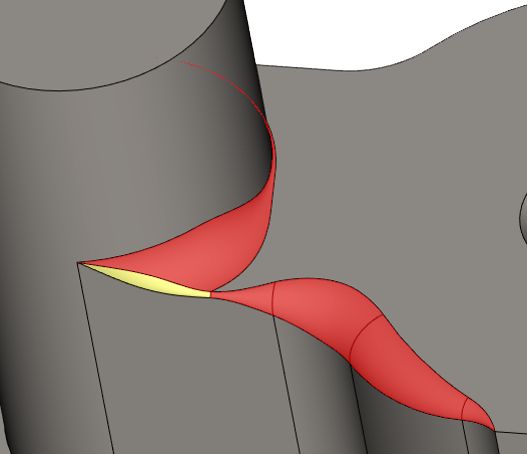
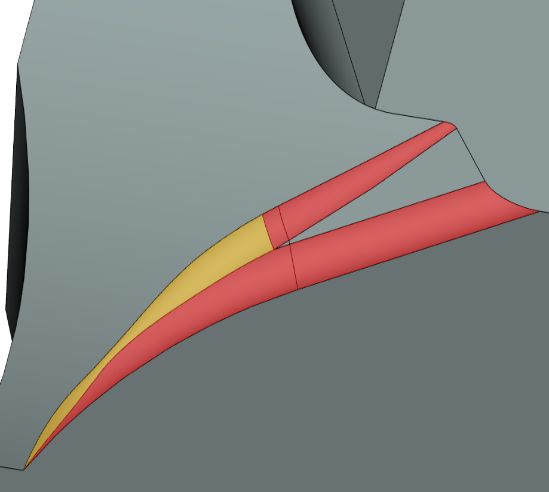
Рис. 13. Выпукло-вогнутое сглаживание переменным радиусом

Естественно, алгоритмами RGK реализована поддержка различных сечений переменного радиуса (рис. 14-18).

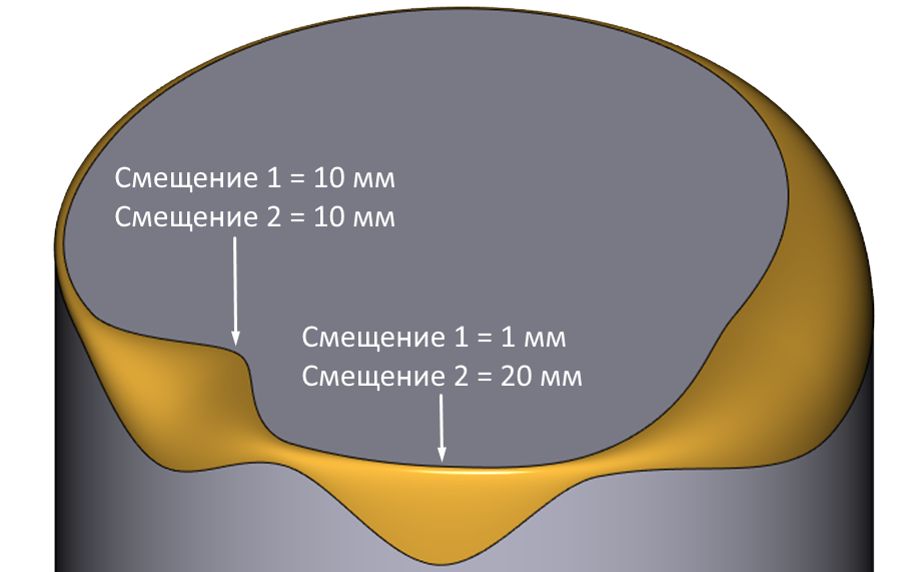
Рис. 14. Использование переменных законов смещения при реберном сглаживании в RGK

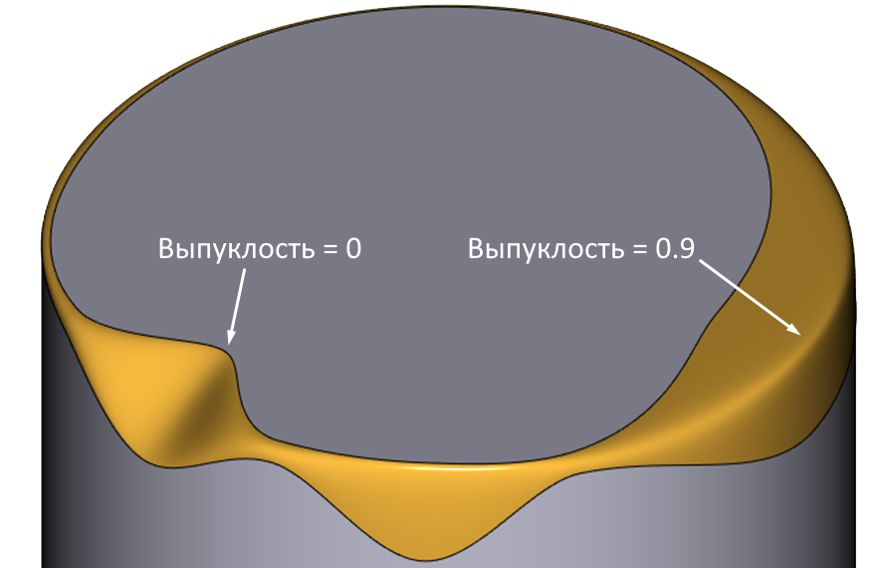
Рис. 15. Использование управления типом кривой сечения через выпуклость-дискриминант конического сечения (переход от отрезка прямой к гиперболе)

Рис. 16. Поддержка G2-гладкости на переменном и постоянном радиусах

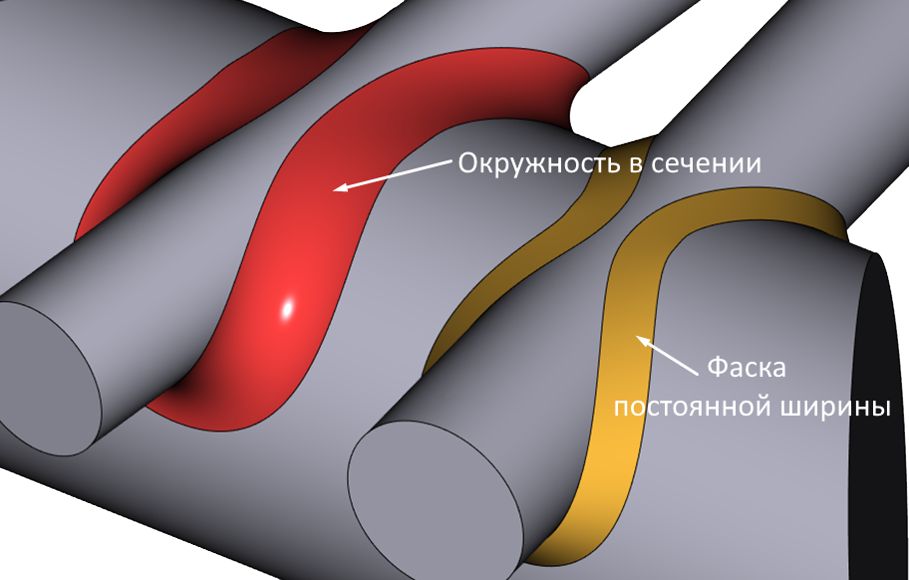
Рис. 17. Поддержка режима постоянной ширины сечения для разных типов сечения

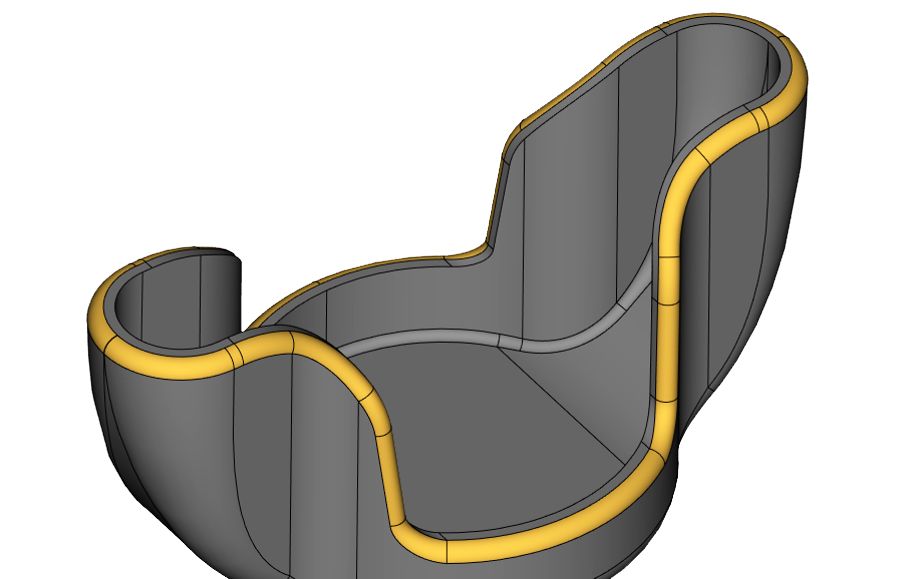
Рис. 18. Пример работы режима заданной ширины

Кроме того, разработана математика построения гладких «затягиваний» n-угольных областей (рис. 19).

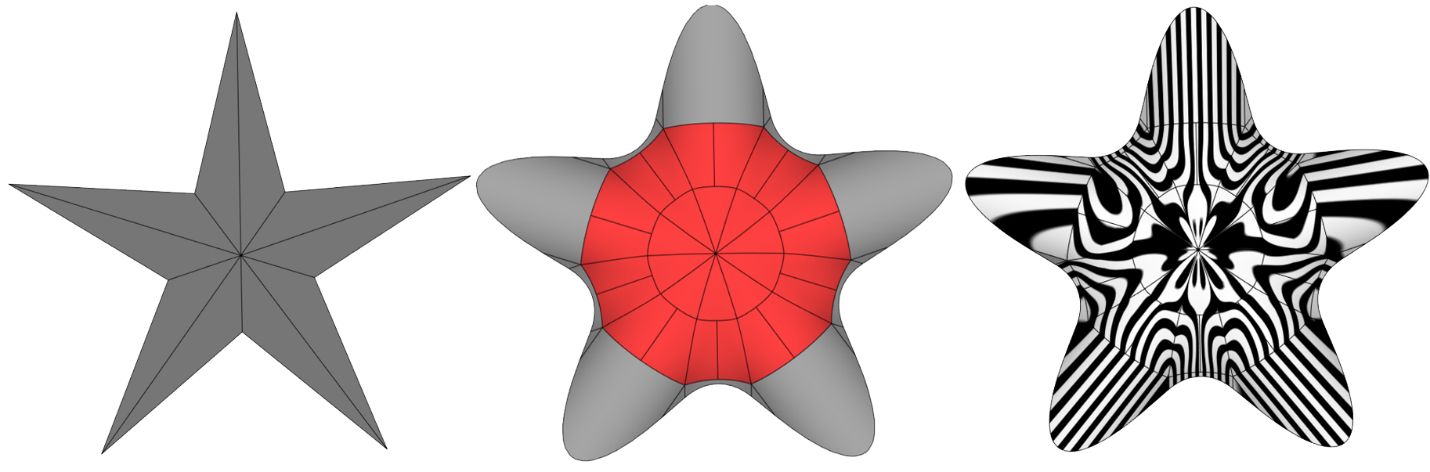
Рис. 19. G1-затягивание n-угольных областей

Эти разработки позволяют, в частности, решать задачу построения поверхностей с отступами от вершины (setback) — рис. 20 и 21.

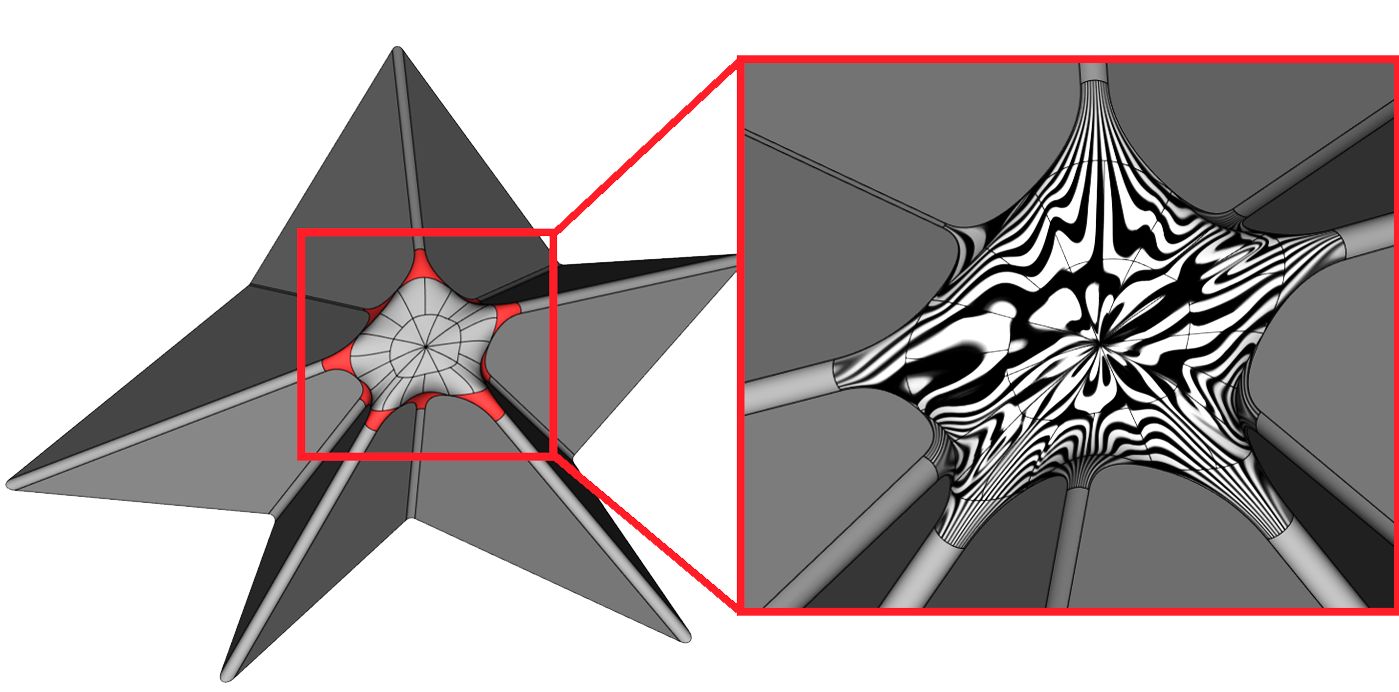
Рис. 20. Применение алгоритма затягивания области для задачи отступов

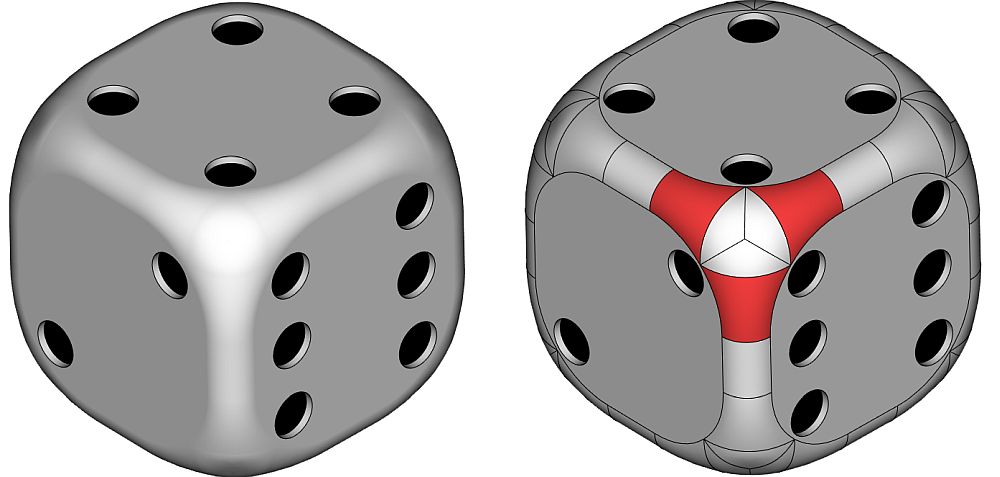
Рис. 21. Наглядный пример задачи отступов

Алгоритм сглаживания работает как на твердых, так и на поверхностных телах — в RGK нет различий между этими топологиями (рис. 22).

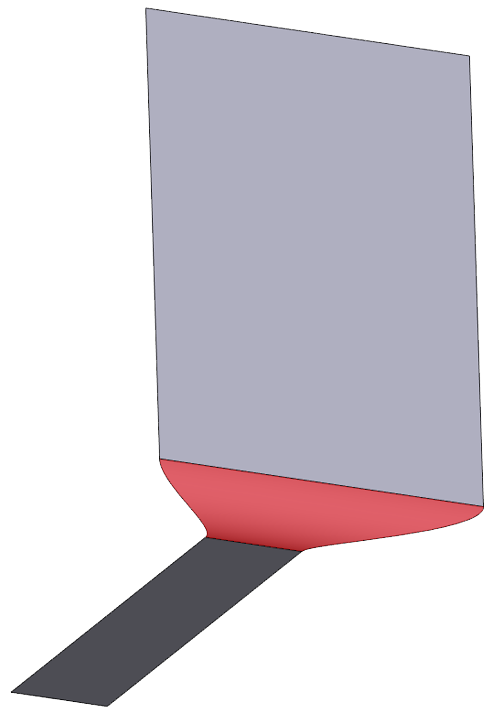
Рис. 22. Сглаживание ребра поверхностного тела

В ядре RGK функциональность сглаживания граней реализована, по сути, тем же самым алгоритмом, что и сглаживание ребер, — отличие только в интерфейсе верхнего уровня, но при этом решаются классические задачи сглаживания граней (рис. 23-25).

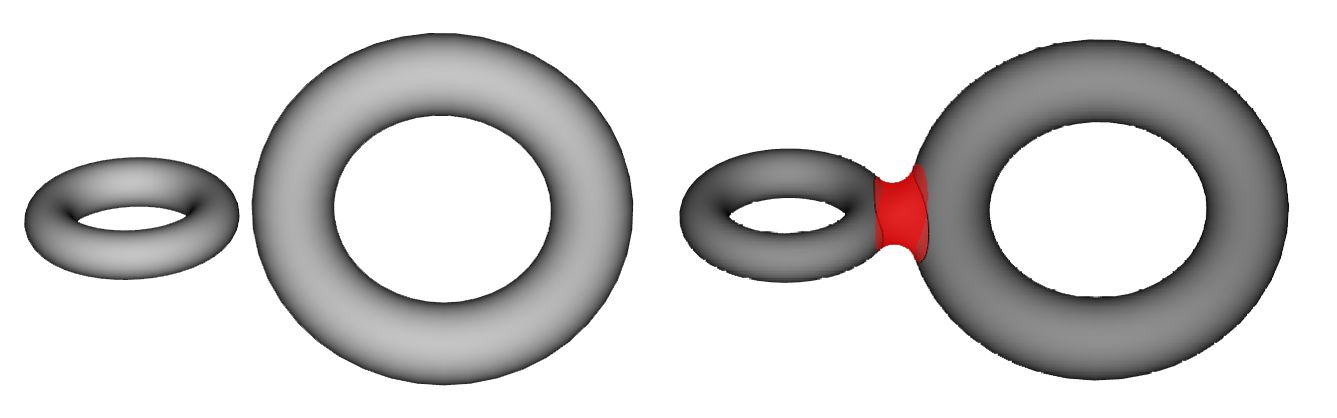
Рис. 23. Сглаживание граней, принадлежащих разным телам

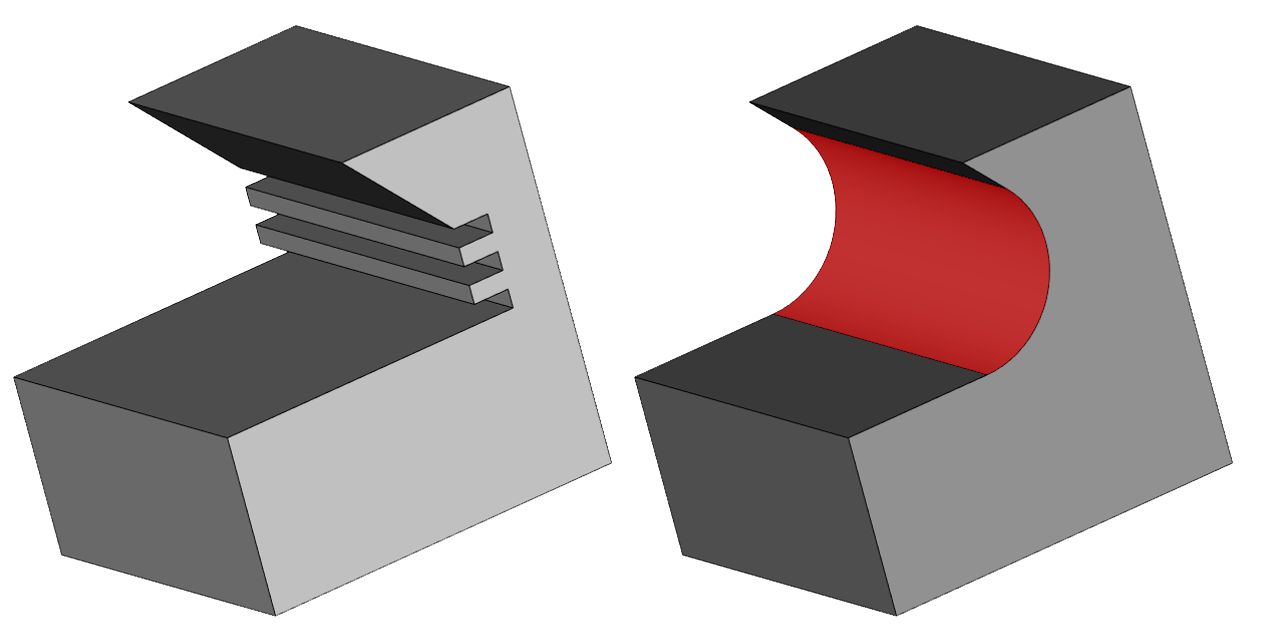
Рис. 24. Сглаживания граней с удалением сложной топологии

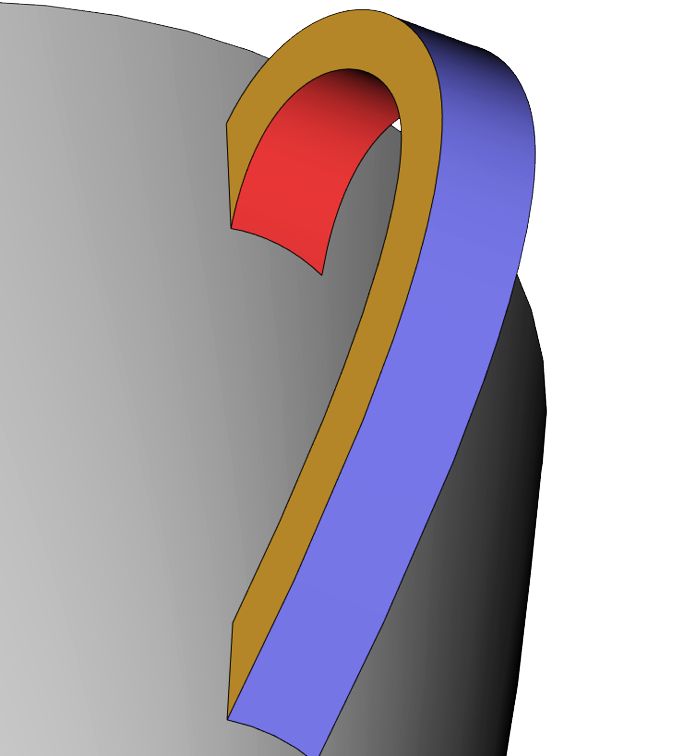
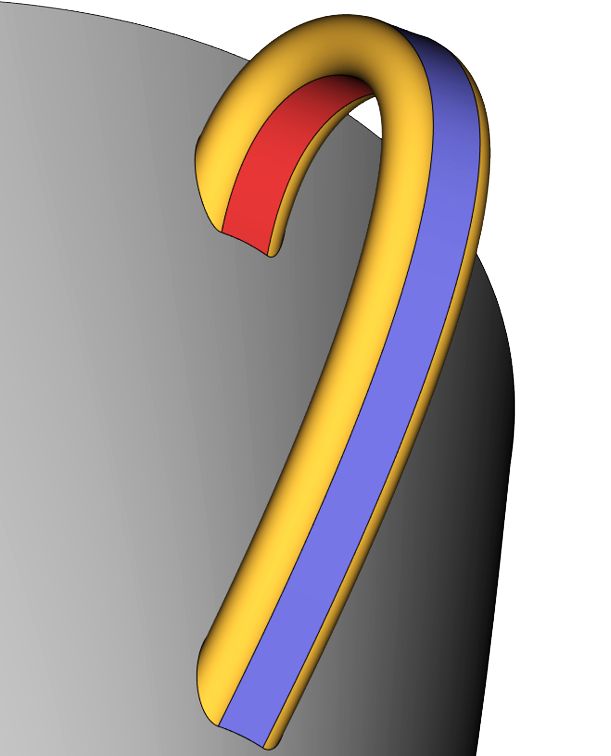
Рис. 25. Пример трехгранного сглаживания — поверхность, касательная к трем стенкам

Так как ядро RGK изначально разрабатывается с целью конкуренции с лучшими мировыми промышленными ядрами, в число инструментов ядра внесена различная функциональность, которая требуется прикладным системам «тяжелого» класса для решения различных специальных задач. Например, задача построения уклона граней формулировалась изначально как задача с указанием фиксированных ребер произвольной геометрии и возможностью изменения топологии тела в процессе операции (рис. 26).

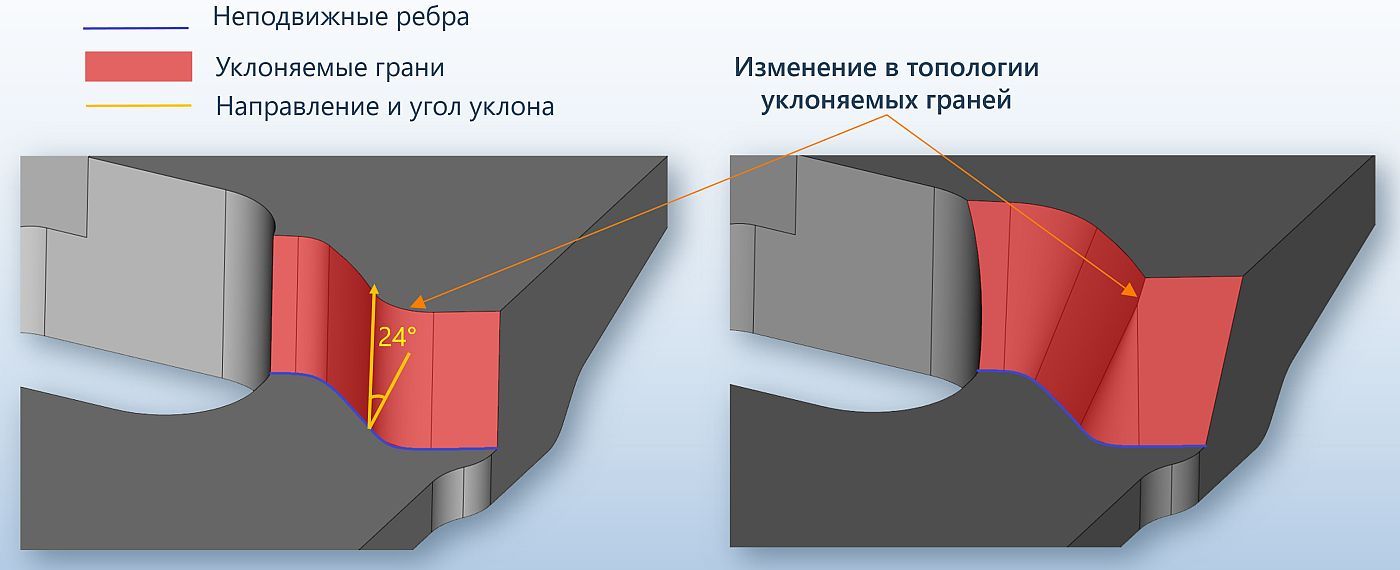
Рис. 26. Построение уклона граней с фиксированным ребром и изменением топологии модели

Уклон относительно поверхности разъема, конечно, тоже поддерживается, как частный случай более общей постановки (рис. 27).

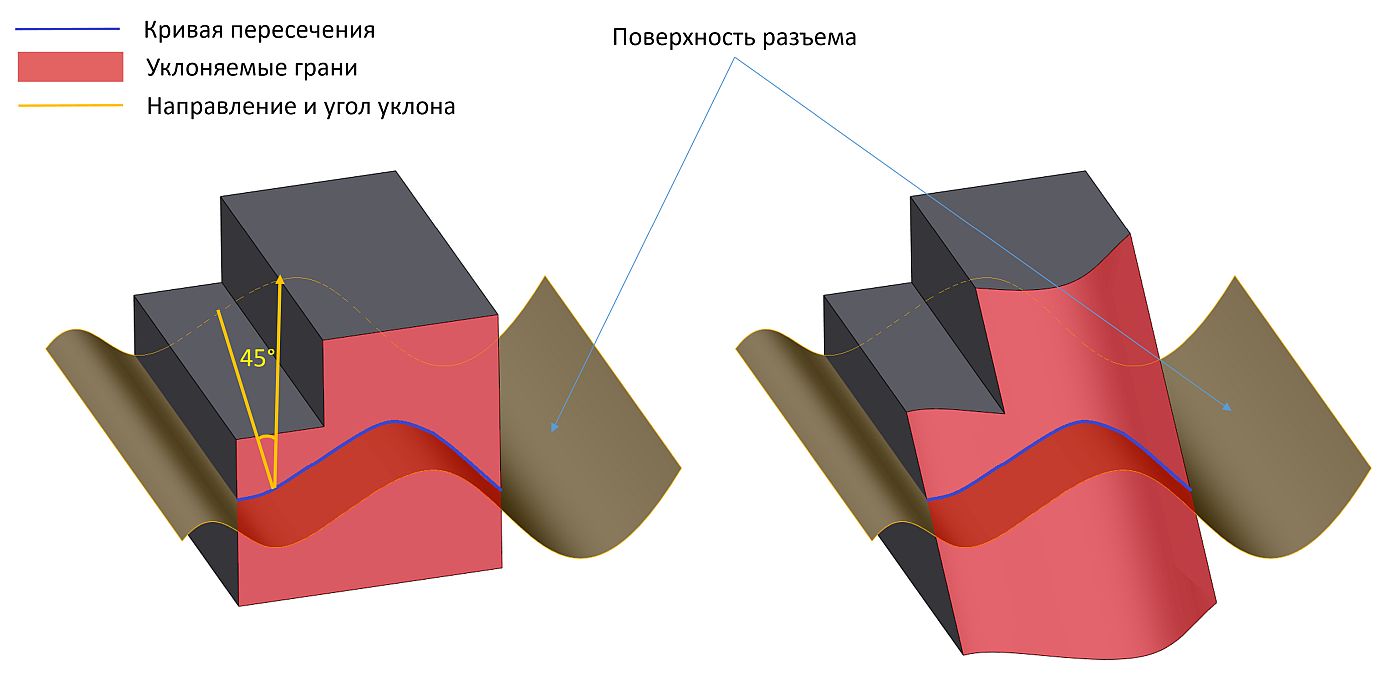
Рис. 27. Построение уклона грани с заданной поверхностью разъема

Другой пример: в булевых операциях помимо традиционного «глобального» режима операций (объединение, вычитание и пересечение) предусмотрены режимы локальных операций, когда приложение может указать, с какими именно гранями надо проделывать селективные булевы операции с возможностью выбора частей исходных тел, которые останутся в результате. Кроме того, предусмотрена обобщенная булева операция, которая может формировать топологическую модель, представляющую тела, контактирующие друг с другом по граням и ребрам. Важно также отметить, что булевы операции работают как над твердыми, так и над поверхностными телами, а также их комбинациями (рис. 28-32).

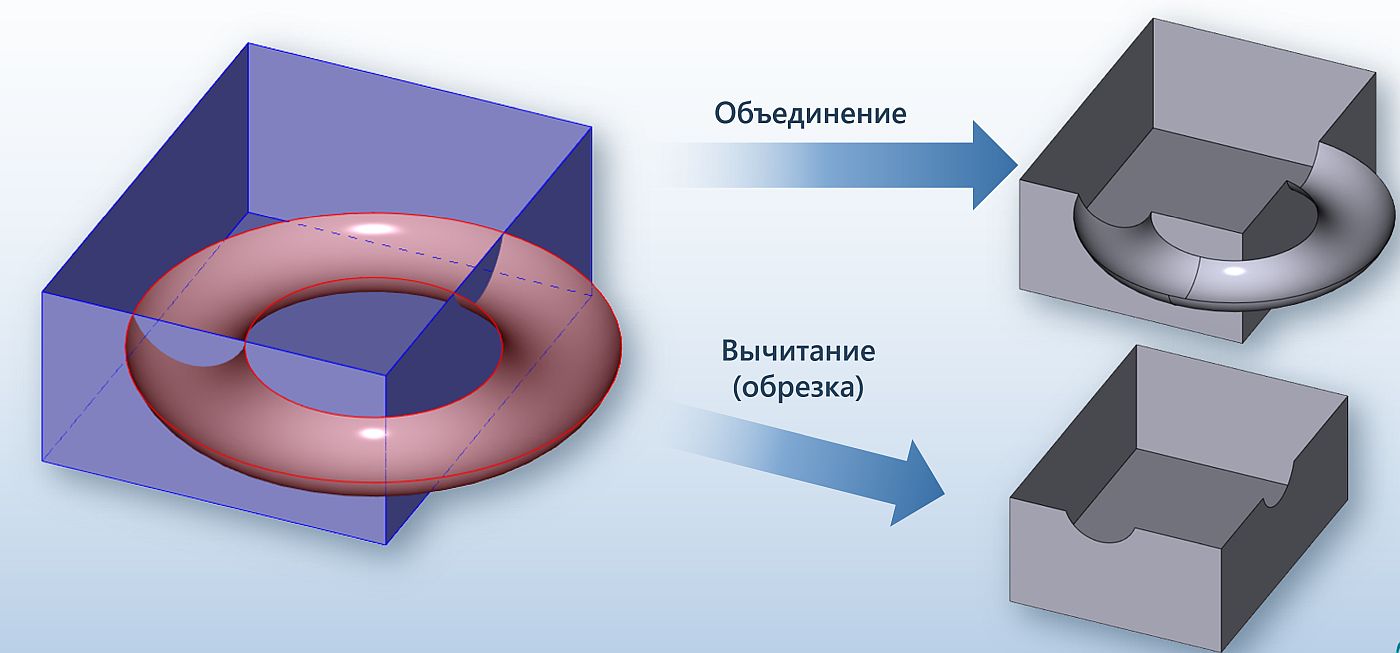
Рис. 28. Булевы операции над поверхностными телами

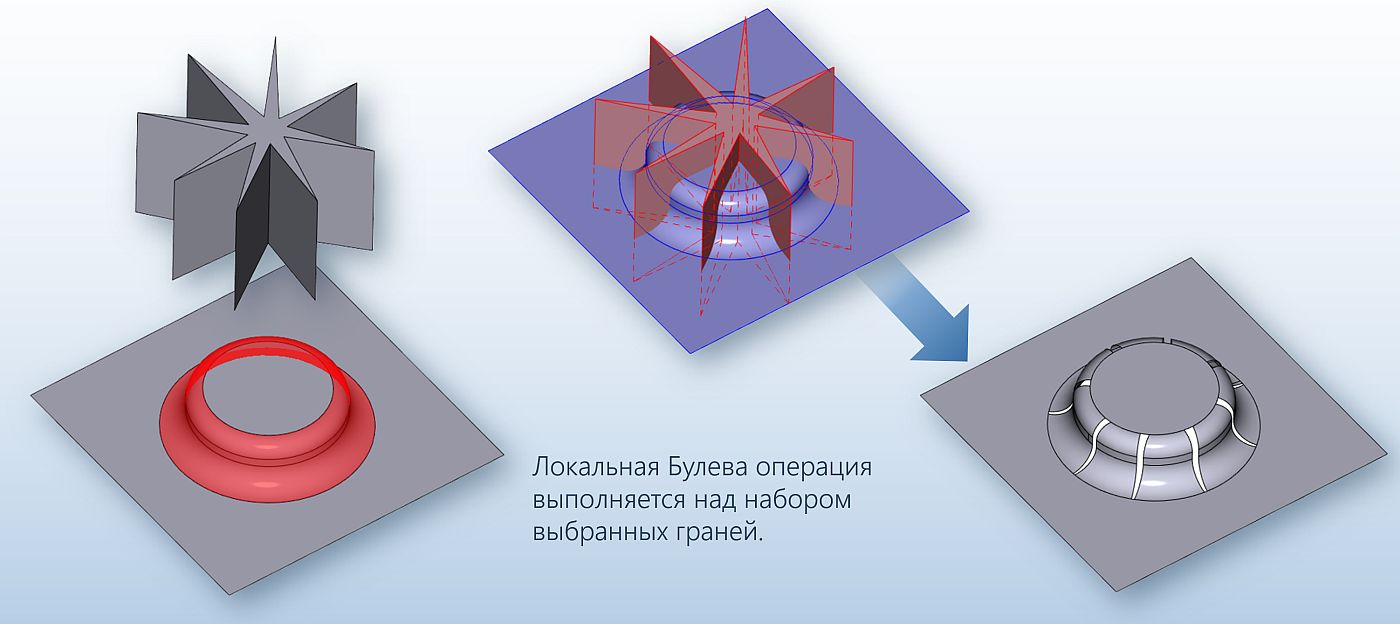
Рис. 29. Локальные булевы операции над заданным набором граней тела

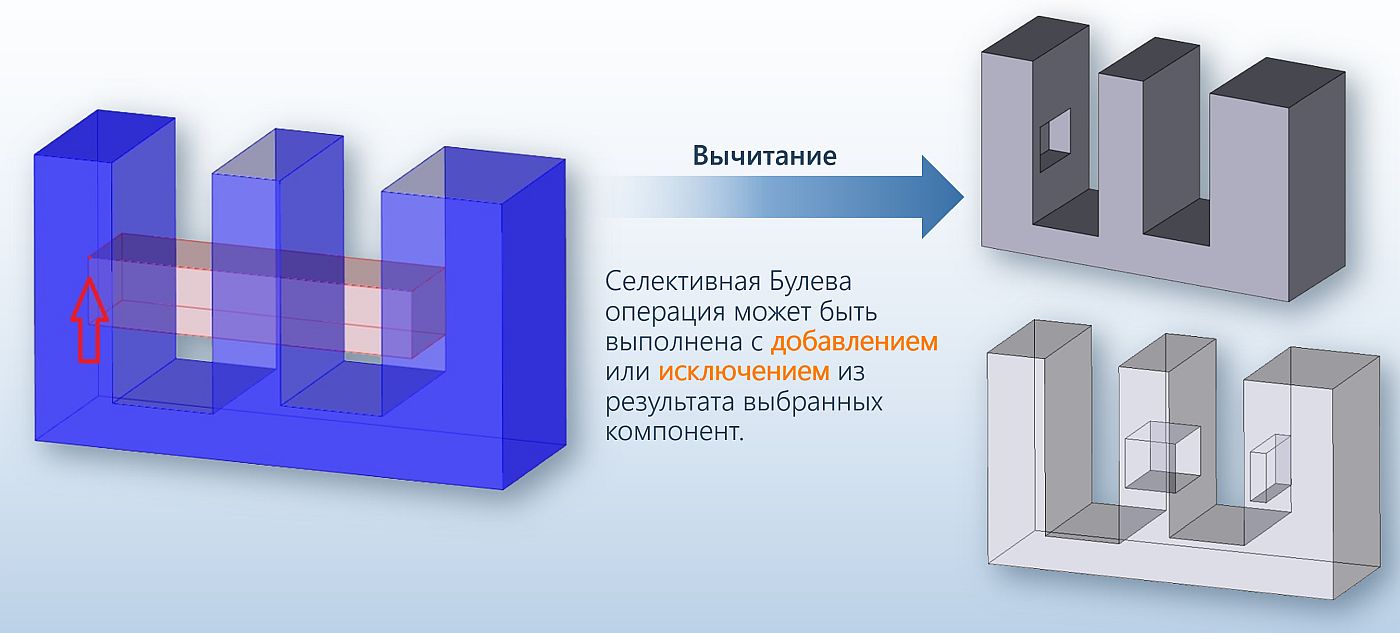
Рис. 30. Селективная булева операция (вычитание)

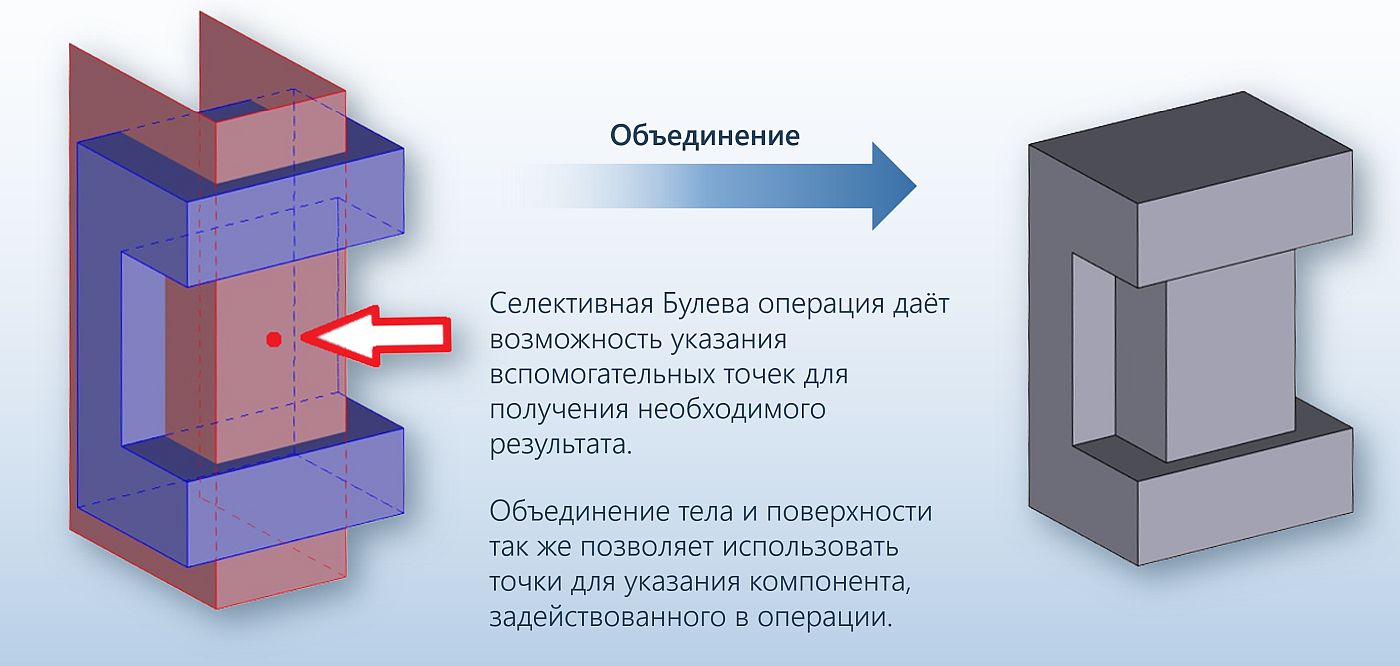
Рис. 31. Селективная булева операция (объединение) над твердым и поверхностным телами

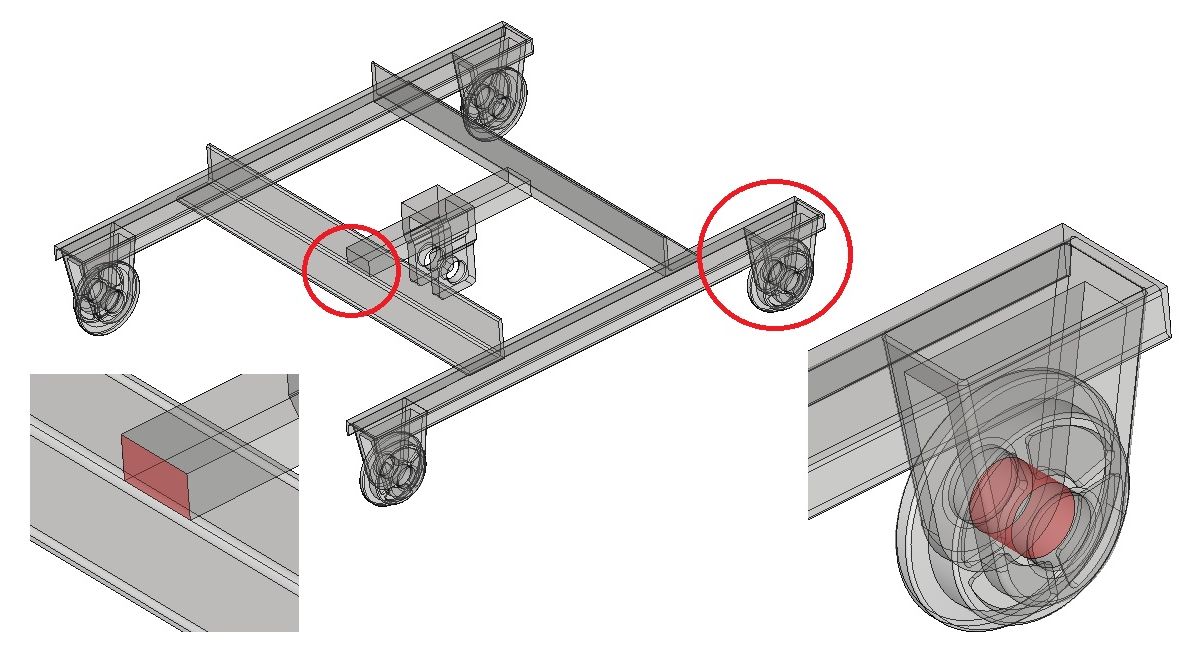
Рис. 32. Обобщенная булева операция (объединение): красным цветом выделены грани контакта

 В наборе инструментов булевых операций поддерживается функциональность по работе с экземплярами тел (instancing) — технике оптимизации булевой операции над массивами тел, геометрия которых отличается только положением экземпляров в пространстве. Кроме того, поддерживаются операции «по образцу» (patterning), когда элементы размножаются по заданной грани (рис. 33).

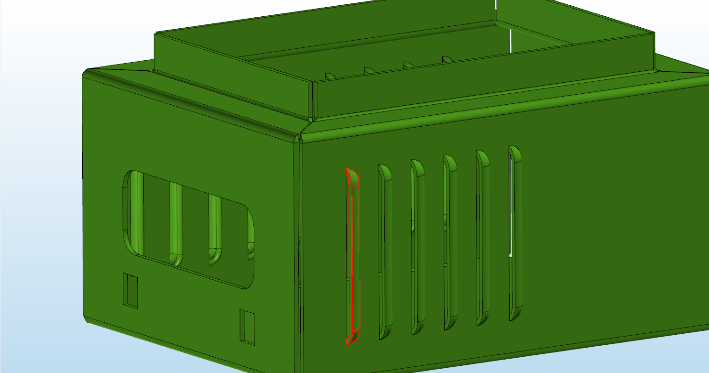
Рис. 33. Размножение граней тела операцией «массив граней» (patterning)

В алгоритмах геометрического ядра повсеместно и активно используются многопоточные вычисления. Эта возможность была заложена в алгоритмы ядра изначально, так как является одним из основных инструментов повышения общей эффективности работы конечного приложения. При этом RGK поддерживает как внутреннее распараллеливание вычислений (когда параллельные потоки запускаются автоматически), так и внешнее (когда параллельные потоки создаются в прикладном коде за пределами функций ядра). Параллельные вычисления позволили на ряде сценариев получить многократный прирост производительности по сравнению с существующими геометрическими ядрами (рис. 34 и 35).

Рис. 34. Пример работы алгоритмов булевых операций RGK

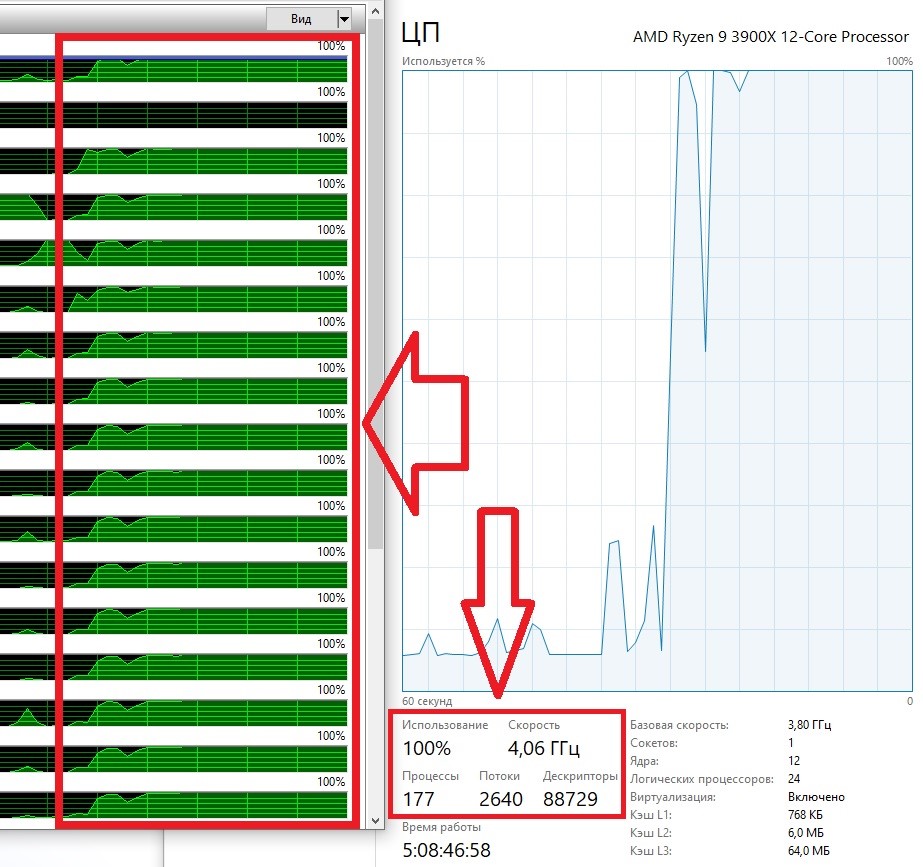
Рис. 35. Характерный график загрузки процессора на задаче с предыдущего рисунка

Похожее поведение наблюдается и на большинстве других вычислительно емких задачах. В частности, на задачах проверки пересечения тел в сборках, расчета расстояний и построения проекций с удаленными невидимыми линями (рис. 36).

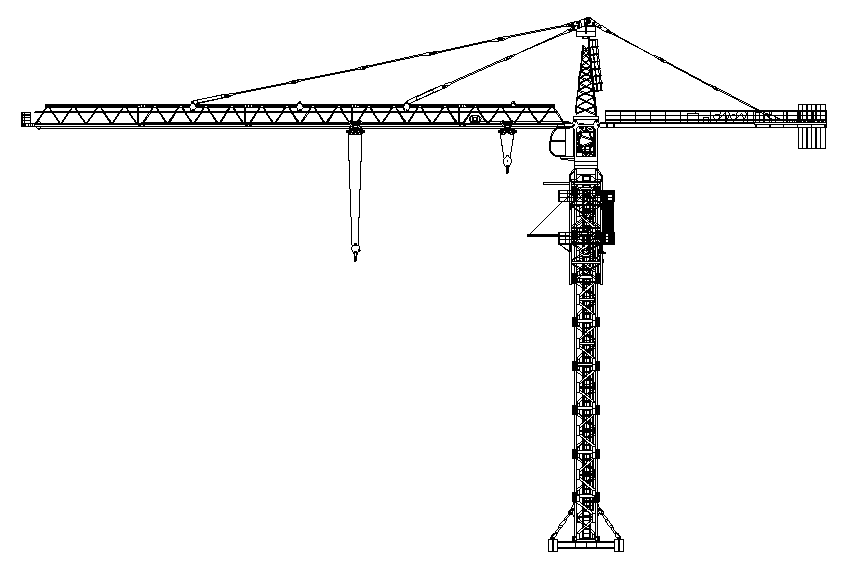
Рис. 36. Проекция с удалением невидимых линий сборки крана 9356 тел и график загрузки процессора на этой задаче

В настоящее время комплект разработчика RGK (SDK) готов к передаче сторонним разработчикам для пробного использования. Желающие попробовать RGK могут обратиться в компанию «Топ Системы».

Помимо работы над самим ядром выполняются связанные работы в T-FLEX CAD 17. В частности, формат RGK (RGK_XML) теперь поддерживается в составе функций импорта/экспорта как через пользовательский интерфейс системы, так и при помощи Open API. Кроме того, доступ к объектам модели (телам, кривым) в формате RGK можно получить, воспользовавшись новыми функциями в составе Open API T-FLEX CAD. Эти функции системы позволяют получить геометрические объекты CAD-системы в формате RGK наиболее удобным способом. Последнее обновление T-FLEX CAD 17 поддерживает эти новые возможности.

Работа над ядром идет высокими темпами, так как компания «Топ Системы» ставит перед собой задачу в максимально короткие сроки достичь уровня существующих западных мировых лидеров в области геометрического моделирования, а возможно, и превзойти этот уровень.