C3D Modeler, или просто геометрическое ядро C3D, — это полностью отечественное программное решение, которое выполняет все возможные вычисления для построения геометрических объектов любой сложности и предоставляет инструменты для проведения операций над этими геометрическими объектами. Основным представлением в геометрическом ядре является граничное представление, однако наряду с граничным поддерживаются полигональное представление и ряд операций с ним. Тела на основе граничного представления, полигональные объекты, а также каркасы могут обладать деревом построения, которое позволяет перестраивать геометрические объекты с новыми параметрами. Наряду с классическими направлениями для геометрического моделирования, такими как каркасное, поверхностное и твердотельное моделирование, в геометрическом ядре C3D интенсивно развиваются направления прямого и полигонального моделирования. Также в состав ядра входит уникальный модуль моделирования тел из листового металла. При этом нашей главной ценностью является команда, которая обладает более чем 20-летним опытом и высоким уровнем экспертизы в геометрическом моделировании (рис. 1).
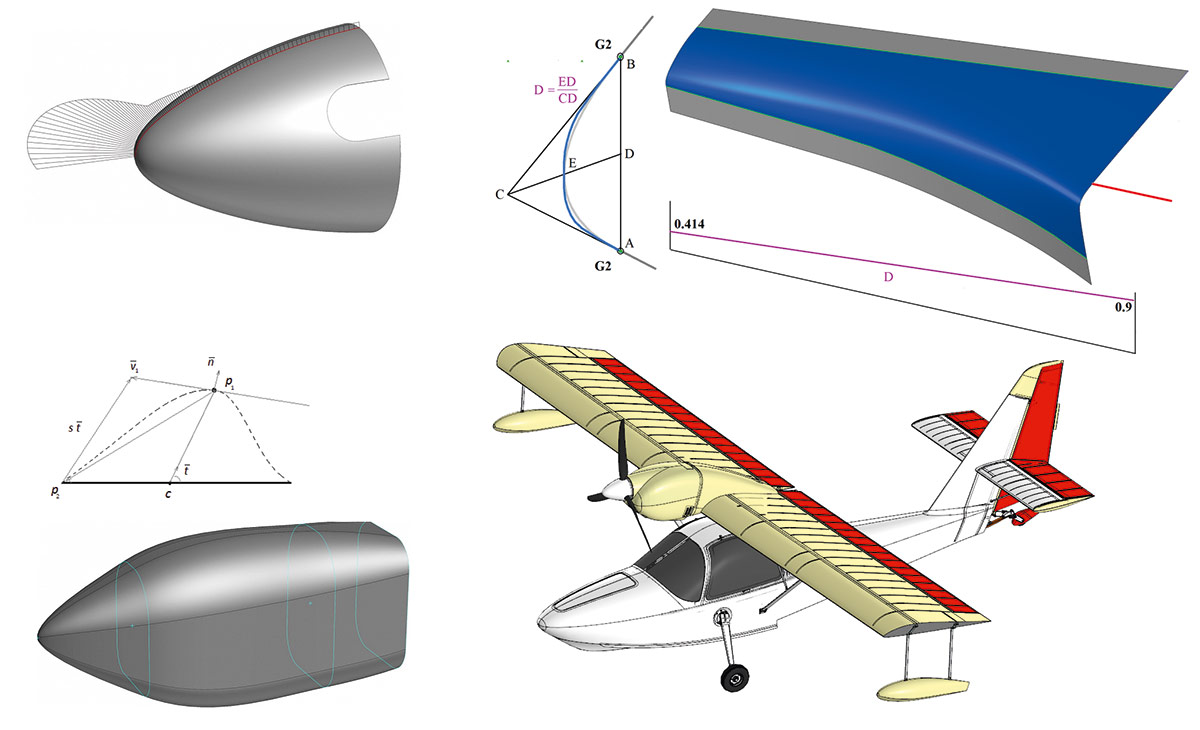
Рис. 1. Геометрическое ядро C3D Modeler
Рассмотрим тенденции развития геометрического ядра C3D Modeler. Трансляция данных неизбежно приводит к потере точности и искажениям в транслируемых объектах. Чтобы последующие операции успешно выполнялись над такими транслируемыми объектами, необходимо, с одной стороны, развивать инструменты диагностики и лечения геометрии, а с другой — учитывать управляемую точность в операциях над этими объектами.
В последнее время существенно выросла значимость прямого моделирования, которое является стратегической областью развития ядра C3D. Это обусловлено в том числе тем фактом, что после ухода западных вендоров осталось достаточно большое число моделей, эффективно изменять которые зачастую можно только средствами прямого моделирования. Мы наблюдаем стабильно высокий рост запросов на инструменты полигонального моделирования. Нашим текущим и потенциальным пользователям в первую очередь интересен функционал по лечению полигональных объектов, а также различные операции с ними. Стабильным остается спрос на инструменты по реверс-инжинирингу полигональных объектов, причем полигональное направление также является стратегической линией развития ядра C3D. Актуален тренд, связанный с усложнением инструментов поверхностного и твердотельного моделирования. Отмечается спрос со стороны клиентов C3D Labs на нетрадиционные для классических CAD-систем инструменты. Например, расчетчикам нужны инструменты построения срединной оболочки на базе твердотельной модели и выделение балочного элемента на основе модели в граничном представлении. Все перечисленные направления являются важными для наших клиентов, а некоторые — критически важными (рис. 2). Мы учитываем сжатые сроки, в которых действуют пользователи, и стремимся оперативно адаптировать продукты и предоставлять им необходимый набор опций.

Рис. 2. Сборка лодочного мотора. Анимация конечного изделия
Обзор изменений в составе геометрического ядра следует начать с каркасного моделирования. За прошедший год команда ядра провела масштабную оптимизацию. Была завершена работа над функционалом продления кривых, а также над методами сворачивания и разворачивания кривых. Ряд доработок коснулся кривой по закону, а именно нового интерфейса создания аналитических функций. Существенным образом была дополнена документация по символьной кривой. Кроме того, пользователи получили возможность опционально сохранять параметризацию кривых при их усечении (рис. 3).

Рис. 3. Доработки и новинки каркасного моделирования
Особое внимание было уделено сбору контуров с учетом толерантности в вершинах в рамках управления точностью в операциях. В интерфейс преобразования кривой в NURBS была добавлена точность преобразования. Яркой новинкой стал функционал построения сглаженной аппроксимации по набору точек, который был анонсирован в прошлом году, но теперь реализован на базе отдельного модуля плавных кривых C3D FairCurves. Одним из усовершенствований в этом модуле стала возможность фиксировать некоторые точки при прохождении сплайна через них.
Ключевая составляющая в функционале каркасного моделирования — построение сглаженной аппроксимации по набору точек. Входными параметрами операции служат максимально допустимое отклонение сплайна от набора точек, порядок сплайна, а также признак его замкнутости. Опционально можно фиксировать некоторые точки, чтобы сплайн проходил точно через них, и в этих фиксированных точках можно также управлять направлением касательной. Влияние сглаживания на построение стандартного авиационного профиля очевидно. Когда сглаживание отсутствует, сплайн четко проходит через заданные точки, однако при этом возникают значительные осцилляции на эпюре радиуса кривизны. Используя сглаживание, можно получить более качественную кривую, сохраняя контроль над точностью прохождения сплайна через опорные точки (рис. 4).
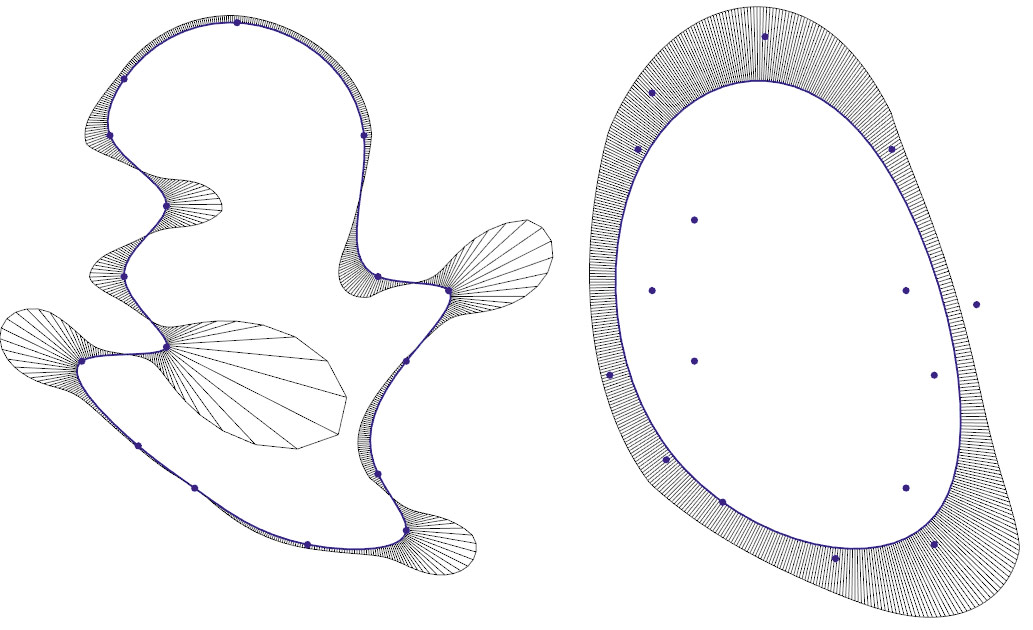
Рис. 4. Доработки и новинки каркасного моделирования
В планах по каркасному моделированию — построение балочной модели на основе твердотельной оболочки, реализация нового функционала построения срединной линии (линии, геометрическое место точек которой равноудалено от двух родительских кривых на плоскости), а также завершение работы по вписыванию отрезка прямой и дуги окружности в набор точек.
К обновлениям в разделе поверхностного моделирования относится доработка расчета производных старших порядков для поверхности переменного конического сечения, оптимизация метода продления оффсетной поверхности и существенный апгрейд операции построения заплатки с сопряжениями на границах (рис. 5).

Рис. 5. Доработки и новинки поверхностного моделирования
Были расширены возможности срединной оболочки. По аналогии с кривыми в метод преобразования поверхности в NURBS добавилось управление точностью преобразования, а само преобразование было значительно модернизировано. Удалось ускорить аппроксимацию изоклин, в том числе за счет оптимального подбора контрольных точек, которые используются для отслеживания точности преобразования. Комплекс предпринятых мер позволил повысить качество преобразования поверхности в NURBS при сохранении модели за минимальное время. Ранее преобразование модели поверхности с неравномерной параметризацией в NURBS приводило к некоторым искажениям. На данный момент эти искажения устранены (рис. 6).

Рис. 6. Доработки срединной оболочки
Наиболее значимым достижением в поверхностном моделировании стало появление новой операции — скругление групп несвязанных граней. Для этой операции была доработана поверхность конического сечения на основе метода движения диска. Диск движется вдоль некоторой заданной опорной кривой, одновременно касаясь двух групп граней, которые могут быть не связаны между собой. При этом есть возможность управлять границами полученной поверхности скругления с учетом того, что радиус этой поверхности может быть переменным, то есть меняться как по линейному, так по кубическому и даже по произвольному закону, заданному на основе некоторой кривой. Также опорная кривая может представлять собой составную кривую, а сама грань скругления — подрезать опорные грани по опорным кривым, чтобы затем осуществить сшивку этих граней в единую оболочку. Параметрами операции можно управлять, чтобы определить сторону, с которой будет построено это скругление (рис. 7). И наконец, само поперечное сечение этой поверхности может представлять собой дугу окружности, дугу эллипса, параболу, гиперболу и вообще любой сплайн, гладко стыкующийся с опорными поверхностями, а также линейный отрезок.
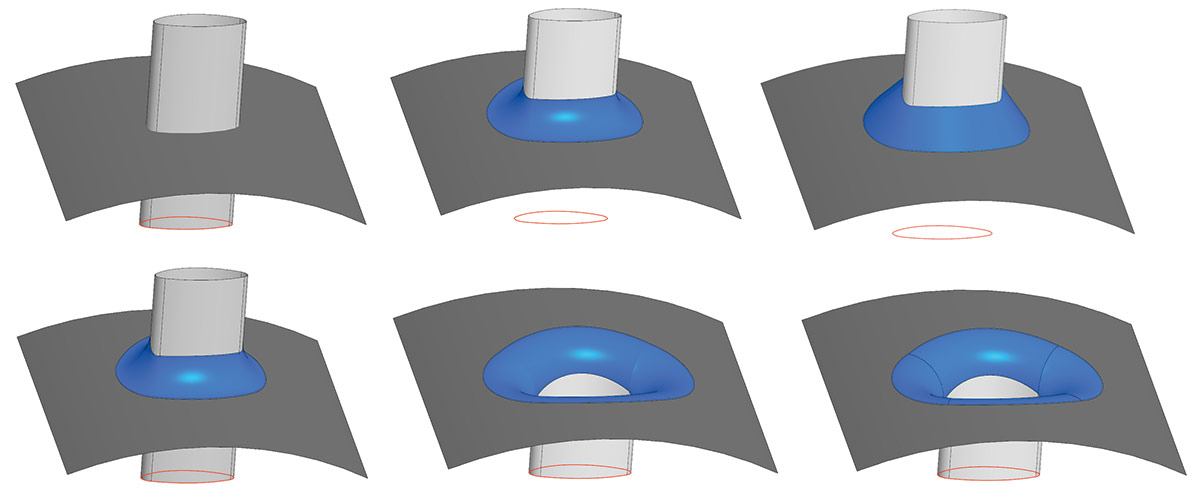
Рис. 7. Поверхность скругления граней
Основные планы по поверхностному моделированию объединяют доработку операций скругления групп несвязанных граней и введение нового функционала продления поверхности по заданному типу, то есть по закону поверхности — касательно прямолинейно и касательно с конечной кривизной. Продолжится работа по разворачиванию поверхности двойной кривизны с учетом разрывов и наложений и по модификации заплатки в отношении сопряжений на ее границах.
Основные изменения в области твердотельного моделирования коснулись уже упомянутой диагностики входного контура на самопересечение в операциях заметания. Кроме того, была добавлена поддержка образующей типа каркаса в операциях заметания и улучшена функция поиска ближайшего тела для операции выдавливания с учетом угла (рис. 8).
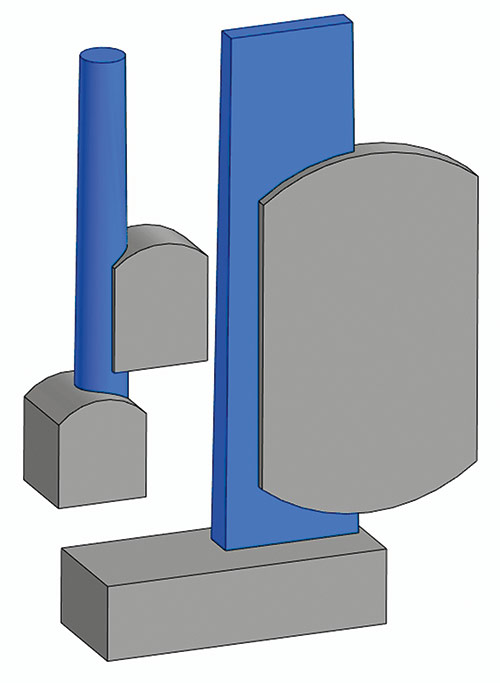
Рис. 8. Доработки и новинки твердотельного моделирования
Была реализована новая операция построения уклона от непрерывной цепочки ребер некоторой грани, причем операция уклона также подверглась трансформации. Была введена диагностика на самопересечение результата этой операции, а также предусмотрены случаи вырождения топологии модели при выполнении операции уклона (рис. 9). В настоящее время ведется интенсивная работа над прототипом операции кинематики с динамически изменяемым сечением. Это означает, что параметры некоторого сечения, которое движется вдоль заданной траектории, могут быть изменены путем наложения на них каких-то функциональных зависимостей. В результате появляется возможность моделировать достаточно сложные формы. Уже упомянутая работа по управлению точностью будет системно вестись на протяжении года. Кроме того, в этот период мы планируем решить поставленные задачи по кинематике с динамическим сечением.
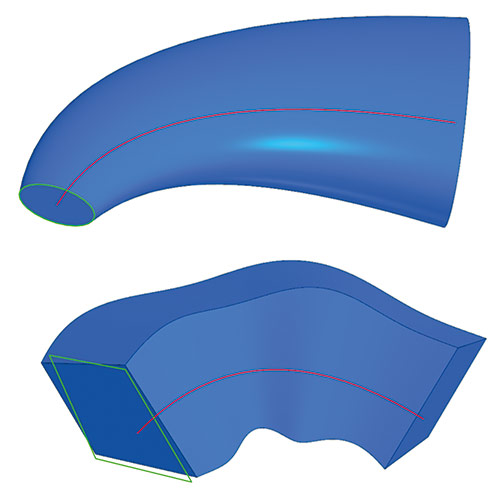
Рис. 9. Операция уклона от ребер
Что касается модуля проецирования, в алгоритме построения плоских проекций в течение года мы работали над улучшением построения линии очерка, с одной стороны, а с другой — над уточнением, разбиением их друг другом. Построение местных разрезов и сечений теперь можно осуществлять гораздо быстрее, а учет неразрезаемых компонентов на местных разрезах и сечениях проводить более эффективно (рис. 10).
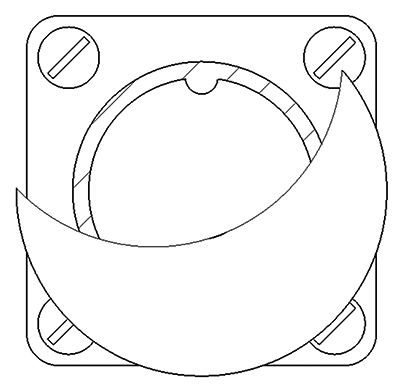
Рис. 10. Алгоритмы построения плоских проекций
Перемены произошли и в построении осевых линий. Главной новинкой модуля построения плоских проекций является возможность проецирования полигональных объектов. Теперь наряду с геометрией в твердотельном представлении на вход алгоритма проецирования можно подавать и полигональные тела, причем набор может быть совершенно разнородным. По полигональным объектам строится линия очерка и учитываются затенения полигональных и твердотельных объектов друг другом (рис. 11). В центре внимания — проецирование границ триангуляции. Если полигональный объект содержит несколько триангуляций, то границы триангуляций тоже нужно уметь проецировать. Мы намерены добиться этого.
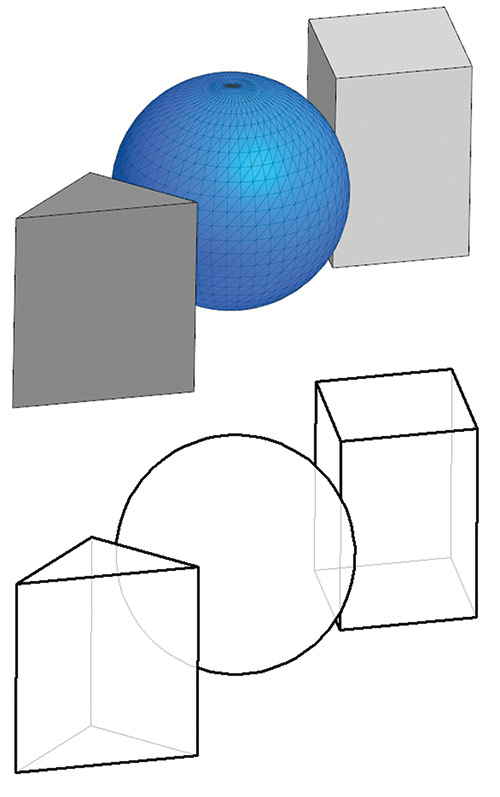
Рис. 11. Проецирование полигональных объектов
Кроме того, над ядром проводился ряд общих или системных работ. Во-первых, продолжается плавный переход на новые интерфейсы наших функций. Внедрен индикатор прогресса в операциях, который, кроме индикации самого процесса, позволяет прерывать длительные операции. Это изменение коснулось как булевых операций, так и построения триангуляций. Во-вторых, мы стремимся повысить потокобезопасность объектов. В числе прочих активностей — защита записи в формат C3D, унификация объектов C3D с STL, за счет которой можно использовать их в range-based циклах, и работа по атрибутам цвета и визуальным эффектам. Появились новые интерфейсы преобразования цвета, новые системные атрибуты — например вектора чисел типа int32, int64 и действительных чисел. Еще одно новшество — функционал измерения расстояния между геометрическими объектами, к примеру кривая — кривая и кривая — поверхность.



