Леонид Бабак
Д.т.н., профессор, кафедра компьютерных систем в управлении и проектировании (КСУП), Томский государственный университет систем управления и радио-электроники.

Алексей Поляков
К.т.н., доцент ОНЦ «Институт высоких технологий» БФУ им. И. Канта, технический директор ООО «Триаксес Лайн».

Илья Волков
Студент ОНЦ «Институт высоких технологий» БФУ им. И. Канта.

Кирилл Жилинский
Студент ОНЦ «Институт высоких технологий» БФУ им. И. Канта.

При построении математических моделей технических объектов (ТО) выделяют управляемые параметры и зависящие от них характеристики (критерии). Как правило, на выходные критерии налагаются ограничения, которые задают область допустимых значений (ОДЗ) параметров. Базовая постановка задачи параметрического синтеза состоит в нахождении любого набора значений управляемых параметров, принадлежащих ОДЗ. Однако часто при поиске значений управляемых параметров стремятся также оптимизировать ТО по одному или нескольким критериям. Для решения такого рода задач разработана программная система IMAGE. Программа помогает исследовать математическую модель устройства, найти допустимые и оптимальные решения. IMAGE реализует подход интерактивного взаимодействия пользователя с графическим представлением ОДЗ, получаемым «методом проекций». Название метода связано с подходом, который позволяет проектировщику составить представление об ОДЗ в многомерном пространстве управляемых параметров математической модели путем построения проекций на привычные двумерные и трехмерные подпространства. При этом на изображении проекции ОДЗ можно также показать прогнозируемые значения критериев. Процесс поиска решений состоит в интерактивном взаимодействии пользователя с изображениями проекций ОДЗ, поэтому используется определение «визуальные вычисления».
В статье приведено краткое описание метода и программной системы; рассматривается пример: задача поиска оптимальных параметров сварной группы нагруженной балки (подробно исследована ранее во многих источниках) и предлагаются новые решения с учетом практической реализуемости изделия.

Определим многомерную область допустимых решений DX системой неравенств:

D_X={X:Y–≤Y(X)≤Y+},   (1)

где Y∈R^m — вектор критериев ТО; X∈Rⁿ — вектор независимых переменных (управляемых параметров) ТО.

Большинство методов численного оптимизационного поиска позволяют проектировщикам получить одно или несколько решений, принадлежащих D_X и с некоторой точностью приближающихся к математическому оптимуму целевой функции. Однако такие решения могут оказаться не всегда «оптимальными» с точки зрения применения их на практике. Достоинство метода проекций [1, 3], реализованного в программной системе IMAGE [2], состоит в том, что проектировщик получает изображение всей области допустимых значений (ОДЗ), а также может оценить поведение целевой функции и других характеристик проектируемого устройства в зависимости от конкретных значений управляемых параметров.

Метод проекций

Метод проекций ОДЗ, предложенный одним из авторов статьи Л.И. Бабаком [1, 3], может быть использован в задачах проектирования технических объектов (ТО) и систем, математическая модель которых представлена в системе неравенств. В связи с тем, что публикаций, рассматривающих метод проекций, сравнительно мало, приведем краткое описание метода.

Для того чтобы описать область D_X одной функцией — сверткой системы неравенств (1), используется R-функция, введенная В.Л. Рвачевым и представляющая собой непрерывный эквивалент булевых функций.

Свойства R(X) : R(X) ≥ 0, X∈D_X; R(X) < 0, X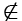D_X; R(X) = 0, X ∈ δD_X где δD_X — граница D_X.

Представим вектор независимых переменных X в виде X = (X1, X[1]) = (xr, xq, X[1]), вектор X1 = (xr, xq) включает компоненты X, определяющие плоскость проекции, а вектор X[1] — все остальные независимые переменные. Проекцией DX1 области DX на плоскость (xr, xq) называется совокупность точек X1 = (xr, xq), обладающих следующим свойством: при X1∈DX1 найдется хотя бы один вектор X[1] такой, что результирующий вектор X = (X1, X[1]) Î DX (рис. 1).

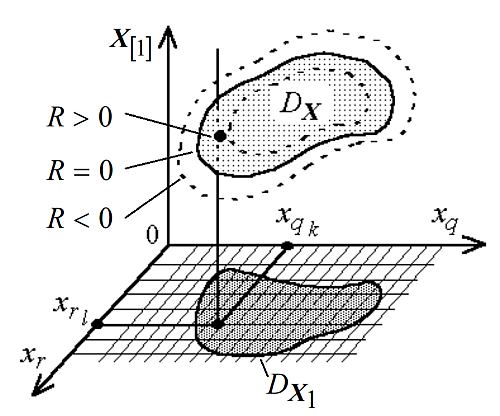
Рис. 1. Схема построения проекции ОДЗ

Алгоритм построения проекции следующий. В плоскости проекции (xr, xq) строится прямоугольная сетка (см. рис. 1), и для каждого узла сетки xrl, xqk решается задача максимизации скалярной функции-свертки R(X) в пространстве остальных компонент X[1] вектора X: найти X *[1](xrl, xqk) = 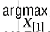R (xrl, xqk, X[1]). Очевидно, что если полученное в узле xrl, xqk максимальное значение R-функции Rmax (xrl, xqk) = maxx1R (xrl, xqk, X[1]) =  R (xrl, xqk, X *[1] (xrl, xqk)) больше или равно нулю, точка X * (xrl, xqk, X *[1] (xrl, xqk)) в n-мерном пространстве принадлежит области DX, а следовательно, точка (xrl, xqk) на плоскости (xr, xq) принадлежит проекции DX1.

Таким образом, на плоскости xr, xq в каждом узле сетки (xrl, xqk) выполняется нахождение значения характеристической B-функции проекции, а совокупность найденных значений образует поверхность B-функции: B (xr, xq) = R (xr, xq, X[1]). Граница проекции находится как линия пересечения полученной  поверхности B-функции с плоскостью B = 0 (рис. 2).

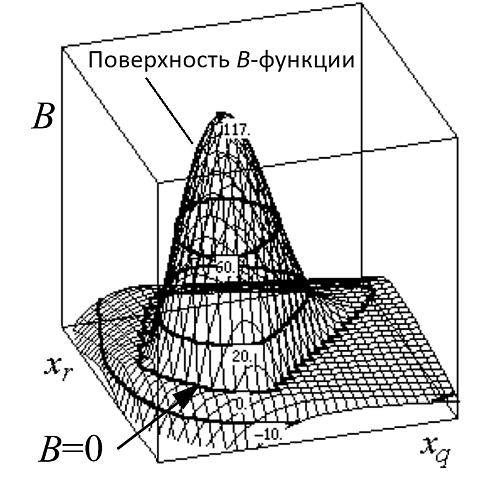
Рис. 2. Пример нахождения границы проекции (линия уровня B=0)

Процесс решения системы неравенств (1) при использовании метода проекций представляет собой последовательную итерационную процедуру, которая включает этапы построения проекции многомерной допустимой области DX на плоскость двух очередных компонент вектора управляемых параметров X и выбора допустимых значений этих компонент в пределах проекции.

Достоинством метода проекций является то, что теоретически он позволяет найти полное множество допустимых решений задачи параметрического синтеза. При этом проектировщику предоставляется информация о прогнозируемых значениях характеристик (критериев) модели. Это позволяет находить решения с учетом многих критериев, в том числе и сложно формализуемых в виде аналитических выражений.

Программная система IMAGE

Метод проекций реализован в программной системе IMAGE [2], разработанной в 1995-2000 годах исследовательской группой сотрудников Томского университета радиоэлектроники (ТУСУР). IMAGE — акроним Interactive MAthematical Graphic Explorer. Нахождение решений в задачах параметрического синтеза востребовано в разных областях инженерной деятельности, поэтому разработка системы возобновлена с участием сотрудников и студентов Балтийского федерального университета (БФУ) им. И. Канта.

Программа имеет модульную структуру и включает следующие части: блоки, реализующие численные методы поиска; модули визуализации; интерпретатор описания задач; подключаемые модули расчета математических моделей; ядро системы, связывающее все компоненты (рис. 3). Такая блочная структура дает гибкость, позволяет независимо разрабатывать отдельные части системы и наращивать функционал.

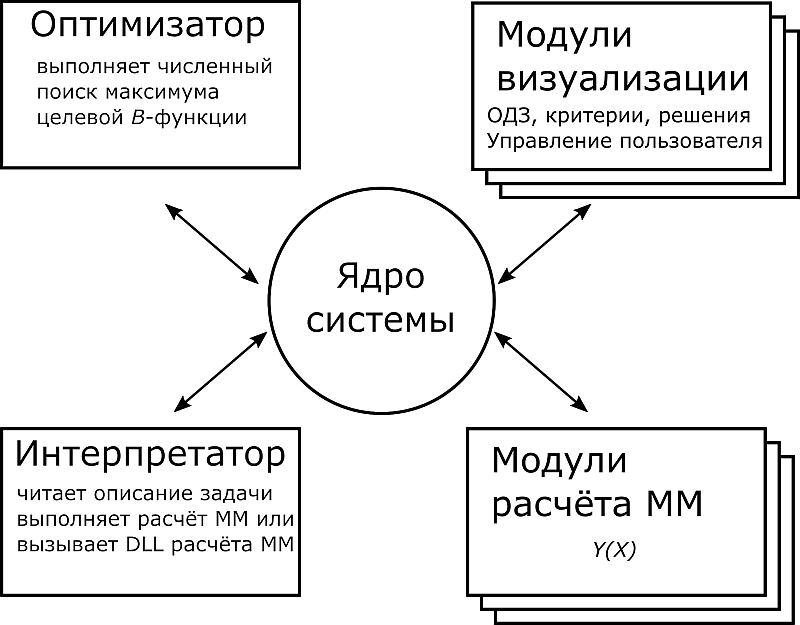
Рис. 3. Модульная структура системы IMAGE

Внешний вид программы показан на рис. 4. Программа позволяет строить проекции многомерных ОДЗ на плоскости (2D-проекции) и трехмерное пространство (3D-проекции), показывать поверхности характеристик и линии уровней прогнозируемых критериев. С использованием программы IMAGE можно выполнить полный процесс поиска допустимых и оптимальных решений в задачах параметрического синтеза.

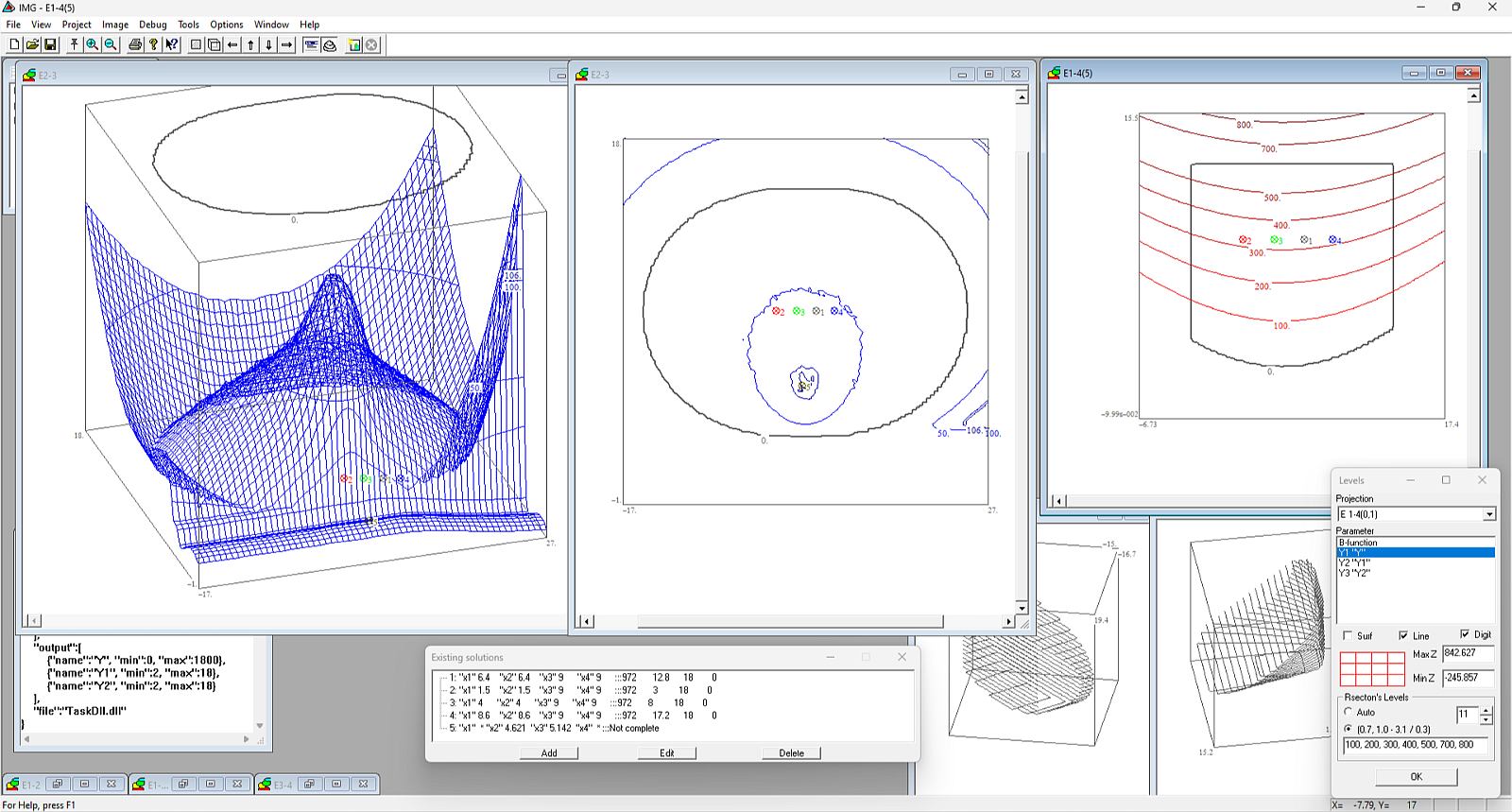
Рис. 4. Внешний вид программы IMAGE при исследовании математической модели с использованием 2D- и 3D-проекций,
а также показом прогнозируемых значений критериев

Пример — поиск параметров нагруженной балки

Проиллюстрируем использование системы IMAGE на примере задачи проектирования нагруженной балки, приведенной в книге [4], — первоначально задача была описана в статье [5]. Достоинство этого примера в том, что он подробно исследован в разных источниках; это дает нам возможность сравнить и проанализировать различные решения. Кроме того, эта задача имеет достаточно простой физический и практический смысл, что облегчает понимание сути предлагаемого подхода.

Задача состоит в нахождении параметров, минимизирующих затраты на изготовление сварной группы нагруженной балки А, приваренной к опоре B (рис. 5). Используем далее обозначения и единицы измерения, приведенные в источнике [4], это позволит сравнить значения решений, полученные разными методами. Длина свободного нагруженного плеча балки L и величина нагрузки  заданы постоянными значениями:  L = 14 дюймов; F = 6000 фунтов.

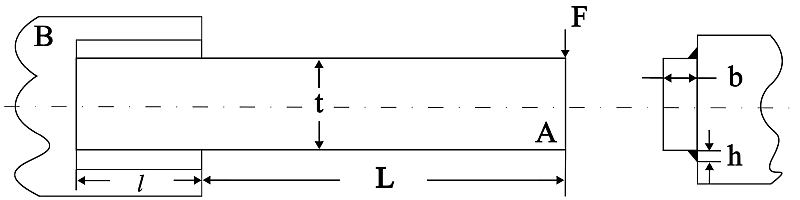
Рис. 5. Схема: нагруженная балка

Приведенная в источнике модель балки имеет четыре переменных (управляемых) параметра, а именно размеры: h — толщина сварного шва, l — длина плеча балки, привариваемого к опоре, t — высота балки, b — толщина балки. В модели эти параметры обозначены как неизвестный вектор X:

X = [h, l, t, b]=[x1, x2, x3, x4].            (2)

Решение задачи состоит в нахождении значений этого вектора переменных при оптимальном значении целевой функции затрат F(X). Приведем сразу итоговый вид целевой функции, которая в источнике выводится из геометрических соотношений и сводится к сумме затрат на производство необходимого объема сварного шва и стоимости материала балки:

F(X) = (c1 + c2) x12 x2 + c3 x3 x4 (L + x2), (3)

где c1 — стоимость сварочных работ кубического дюйма шва; c2 — стоимость материала кубического дюйма шва; c3 — стоимость кубического дюйма материала балки. В [4] приведены значения констант: c1 = 1,0 долл./дюйм3;
c2 = 0,10471 долл./дюйм3; c3 = 0,04811 долл./дюйм3 .

На управляемые параметры налагаются ограничения с учетом физической реализуемости изделия (минимальная ширина сварного шва — 0,125 дюйма; это значение задает и минимальную толщину балки):

0,125 ≤ x1 ≤ 10,0,

0,100 ≤ x2 ≤10,0,                       (4)

0,100 ≤ x3 ≤10,0,

0,125 ≤ x4 ≤10,0.

Модель системы включает следующие ограничения на критерии (расчетные параметры):

Y1 (X) = td – t (X) ≥ 0,

Y2 (X) = sd – s (X) ≥ 0,

Y3 (X) = x4 – x1 ≥ 0,             (5)

Y4 (X) = Pc (X) – F ≥ 0,

Y5 (X) = 0,25 – d(X)≥ 0,

где td — максимальное напряжение в сварном шве при сдвиге: для стали марки 1010 (сталь конструкционная углеродистая качественная) td = 13 600 фунт/дюйм2; t(x) — расчетное напряжение в сварном шве при сдвиге; sd — максимальное нормальное напряжение в балке: sd = 30 000 фунт/дюйм2;
s(x) — расчетное нормальное напряжение в балке; Pc(x) — критическая нагрузка на балку; d (X) — величина прогиба балки.

Напряжение в сварном шве t(x) имеет две составляющие: t'— первичное напряжение в плоскости поперечного сечения сварного шва; t'' — вторичное напряжение при кручении.

t' = F/(2 x1 x2), t'' = MR/J, где M — момент силы F относительно центра тяжести сварной группы; R — размер диагонали от угла балки до центра сварной группы; J — полярный момент инерции сварной группы.

M = F(L + x2/2),

R = 2(x2/2)2 + [(x3 + x1 )/2]2,

J = 1,414 x1 x2 [x22 /12+(x3 + x1)2/4].

t (X) = (t'2 + 2t't''cos q + t''2 )1/2,

где cos q = x2 /(2R).

Напряжение при изгибе балки рассчитывается следующим образом: σ(X) = 6FL/(x4 x32).

Критическая нагрузка на балку описывается следующим выражением:

,

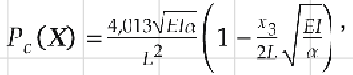где E — модуль Юнга, равный 30·106 фунт/дюйм2, I = x3 x43/12, α = Gx3 x43/3, G — модуль сдвига, равный 12·106 фунт/дюйм2. Прогиб балки: σ(X) = 4FL3/(Ex33 x4).

В статье [5], где была приведена исходная математическая модель, авторы находят решение поставленной задачи путем аналитических преобразований выражений и использования методов геометрического программирования (GP). Найдено оптимальное решение (№ 1, в табл. 1) и выполнено сравнение с результатами, полученными с использованием других методов решения оптимизационных задач (см. табл. 1) [6, 7]:

Таблица 1. Таблица решений

		x1	x2	x3	x4	F(X)	t(X)	s(X)
№	Метод	h	l	t	b	Затраты (долл.)	Напряжение (фунт/дюйм2)	Напряжение (фунт/дюйм2)
1	GP	0,2455	6,196	8,273	0,2455	2,38594	13 600,3	29 995,3
2	ADRANS	0,2393	6,328	8,3695	0,2458	2,41224	13 599,3	29 271,8
3	APPROX	0,2444	6,2189	8,2915	0,2444	2,38154	13 597,7	29 996,0
4	DAVID	0,2434	6,2552	8,2915	0,2444	2,38411	13 596,7	29 996,0
5	MEMGRD	0,2441	6,2273	8,2927	0,2444	2,38219	13 599,5	29 987,3
6	SEEK1	0,3918	4,6154	6,2309	0,4327	3,19729	13 601,4	30 001,4
7	SEEK2	0,2454	6,2148	8,2546	0,2466	2,39313	13 603,9	29 994,8
8	SIMPLX	0,2792	5,6256	7,7512	0,2796	2,53073	13 601,1	30 002,4
9	RANDOM	0,4575	4,7313	5,0853	0,66	4,11856	13 600,3	29 529,3

• GP — оптимальное решение из [5];
• ADRANS — метод адаптивного случайного поиска;
• APPROX  — последовательная линейная аппроксимация Гриффита и Стюарта;
• DAVID — метод Дэвидона — Флетчера — Пауэлла со штрафной функцией;
• MEMGRD — градиентный метод Миля с памятью и функцией штрафа;
• SEEK1 — метод  Хука — Дживса со штрафной функцией;
• SEEK2 — метод  Хука — Дживса с другим видом штрафной функции;
• SIMPLX — симплексный метод со штрафной функцией;
• RANDOM — случайный метод Ричардсона.

Проведем исследование описанной математической модели и полученных решений с помощью метода проекций и программы IMAGE. Для этого математическая модель изделия реализована в виде программного модуля (DLL) на языке C++, подключаемого к программе IMAGE; описание констант и требований к параметрам модели выполнено на языке системы IMAGE с использованием текстового формата JSON. Модель имеет четыре управляемых параметра (2), расчетные параметры и целевая функция реализованы в виде выходных параметров (критериев). Ограничения на управляемые параметры (4) и критерии (5) задают область допустимых значений (ОДЗ) DX в четырехмерном пространстве управляемых параметров.

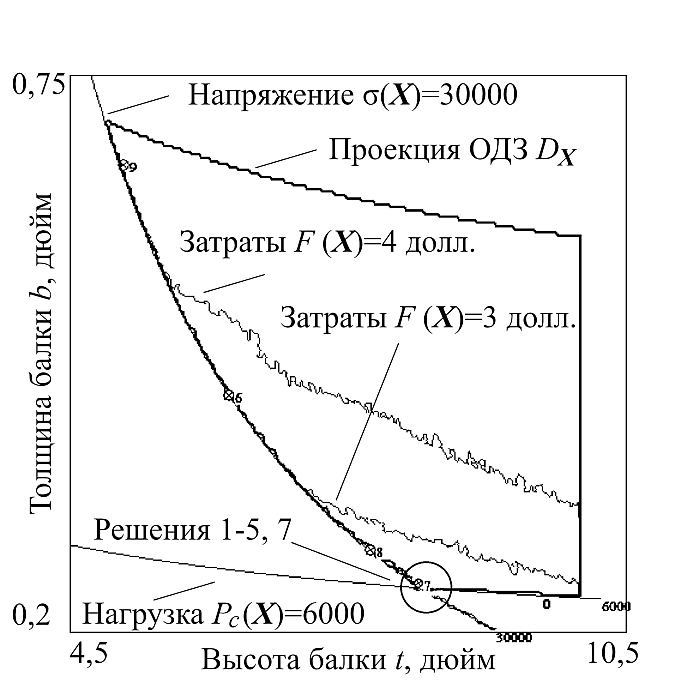
Рис. 6. Проекция t-b

На первом этапе исследования построим проекции DX на подпространства (плоскости) пар управляемых параметров. Изображения получены программой IMAGE: проекция на плоскость параметров t и b (рис. 6), проекция на плоскость параметров h и b (рис. 7), проекция на плоскость параметров h и l (рис. 8). На изображениях также показаны линии уровня расчетных параметров и решения из табл. 1 (показаны пронумерованными точками). Из рис. 6 видно, что все решения, приведенные в табл. 1, лежат на границе проекции ОДЗ DX вблизи максимального нормального напряжения в балке: sd = 30 000 фунт/дюйм2 и минимального значения выдерживаемой нагрузки Pc(X) = 6000 фунтов. На построенных проекциях также выведены линии уровня прогнозируемого расчетного параметра — функции затрат F(X): наглядно показано, что решения 1-5 и 7 сконцентрированы в одном месте на границе допустимой области, ограниченной требованиями к величине нагрузки F и максимальному нормальному напряжению в балке sd, где достигается минимальное значение цены. Значения 8, 6, 9 далеки от региона с минимальным прогнозируемым уровнем затрат. На проекции h-b (см. рис. 7) видно, что решения с минимальными значениями функции затрат F(X) лежат на границе условия физической реализуемости g3(X) из набора ограничений (4) — это условие определяет, что толщина сварного шва не может быть больше толщины балки. Проекция h-l (см. рис. 8) показывает, что предложенные решения лежат относительно далеко от границ ограничений на эти управляемые параметры.

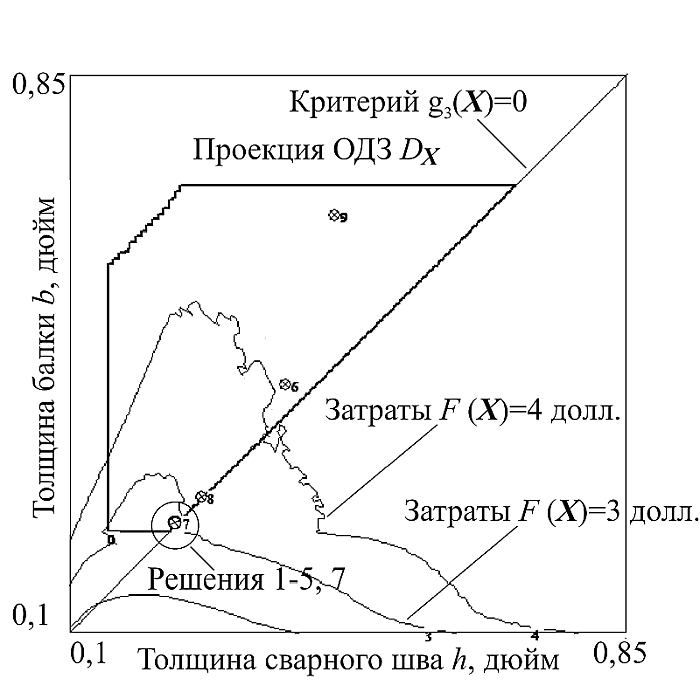
Рис. 7. Проекция h-b

При этом, так как решения лежат на границе ОДЗ, что видно из рис. 6 и 7, минимальное отклонение значений управляемых параметров приводит к тому, что решения становятся недопустимыми. Как показано в табл. 1, параметры t(x) — расчетное напряжение в сварном шве при сдвиге и s(x) — расчетное нормальное напряжение в балке, вычисленные для ряда решений (решения 1, 6-9), приведенных в [5], выходят за пределы ограничений (в табл. 1 такие значения выделены жирным шрифтом). Возможно, это связано с округлениями значений управляемых параметров или ошибками в программной реализации методов, которые были использованы авторами.

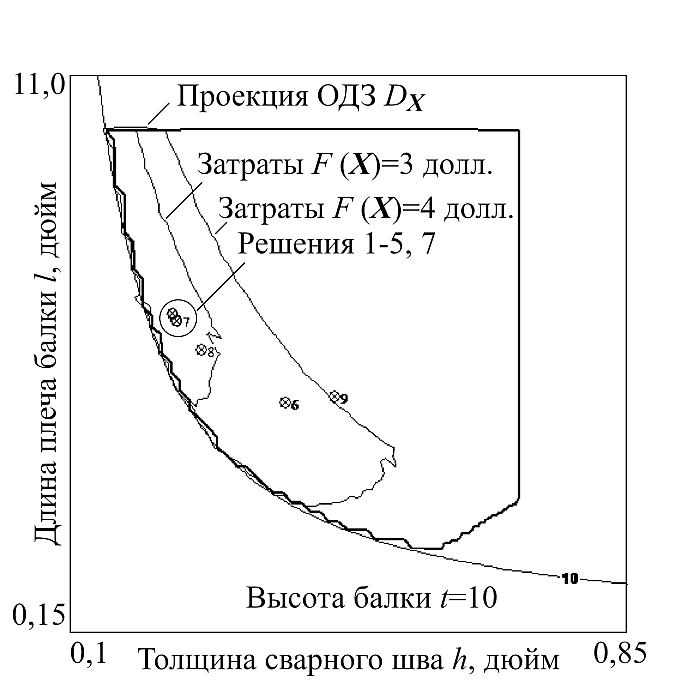
Рис. 8. Проекция h-l

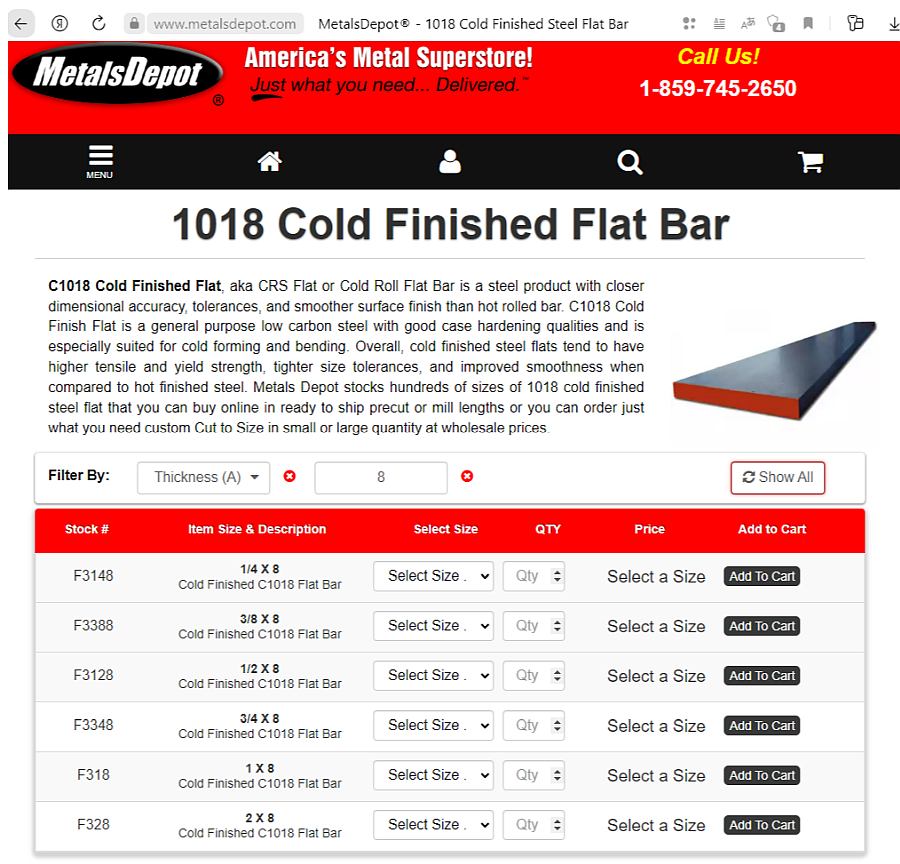
Рис. 9. Страница веб-сайта поставщика металлоизделий в США: https://www.metalsdepot.com/

Таблица 2. Таблица решений

№	Метод	x1	x2	x3	x4	F(X)	t(X)	s(X)
		h	l	t	b	Затраты (долл.)	Напряжение (фунт/дюйм2)	Напряжение (фунт/дюйм2)
1	DAVID	0,2444	6,2187	8,2915	0,2444	2,38151	13 598	29 996

Еще одно решение, найденное методом численного поиска Дэвидона — Флетчера — Пауэлла,  приводится в [4] и имеет значения управляемых параметров, приведенные в табл. 2. Нетрудно видеть, что найденное решение близко по своим значениям переменных и расчетных параметров (критериям) к решениям 3-5 из табл. 1 и также лежит на границе ОДЗ DX.

Формально решение 1 из табл. 2 является минимальным из рассмотренных по значению целевой функции затрат F(X): 2,38151 долл. против 2,38154 долл. (решение 3, табл. 1), то есть получен выигрыш в 0,00003 долл. (что составляет примерно 0,001% от цены). Авторы [4] отмечают, что работа над совершенствованием метода Дэвидона — Флетчера — Пауэлла далека от завершения.

Однако формально оптимальное значение может оказаться на практике не всегда приемлемым. Вернемся к сути задачи — минимизации цены изделия, а именно стальной балки, приваренной к опоре. Как можно видеть, приведенные выше решения конкурируют в достижении минимальной цены, изменяя управляемые параметры (размеры стальной балки и толщину сварного шва) в четвертом знаке после запятой на границе ОДЗ, причем некоторые решения не соответствуют ограничениям модели. При этом совершенно очевидно, что работы по изготовлению изделия с такой точностью будут стоить существенно дороже цены материала, которая лежит в основе формирования целевой функции в данной модели.

Иначе говоря, нахождение оптимума при таком подходе может оказаться математическим и алгоритмическим упражнением, имеющим мало практического смысла, так как любой производитель работ по привариванию балок к опоре скажет, что не бывает у поставщиков материалов с произвольными параметрами металлопроката, а изготовить сварной шов с точностью до четвертого знака после запятой — это весьма сложная задача даже для мастера высочайшей квалификации.

Однако приведенная модель может стать весьма полезной при использовании метода проекций, который позволяет нам видеть всю область допустимых значений управляемых параметров и делать прогноз значений критериев.

Рассмотрим, как данная задача может быть решена в случае применения метода проекций.

Металлопрокат на сталелитейных предприятиях изготавливается в ряде стандартизированных размеров профиля (толщина и ширина), при этом длина материала выбирается/нарезается уже из требований конкретного изделия. Поэтому на первом этапе нам надо определиться с оптимальными значениями t — высоты (ширины) и b — толщины балки. Итак, выполним следующие шаги:

1 Подбор материалов. Обратимся к первому же веб-сайту, предлагающему металлопрокат [8], и посмотрим, какие размеры имеются в продаже (рис. 9). Изделий из стали марки 1010 у данного поставщика в предложении не оказалось, но есть близкая по характеристикам марка 1018, причем предложенные размеры подходят для нашей задачи. Материалы предлагаются толщиной: 1/4, 3/8, 1/2, 3/4 дюйма и др., при этом различной ширины; нужную длину можно подобрать из предложенных вариантов или заказать требуемую.

Примечание к рис. 9. Отметим, что поставщик выбран путем поиска в Интернете — вероятно, могут найтись и другие. Поскольку нам важно проиллюстрировать метод, выбор конкретного поставщика в данном случае не важен, так как наша цель — продемонстрировать принципиальный подход. Раз задача из американской публикации, то и поставщик выбран из США.

2 Исследование модели. Построим проекцию ОДЗ на плоскость параметров сочетания t — высоты и b — толщины (рис. 10). Отобразим на проекции несколько линий уровня прогнозируемых затрат F(X). Отобразим на построенной проекции варианты сочетаний  ширины и толщины, которые имеются у данного поставщика.

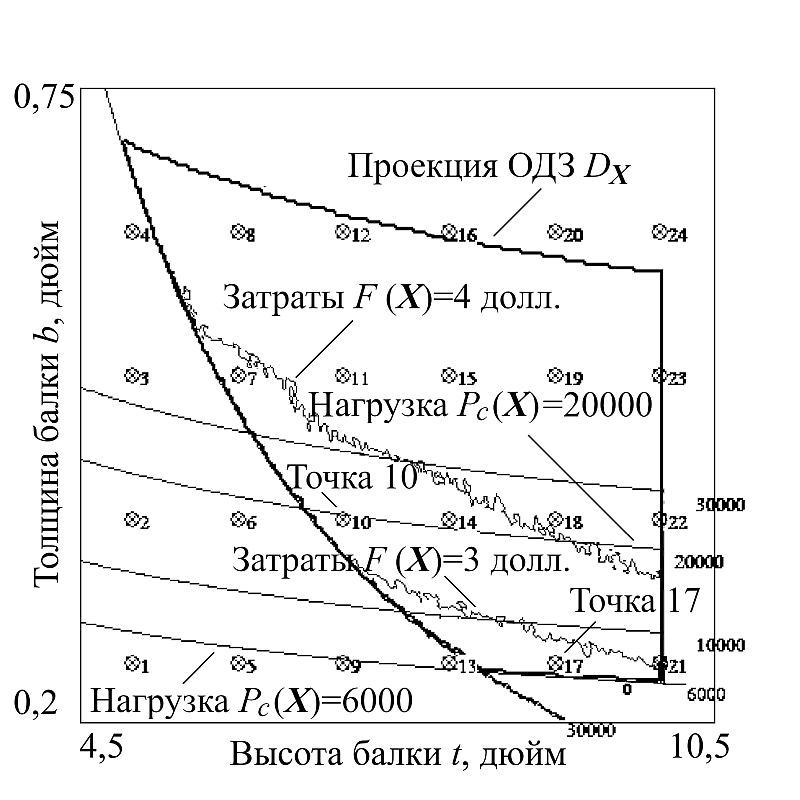
Рис. 10. Проекция t-b

Можно было бы, ориентируясь на значения размеров и линий уровня затрат, сразу выбрать наиболее близкое к оптимуму решение из числа предлагаемых поставщиком сочетаний размеров, но «для полноты картины» покажем на рисунке ряд доступных размеров (варианты пронумерованы от 1 до 24), которые попадают и находятся вблизи проекции ОДЗ.

3 Выбор оптимального по цене решения. Как видно из рис. 10, достаточно много доступных вариантов сочетаний толщины и ширины материала попадает в проекцию ОДЗ. Обратим внимание на линии уровня расчетных прогнозируемых затрат F(X). Ориентируясь на поведение линий уровня затрат, легко сделать вывод, что из числа вариантов, попавших в проекцию ОДЗ, точка с номером 17 (t = 9 дюймов, b = 1/4 дюйма) обеспечит минимальные затраты при выполнении требований к изделию. Зафиксируем пару значений t и b в точке 17 и построим проекцию на плоскость двух оставшихся свободными переменных (h — толщину сварного шва и l — длину плеча балки, привариваемого к опоре), рис. 11. Построим линии уровня затрат F(X) на проекции h-l (17). Параметры h и l мы уже можем выбирать свободно, поэтому зафиксируем эти значения в точке проекции ОДЗ с минимальным уровнем затрат. В результате получено наше Решение 1 в табл. 3.

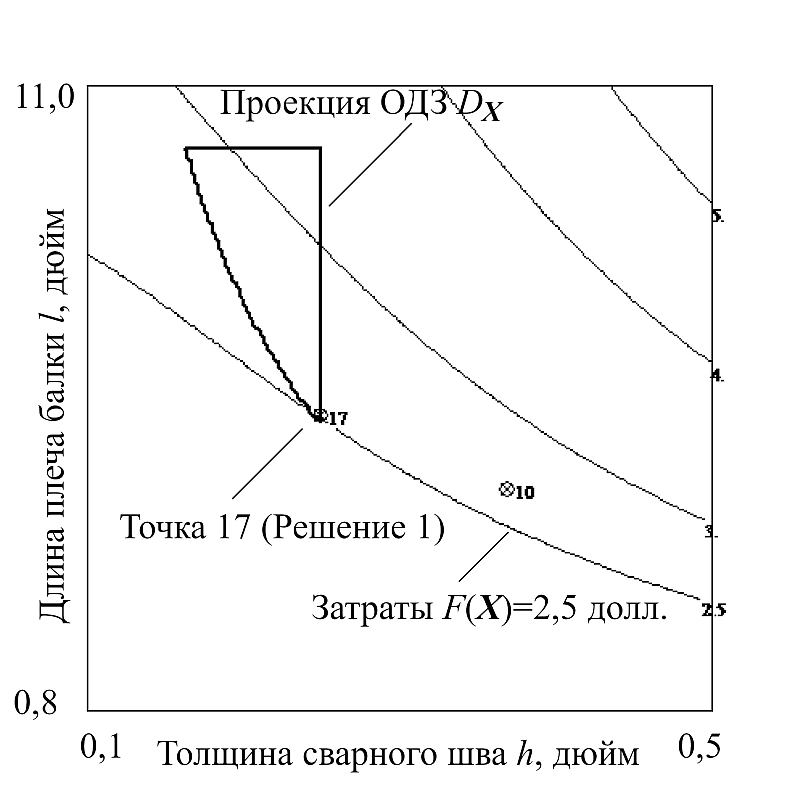
Рис. 11. Проекция h-l (17)

Примечание. Надо отметить, что расположение проекции ОДЗ на рис. 11 и 12 отличается. Это связано с тем, что при задании конкретных значений t и b ОДЗ оставшихся свободных переменных h и l меняет свой размер и положение. Поэтому в обозначении проекции мы указываем, при каких выбранных значениях t и b она построена (в скобках приведен номер выбранной точки): h-l (17) и h-l (10) соответственно.

4 Решение с учетом многих критериев. На проекции рис. 10 также показаны линии уровня расчетной выдерживаемой нагрузки Pc (X); обращает на себя внимание тот факт, что одна и та же выдерживаемая нагрузка может быть обеспечена с разным уровнем затрат. Допустим, что помимо снижения затрат нам также необходимо обеспечить запас по выдерживаемой нагрузке. Тогда рациональным решением будет выбрать значения t и b в точке с номером 10 (t = 7 дюймов, b = 3/8 дюйма). Зафиксируем пару значений t и b в точке 10, построим проекцию на плоскость свободных переменных h-l и отобразим линии уровня затрат F(X) —рис. 12. Затем, выберем значения h и l в точке проекции ОДЗ с минимальным уровнем затрат. В результате получено наше Решение 2 в табл. 3.

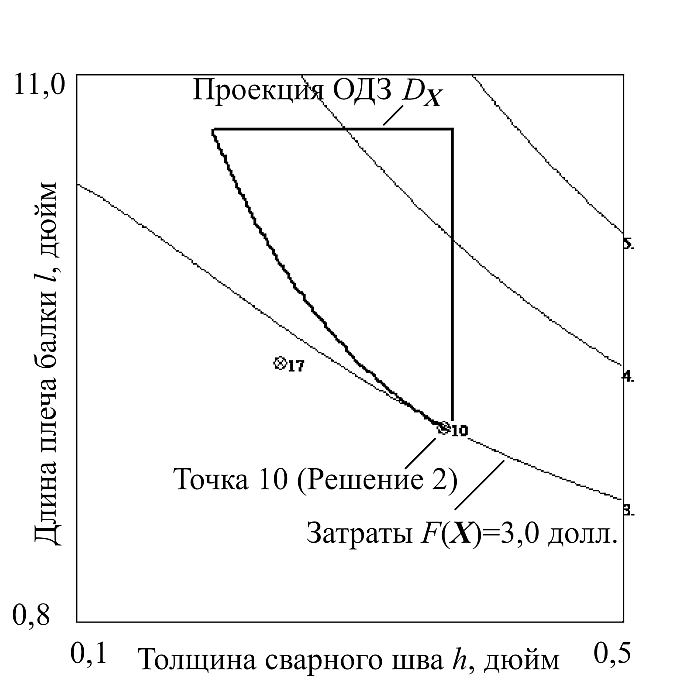
Рис. 12. Проекция h-l (10)

Анализ результатов и выводы

Итого: решение 1 из табл. 3 дает нам сочетание параметров балки, которое обеспечивает расчетный уровень затрат F(X) = 2,51 долл. (что формально на 5% выше, чем решение 1 из табл. 2: F(X) = 2,38 долл.). При необходимости метод проекций позволяет найти решение, отвечающее нескольким критериям. Так, решение 2 из табл. 3 почти в три раза (на 282%) повышает выдерживаемую нагрузку, затраты же возрастают на 19-20% до 3,0 долл. При этом все прочие требования к изделию выполняются.

Таблица 3. Таблица решений

		x1	x2	x3	x4	F(X)	Pc(X)	t(X)	s(X)
№	Метод	h	l	t	b	Затраты (долл.)	Нагрузка (фунт)	Напряжение (фунт/дюйм2)	Напряжение (фунт/дюйм2)
1	Метод проекций	0,25	5,6	9,0	0,25	2,50830	6791,3	13 293,5	24 888,9
2	Метод проекций	0,37	4,4	7,0	0,375	2,98915	19 176,7	13 451,3	27 428,6

Найденные с помощью метода проекций решения табл. 3 по значению целевой функции лучше некоторых решений, приведенных в табл. 1, однако формально уступают лучшим вариантам решений из [4, 5]. При этом решения, найденные с помощью метода проекций и программы IMAGE, имеют несомненное преимущество — они практически реализуемы из материалов, выпускаемых промышленностью и доступных для применения.

Таким образом, использование метода проекций при решении задач параметрического синтеза устройств позволяет получить полное пространство ОДЗ, средства визуализации программы IMAGE облегчают анализ множества вариантов решений и позволяют выполнить оптимальное проектирование с учетом многих критериев.

В данной статье рассмотрена задача из технической области проектирования конструкций, однако подобные задачи встречаются и во многих других областях. Программа IMAGE может применяться как самостоятельный инструмент для решения задач поиска допустимых и оптимальных управляемых параметров устройств и систем. Кроме того, реализация рассмотренного метода проекций может войти как модуль в более крупные САПР. Также отметим, что разрабатывается веб-версия программной системы по адресу www.impro.su. Авторы приглашают к сотрудничеству для решения новых задач проектирования и разработки вариантов использования рассмотренного метода.

Список литературы:

1. Бабак Л.И. Синтез технических устройств и систем с использованием проекций области работоспособности // Док. междунар. симп. СИБКОНВЕРС’97. Томск: 1997. С. 203-213.
2. Бабак Л.И., Поляков А.Ю. Система визуальных вычислений Image для решения математических и технико-экономических задач // Докл. междунар. симп. СИБКОНВЕРС’99. Томск, 1999.
3. Бабак Л.И. «Визуальные» вычисления: решение систем нелинейных неравенств и многокритериальных проблем // Вестник Томского государственного педагогического университета. Томск, 2005. URL: https://cyberleninka.ru/article/n/vizualnye-vychisleniya-reshenie-sistem-nelineynyh-neravenstv-i-mnogokriterialnyh-problem (дата обращения 14.11.2023).
4. Реклейтис Г., Рейвиндран А., Рэгсдел К. Оптимизация в технике. В 2-х кн. Кн.1 // M.: Мир, 1986.
5. Ragsdell, K.M., & Phillips, D.T. Optimal Design of a Class of Welded Structures Using Geometric Programming // Journal of Engineering for Industry, 1976, 98(3), 1021. URL: https://www.sci-hub.ru/10.1115/1.3438995 (дата обращения 21.10.2023).
6. Мицель А.А. Методы оптимизации. В 2-х ч. Ч. 1: учеб. пособие / А.А. Мицель, А.А. Шелестов, В.В. Романенко. Томск: Изд-во Томск. гос. ун-та систем упр. и радиоэлектроники, 2020. 350 с.
7. Шарый С.П. Курс вычислительных методов. Новосибирск: Изд-во Новосиб. гос. ун-та, 2023. 696 с. URL: http://mathscinet.ru/files/SShary.pdf (дата обращения 21.10.2023).
8. Metals Depot — America’s Metal Superstore. URL: https://www.metalsdepot.com/ (дата обращения 21.10.2023).