Моделирование движения и столкновений твердых тел произвольной формы совместно с аэрогидродинамическим расчетом в CAE-пакете FlowVision

Павел Чеботарёв,
Санкт-Петербургский государственный университет, магистр; ООО «ТЕСИС», инженер-программист

Андрей Петров,
ООО «ТЕСИС», руководитель обособленного предприятия в Санкт-Петербурге

Вступление. 30 лет на ниве цифровизации производства в России

В 2024 году компании ТЕСИС, разработчику и поставщику инженерных программных решений и услуг, исполняется 30 лет. Три десятилетия мы помогаем производственным компаниям, конструкторским бюро и научным организациям повышать эффективность, надежность и экономичность своих продуктов.

Мы приглашаем инженеров, конструкторов и технологов посетить крупный форум об инженерном анализе «День FlowVision», который приурочен к юбилею компании. В рамках мероприятия пройдут шесть конференций, посвященных применению отечественного CAE-инструмента в следующих отраслях промышленности:

• авиация и ракетостроение;
• судостроение;
• турбомашиностроение и двигателестроение;
• атомная энергетика;
• моделирование технологических процессов;
• общая секция.

Моделирование движения и столкновений твердых подвижных тел играет важную роль в решении научных и инженерных задач во многих областях техники. В данной статье представлены основные реализованные идеи и краткое описание алгоритмов для моделирования динамики твердого тела в междисциплинарном CAE-пакете FlowVision. Основными требованиями к проведенной работе были высокая точность определения времени и места столкновения твердых тел в процессе аэрогидродинамического расчета и относительно высокая скорость разработанного алгоритма. Следует также отметить, что возможность моделирования столкновений твердых тел существенно расширяет класс решаемых задач для рассматриваемого CAE-пакета.

Описание движения и расчета столкновений твердого тела

В данной работе движение твердого тела описывается законом движения Ньютона в декартовой системе координат относительно его центра масс.

Как правило, для моделирования движения твердого тела достаточно определить его как набор точек пространства, закрепленных в системе отсчета одной точки пространства, называемой центром масс или центром инерции этого твердого тела [1]. Движение твердого тела в пространстве можно разделить на вращательную и поступательную составляющие. При этом будем считать, что вращательная составляющая движения описывается вращением тела вокруг некоторой мгновенной оси, проходящей через его центр масс. Таким образом, зная поступательную и угловую скорость тела, можно рассчитать положение всех его точек в рассматриваемый момент времени (для этого также потребуется найти матрицу поворота).

Пусть нам известны аэрогидродинамические силы, действующие на тело во всех его точках. Тогда, чтобы найти поступательное и угловое ускорение этого твердого тела, достаточно найти полную силу и полный момент силы, действующий на тело в системе его центра масс, а затем воспользоваться уравнениями Эйлера — Ньютона для углового и поступательного ускорения. Найдя эти величины, можно получить соответствующие скорости с помощью простого численного интегрирования.

Расчет характеристик движения твердых тел при столкновении основан на законе сохранения импульса и энергии и в общем случае характеризуется коэффициентом восстановления. Если этот коэффициент равен единице, то столкновение считается абсолютно упругим, а если нулю — абсолютно неупругим (следует также уточнить, что для абсолютно неупругого удара необходимо рассчитать новый общий тензор инерции результирующего тела).

Алгоритм поиска наименьшего расстояния между двумя телами произвольной формы

В сфере научного моделирования твердое тело, как правило, имеет вид сложной поверхности, состоящей из плоских треугольников, называемых фасетками. Геометрия, описывающая такое твердое тело, обычно хранится в бинарных или текстовых файлах определенного формата (STL, VRML и др.) и представляет собой пронумерованный набор точек в трехмерном пространстве, отвечающих вершинам рассматриваемого твердого тела, а также набор кортежей номеров точек — таких, что каждый кортеж соответствует отдельной грани рассматриваемого тела.

Подобный способ описания твердого тела отлично коррелирует с его определением, введенным ранее. Таким образом, будем считать, что вершины рассматриваемого твердого тела заданы и являются точками этого твердого тела, а его поверхности — треугольными фасетками соответствующей трехмерной модели. В таком случае достаточно легко провести декомпозицию задачи нахождения наименьшего расстояния между парой таких твердых тел и сначала решить задачу поиска наименьшего расстояния между двумя плоскими треугольниками в евклидовом пространстве.

Для разработки алгоритма поиска наименьшего расстояния между двумя плоскими треугольниками в евклидовом пространстве можно рассмотреть два общих случая касания таких треугольников:

1.  «Ребро в ребро»: касание ребром плоского треугольника ребра другого плоского треугольника.
2.  «Вершина в грань»: касание плоским треугольником плоскости другого плоского треугольника одной из своих вершин.

Рассматривая представленные возможные случаи касания двух плоских треугольников в трехмерном пространстве, можно кратко описать алгоритм поиска наименьшего расстояния между ними:

1. Найти ближайшие точки, а следовательно, расстояния между всеми ребрами этих треугольников (всего девять измерений).
2. Проверить все вершины каждого из треугольников на предмет попадания перпендикуляра, опущенного из них на плоскость другого треугольника, в грань другого треугольника (всего шесть измерений).
3. Сравнить все полученные расстояния и выбрать минимальное.

Подробный алгоритм решения поставленной задачи может быть реализован без особых трудностей средствами аналитической геометрии [2]. Результат работы алгоритма представлен на рис. 1.

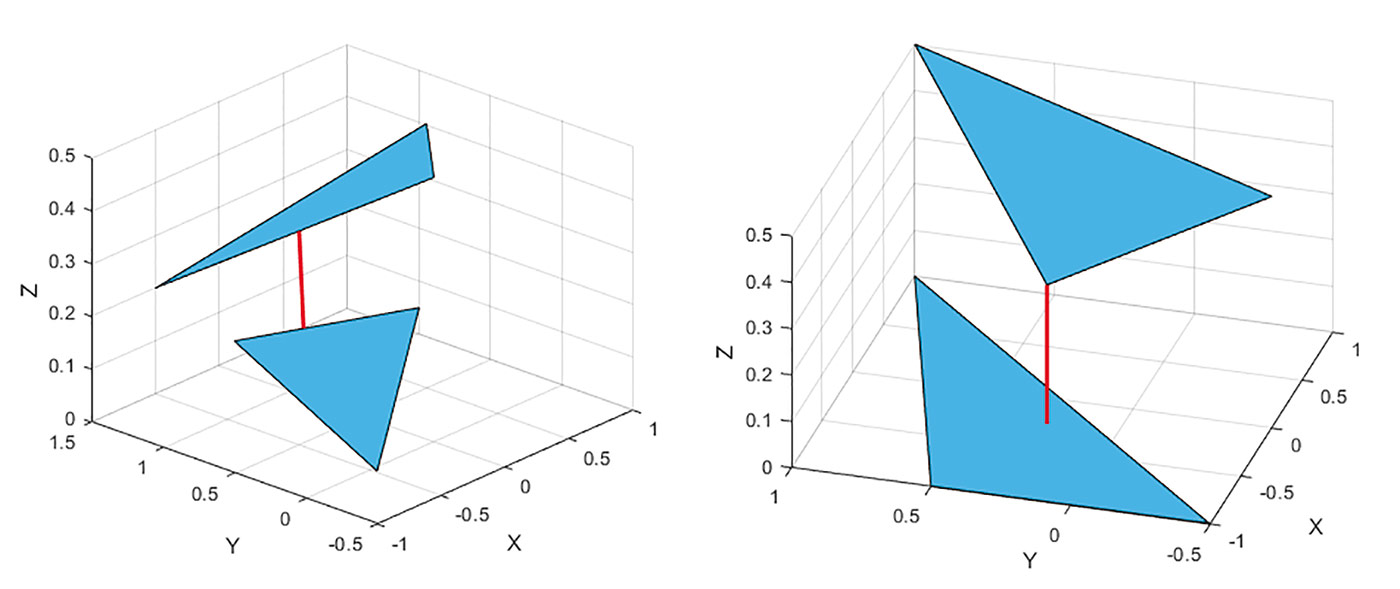
Рис. 1. Результат работы алгоритма поиска наименьшего расстояния между двумя плоскими треугольниками для двух общих случаев касания

Таким образом, для нахождения наименьшего расстояния между подобными твердыми телами нам ничего не остается, кроме как провести общий алгоритм нахождения ближайших точек плоских треугольников относительно всех треугольников, из которых состоят рассматриваемые твердые тела, и выбрать самое минимальное расстояние из найденных. Это и будет наименьшим расстоянием между двумя телами, обладающими триангулированной (произвольной) поверхностью.

Алгоритм определения столкновений нескольких твердых тел с триангулированной поверхностью

В качестве алгоритма обработки столкновений массива твердых тел было предложено разработать систему очередей, которая будет реализовываться внутри основного шага по сетке времени. Такой подход обоснован требованиями к высокой точности определения столкновений и к правильности обработки возможных случаев нескольких столкновений тел за один общий шаг по времени. Основной мерой близости тел, а в действительности мерой, по которой можно было бы определить, столкнулись ли рассматриваемые тела, является пересчитываемая на каждом шаге по времени скорость сближения тел. Этот параметр при достаточно мелком основном шаге по времени явялется наиболее доступным для расчета и применения критерием близости тел. Скорость сближения тел рассчитывается по найденным расстояниям на предыдущем и настоящем шаге.

Перейдем к описанию алгоритма реализации системы очередей для обработки столкновений массива твердых тел:

1 Создается очередь на текущем моменте времени t, представляющая собой вектор кортежей, содержащих всю необходимую информацию о близости всех тел.

2 Очередь фильтруется по потенциальным столкновениям за общий шаг по сетке времени. В результате такой проверки все пары тел, которые не столкнутся за настоящий шаг по времени t, покидают очередь.

3 Если очередь не пуста, то происходит сортировка очереди по времени возможного столкновения. Таким образом, самое ближайшее из возможных столкновений становится первым в очереди.

4 Если размер очереди равен нулю либо разность остатка по времени и времени ближайшего столкновения меньше нуля, то осуществляется переход к п. 5. В противном случае реализуются следующие действия:

а) происходит обработка столкновения тел, находящихся первыми в очереди. Если ближайших столкновений несколько (подшаг по времени, за который они произойдут, одинаков), то расчет происходит для всех этих тел;

б)     все тела совершают подшаг на промежуток времени, за который должно было произойти столкновение, деленный на некоторое постоянное натуральное число (не ноль), вынесенное в качестве входного параметра настоящего расчета. Из остатка по времени вычитается промежуток, на который тела совершили подшаг;

в) происходит возвращение к п. 1;

г) происходит возвращение к п. 2, только в качестве рассматриваемого промежутка времени берется остаток;

д)     происходит возвращение к п. 3.

5 Необходимо совершить подшаг всеми телами на промежуток времени, равный вычисленному остатку.

Следует также отметить, что в данной статье «шаг» по времени рассматривается как шаг расчета FlowVision (то есть шаг по времени с обновлением аэрогидродинамических сил на всех телах, принимающих участие в расчете), а «подшаг» по времени является шагом по времени алгоритма определения столкновений (системы очередей), то есть при работе системы очередей внутри основного шага FlowVision по времени считается, что тела находятся в постоянном поле сил.

Критериальное оценивание параллельности граней и ребер при столкновении

Во время различных тестов алгоритма было обнаружено несколько проблем, которые можно разделить на два общих случая: когда столкновение происходит при практически параллельных плоскостях сталкивающихся тел и когда столкновение происходит при практически параллельном ребре одного тела к плоскости другого.

Дело в том, что в первом случае реальное столкновение происходит в наиболее удаленной точке относительно центра масс каждого из тел (пусть эта точка принадлежит некоторой грани α1 одного тела и грани α2 другого тела), а следовательно, на телах возникает достаточно сильный угловой момент, вследствие которого тела обретают высокие противоположные по знаку угловые скорости и с большой вероятностью снова столкнутся, только в абсолютно другой точке на тех же гранях α1 и α2. Аналогичная ситуация происходит и во втором описанном ранее случае, только для ребра одного тела и грани другого тела.

Суть проблемы заключается в том, что в рассматриваемых случаях алгоритм определения столкновений плохо работает из-за требования к правильной обработке им в какой-то степени непредсказуемого общего шага дискретизации расчета по времени, а также из-за собственной малости промежутка времени между двумя вышеописанными столкновениями.

В качестве решения такой проблемы было предложено ввести критериальное оценивание параллельности ближайших граней двух тел и параллельности ближайшей грани одного тела к ребру другого в момент столкновения. Если считается, что грань или ребро одного тела параллельно грани другого, то столкновение происходит без вращения, иными словами, энергия столкновения переходит только в поступательные характеристики движения. Определиться с методом оценивания параллельности достаточно легко: необходимо лишь оценить углы между нормалями плоскостей ближайших граней двух тел в первом случае и между нормалью плоскости одного тела и ребром другого во втором, а затем сравнить, например, модуль косинуса такого угла с единицей и нулем в первом и втором случаях соответственно.

Однако ближайшие точки между двумя телами достаточно часто будут находиться в вершинах или на ребрах рассматриваемых тел, а значит, необходимо однозначно определять ближайшие грани между двумя телами. Самым очевидным решением в данном случае будет сравнение косинусов углов нормалей всех граней, содержащих ближайшую точку, и вектора, соединяющего ближайшую точку на рассматриваемом теле с ближайшей точкой на другом теле.

Учет пересечений и блокировок подвижных тел произвольной формы

При работе вышеописанного алгоритма с заданными критериями параллельности граней и ребер при адекватно заданном шаге по времени пересечение тел произвольной формы, как правило, может возникнуть в двух случаях: если неверно заданы критерии паралелльности либо если в процессе расчета возникли эксклюзивные ситуации, когда тело попало в так называемую блокировку. Блокировкой в данном случае считается неизбежность возникновения пересечения с дальнейшей невозможностью выхода из него тела при совокупности постоянного соударения с каким-либо другим телом и направлений результирующих аэрогидродинамических сил и моментов. Например, такая ситуация может возникнуть, когда положение тела «удерживается» средой (например, тело держится на поверхности воды), при этом другое, более массивное подвижное тело «проталкивет» его в третье, закрепленное (то есть неподвижное) тело; в таком случае пересечение рассматриваемых тел в рамках обсуждаемого алгоритма является неизбежным (рис. 2).

Рис. 2. «Идеальное» условие возникновения блокировки. У всех тел отключена угловая скорость и поступательная скорость по оси Z. Пусть левое тело «не реагирует» на столкновения с остальными телами. Справа показан результат обработки такой блокировки

Для обработки таких ситуаций вместе с поиском расстояний между плоскими треугольниками в евклидовом пространстве можно также реализовать и поиск пересечений таких треугольников. Для этого можно реализовать алгоритм, аналогичный алгоритму, представленному в [4]. Основная идея алгоритма заключается в нахождении линии пересечения плоскостей, содержащих треугольники, с дальнейшим поиском пересечений треугольников с этой линией. Работа такого алгоритма представлена на рис. 3.

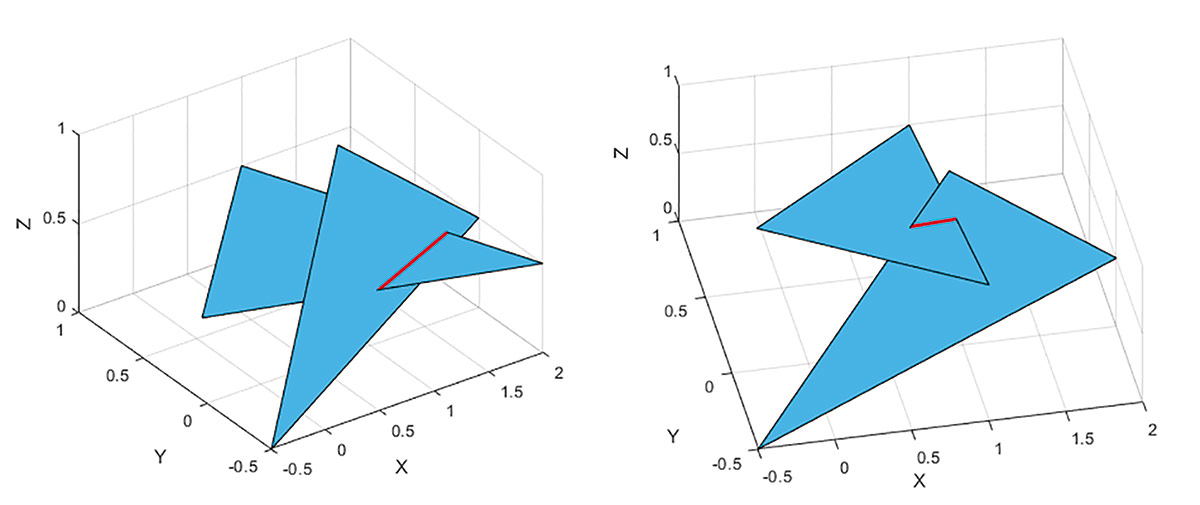
Рис. 3. Результат работы алгоритма поиска пересечений между двумя плоскими треугольниками для двух общих случаев касания

Если пересечение между двумя телами было найдено, то эта пара тел посылается в очередь обработки столкновений с нулевым расстоянием между ними (то есть они сразу считаются столкнувшимися), ненулевой скоростью сближения и информацией о ближайших точках с последнего шага (подшага) до пересечения. Дальнейший подшаг после обработки столкновения в системе очередей в таком случае можно оценивать по оставшемуся времени до конца шага (то есть до обновления аэрогидродинамических сил), исключив из обработки системой очередей этой пары тел до тех пор, пока в очереди не окажутся пары без пересечений или пока алгоритм системы очередей не завершится на текущем общем шаге.

Важной характеристикой пересечения является глубина проникновения одного тела в другое. Глубина проникновения может быть найдена, исходя из общих случаев касания треугольников, приведенных ранее. Так, для случая «вершина в грань» достаточно проверить все вершины каждого из треугольников на нахождение внутри одного из тел (алгоритм является стандартным в сфере 3D-моделирования), а затем найти грань, через которую было осуществлено проникновение, проведя луч из точки внутри тела по вектору, соединяющему ближайшие точки рассматриваемых тел до обнаружения пересечения. Далее необходимо лишь найти расстояние от точки внутри тела до плоскости найденной грани, через которую, предположительно, было осуществлено проникновение. Для второго случая — «ребро в ребро» — достаточно провести поиск ближайших точек между всеми отрезками двух треугольников (в итоге получим девять расстояний и девять пар ближайших точек) и проверить каждую пару ближайших точек на нахождение внутри соответствующих тел. Если совпадение при подобной проверке не было найдено (такое возможно при слишком малых пересечениях), то величина проникновения определяется по минимальному значению, которое может меняться в зависимости от задачи.

«Лечение» возникающих в ходе расчета блокировок может быть реализовано достаточно просто: при обнаружении подряд двух и более пересечений рассматриваемого тела с другим и выполнении условия положительности проекции разности скоростей последних ближайших найденных точек между этими телами (в таком случае считается, что тела сближаются, а не выходят из пересечения), линейный размер тела уменьшается таким образом, чтобы тело вышло из «удвоенного» пересечения (то есть «с запасом»). Уменьшение подразумевает операцию масштабирования отсносительно некоторой точки (удобнее всего брать центр масс тела). Аргументом масштабирования является величина, на которую умножаются линейные размеры тела. Так как масса пропорциональна объему, то при масштабировании она будет изменяться в кубе от аргумента, а тензор инерции рассматриваемого тела — в пятой степени от аргумента масштабирования.

Уменьшение размера тела соответствует его физическому истиранию (разрушению), что вполне применимо для задач движения судна по битому льду и для других задач, где возможно истирание поверхности тела.

При наличии большого массива однородных тел их гораздо удобнее обрабатывать как одно целое подвижное несвязное тело, собирая такой массив в один общий регион обмена геометрией для дальнейшей передачи в CAE-пакет FlowVision. При этом солвер FlowVision запрещает возникновение самопересечений в рамках одного региона обмена геометрией. Эту проблему возможно обойти с помощью введения каркасов (рис. 2 и 4) для всех тел, составляющих регион обмена геометрией, и в дальнейшем обрабатывать столкновения слегка увеличенных в объеме дубликатов этих тел. При этом проводить обмен с FlowVision можно с помощью находящихся как бы внутри этих каркасов основных моделируемых тел.

Рис. 4. Визуализация возникающего обрабатываемого пересечения каркасов тел (полупрозрачный белый), содержащих основные тела расчета FlowVision (голубой)

Примеры применения разработанного алгоритма

Ниже приведено несколько основных примеров, на которых тестировались вышеописанные процедуры обработки движения и столкновений тел, а также процедура определения столкновений.

Модификация алгоритма для известных тел, состоящих из аналитических поверхностей

Зачастую тела в задачах, требующих введения алгоритма определения столкновений, можно обобщить на известные тела (например, сферы, цилиндры, прямоугольники и т.д.) с известным набором аналитических (то есть плоских, сферических, цилиндрических и т.д.) поверхностей. В таком случае для поиска наименьших расстояний между телами вместо обхода всех их фасетчатых поверхностей можно применить средства аналитической геометрии, то есть использовать отдельный частный быстрый алгоритм поиска наименьшего расстояния для каждой из возможных пар рассматриваемых известных тел. При расчете скорости сближения тела автоматически будут считаться столкнувшимися в случае обнаружения какого-либо их пересечения (при рассмотрении тел, поверхность которых состоит из аналитических поверхностей, обнаружение их пересечения является достаточно простой задачей). Таким образом, будет получен следующий алгоритм обнаружения столкновений:

1 Создается очередь на текущем моменте времени, представляющая собой вектор кортежей, содержащих всю необходимую информацию о близости всех тел, принимающих участие в расчете, без повторений.

2 Очередь фильтруется по потенциальным столкновениям за общий шаг по времени. Пары тел, не прошедшие проверку, покидают очередь.

3 Если очередь не пуста, то происходит сортировка очереди по времени возможного столкновения. Если после прохождения п. 2 тела в настоящей очереди считаются пересеченными, то время столкновения считается равным нулю, то есть пары пересекающихся тел автоматически попадают в начало очереди.

4 Пока размер очереди не равен нулю, реализуется следующий цикл:

а) происходит обработка столкновений тел, находящихся первыми в очереди. Если ближайших столкновений несколько (промежуток времени, за который они произойдут, одинаков), то расчет совершается для всех этих тел;

б) происходит возвращение к п. 1;

в) происходит возвращение к п. 2; в расчет не берутся последние из столкнувшихся пар тел. Промежуток времени, по которому фильтруется очередь, не изменяется, то есть столкновения снова ищутся за общий шаг по времени, пришедший с FlowVision;

г) происходит возвращение к п. 3.

Если очередь пуста, то необходимо «шагнуть» всеми телами на основной промежуток времени, пришедший с FlowVision.

Таким образом, был получен алгоритм определения столкновений для тел с аналитическими поверхностями, не требующий совершения подшагов внутри основного шага по времени. Кроме того, подобный алгоритм более требователен к шагу по сетке времени.

Пример эволюции расчета для задачи моделирования множественных столкновений сферических тел с внутренней стенкой неподвижной трубы представлен на рис. 5. Труба имеет длину 90 мм, внутренний радиус порядка 21 мм, а каждое из сферических тел имеет радиус около 2 мм. Масса трубы при этом равна 340 г, а масса каждого из сферических тел — 0,38 г. Труба считается закрепленным неподвижным телом, линия ее цилиндрической симметрии параллельна оси OY. Количество тел сферической формы равно 23, своим расположением они образуют «кольцо» внутри трубы. Все тела сферической формы имеют одинаковую координату по OY и некоторый вектор поступательной скорости в начальный момент времени. Расчет проводился в вакууме без сил гравитации.

Рис. 5. Эволюция расчета задачи моделирования множественных столкновений сферических тел с внутренней стенкой неподвижной трубы с шагом 0,25 с

Применение разработанного алгоритма в задаче моделирования столкновения льдин с корпусом судна

В качестве основного проекта для интегрирования алгоритма определения столкновений множества твердых тел, обладающих произвольной триангулированной поверхностью, в CAE-пакет FlowVision была рассмотрена задача моделирования столкновения множества льдин с корпусом судна в канале, ограничивающем их движение. Философия методики проведения расчета может быть описана следующим образом: в пользовательской программе реализуется расчет движения и столкновений тел. С помощью встроенного в FlowVision коннектора MBC пользовательская программа передает геометрию (с учетом движения и столкновений) всех тел, принимающих участие в аэрогидродинамическом расчете. Задача FlowVision — рассчитывать аэрогидродинамические силы на твердых телах, интерполировать их в вершины рассматриваемых тел и передавать эти силы с помощью коннектора MBC в программу вычисления перемещений. Следует напомнить, что шаг расчета по времени и условия на границах рассматриваемых тел определяются внутри FlowVision.

Рассмотрим основные параметры модельной задачи: будем считать, что в задаче присутствует земная гравитация, а также жидкая вода в отрицательной части оси OZ и вакуум в положительной части оси OZ. Таким образом, в начальный момент времени граница «вода — вакуум» находится во всем пространстве расчета при z = 0. Пусть льдины — равнобедренные треугольные призмы (каждая массой 0,5 кг), расположенные в начальный момент времени так, как показано на рис. 6, корпус судна — сложное тело массой 125 кг, а берега имеют сложную форму вблизи начального положения льдин. Тензоры инерции для каждого из тел вычисляются по их линейным размерам для известных фигур: для корпуса судна можно взять приближение растянутого полудиска, а для берегов — прямоугольного параллелепипеда. Все следующие рисунки показаны для каркасов обрабатываемых во FlowVision тел (корпус судна также обладает каркасом упрощенной формы, однако для него отключена функция масштабирования при возникновении блокировки). Результаты моделирования представлены на рис. 7-9.

Рис. 6. Начальное положение тел в рассматриваемой задаче моделирования столкновения льдин с корпусом судна

Рис. 7. Результат моделирования 6 с расчета столкновений массива льдин с корпусом судна в канале

Рис. 8. Эволюция моделирования задачи расталкивания льдин корпусом судна в свободной воде с шагом 0,5 с

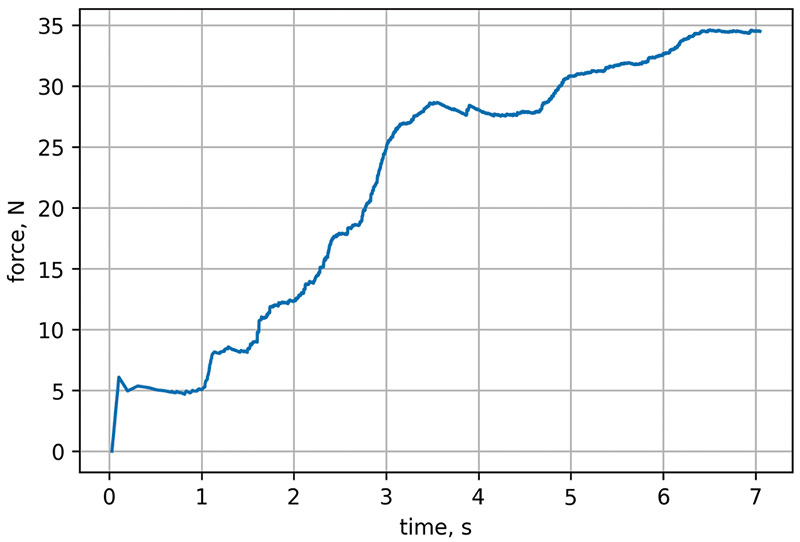
Рис. 9. Зависимость сопротивления льда на корпусе судна от времени расчета

Итоги

В настоящей работе рассмотрено столкновение твердых тел произвольной формы во время аэрогидродинамического расчета. В качестве основного отладочного проекта был реализован расчет движения и столкновений битого льда в канале с корпусом судна. Был получен достаточно быстрый и точный метод определния столкновения твердых тел. Практика применения разработанного алгоритма как отдельно, так и вместе с аэрогидродинамическим расчетом в CAE-пакете FlowVision показывает, что он способен справляться с задачами научного и инженерного моделирования, где требуется одновременное выполнение уравнений гидродинамики и механики движения твердых тел.

Литература:

1. Лившиц Е.М., Ландау Л.Д. Теоретическая физика. Том 1. Механика, 4-е изд., испр. М.: Наука. Гл. ред. физ.-мат. лит., 1988, с. 126-168.
2. Шарипов Р.А. Курс аналитической геометрии: Учебное пособие, РИЦ БашГУ, 2010.
3. Vladimir J. Lumelsky, On fast computation of distance between line segments, Inform. Proc. Lett. v.21, p.55-61, 1985.
4. Tomas Akenine-Möller, A Fast Triangle-Triangle Intersection Test, J. Graphics, GPU, & Game Tools 2, p.25-30, 1997.