Анатолий Донецков,
к.т.н., доцент кафедры информатики и информационных технологий Калужского государственного университета им. К.Э. Циолковского
Статья содержит описание программного обес-печения «Модель», которое позволяет проводить анализ систем различного назначения с помощью сетей Петри.
Сети Петри являются популярным инструментом моделирования и исследования систем различного назначения [1, 2]. Автором было разработано программное обеспечение моделирования и анализа систем с помощью сетей Петри, получившее условное наименование «Модель». Программное обеспечение (ПО) разработано на языке VBA в среде MS Excel. ПО «Модель» позволяет проводить анализ сети, используя матричное представление сетей Петри:
C =
где P — множество позиций {p1, p2, … pm}; T — множество переходов {t1, t2, … tm}; D+ — выходная матрица; D- — входная матрица [3].
Файл Excel (xlsm) представляет собой сжатый zip-файл, структура которого показана на рис. 1.
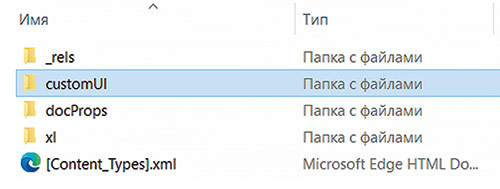
Рис. 1. Структура файла xlsm (zip)
В папке customUI создаем xlm-файл customUI14.xml (рис. 2), который будет содержать меню ПО «Модель» (рис. 3).
Рис. 2. Фрагмент содержимого файла customUI14.xml
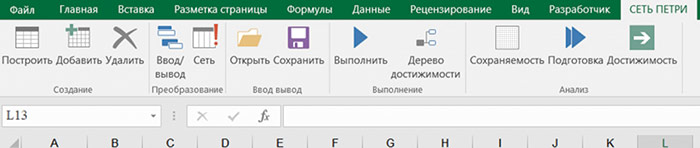
Рис. 3. Меню программы «Модель»
Рассмотрим работу ПО «Модель» на классическом примере — рис. 4 [2].
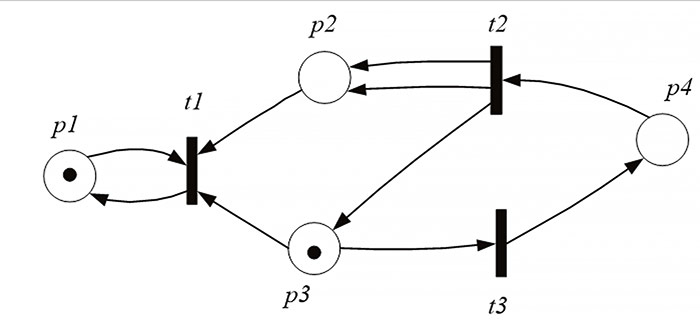
Рис. 4. Сеть Петри
Выполняем команду Построить (рис. 5). Команда создает заготовку для ввода информации о сети Петри.
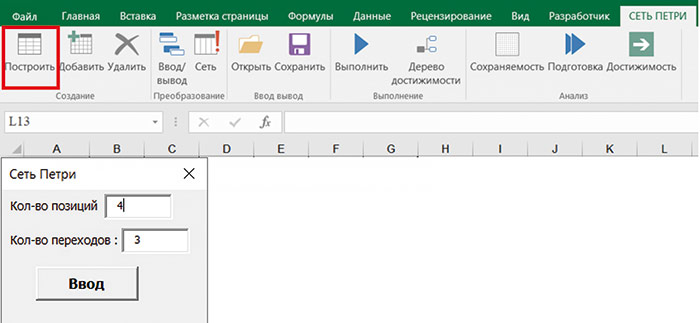
Рис. 5. Создание новой сети Петри
Вводим информацию о сети на листах: сеть, маркировка, вход_выход (рис. 6).
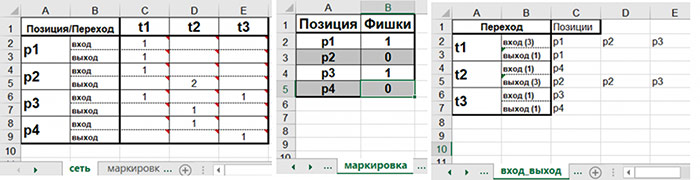
Рис. 6. Ввод информации о сети Петри
Команда Выполнить позволяет выполнять сеть Петри: осуществлять запуск перехода и возвращаться назад, то есть проходить по пространству состояний введенной сети Петри R=
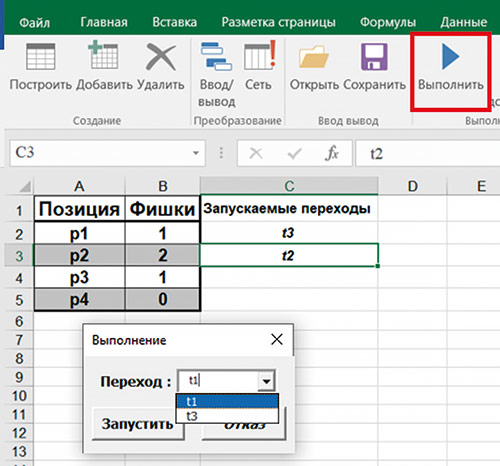
Рис. 7. Запуск перехода
В поле Переход (рис. 7) виден список разрешенных переходов в данной маркировке.
Программный комплекс «Модель» позволяет решать задачи анализа: построение дерева достижимости, сохранения и достижимости.
Команда Дерево достижимости позволяет строить дерево достижимости введенной сети Петри (рис. 8).
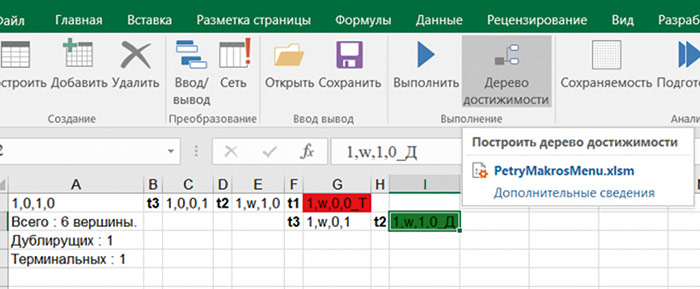
Рис. 8. Дерево достижимости
В ячейке A1 начальная маркировка, в колонках B, D и т.д. через один расположены наименования запускаемых переходов, а в колонках C, E и т.д. через один расположены маркировки, которые получаются в результате запуска перехода. Дополнительно на листе диаграммы создается диаграмма распределения вершин в дереве достижимости (рис. 9).
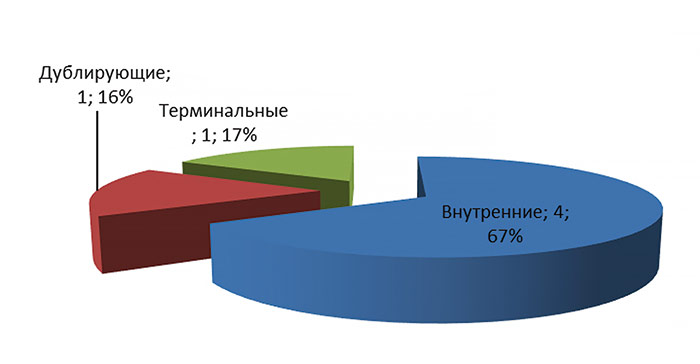
Рис. 9. Диаграмма распределения вершин
Программа «Модель» позволяет решать задачу анализа сохранямости с помощью команды Сохраняемость, используя встроенный пакет Solver (рис. 10).
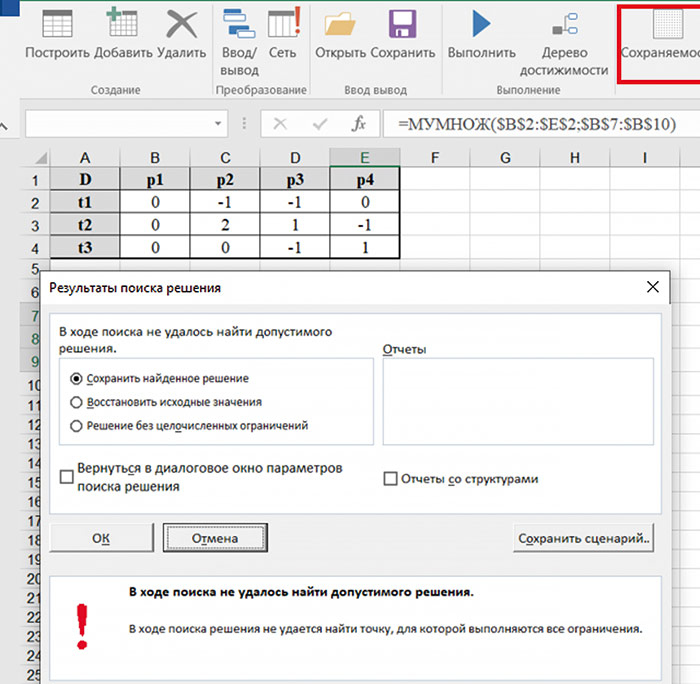
Рис. 10. Решение задачи сохраняемости
Следовательно, введенная сеть Петри (см. рис. 4) не сохраняет ресурсы.
Программное обеспечение, разработанное автором, позволяет решать задачу достижимости. Рассмотрим на следующем примере: достижима ли маркировка (1, 8, 0, 1) из начальной маркировки (рис. 11).
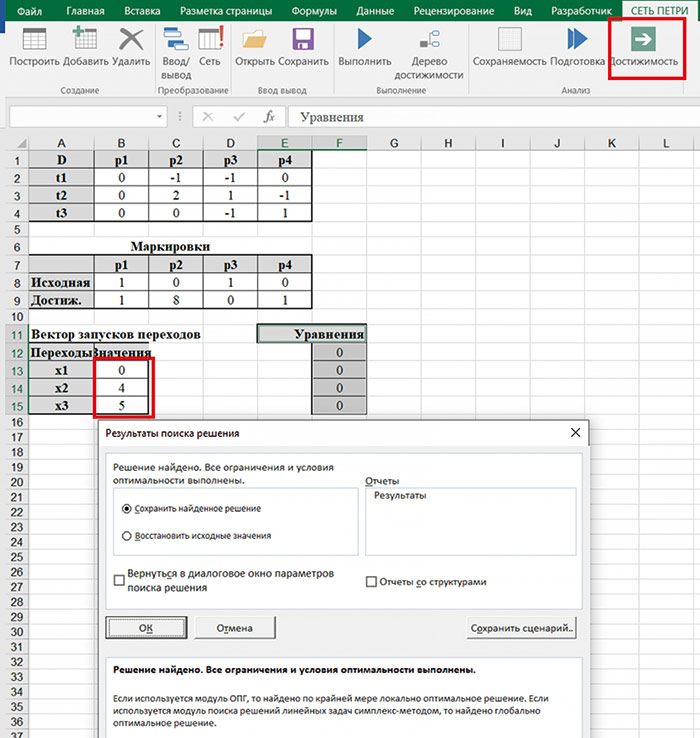
Рис. 11. Решение задачи достижимости
В результате выполнения команды Достижимость (см. рис. 11) было найдено следующее решение: запустив переход t2 4 раза, а переход t3 — 5 раз, маркировка (1, 8, 0, 1) может быть достижима. Решим следующую задачу, достижима ли маркировка (1, 4, 0, 2) — рис. 12.
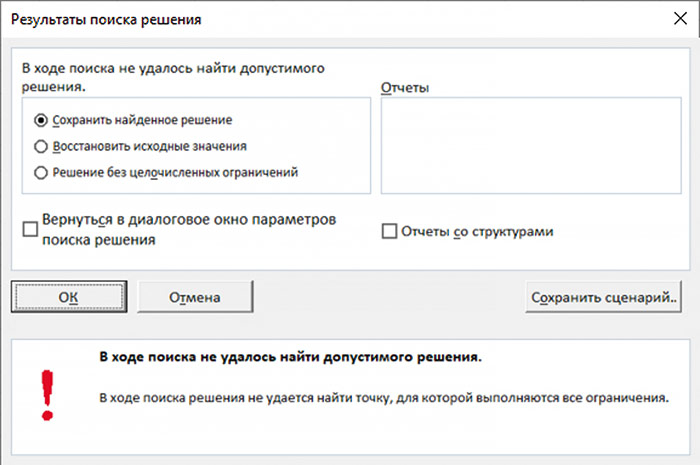
Рис. 12. Решение задачи достижимости маркировки (1, 4, 0, 2)
В результате оказалось, что маркировка (1, 4, 0, 2) не достижима из маркировки (1, 0, 1, 0).
ПО «Модель» успешно используется в учебном процессе КГУ имени К.Э. Циолковского.
Список литературы:
- Лескин А.А., Мальцев П.А., Спиридонов А.М. Сети Петри в моделировании и управлении. Л.: Наука, 1989. С. 133.
- Питерсон Дж. Теория сетей Петри и моделирование систем. М.: Мир, 1984. С. 264.
- Анализ сетей Петри на основе матричных уравнений [Электронный ресурс]: https://cyberpedia.su/21x3e5c.html (дата обращения: 4.11.2024).
