Решение нестандартных задач графической параметризации объектов в nanoCAD BIM Строительство

Олег Ачкасов,
инженер ООО «Макссофт-24»

Пользователи BIM-решения для архитекторов и конструкторов nanoCAD BIM Строительство, конфигурация «Конструкции» (ранее — nanoCAD BIM Конструкции), сталкиваются с задачами параметризации графики объектов. Многие задачи можно решать, не углубляясь в возможности параметризации, но нередко возникают ситуации, когда необходимо задать сложные геометрические зависимости. И в этих случаях у пользователей возникает множество вопросов.

Как правило, имеющиеся учебные и справочные материалы подразумевают базовое знакомство с функционалом параметризации графики объектов. Из имеющихся описаний функционала не всегда очевидно, как можно прийти к тому или иному решению, так как в справочных материалах нет подробного анализа применения функций для решения задач параметризации объектов. Разбор примеров сложной параметризации может позволить пользователю лучше понять, как и в рамках какой логики применяются функции параметризации. Эта статья написана в помощь пользователям, которые сталкиваются с ситуациями, когда к параметризации геометрии объекта предъявляются сложные и нетривиальные требования. Очевидно, что разобрать все возможные варианты в рамках одной статьи не представляется возможным. Однако в этой статье мы раскрываем принципы работы с векторами и точками при параметризации графики.

Для случаев, когда необходимо:

• параметризовать положение 3D-/2D-примитивов в Редакторе параметрического объекта;
• параметризовать точки контура в операции 3D-выдавливания в Редакторе параметрического объекта;
• задавать положение элементов объекта в пространстве, которое бы учитывало параметризацию поворотов относительно осей XYZ, уметь пользоваться функциями по работе с векторным типом данных и понимать, как именно и где задается соответствующая параметризация.

Параметризация положения 3D-/2D-примитивов

Начнем с рассмотрения теории вопроса. Положение параметрического объекта в пространстве модели задается относительно мировой системы координат, а положение геометрических примитивов объекта задается относительно локальной системы координат объекта. Начало локальной системы координат объекта соответствует точке его вставки. Эта система представлена на рис. 1.

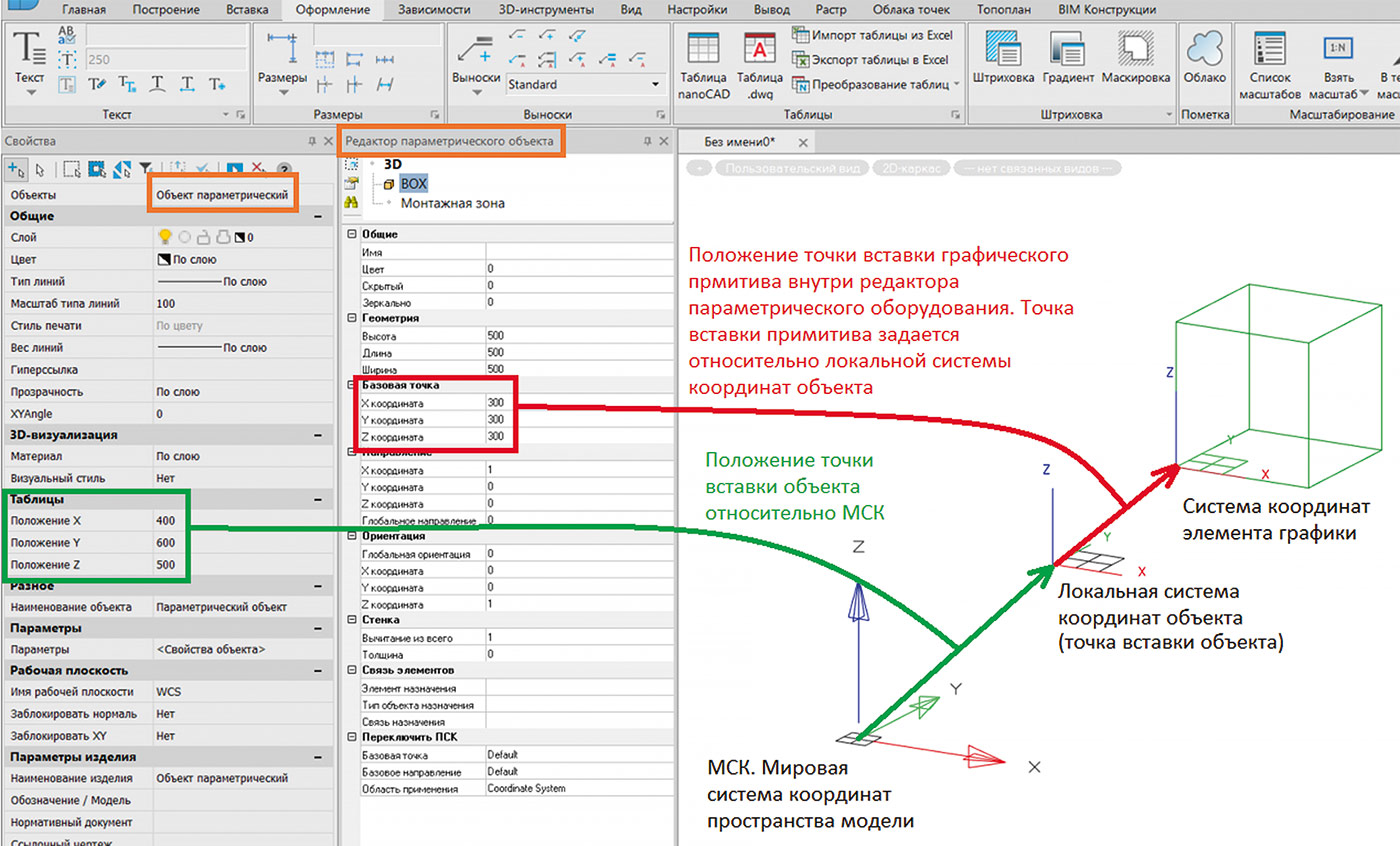
Рис. 1. Расположение систем координат объекта

По умолчанию у объектов категории параметрического оборудования есть три «ручки», которые позволяют задавать:

• поворот объекта относительно оси Z локальной системы координат. В момент активации «ручки» оси мировой системы координат встают туда же, где находится локальная система координат объекта (рис. 2);
• перемещение вдоль оси Z локальной системы координат объекта. При активации «ручки» ось X мировой системы координат встает вдоль оси Z локальной системы координат объекта (рис. 3);
• точку вставки объекта относительно мировой системы координат. При активации этой «ручки» мировая система координат остается на месте (рис. 4).

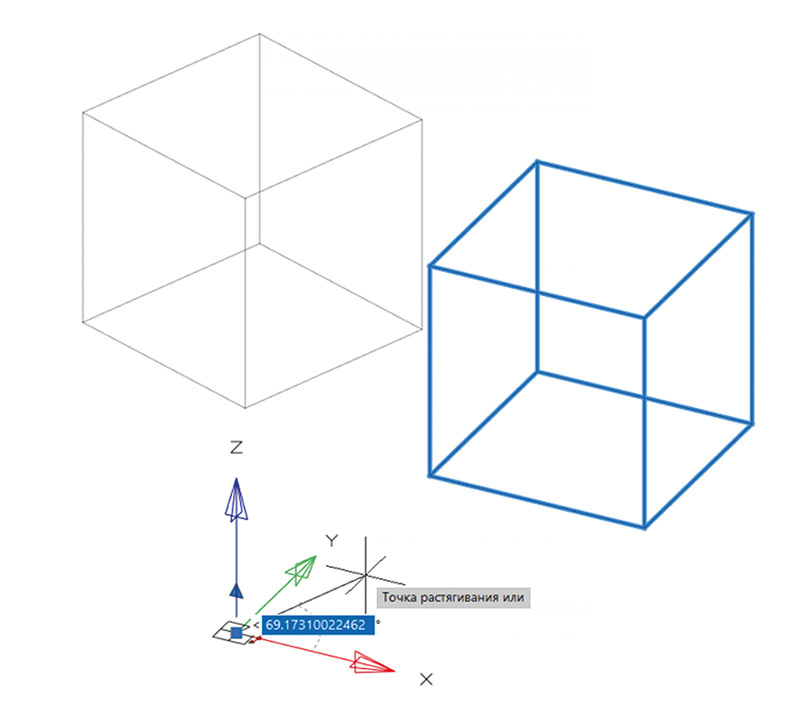
Рис. 2. Вращение объекта вокруг оси Z

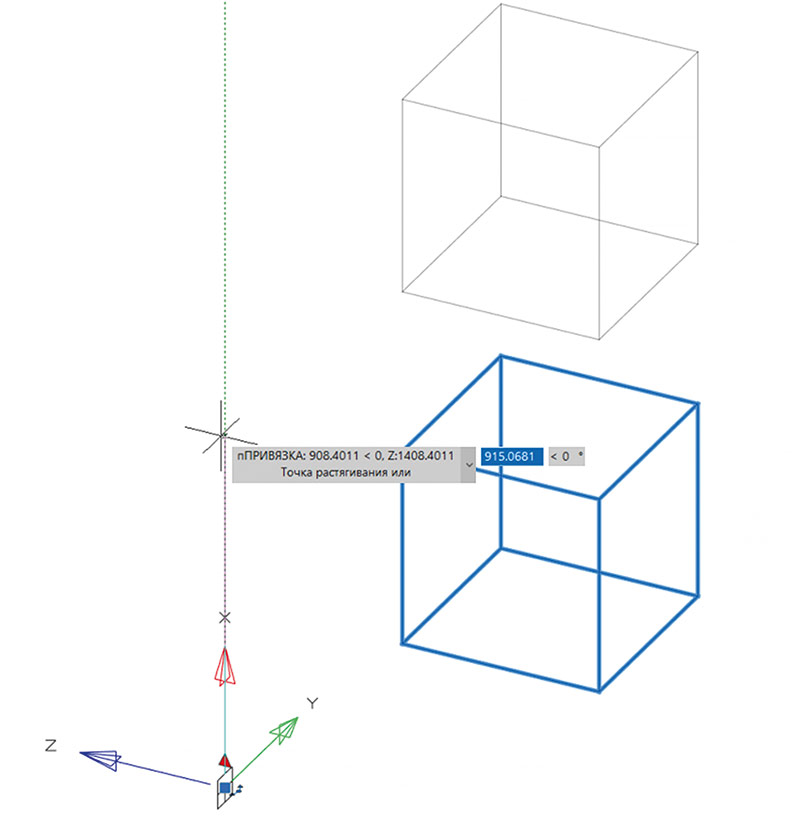
Рис. 3. Смещение объекта вдоль оси Z

Размещение объекта относительно мировой системы координат не ограничивается «ручкой» точки вставки объекта. Для размещения объекта доступны все имеющиеся в Платформе nanoCAD команды: ПЕРЕНЕСТИ, ПОВЕРНУТЬ, 3drotate и т.п. Но задание положения и ориентации элементов графики (примитивов объекта) необходимо параметризовать в Редакторе параметрического объекта. Разбору вариантов такой параметризации и посвящена статья.

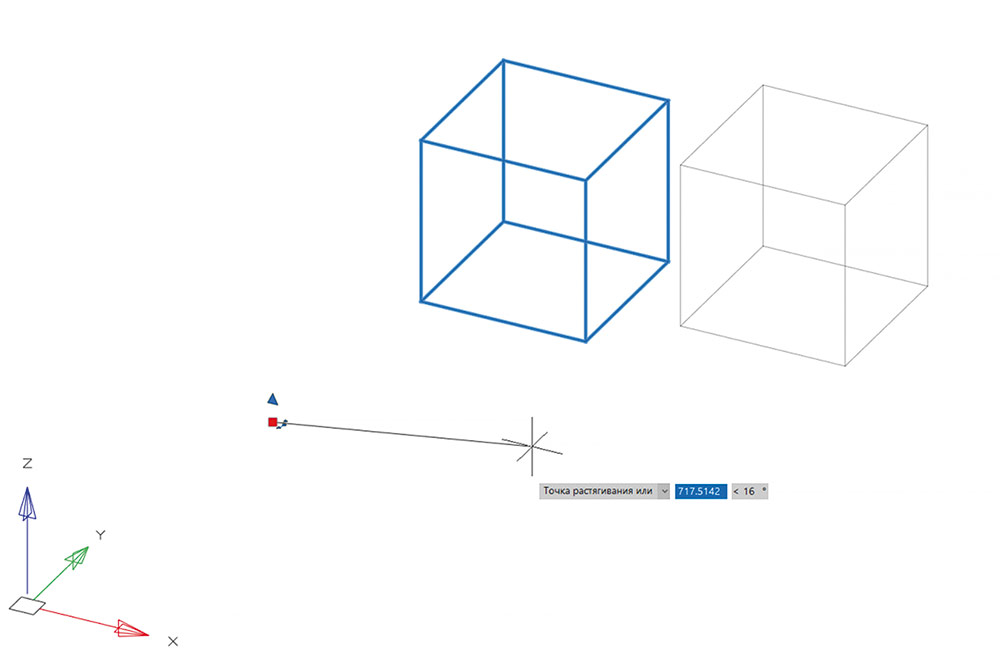
Рис. 4. Изменение точки вставки

Начнем с задания точки положения примитива объекта (рис. 5). Большая часть примитивов, которые можно добавить в Редактор параметрического объекта, обладает группой параметров базовой точки. Эта группа параметров позволяет задать положение примитива относительно локальной системы координат объекта либо относительно системы координат группы.

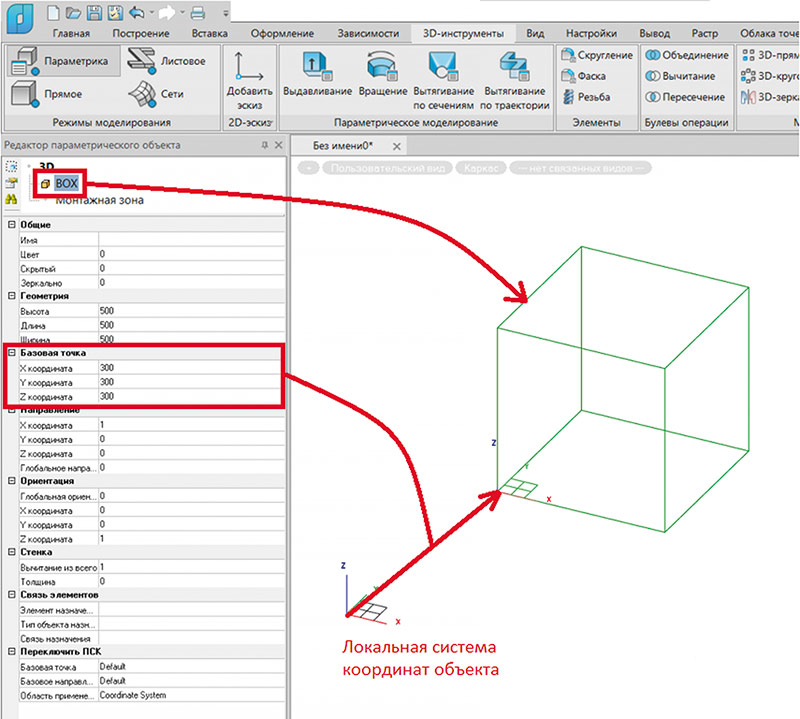
Рис. 5. Задание базовой точки примитива

Система координат группы также может иметь собственные координаты положения относительно локальной системы координат (рис. 6). Группы в Редакторе параметрического объекта позволяют задавать параметризацию некоторых параметров сразу для всех элементов, которые входят в группу. Кроме того, группы позволяют выполнять штриховку замкнутых контуров, объединение геометрии 3D-тел, находящихся внутри группы, назначение параметров по цвету и видимости сразу для всех элементов группы. И это далеко не все возможности этого структурного элемента.

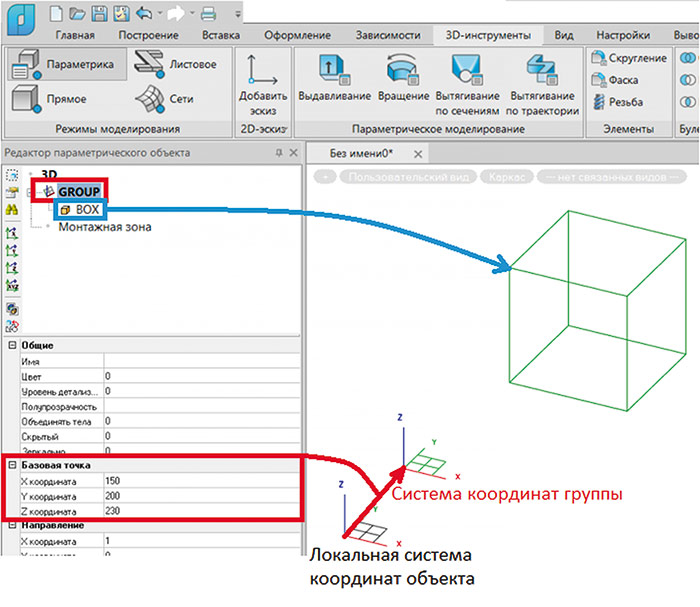
Рис. 6. Задание базовой точки группы

Примитивы, которые находятся в группе, определяют свое положение не от начала локальной системы координат объекта, а от начала системы координат группы (рис. 7).

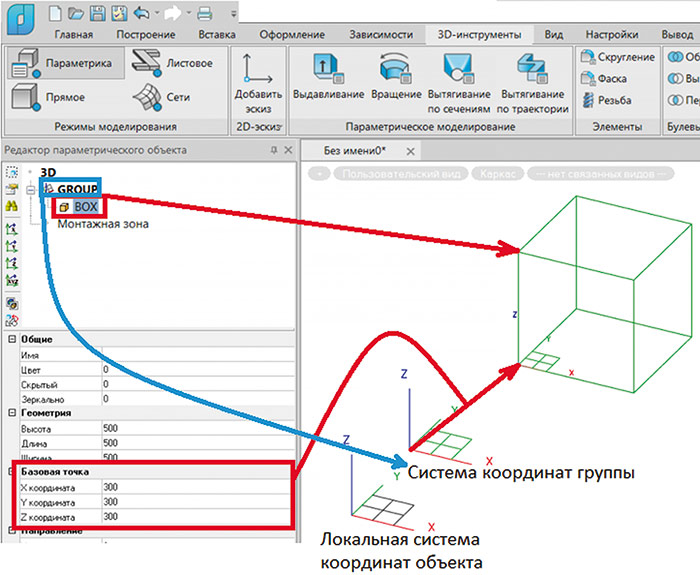
Рис. 7. Задание базовой точки относительно координат группы

Очевидно, что положение примитивов или групп примитивов задается тремя значениями координат XYZ. Все эти значения можно параметризовать. Для этого необходимо навести курсор на поле значения и нажать на троеточие (рис. 8).

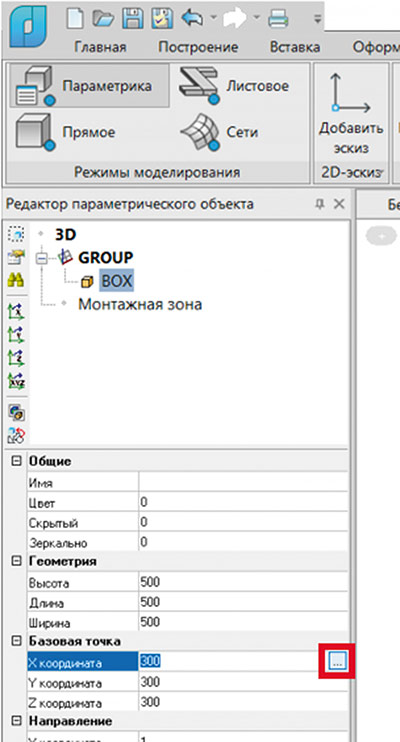
Рис. 8. Открытие окна Мастера функций для параметра

После этого откроется окно Мастера функций, в котором можно написать формулу для расчета значения параметра. Для расчета значения можно применить пользовательские переменные и параметры объекта. На рис. 9 представлен пример, демонстрирующий использование значения параметра объекта.

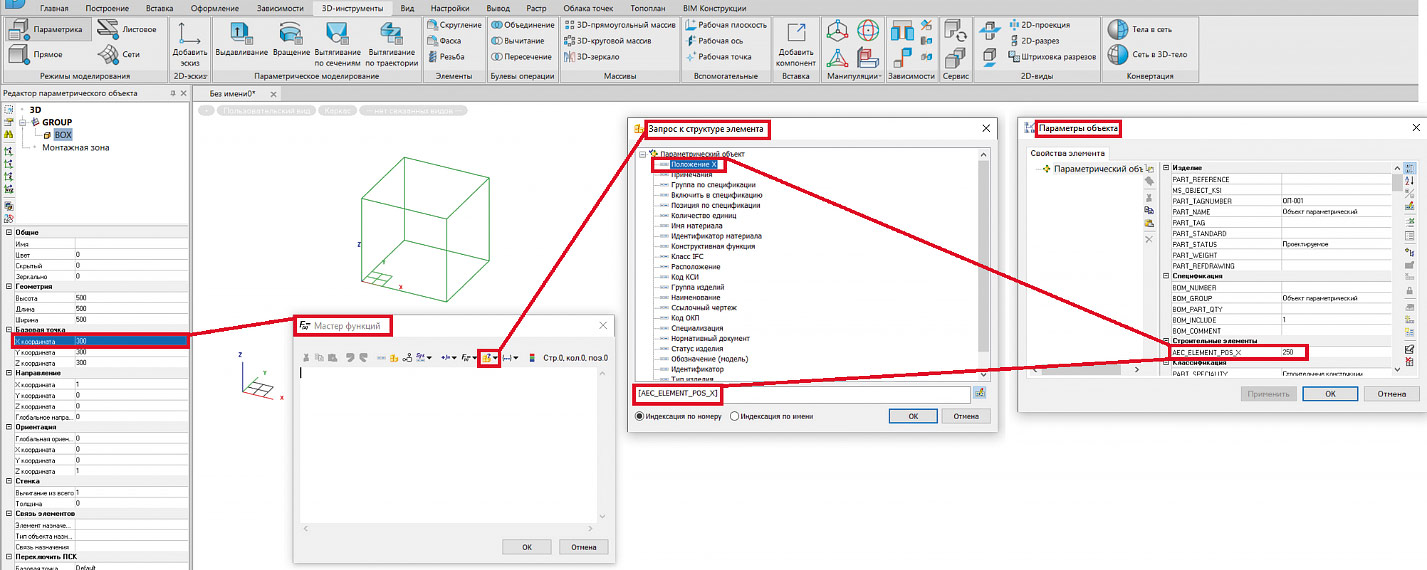
Рис. 9. Получение значения параметра по его имени

Имя параметра подставляет значение последнего. Это значение может участвовать в расчете формулы в случае применения различных операций: сложение, вычитание, умножение, деление, округление значения и т.п. На рис. 9 показана формула, которая берет значение параметра [AEC_ELEMENT_POS_X]. Значение параметра задано в окне параметров и равно 250. В формуле Мастера функций из этого значения вычитается 50. Таким образом, значение положения по оси X для примитива BOX становится равным 200. Напротив параметра, для которого задана формула, появляется значок f(x). Этот значок подсказывает пользователю, что значение является не статическим, а рассчитывается с помощью формулы (рис. 10).

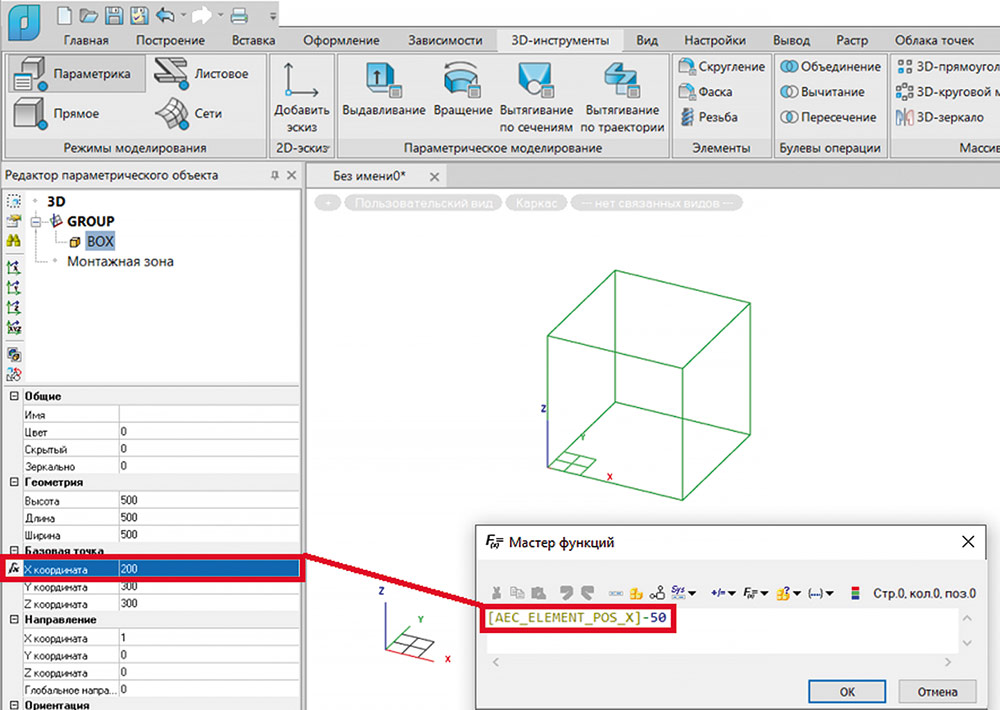
Рис. 10. Пример простой формулы по расчету координаты X базовой точки

При изменении параметра [AEC_ELEMENT_POS_X] в окне параметров объекта соответственно меняется значение параметра положения базовой точки по координате X для примитива BOX. [AEC_ELEMENT_POS_X] = 430.

[AEC_ELEMENT_POS_X] — 50 = 380 (рис. 11).

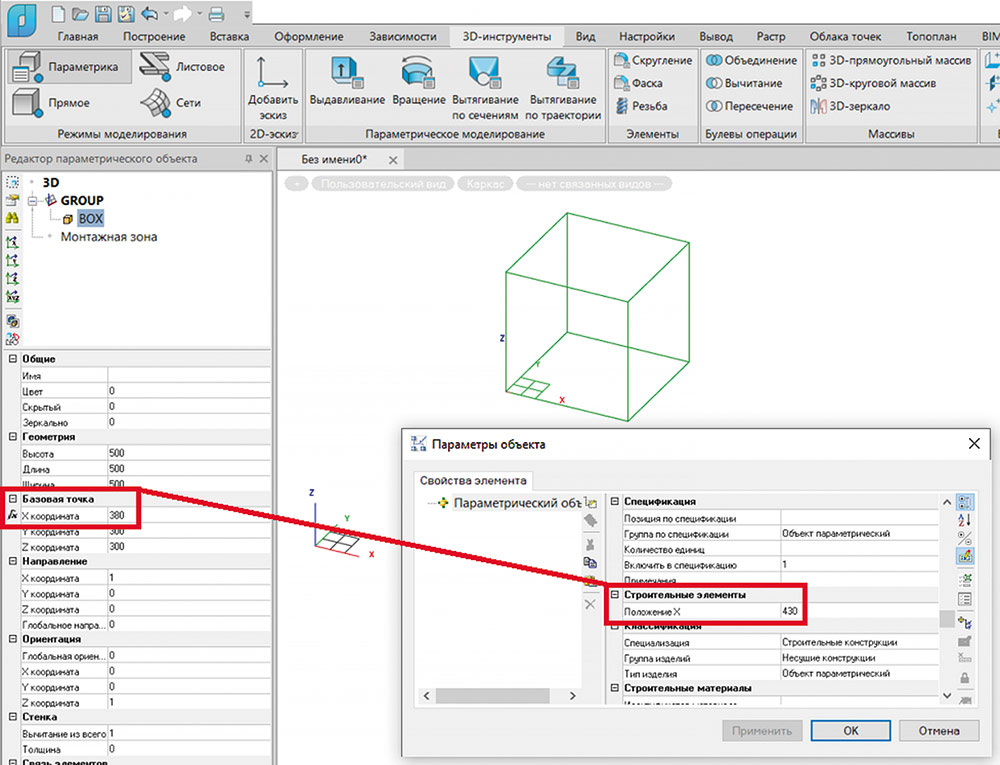
Рис. 11. Пример результата расчета

Таким образом пользователь может менять положение элементов графики параметрического объекта, задавая соответствующие значения и формулы. Но описанный выше способ не очень интерактивен, так как для изменения параметра необходимо открывать окно параметров объекта. Намного удобнее редактировать положение примитивов объекта, используя «ручки».

Рассмотрим параметризацию положения с использованием соответствующих «ручек». В окне Редактора параметрического объекта можно задавать множество «ручек» объекта. Чтобы добавить «ручку», необходимо в контекстном меню выбрать пункт Ручка. А далее указать, какую «ручку» вы хотите использовать (рис. 12).

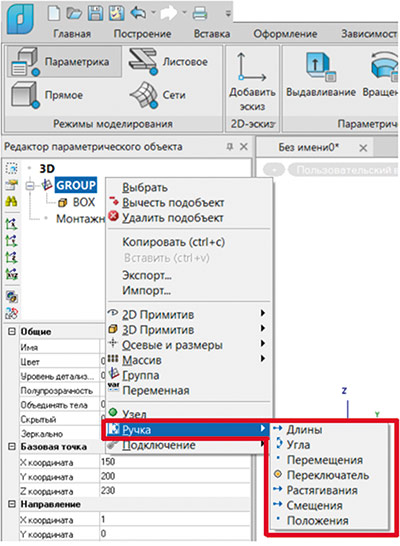
Рис. 12. Перечень «ручек» объектов

• «ручка» длины задает длину графических примитивов Редактора параметрического объекта. Ручка передает значение расстояния от своей базовой точки до положения «ручки»;
• «ручка» угла задает угол поворота графических примитивов. «Ручка» передает значение угла;
• «ручка» перемещения позволяет задавать положение всего объекта аналогично «ручке» вставки объекта. «Ручка» не передает никаких координат в свойства объекта;
• «ручка» переключателя позволяет интерактивно переключать значение параметров объекта;
• «ручка» растягивания позволяет задать размер объекта и угол поворота всего объекта. Угол поворота не передается в явном виде в отличие от «ручки» угла поворота;
• «ручка» смещения задает длину графических примитивов. «Ручка» передает значение расстояния от своей базовой точки до положения «ручки»;
• «ручка» положения передает значения своих координат относительно локальной системы координат объекта.

Наиболее универсальная из всех перечисленных «ручек» — «ручка» положения. При соответствующей параметризации она позволяет заменить все прочие «ручки», кроме «ручки» переключения. Универсальность достигается за счет того, что эта «ручка» передает значения координат своего положения. А зная координаты положения точек в пространстве, можно параметризовать всю необходимую геометрию. Также эта «ручка» позволяет задавать множество параметризации геометрии, которую не позволяют сделать другие «ручки».

Теперь применим на практике эти знания. Рассмотрим использование «ручки» для задания положения примитива объекта.

Создадим «ручку» положения (рис. 13).

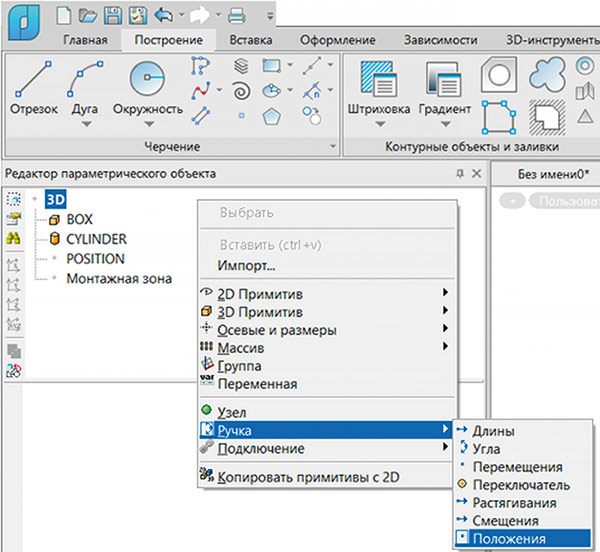
Рис. 13. Добавление «ручки» положения

В свойствах объекта создадим параметр Координаты ручки позиции. Необязательно использовать именно этот параметр, главное, чтобы у параметра был подходящий тип данных, например строковый. Но в этом случае заголовок параметра точно отображает назначение параметра (рис. 14).

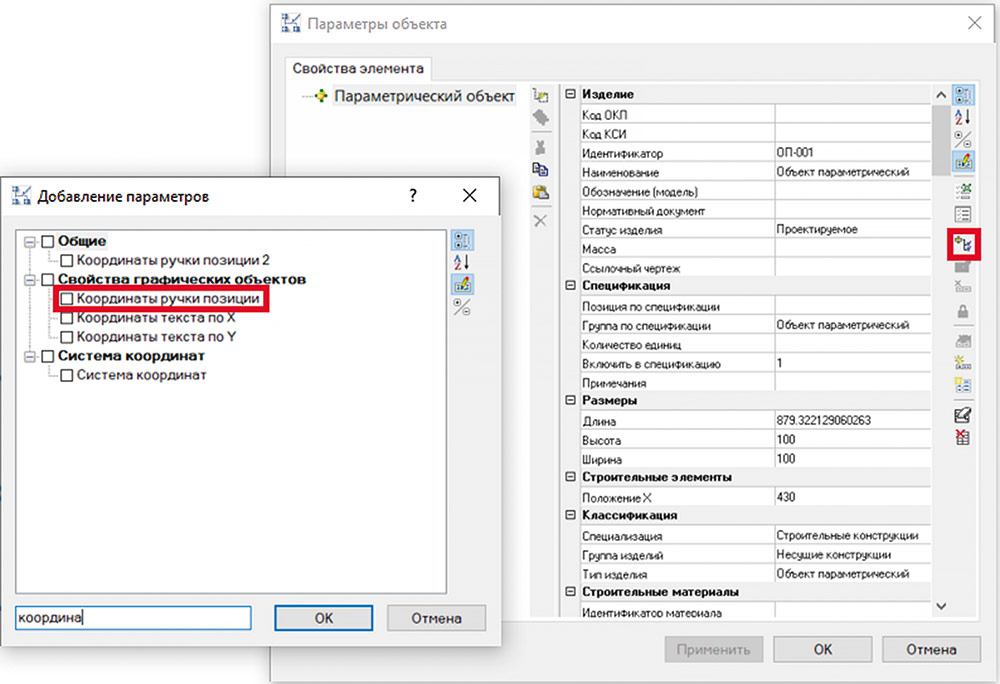
Рис. 14. Добавление параметра для координат «ручки» положения

В Редакторе параметрического объекта в параметре Назначение укажем добавленный параметр Координаты ручки положения (рис. 15).

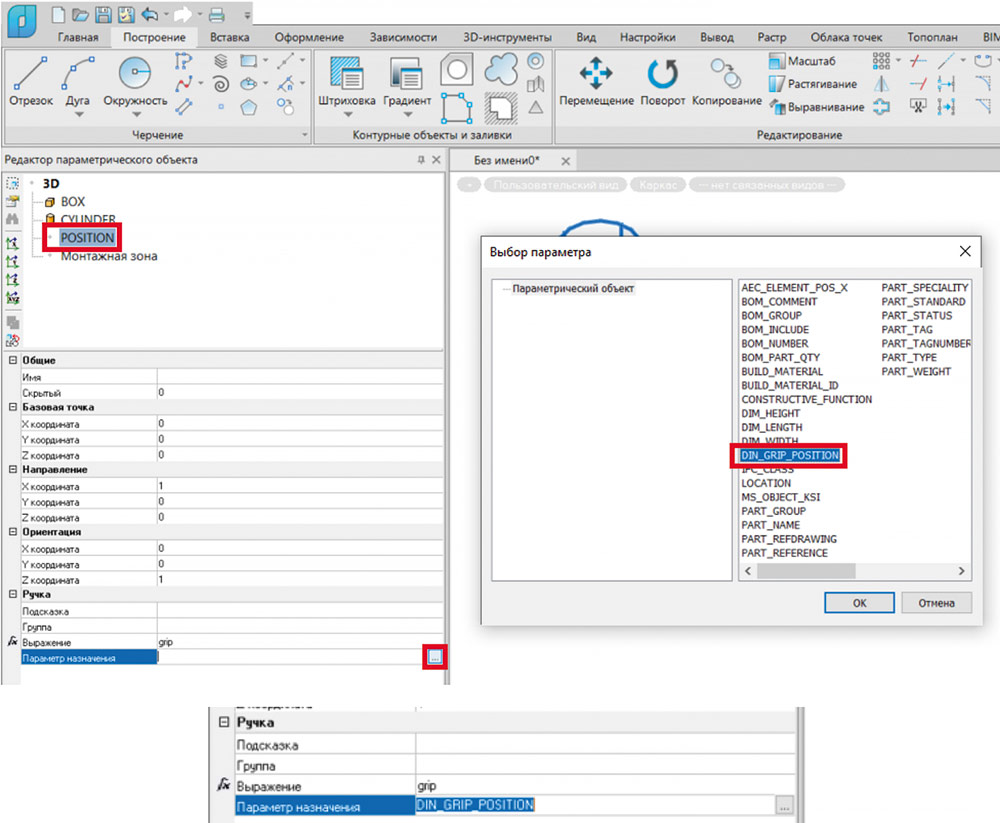
Рис. 15. Присвоение параметра назначения

Изначально «ручка» положения создается в начале локальной системы координат объекта, поэтому «ручка» перекрывается с «ручкой» точки вставки объекта. В этом случае при активации «ручки» активируется именно «ручка» положения. Активируем «ручку» и переместим ее в какое-то другое место (рис. 16).

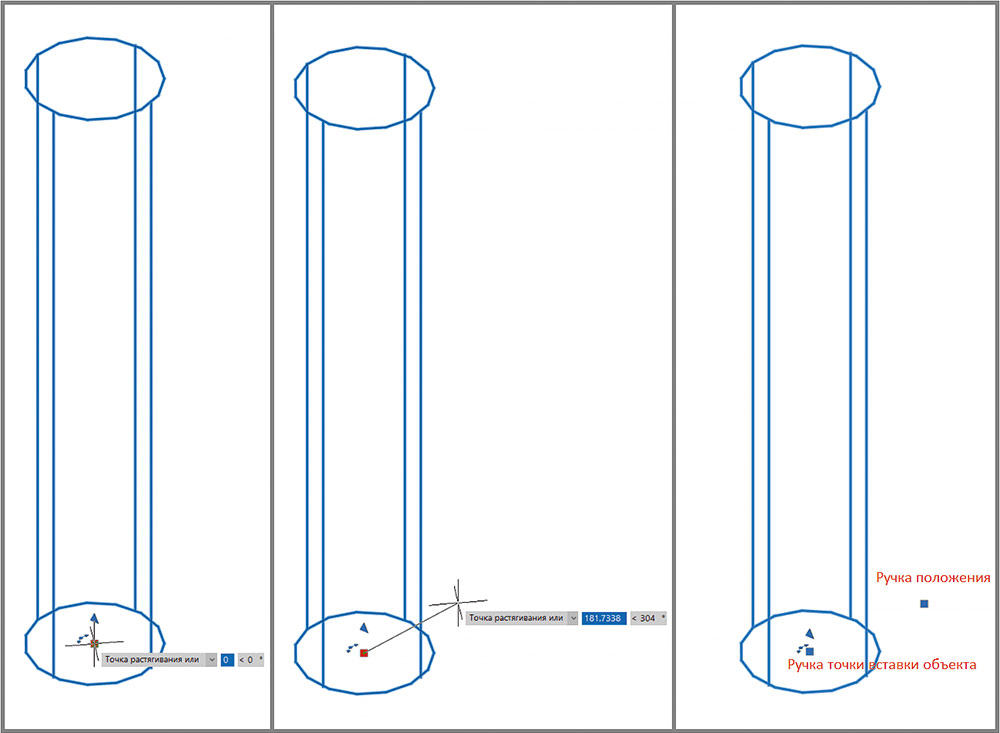
Рис. 16. Перемещение «ручки» положения

После этого в свойствах объекта начнут отображаться координаты «ручки» положения. Значения координат соответствуют положению точки относительно локальной системы координат объекта (рис. 17).

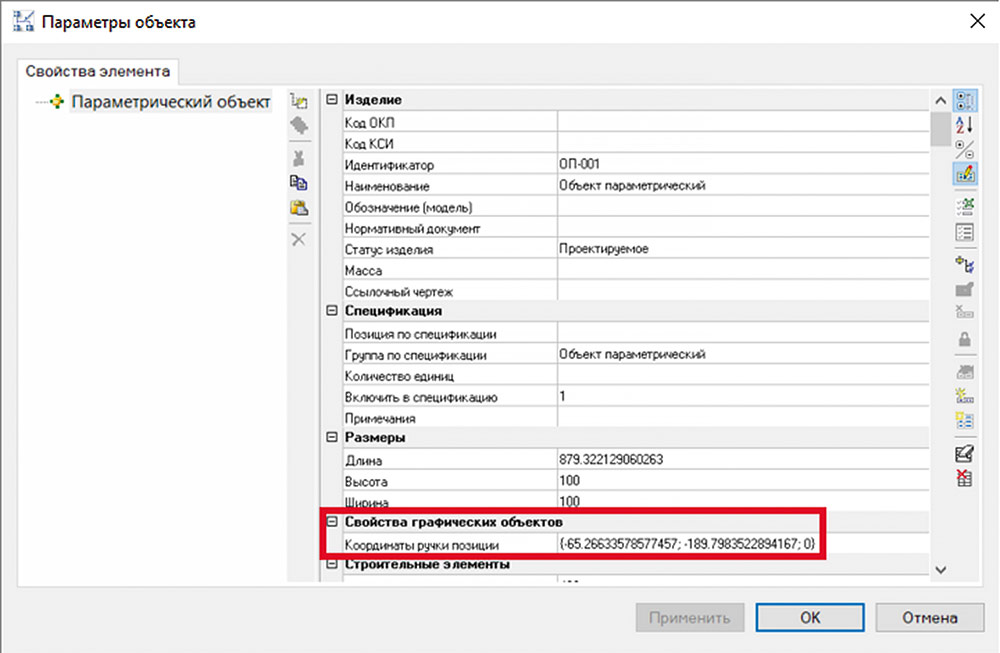
Рис. 17. Значение координат «ручки» положения

Значение параметра содержит координаты по трем осям (X, Y, Z). Этих трех значений вполне достаточно для параметризации точки положения примитива объекта. Пропишем эти значения в свойствах базовой точки примитива. Для этого снова воспользуемся Мастером функций (рис. 18).

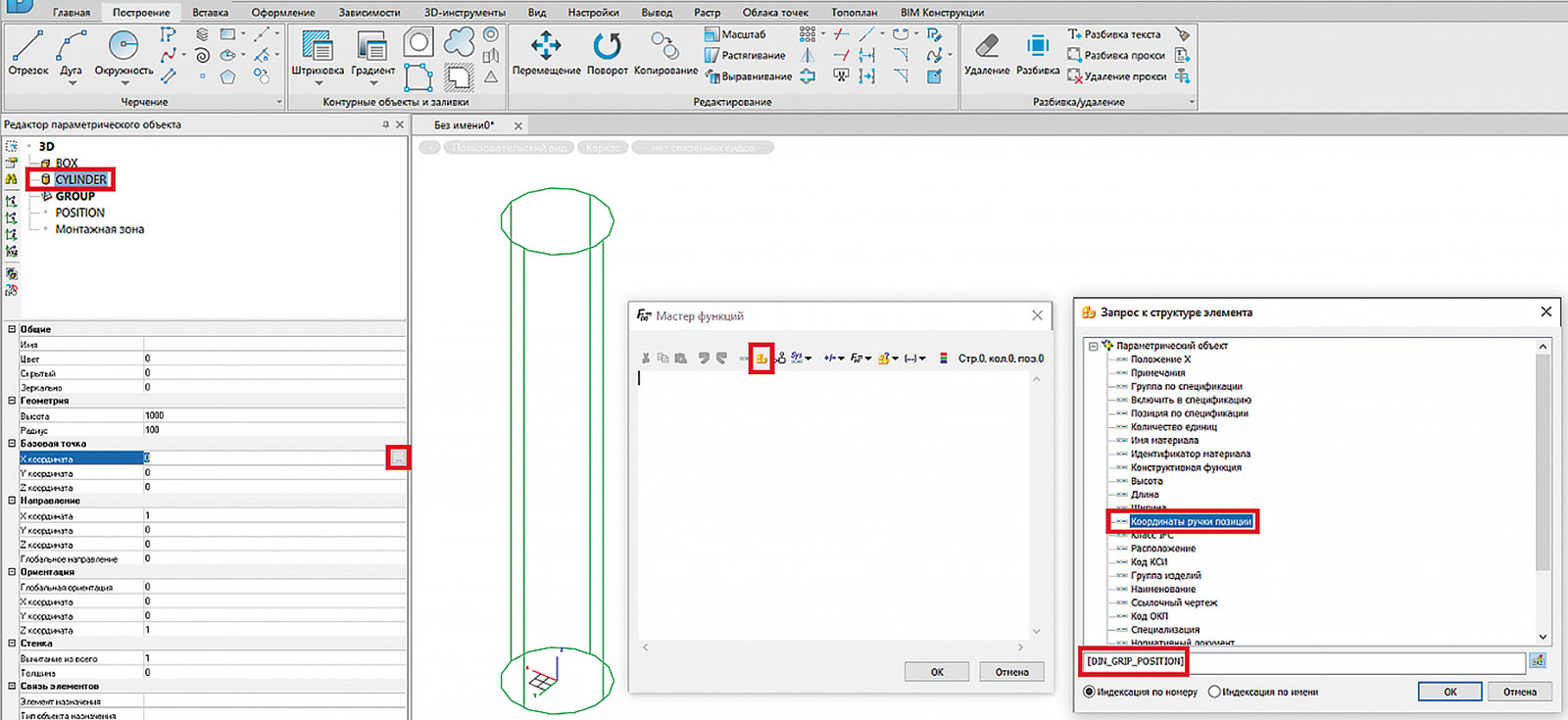
Рис. 18. Параметризация базовой точки
с использованием координат «ручек» положения

Если просто вставить параметр [DIN_GRIP_POSITION] в Мастер функций, то значение будет приходить в виде тройки значений координат {X, Y, Z}, что не подходит для решения поставленной задачи, так как в этой ситуации параметризуется значение координаты по оси X (рис. 19).

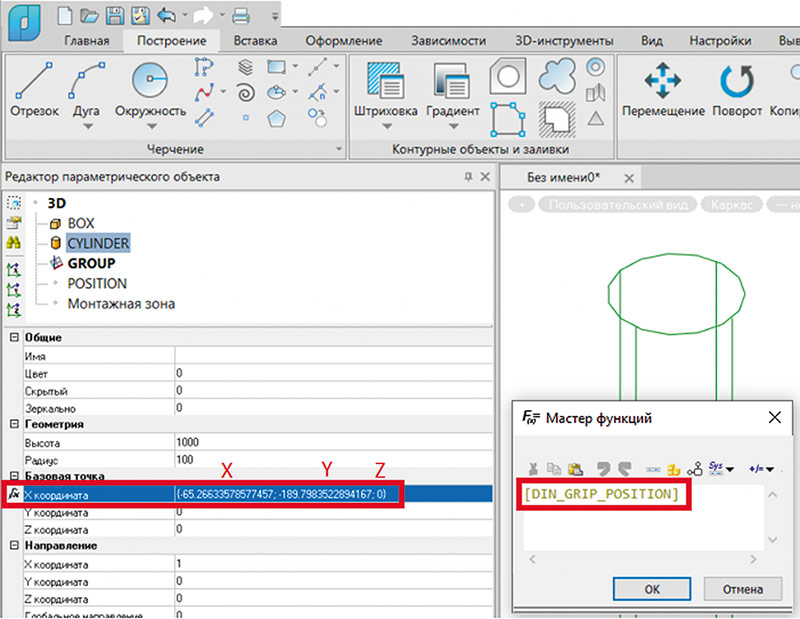
Рис. 19. Координаты «ручки» позиции

Поэтому из тройки координат {X, Y, Z} необходимо получить значение первой координаты по оси X. Для этого можно воспользоваться функцией vector(), которая позволяет получить значение координаты по ее индексу (рис. 20). Также эта функция позволяет создать векторный тип данных по значению трех числовых аргументов.

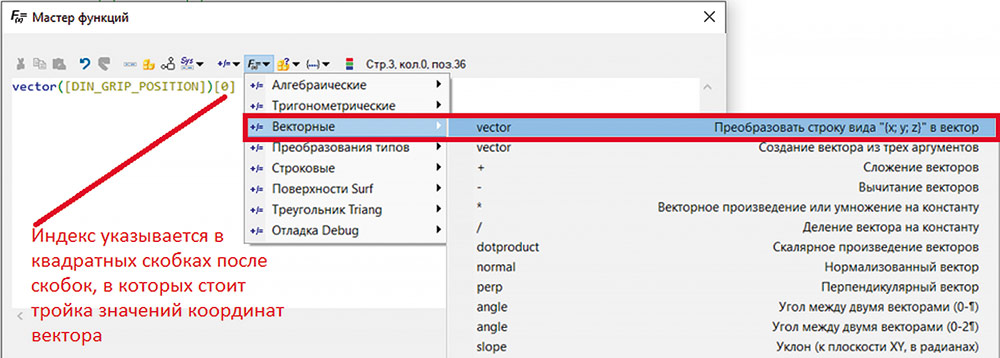
Рис. 20. Получение значения координаты по индексу с помощью функции vector()

Индекс, равный:

• 0 соответствует координате X;
• 1 соответствует координате Y;
• 2 соответствует координате Z.

Теперь в значение по X базовой точки примитива будет приходить значение по X «ручки» положения (рис. 21).

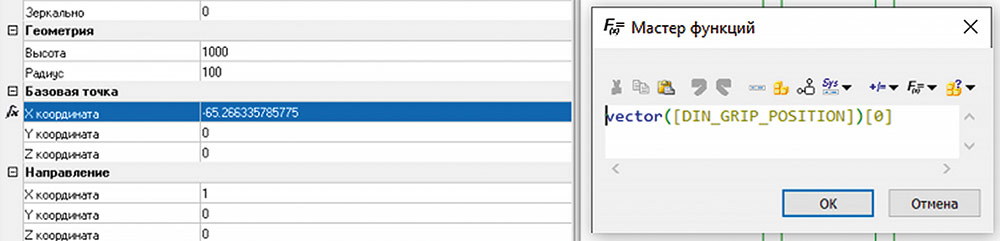
Рис. 21. Пример получения координаты по оси X

Пропишем аналогичные функции для координат базовой точки по Y и Z. Для этого потребуется поменять индексы в квадратных скобках (рис. 22).

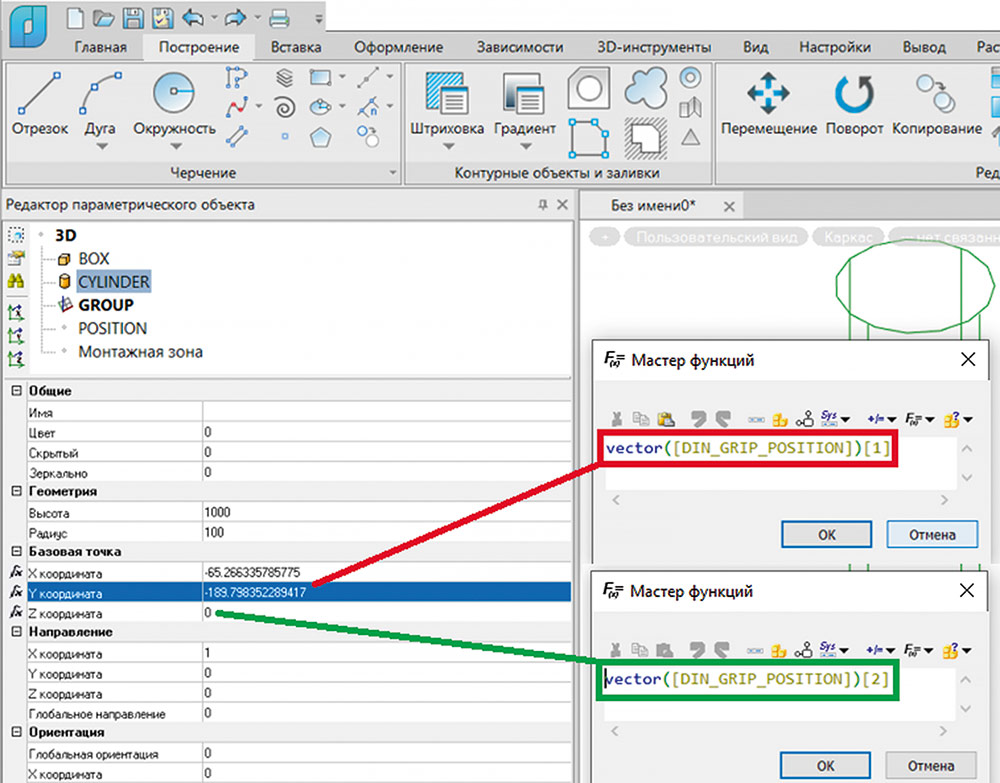
Рис. 22. Пример получения координат по осям X и Y

Теперь начало системы координат примитива объекта (в данном случае цилиндра) совпадает с координатами «ручки» положения. Активация и перемещение «ручки» положения также будут перемещать и примитив (рис. 23), аналогично тому, как работает «ручка» вставки объекта, с той лишь разницей, что «ручка» вставки объекта перемещает объект относительно мировой системы координат, а «ручка» положения перемещает часть примитива относительно локальной системы координат объекта (точки вставки объекта).

Рис. 23. Перемещение примитива объекта с помощью «ручки» положения

Научившись целиком перемещать графические примитивы объекта, разберемся, как редактировать части графических примитивов. Большая часть графических примитивов имеет заранее заданные параметры, редактирование которых с помощью «ручки» положения является избыточным, так как эти параметры зачастую можно редактировать при помощи «ручек» длины или смещения, что в плане параметризации является более лаконичным решением (рис. 24).

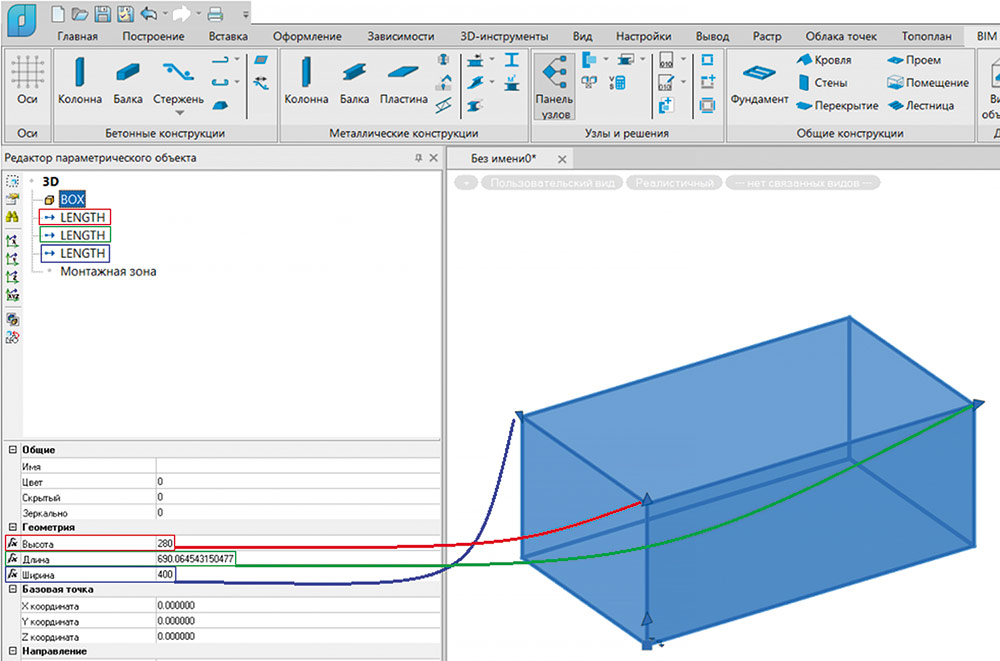
Рис. 24. Пример параметризации габаритов BOX с помощью «ручек» длины

Также большая часть примитивов имеет ограничения в плане геометрии. Например, для примитива BOX нет возможности редактировать положения вершин объекта таким образом, чтобы из прямой призмы получались другие варианты четырехугольных призм. Однако в Редакторе параметрического объекта есть возможность использовать не только примитивы с заранее заданными контурами оснований, но и инструменты 3D-выдавливания по контуру, аналогично тому, как это делается инструментами 3D-моделирования 3D-модуля Платформы nanoCAD (команды: 3dextrude, 3drevolve, 3dsweep).

Параметризация положения точки контура элемента 3D-выдавливания

Рассмотрим процесс создания элемента выдавливания и параметризацию его контура. Чтобы создать элемент выдавливания, необходимо выбрать соответствующий элемент в контекстном меню (рис. 25).

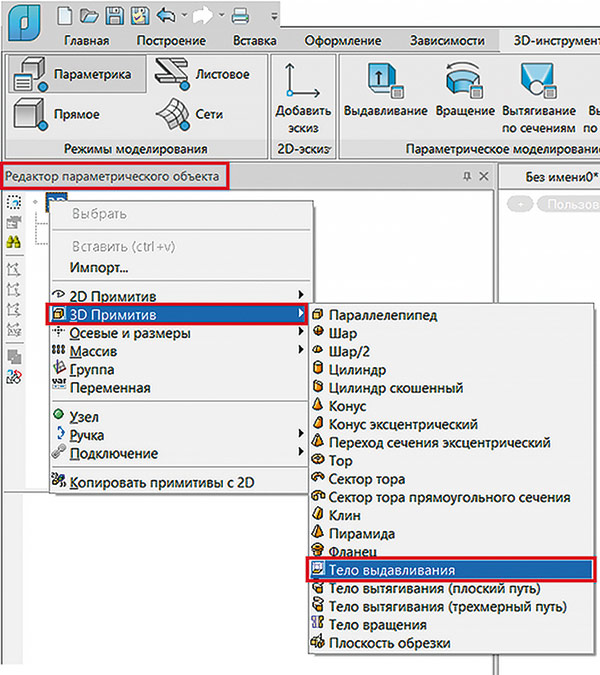
Рис. 25. Добавление тела выдавливания

В дереве построения Редактора параметрического объекта появится соответствующий элемент. Тело выдавливания Extrusion имеет параметры, которые позволяют задавать положение примитива относительно локальной системы координат и высоту выдавливания контура. Если развернуть Extrusion, нажав на значок +, можно увидеть контур, по которому формируется элемент выдавливания. По умолчанию создается цилиндр с контуром выдавливания по дуге. Контур выдавливания (в данном случае дуга) также имеет геометрические параметры, меняя которые можно менять все тело выдавливания (рис. 26).

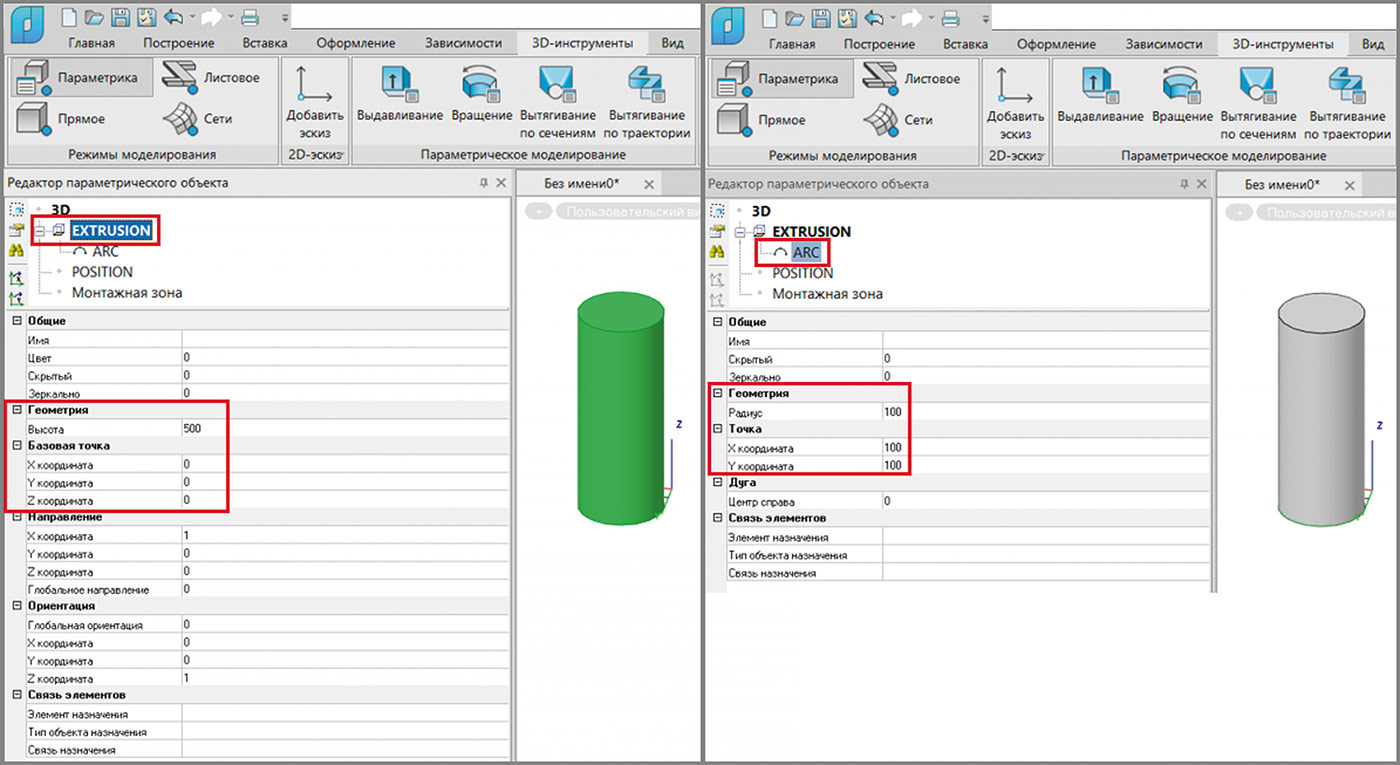
Рис. 26. Геометрические параметры тела выдавливания

Давайте поменяем контур с окружности на прямоугольник. Для этого необходимо удалить имеющийся контур (рис. 27) и импортировать новый.

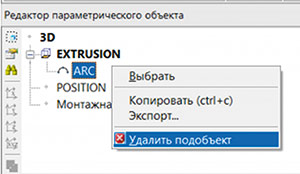
Рис. 27. Удаление контура в теле выдавливания

Чтобы импортировать контур, его необходимо предварительно отрисовать в пространстве модели, например, отрезками или полилинией. После этого данный контур нужно выделить, а для операции выдавливания вызвать контекстное меню правой кнопкой мыши. В контекстном меню необходимо выбрать пункт Выбрать 2DПрофиль (рис. 28).

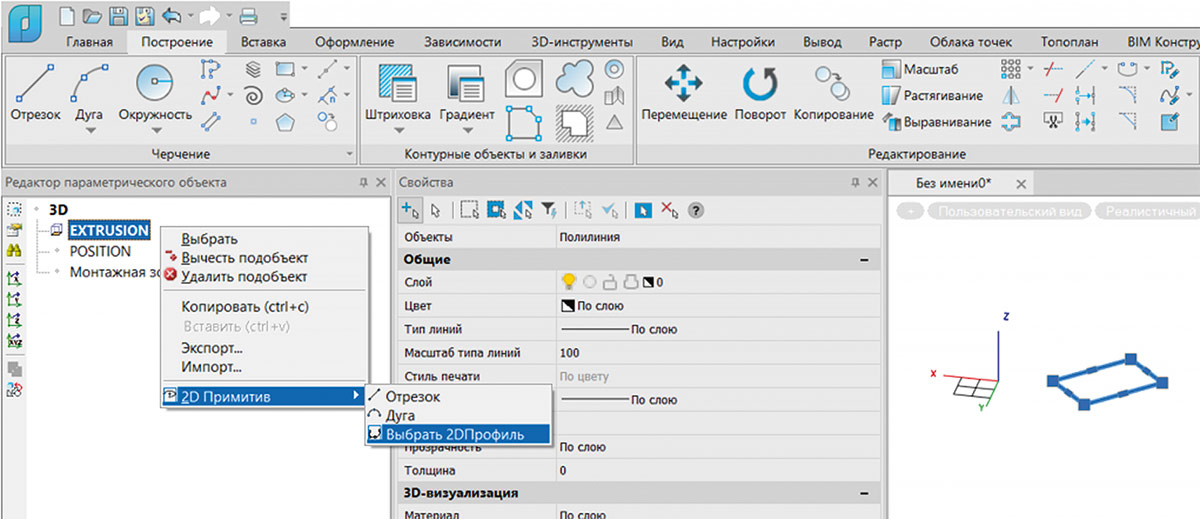
Рис. 28. Активация команды импорта профиля

После этого в командной строке появится запрос на указание базовой точки. Укажем в качестве базовой точки одну из вершин полилинии (рис. 29).

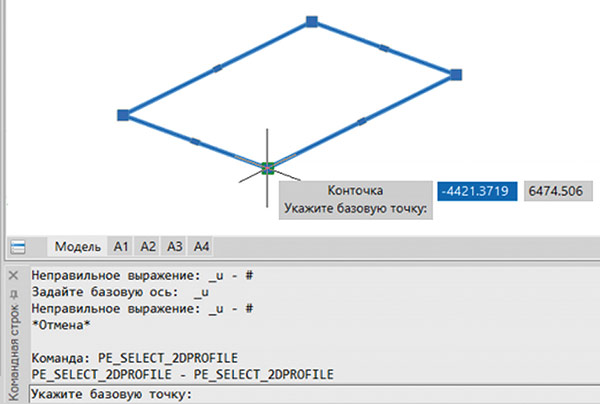
Рис. 29. Выбор базовой точки импортируемого профиля

Затем необходимо указать направление оси X создаваемой системы координат примитива. Логично направить ее вдоль какой-либо стороны контура (рис. 30).

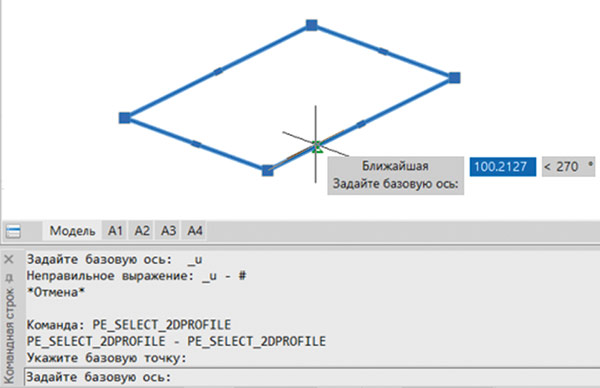
Рис. 30. Выбор направления базовой оси импортируемого профиля

В результате в теле выдавливания появится новый контур, по которому сформируется новое тело выдавливания — прямая призма. Примечательно, что тело выдавливания в этом случае состоит из четырех отрезков, а не цельной полилинии, и у каждого отрезка есть точка положения, причем только одна. Учитывая эту особенность, правильнее будет воспринимать отрезки как вершины контура (рис. 31).

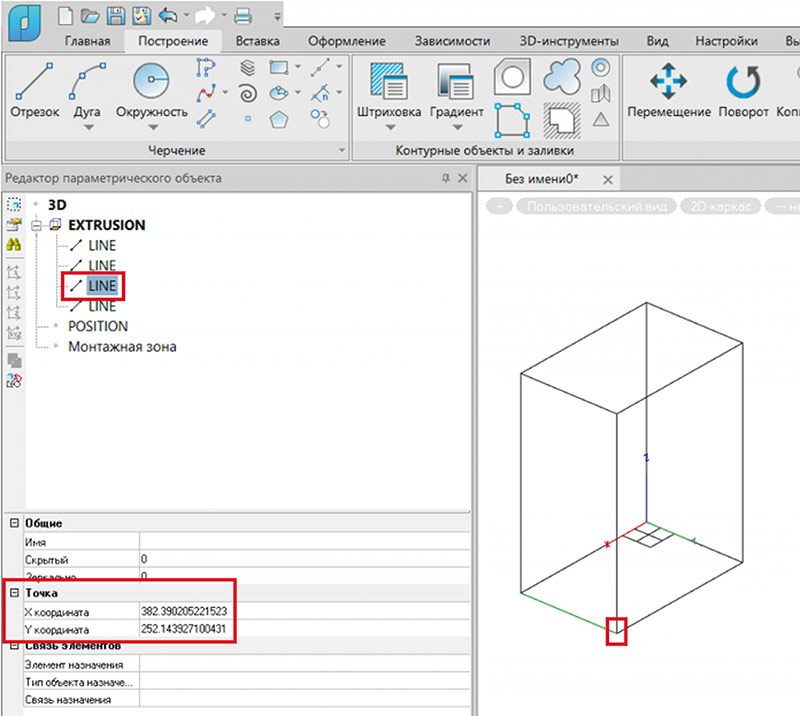
Рис. 31. Параметры точек импортированного профиля выдавливания

Очевидно, что точка имеет две координаты по X и Y, которые также можно параметризовать «ручкой» положения. Если параметризация подразумевает, что меняется только одна координата вдоль какой-либо оси, то для параметризации проще будет использовать «ручку» длины или смещения. Но в нашей статье параметризация этих «ручек» не рассматривается, так как по работе с ними уже есть довольно много справочных материалов, ссылка на один из них дана в начале статьи. А в случае, если необходимо менять положение точки контура по двум координатам, удобно использовать «ручку» положения.

Создадим «ручку» положения и в качестве параметра назначения снова укажем [DIN_GRIP_POSITION], а также передадим координаты «ручки» в соответствующие координаты точки контура (рис. 32).

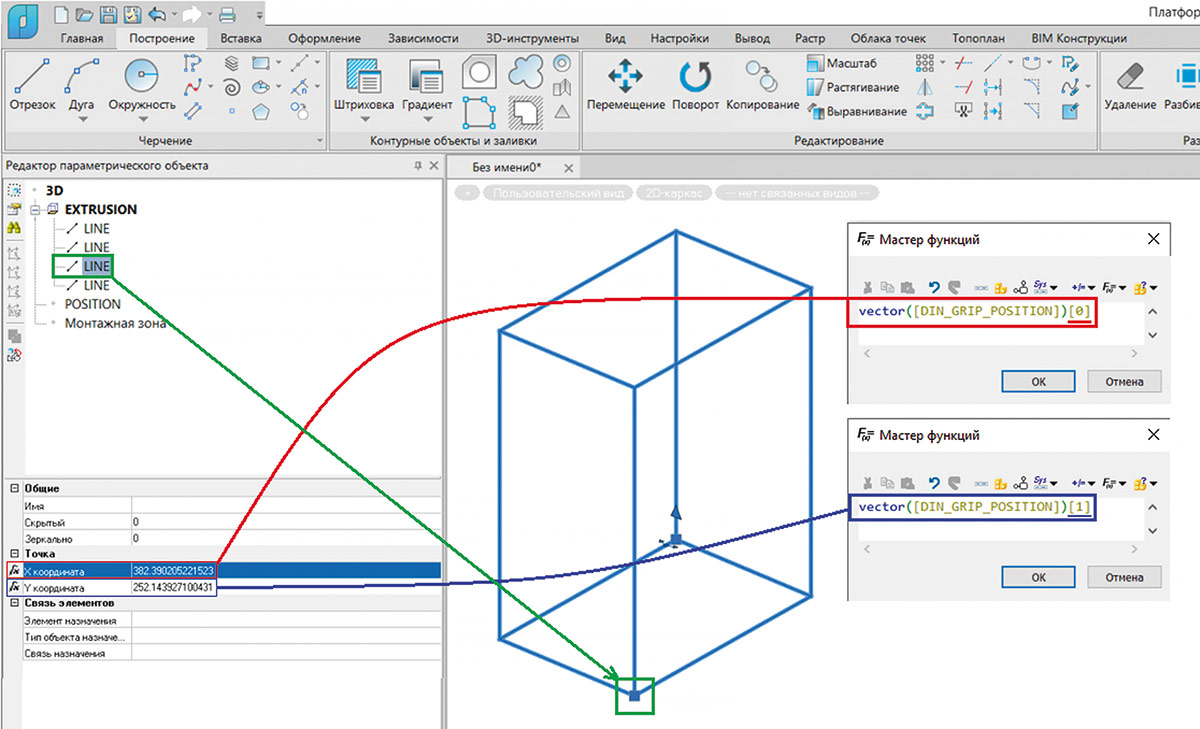
Рис. 32. Параметризация точки контура с помощью «ручки» положения

Попробуем переместить «ручку» положения, чтобы увидеть, как изменится тело при изменении положения точки контура (рис. 33).

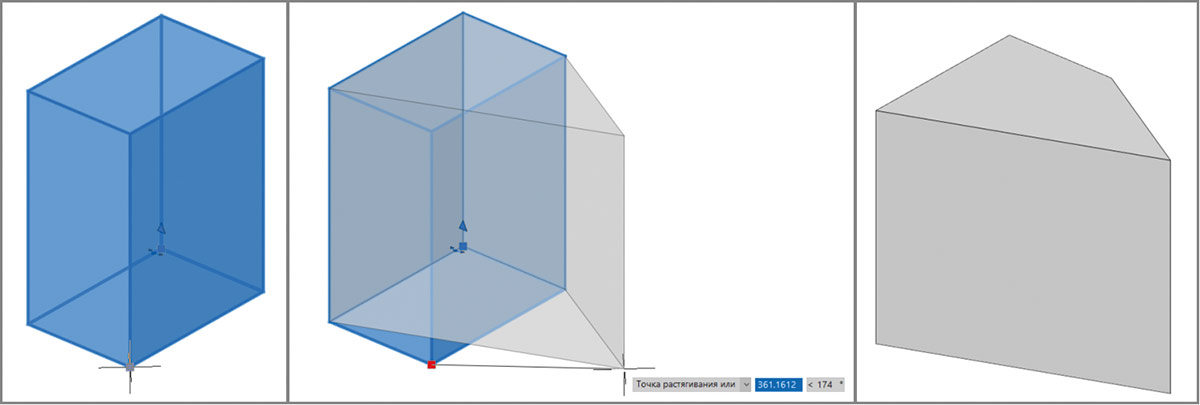
Рис. 33. Изменение контура с помощью «ручки» положения

Важно отметить, что точки контура подразумевают параметризацию только по осям X и Y, а как можно было видеть ранее, «ручка» положения передает координаты в том числе по оси Z. Поэтому если перемещать «ручку» положения, задавая и значение координаты по оси Z, то «ручка» положения оторвется по оси Z от вершины, которую она параметризует (рис. 34).

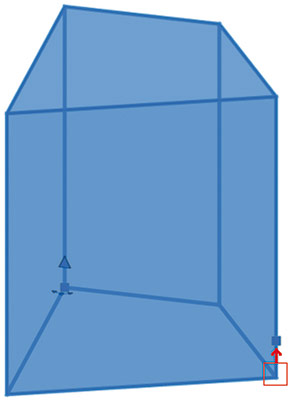
Рис. 34. Смещение «ручки» по оси Z

Чтобы избежать этого, необходимо ограничить возможность перемещения «ручки» положения по оси Z. Сделать это можно с помощью параметра Выражение. Этот параметр позволяет пересчитать значение, которое «ручка» передает в параметр [DIN_GRIP_POSITION] объекта (рис. 35).

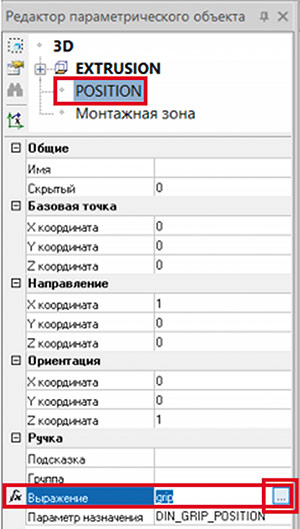
Рис. 35. Параметр Выражение для «ручки» положения

Параметр Выражение также можно параметризовать в окне Мастера функций, если нажать на соответствующее троеточие. По умолчанию в параметре Выражение имеется переменная grip, которая хранит значение, передаваемое «ручкой» (рис. 36).

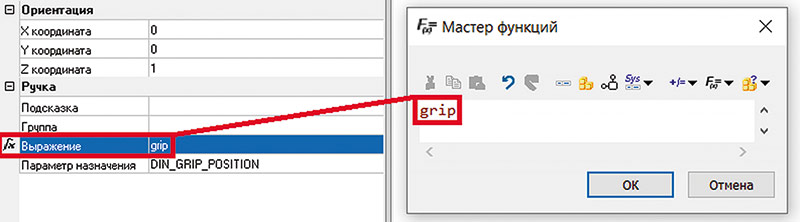
Рис. 36. Переменная grip в параметре Выражение

Ограничивая значения, которые передает переменная grip, можно добиться соответствующих ограничений в перемещении «ручек». Очевидно, что для «ручки» положения переменная grip хранит тройку значений координат положения «ручки» {X, Y, Z}. Координаты по X и Y в этом случае нужны для параметризации точки положения контура элемента выдавливания, а вот координата по Z должна быть равной 0, чтобы «ручка» не отрывалась по оси Z.

Функция vector() имеет два варианта применения:

• один из них уже был рассмотрен. Применение функции vector (X, Y, Z)[i] позволяет получить одно из значений координаты, хранимых внутри тройки координат {X, Y, Z}, где i — индекс считываемой координаты;
• второй вариант применения функции vector (X, Y, Z) позволяет создать тройку значений координат вектора {X, Y, Z}.

Для ограничения перемещения «ручки» положения по координате Z надо использовать оба варианта.

Необходимо передать в [DIN_GRIP_POSITION] положение «ручки» по координатам X и Y, приняв, что Z=0. Непосредственно переписать значения координат в самой переменной grip нет возможности, но значения с grip можно считать и пересчитать при помощи функции vector(X, Y, Z)[i]. И уже новые значения можно собрать с помощью функции vector (X, Y, Z).

Обеспечим передачу в параметр [DIN_GRIP_POSITION] координаты по Z=0. Для этого воспользуемся функцией vector (X, Y, Z). Использование этой функции показано на рис. 37.

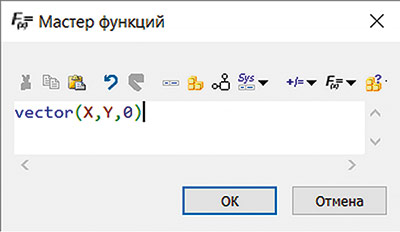
Рис. 37. Использование функции vector (X, Y, Z) для создания вектора по трем координатам

Пока что функция не передает никаких значений по осям X и Y. Эти значения возьмем из переменной grip c помощью уже знакомой нам функции vector (X, Y, Z)[i]:

• X — vector(grip)[0];
• Y — vector(grip)[1].

Таким образом, в параметр [DIN_GRIP_POSITION] передаются координаты по осям X и Y от «ручки» положения, а координата по Z=0. Формула показана на рис. 38.

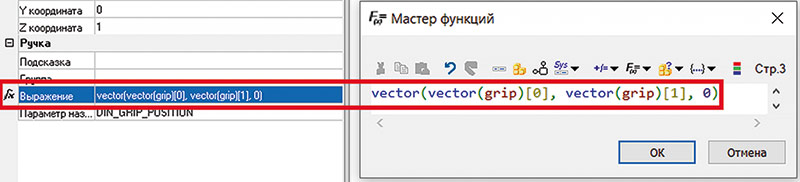
Рис. 38. Итоговая формула для параметра Выражение

Примечательно, что такая параметризация не просто передает в [DIN_GRIP_POSITION] пересчитанное значение координат «ручки» положения, но и влияет на поведение самой «ручки». В этом случае «ручка» больше не имеет возможности перемещаться по координате Z, независимо от того, как она будет перемещаться в пространстве модели: c режимом ОРТО, полярным отслеживанием по Z, вводом относительных или абсолютных координат. Координата «ручки» по Z всегда будет равна 0 относительно локальной системы координат объекта (рис. 39). 

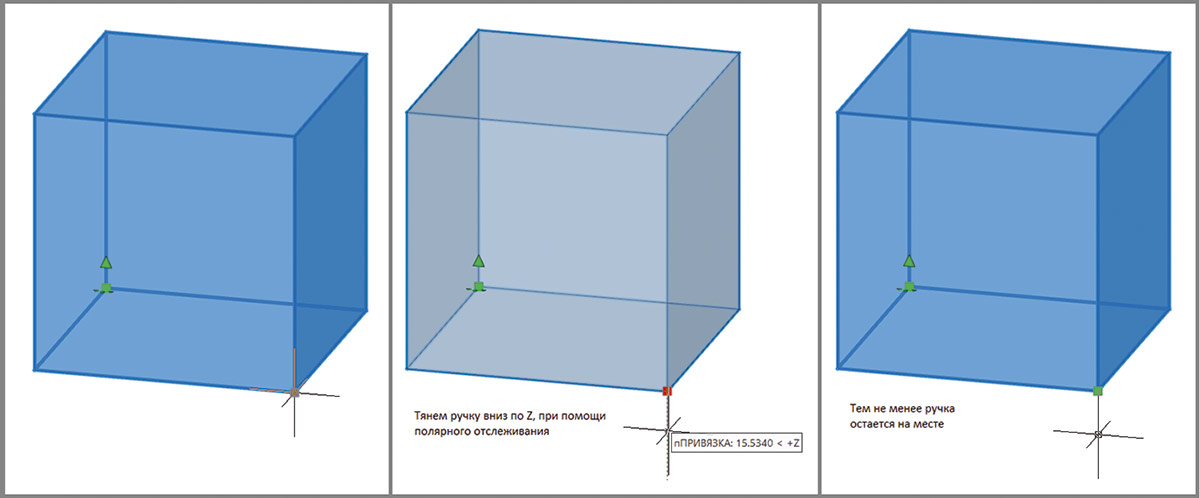
Рис. 39. Параметризованное Выражение

 Узнайте подробнее о nanoCAD BIM Строительство: