Траектории Мёбиуса в КОМПАС-3D

Александр Стремнев,
к.т.н., доцент кафедры информационных технологий Белгородского государственного технологического университета им. В.Г. Шухова

Лучший способ проверить функциональность программного обеспечения для работы с геометрией — это попробовать реализовать в нем такую форму, само существование которой сложно себе представить. Загадочные поверхности Августа Фердинанда Мёбиуса и КОМПАС-3D. Кто кого? Или в этом противостоянии возможен паритет?

Лента (кольцо, петля) Мёбиуса — широко известный пример так называемой односторонней поверхности. Она характеризуется тем, что, находясь на ней, можно достичь любой ее точки, не пересекая острое краевое ребро [1]. Изготовить этот нетривиальный топологический казус можно буквально за несколько секунд, перекрутив бумажную ленточку винтом вдоль продольной оси и склеив ее концы (рис. 1). Для того чтобы раскрасить такой объект с «обеих» сторон, не потребуется даже отрывать карандаша или фломастера от его поверхности.

Рис. 1

Довольно интересные объекты получаются на основе ленты Мёбиуса, если этой поверхности придать толщину и разделить образовавшийся объем в продольном направлении на несколько частей. Такие треугольники, или кольца Мёбиуса, на первый взгляд кажутся состоящими из отдельных частей, а на самом деле представляют собой замысловатые спирально-винтовые объекты (рис. 2).

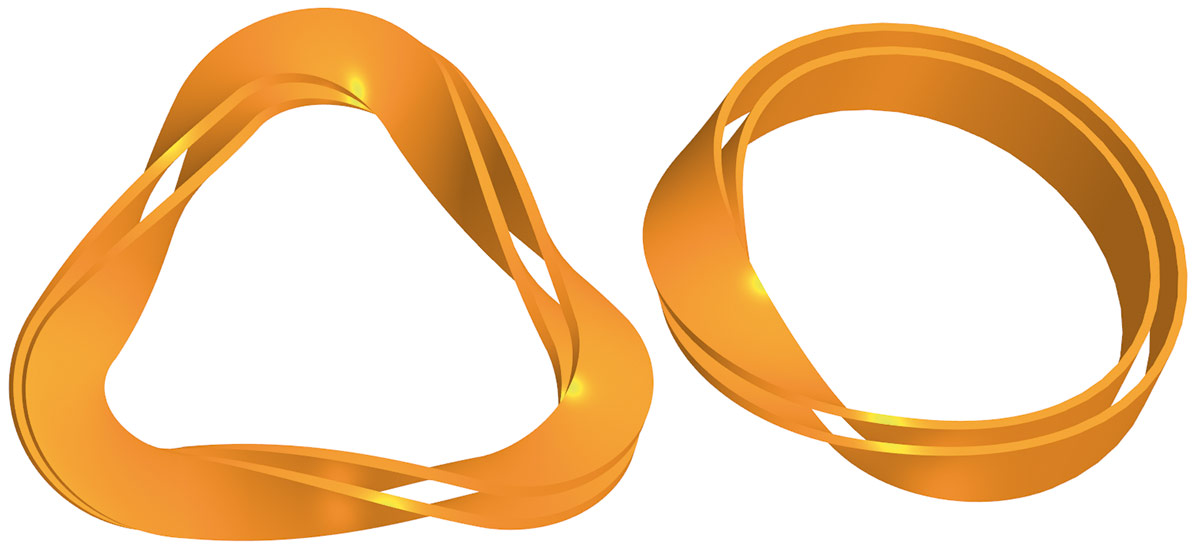
Рис. 2

Попробуем разобраться, как такие фигуры реализуются в САПР, например КОМПАС-3D [2]. Начнем с объекта Мёбиуса, напоминающего треугольник. В качестве основного инструмента будем использовать Элемент по траектории (рис. 3). В базовом варианте эта команда требует указания только поперечного сечения и траектории, вдоль которой будет «перемещаться» сечение, образуя необходимую объемную геометрию. В связи с особенностью формы модели в качестве траектории достаточно задать одну третью часть контура треугольника (см. рис. 2, вид слева). Полученная таким образом с помощью Элемента по траектории форма не имеет продольной крутки и поэтому в таком виде для воплощения геометрии Мёбиуса не годится (см. рис. 3, врезка справа).

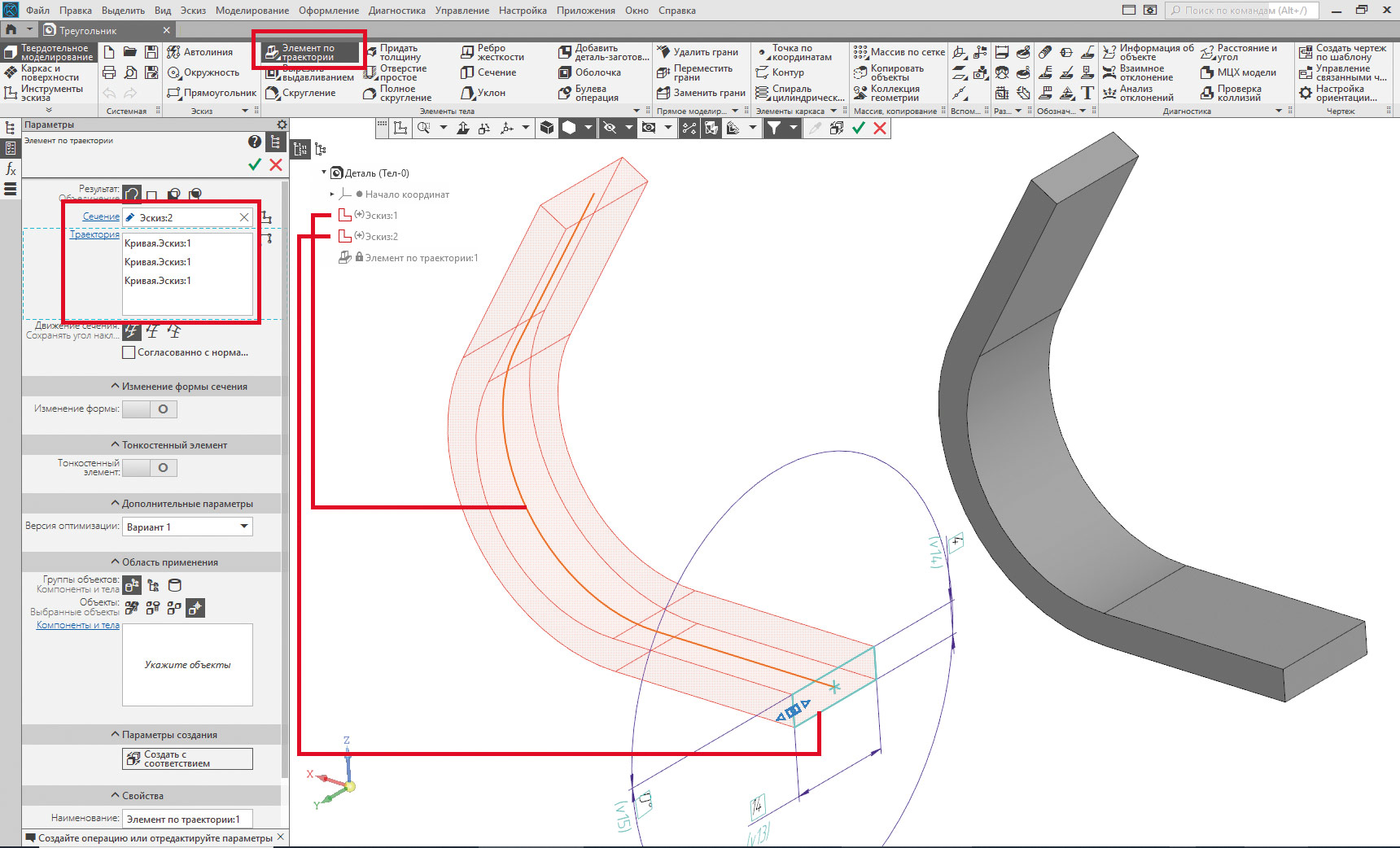
Рис. 3

Реализовать скручивание ленты можно, организовав вращение поперечного сечения. Для этого сначала в эскизе сечения необходимо предусмотреть параметрический размер, устанавливающий угол поворота рабочего сечения (в нашем случае прямоугольника) относительно условно горизонтального направления (рис. 4). Естественно, что при этом прямоугольник-сечение ни по одной стороне не должен иметь ограничения горизонтальности или вертикальности.

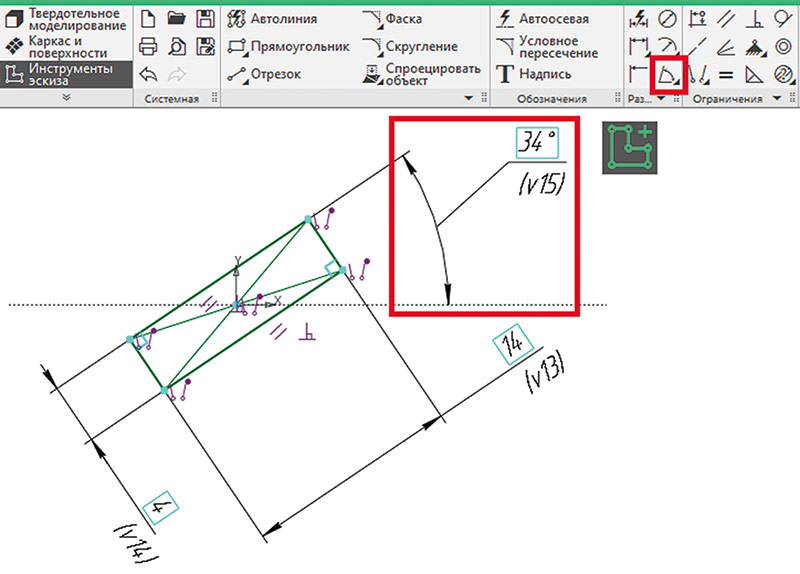
Рис. 4

Теперь в команде Элемент по траектории нужно включить режим Изменение формы сечения (рис. 5). Изменение будет заключаться в повороте сечения при его «движении» вдоль траектории. Нажатием кнопки Читать переменные в окне команды мы получаем доступ к переменным-параметрам, определяющим геометрию сечения. В таблице выбираем угловой размер-параметр, а в разделе Тип функции задаем вариант Линейная. И наконец, в полях Начальное значение и Конечное значение вводим величину угла поворота сечения соответственно в начальной и конечной точках траектории. «Перекрутить» фрагмент «ленты» треугольника достаточно на половину оборота, то есть на угол от 0 до 180 градусов (см. рис. 5).

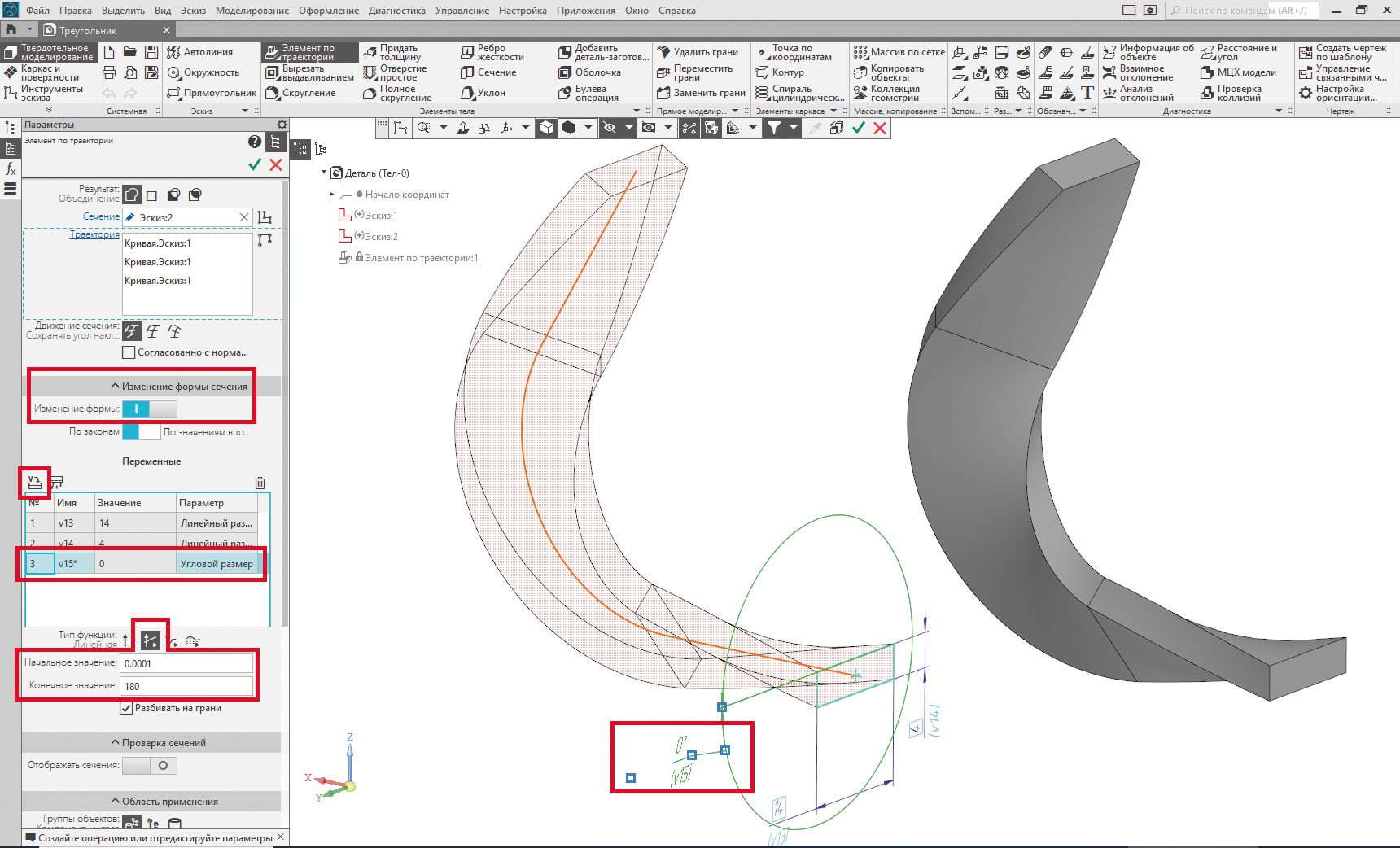
Рис. 5

Завершенный треугольник Мёбиуса получаем троекратным дублированием полученного элемента посредством команды Массив по концентрической сетке относительно рабочей оси, проведенной через точку геометрического центра (рис. 6). Следует обратить внимание на гладкость стыков между копиями исходного элемента (см. рис. 6, врезка справа). Это достигается за счет того, что каждый следующий элемент «по сечениям» как бы продолжает скручивание предыдущего.

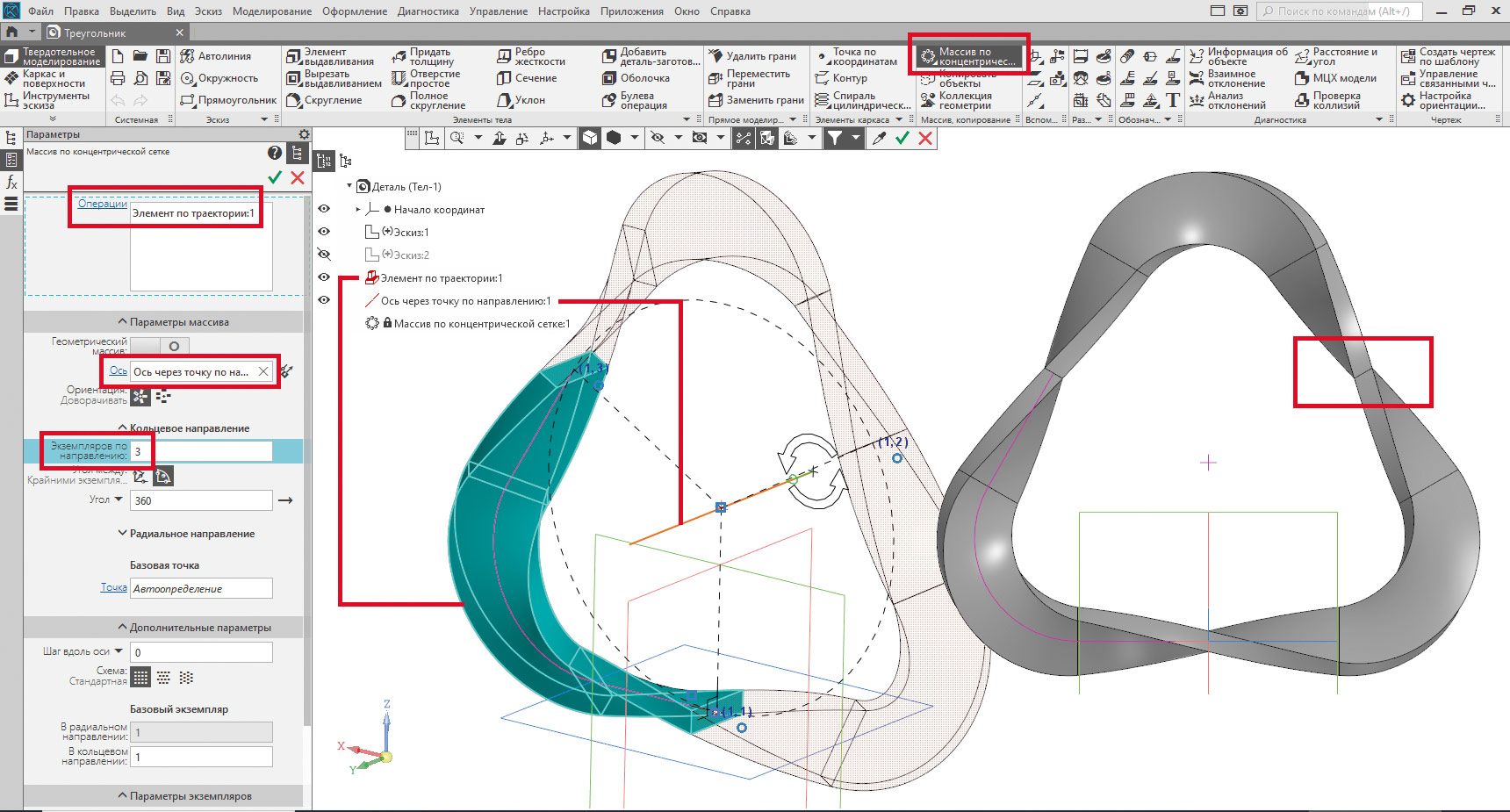
Рис. 6

Теперь реализуем объект Мёбиуса в форме кольца (см. рис. 2, вид справа). Общий план построения будет заключаться в создании двух половин кольца, одна из которых представляет собой обычный «элемент по траектории» без крутки. Второму же «элементу по траектории» зададим скручивание аналогично методике, опробованной для треугольника, — линейным изменением угла поворота сечения от 0 до 180 градусов. В отличие от треугольника соединяемые половинки кольца имеют различный характер крутки (в одной крутка отсутствует, а в другой она равномерно увеличивается от 0 до 180 градусов), поэтому в месте стыка наблюдается их негладкое сопряжение в связи с различным характером изменения кривизны смежных участков (см. рис. 7, врезки справа).

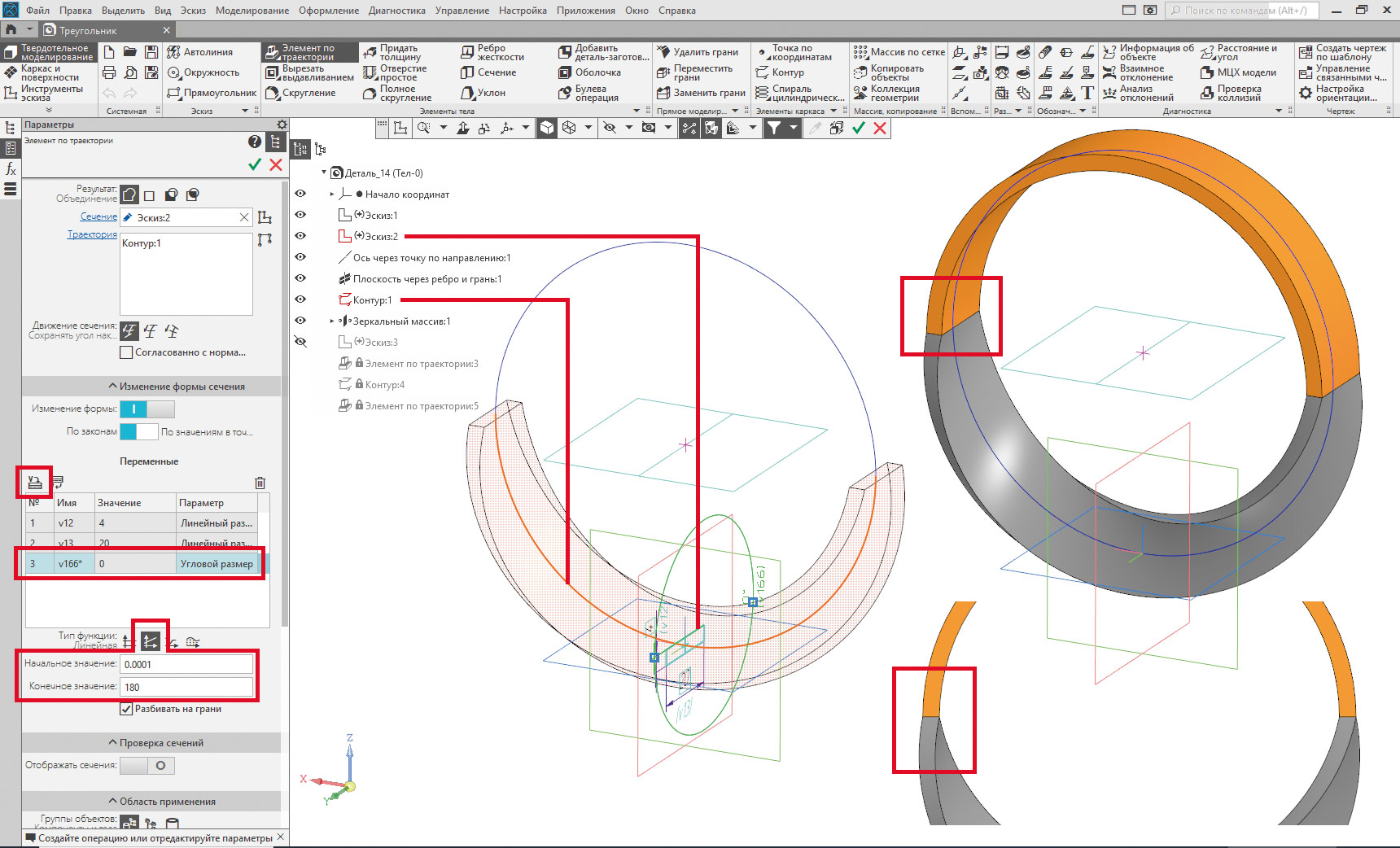
Рис. 7

Ключевым моментом, влияющим на «негладкость» стыка двух половинок кольца, является именно РАВНОМЕРНОСТЬ изменения угла поворота сечения на траектории. Если бы удалось это изменение «начинать» и «заканчивать» плавно, то стык между скрученным и гладким сегментом стал бы незаметен. Одним из способов управления параметром является построение графика, вдоль вертикальной оси которого откладываются целевые значения, соответствующие относительным позициям сечения на траектории (горизонтальная ось). В нашей задаче эскиз, содержащий этот график, имеет в целом форму наклонной линии в одной из крайних точек, проходящей через вертикальную отметку 180, а в другой — лежащей на горизонтальной оси, то есть соответствующей 0 (рис. 8). Эти отметки будут определять общий характер вариации параметра угла поворота (от 0 до 180 градусов), а плавность данного изменения зададут сопряжения наклонной линии с направлением горизонтали в крайних точках. Величина радиуса этих сопряжений будет влиять на степень плавности начала и завершения изменения параметра кручения (см. рис. 8, размер R130).

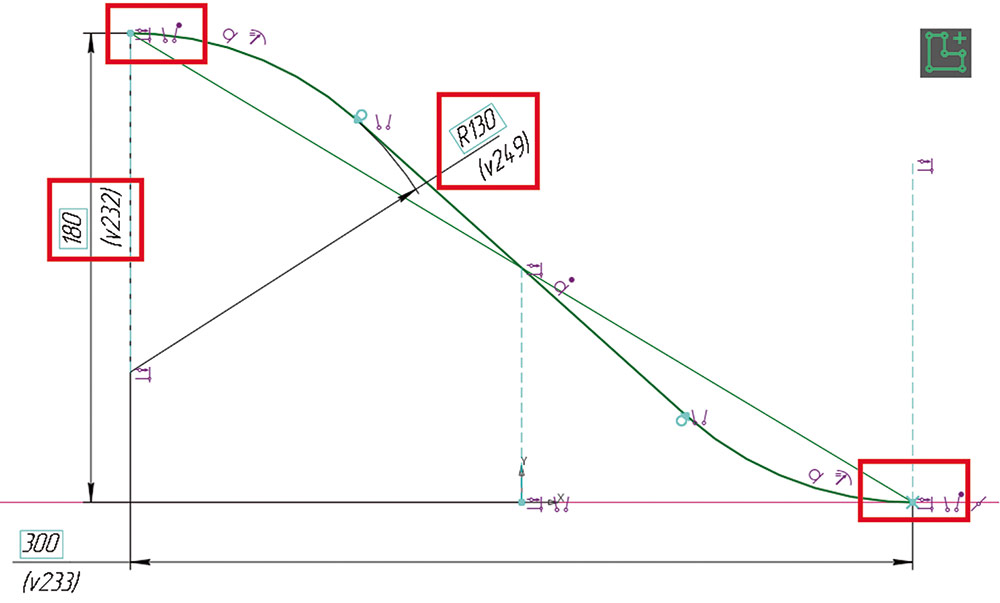
Рис. 8

Когда эскиз-график готов, откорректируем настройки скрученного «элемента по траектории» кольца Мёбиуса. Только теперь для выбранного размерного параметра, определяющего угол поворота сечения, в разделе Тип функции задаем вариант По закону кривой, а в качестве этой кривой укажем эскиз-график (рис. 9). В результате скручивание сегмента кольца будет начинаться и заканчиваться плавно, и за счет этого стык со смежным нескрученным сегментом окажется гладким (см. рис. 9, врезка справа).

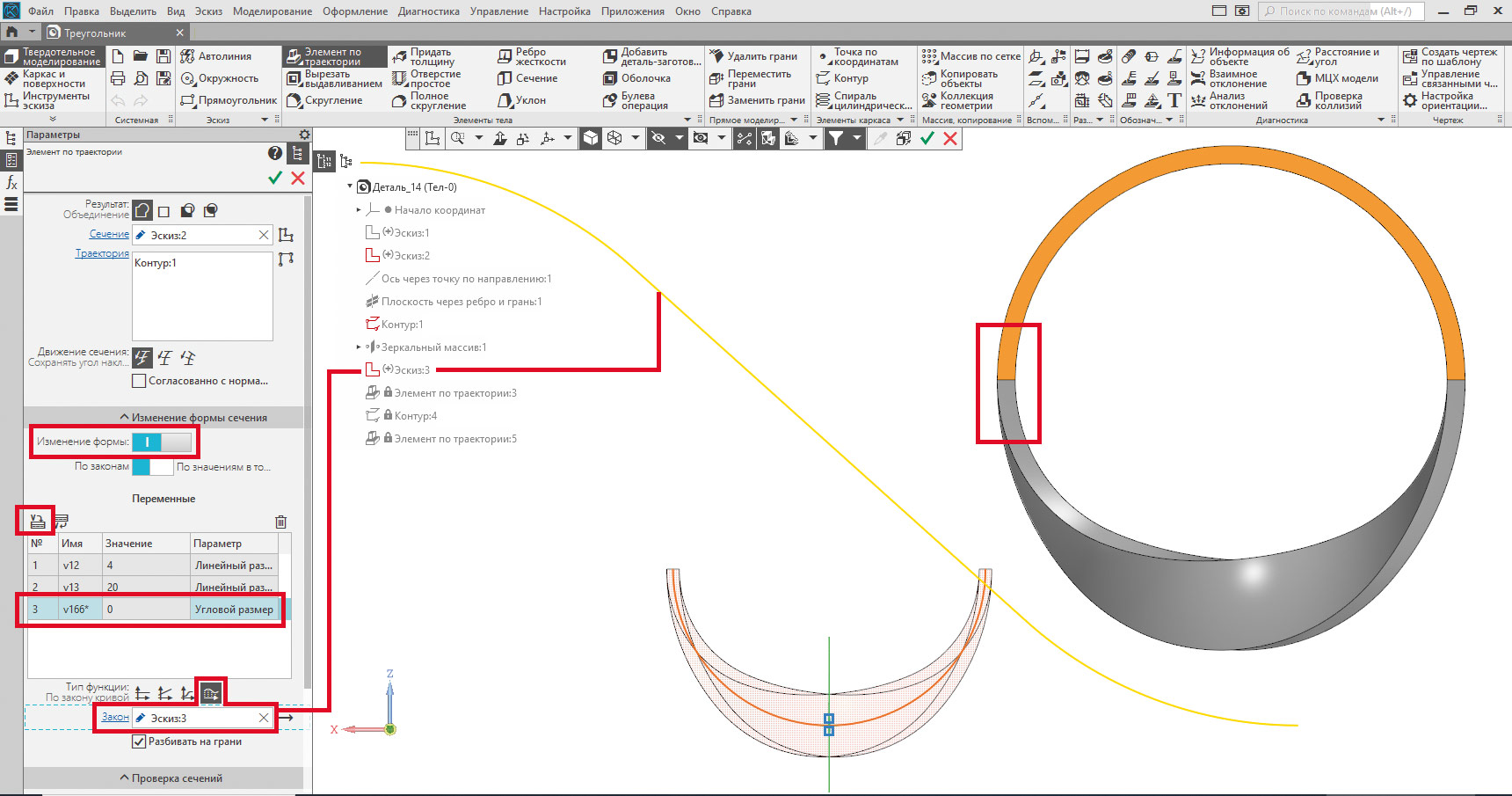
Рис. 9

В дополнение к визуальному контролю места сопряжения можно использовать специальную команду КОМПАС-3D: Диагностика -> Проверка гладкости. Налагаемая при этом на модель служебная текстура-зебра наглядно продемонстрирует отсутствие искажений формы на участке сопряжения элементов кольца Мёбиуса (рис. 10).

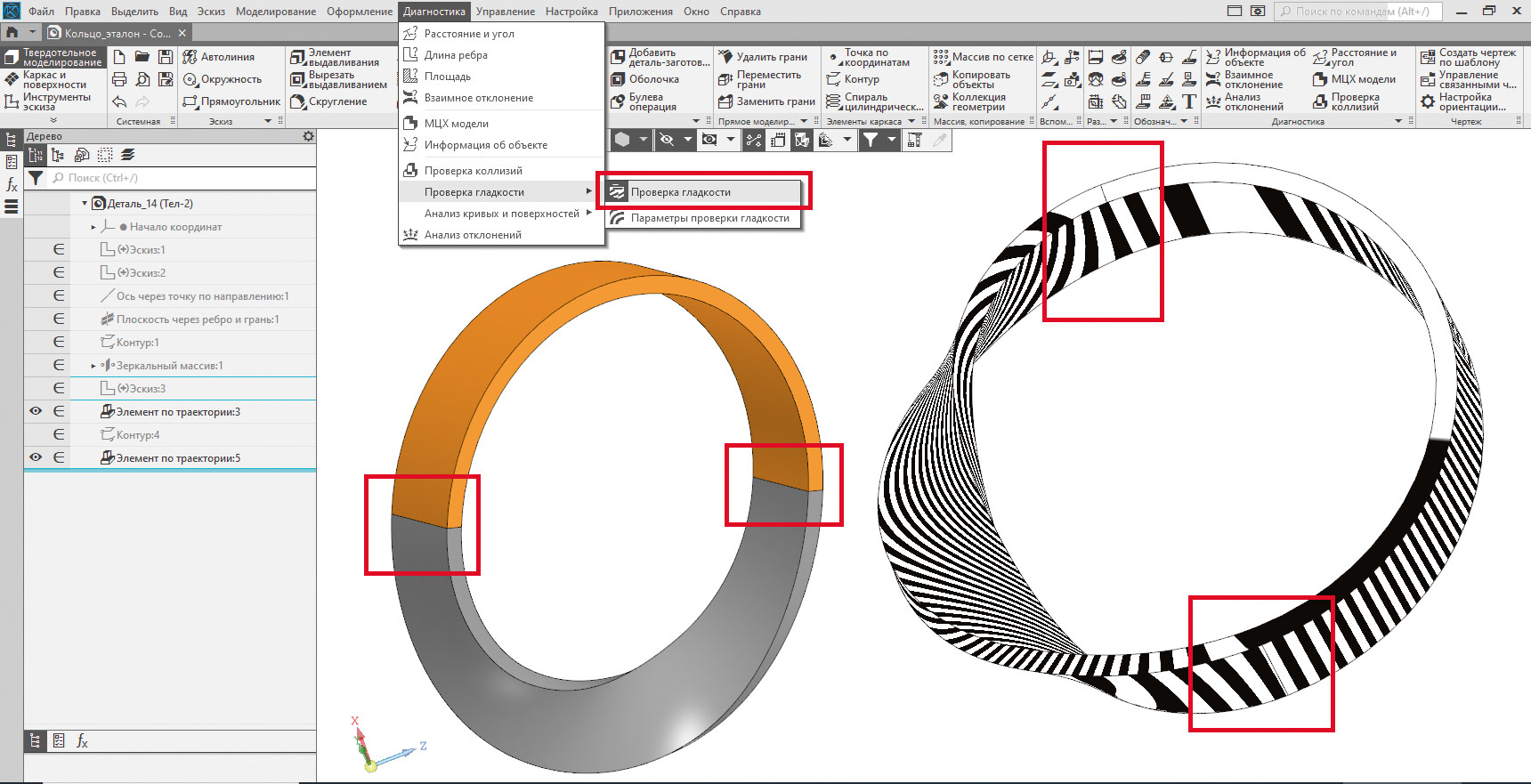
Рис. 10

Таким образом, не слишком сложная на первый взгляд задача моделирования одностороннего топологического объекта дала повод обратить пристальное внимание на детальные настройки команды Элемент по траектории системы КОМПАС-3D. А что касается двоящихся фигур Мёбиуса (см. рис. 2), то подсказкой для их реализации будет команда Придать толщину граням рассмотренных выше моделей [3].

Полезные ссылки:

1. Математическая продлёнка. Вокруг ленты Мёбиуса / Сергей Самойленко // https://habr.com/ru/articles/832098/
2. КОМПАС-3D — Система трехмерного моделирования // https://ascon.ru/products/kompas-3d/
3. Проект, рассмотренный в материале // https://rutube.ru/video/6911c7b4e1cc0d8eb8732bbd36c38957/