В 1-й и 2-й частях («САПР и графика» № 3 и 4’2025) мы познакомились с основами параметризации положения примитивов и начали исследовать возможности использования «ручек» в nanoCAD BIM Строительство. Теперь перейдем к более сложным техникам, используя векторные функции и ограничения перемещения «ручек» для управления сложными геометрическими формами.
Ограничение перемещения «ручки» положения
Во второй части статьи («САПР и графика» № 4’2025) уже был рассмотрен случай ограничения перемещения «ручки» положения на примере задания координаты Z=0 (рис. 7). А сейчас рассмотрим другие варианты ограничений:
- ограничение перемещения в линейном диапазоне;
- ограничение перемещений на фиксированном радиусе от точки вращения.
Ограничение перемещения в линейном диапазоне
Зададим ограничение перемещения в прямоугольной плоскости на примере отверстия в плите перекрытия.
Вставим в модель плиту перекрытия из базы данных, используя панель узлов и готовых решений (рис. 1).
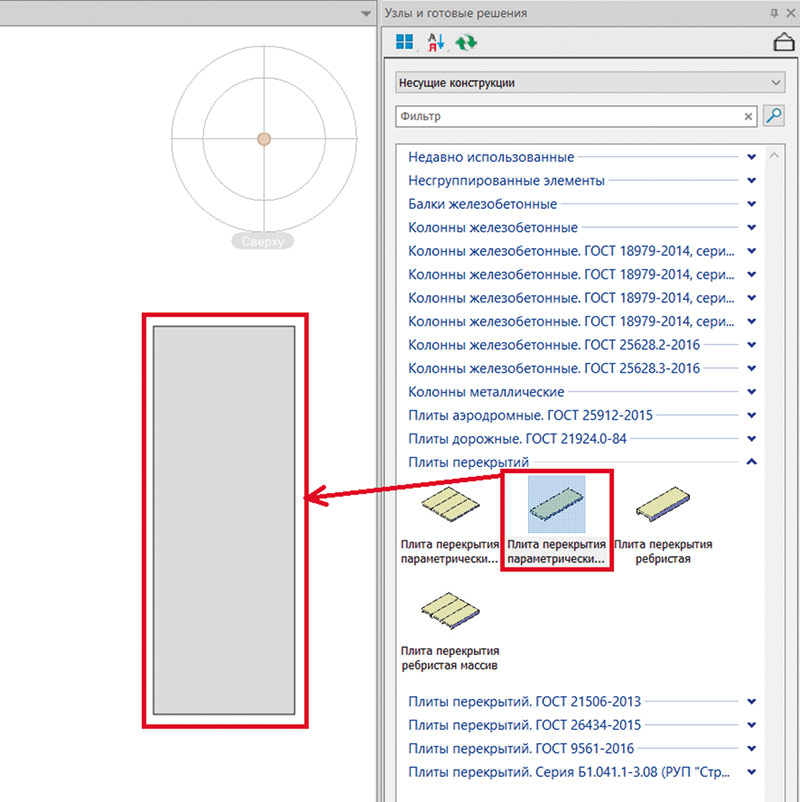
Рис. 1. Вставка плиты перекрытия из базы данных
Откроем плиту перекрытия в окне Редактора параметрического объекта и добавим в нее элемент BOX, который будет вычитать свой объем из плиты (рис. 2 и 3).
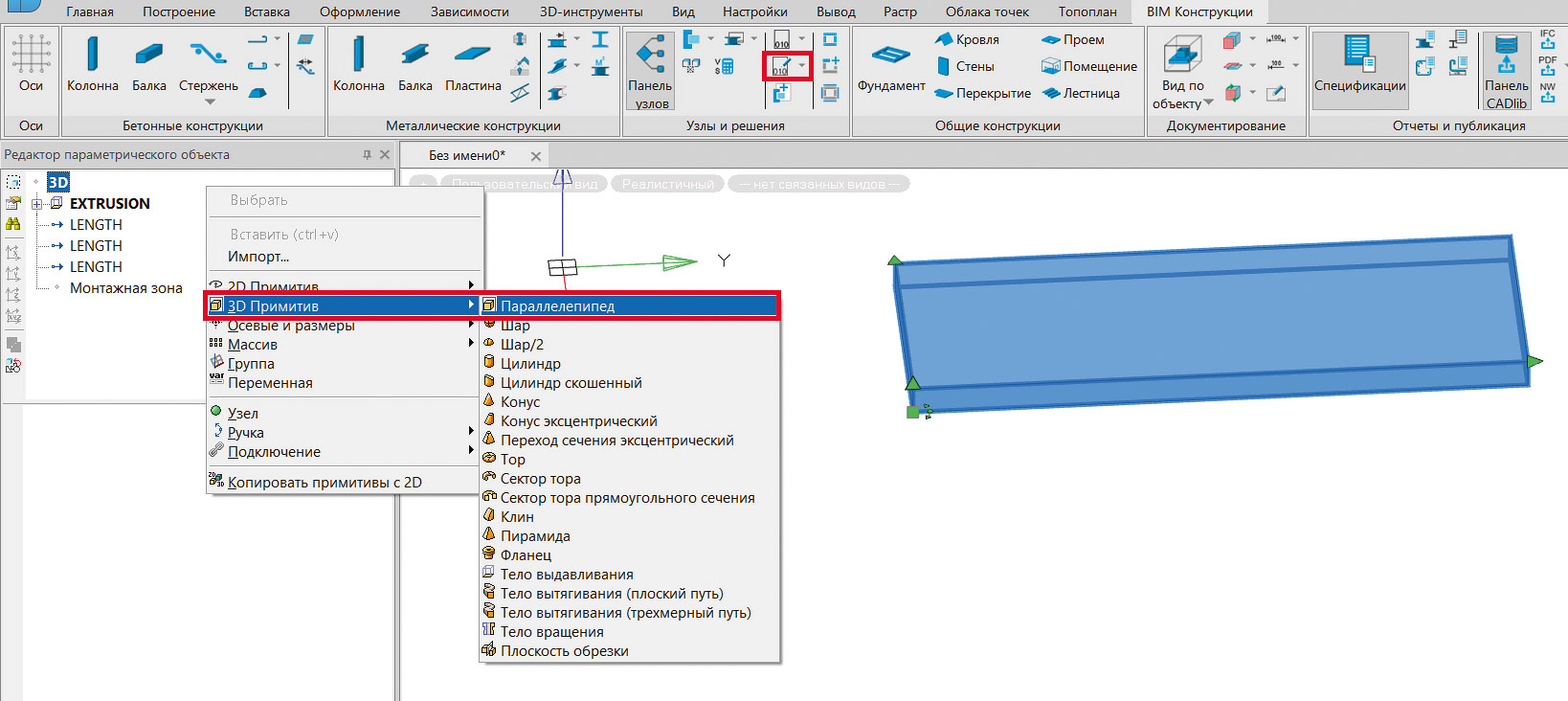
Рис. 2. Добавление BOX в Редакторе параметрического объекта
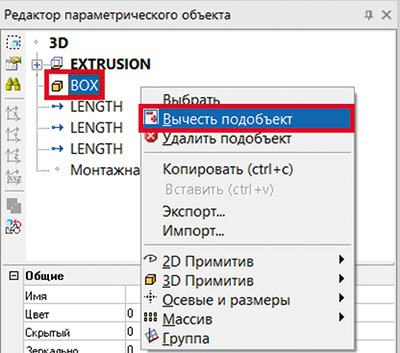
Рис. 3. Вычитание BOX из геометрии плиты
Для перемещения вычитающего BOX добавим «ручку» положения (рис. 4).
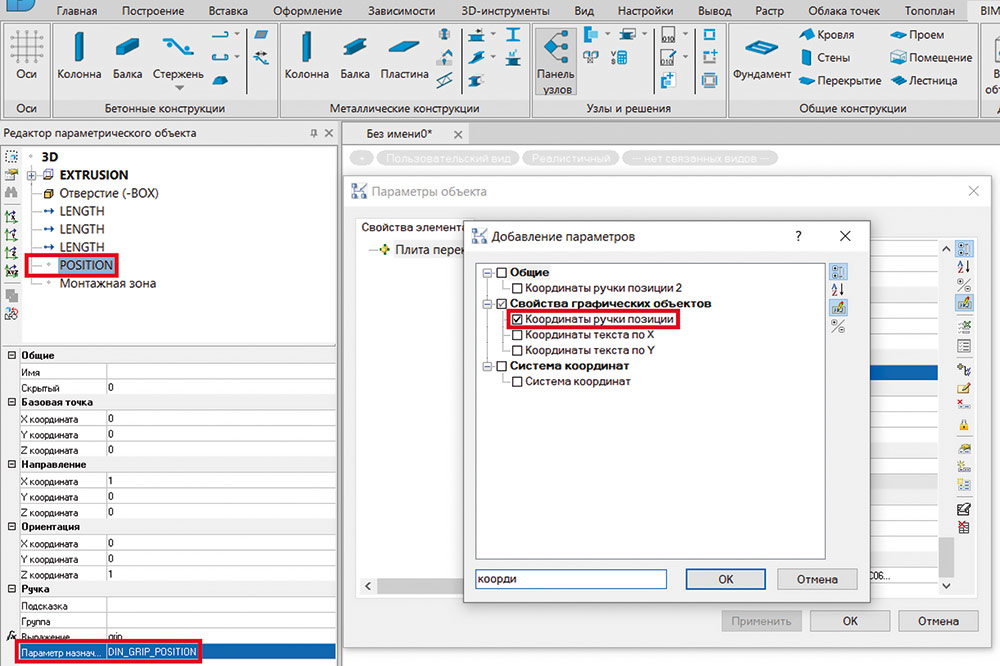
Рис. 4. Создание «ручки» положения BOX
В BOX пропишем соответствующие координаты «ручки» положения (рис. 5).
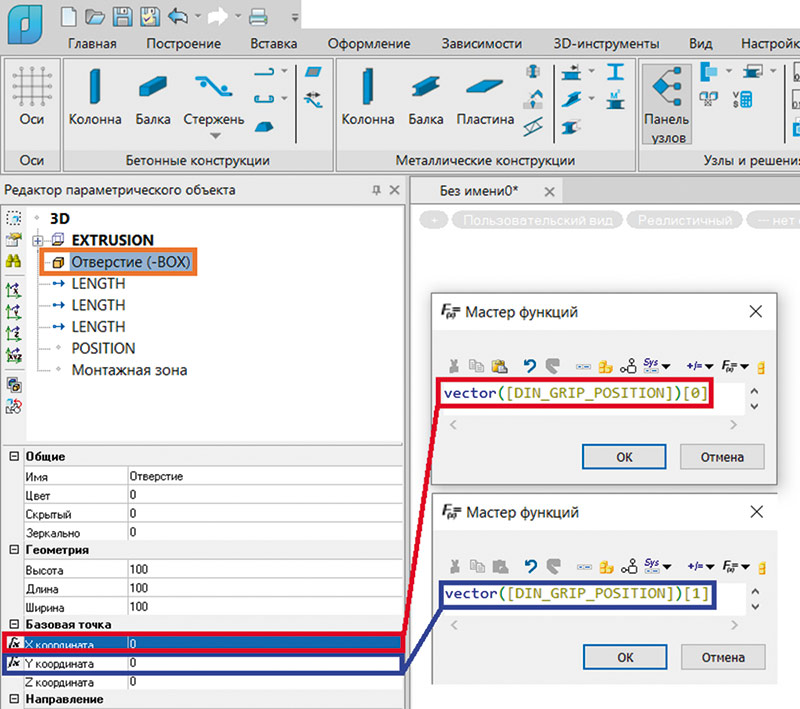
Рис. 5. Параметризация базовой точки BOX при помощи «ручки» положения
Теперь можно перемещать отверстие внутри плиты (рис. 6).
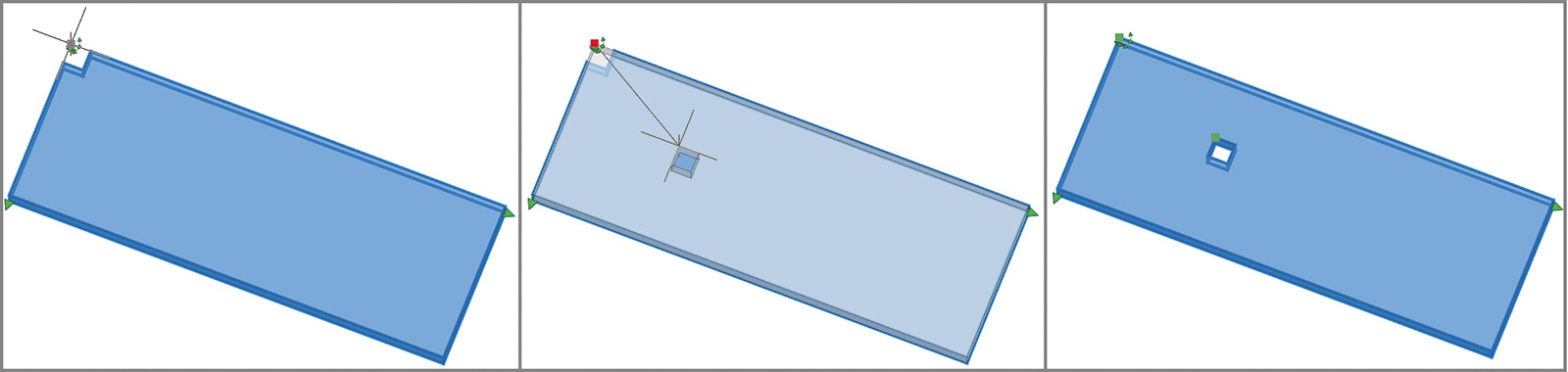
Рис. 6. Перемещение отверстия с помощью «ручки» положения
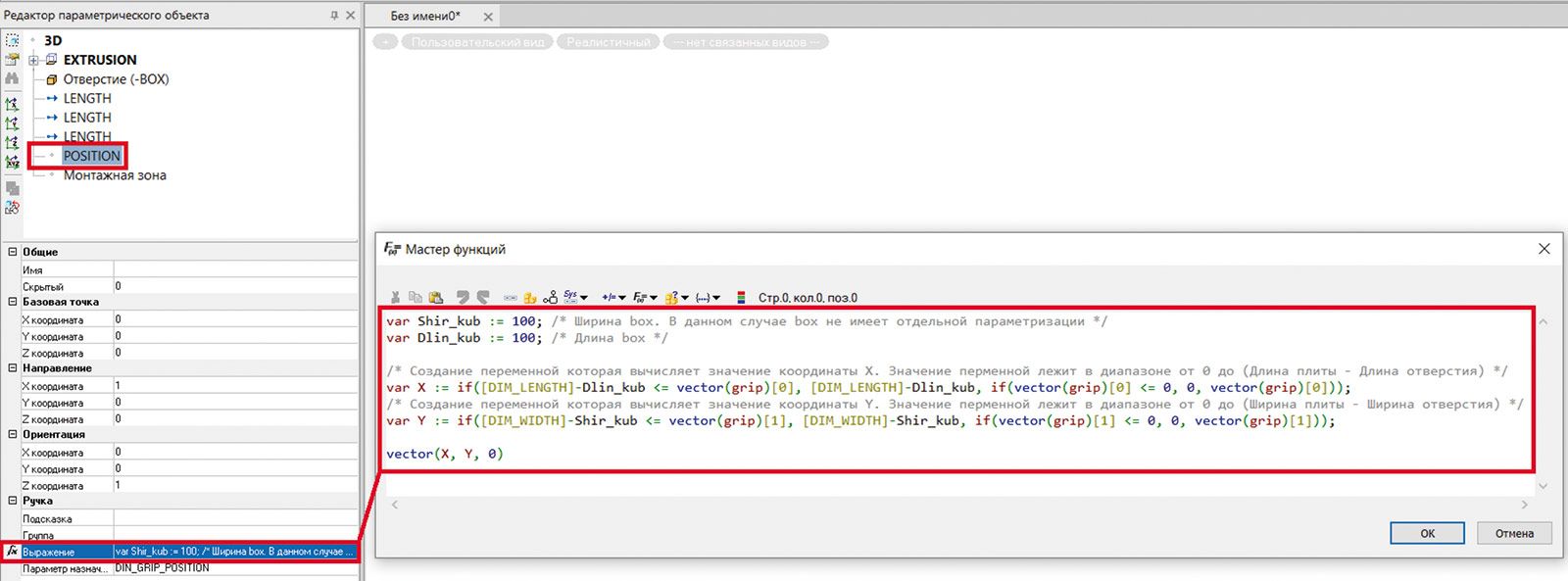
Рис. 7. Параметризация ограничений перемещения «ручки» положения отверстия
Но в такой параметризации не заданы ограничения перемещения, поэтому отверстие может выйти за габариты плиты. Чтобы избежать подобной ситуации, необходимо прописать соответствующую формулу в «ручке» положения в параметре Выражение (рис. 7), где:
- /*...*/ — комментарии в окне Мастера функций;
- var `имя переменной`: = `Формула вычисления значения переменной`; — объявление переменной и присвоение ей значения. Использование переменной внутри окна редактора удобно, если выражение получается слишком длинным либо есть участки с повторяющимся кодом.
По указанной в конце этого предложения ссылке размещено видео, где показано создание объекта: https://disk.yandex.ru/i/jdjEMyuevsiAoA.
А по размещенной в конце этого предложения ссылке можно посмотреть чертеж с готовым объектом: https://disk.yandex.ru/d/BGzqe7IyQB3SQA.
Ограничение перемещений на фиксированном радиусе от точки вращения
В приведенном во второй части статьи на рис. 26 («САПР и графика» № 4’2025) примере показано, как «ручка» положения отрывается от отрезка. Одним из вариантов решения этой проблемы является фиксация «ручки» поворота на каком-то радиусе от точки вращения. Рассмотрим этот вопрос на примере фиксации «ручки» положения в рамках окружности, то есть в случае, когда параметризация выполняется в плоскости. Использование «ручки» положения для такой параметризации избыточно, лучше воспользоваться «ручкой» угла. Но рассмотрение такой параметризации на плоском примере упростит понимание параметризации для случая, если поворот осуществляется в рамках сферы, то есть в трехмерном пространстве.
Выведем формулу, которая рассчитывает координаты точек окружности с радиусом L (рис. 8). Эта окружность описывает возможную траекторию перемещения «ручки».
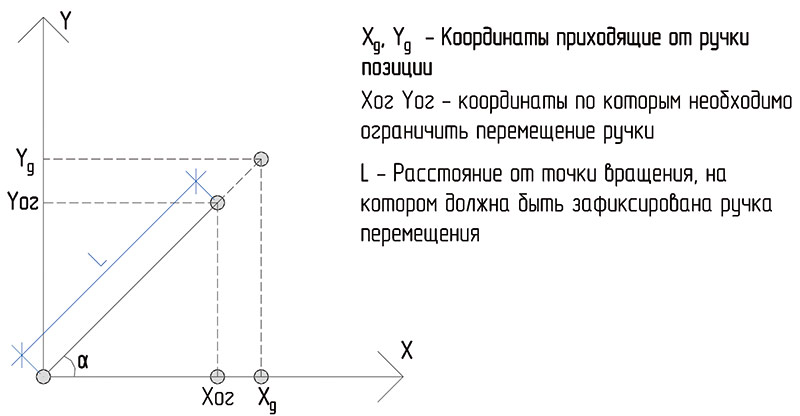
Рис. 8. Проекции имеющихся и искомых координат
Учитывая, что косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе, можно составить формулу:
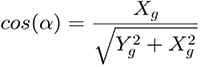
Аналогичную формулу можно представить, выразив косинус угла альфа через Xог и L:
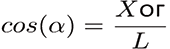
Приравняем правые части уравнений:
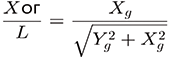
И выразим из полученного равенства Xог:
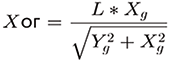
Аналогичная формула получится и для Yог с той лишь разницей, что выражать надо будет через синус угла альфа.
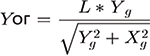
Вернемся к предыдущему примеру параметризации ориентации объекта во второй части статьи — рис. 33 (см. «САПР и графика» № 4’2025) и воспользуемся выведенными формулами. Пропишем формулы в поле Выражение «ручки» положения, которая задает ориентацию группы с отрезками (рис. 9). Радиус L, на котором зафиксируем «ручку» положения, примем равным 100.
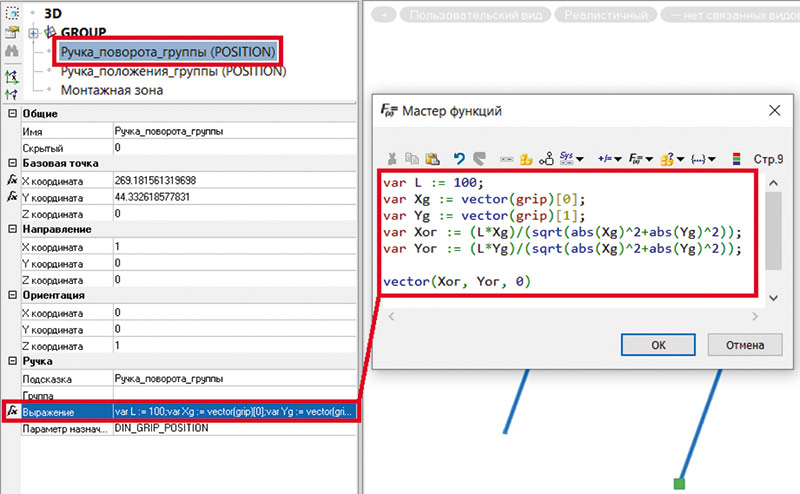
Рис. 9. Параметризация ограничения перемещения «ручки» положения в рамках окружности
Таким образом, независимо от точки пространства, где будет установлена «ручка», она всегда будет на расстоянии L от точки вращения (рис. 10).
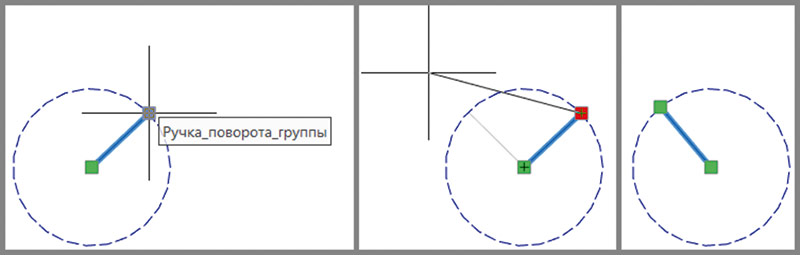
Рис. 10. Демонстрация ограничений перемещения «ручки» положения
В конце этого предложения размещена ссылка на видео, в котором это показано: https://disk.yandex.ru/i/8FYHa3jaCPyOaw.
А это ссылка на чертеж с объектом: https://disk.yandex.ru/d/UErvrS-MkVZEHw.
Формулы для ограничения перемещения «ручки» в рамках сферы выглядят аналогичным образом.
Вывод формулы для косинусов соответствующих углов приведен по ссылке: https://scask.ru/j_dict_math.php?id=103.
Учитывая, что формулы выглядят аналогичным образом, потребуется лишь немного изменить содержание, ранее прописанное в поле Выражение (рис. 11).
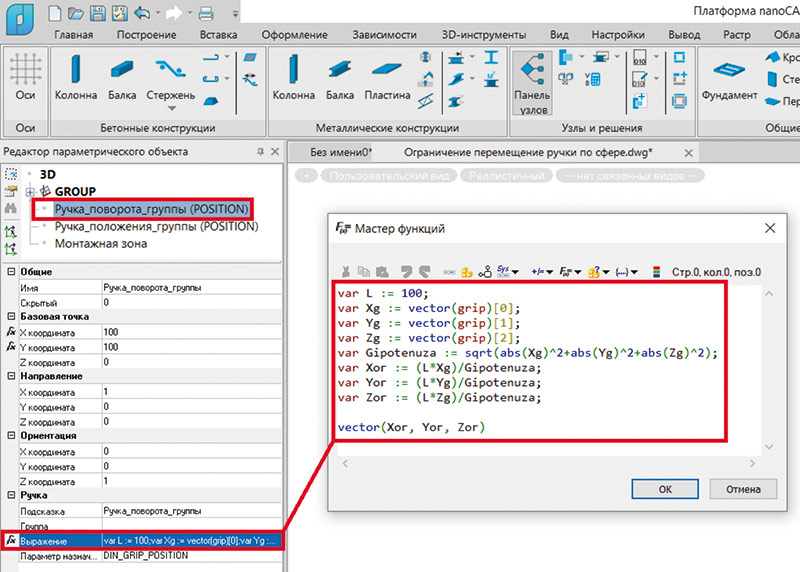
Рис. 11. Параметризация ограничения перемещения «ручки» положения в рамках сферы
Теперь «ручка» положения может перемещаться и по координате Z. Учитывая это, необходимо дополнить имеющуюся параметризацию векторов направления и ориентации. В этом случае группа сможет вращаться по трем осям относительно начала своих координат (рис. 12).
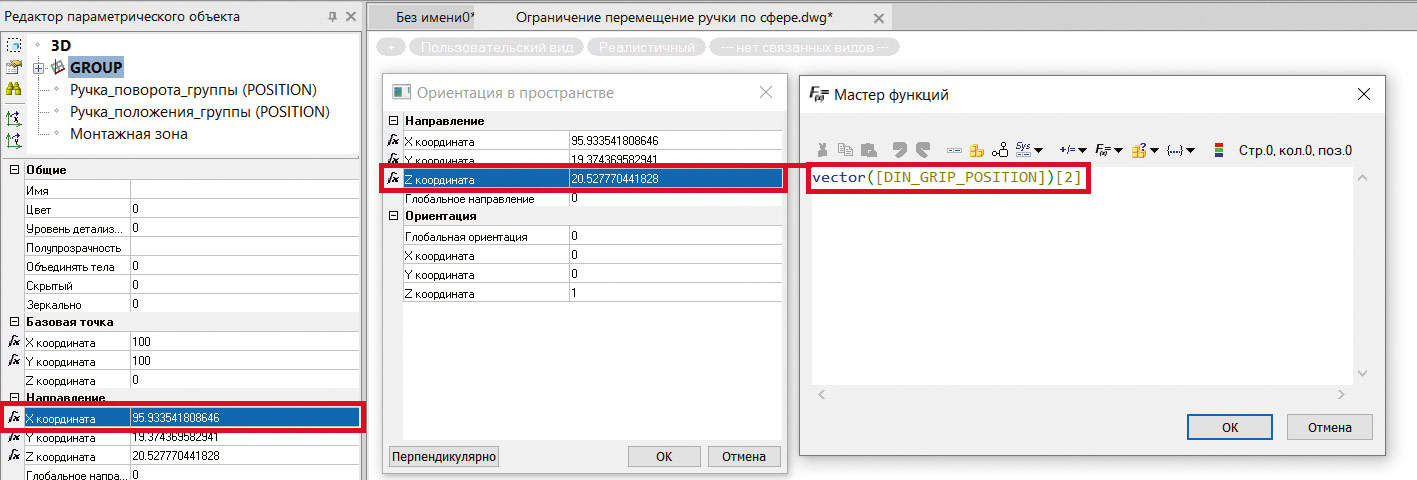
Рис. 12. Дополнение к параметризации вектора направления
В случае, если координата Z не равна нулю, как показано на скриншоте выше, то при нажатии кнопки ОК в окне Ориентация в пространстве на экране появится сообщение Вектор Direction не перпендикулярен вектору Orientation! (рис. 13).
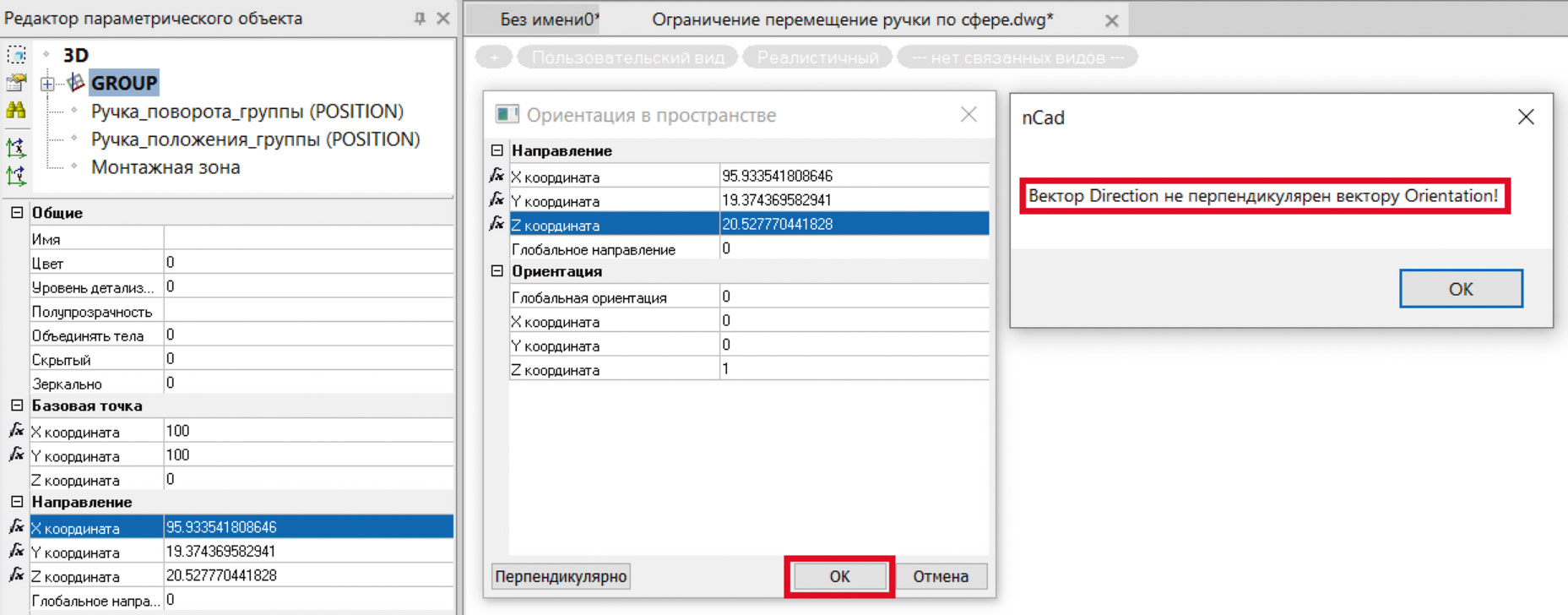
Рис. 13. Ошибка неперпендикулярности векторов направления и ориентации
Связано это с тем, что при таких координатах векторы направления и ориентации не перпендикулярны друг другу. Чтобы обеспечить условие перпендикулярности, необходимо выбрать какую-либо координату вектора, который должен стать перпендикулярным, в данном случае вектора ориентации, и после этого нажать кнопку Перпендикулярно. Новые координаты будут прописаны в векторе. Можно нажать кнопку ОК, ошибка возникать уже не будет (рис. 14).
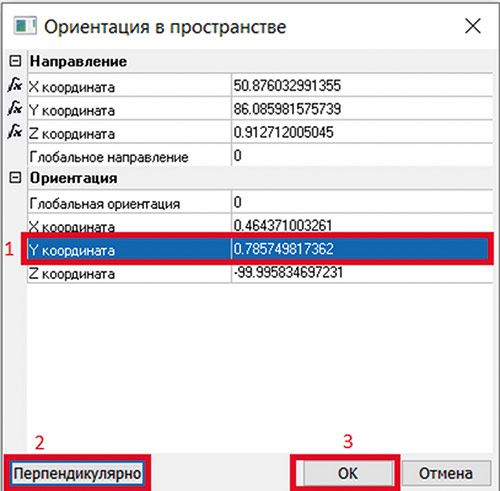
Рис. 14. Параметризация перпендикулярности второго вектора
Теперь с помощью «ручки» положения группу можно вращать по трем осям — XYZ.
Но кое-что еще надо поправить дополнительно. Ранее длина отрезков группы вычислялась для плоского варианта, теперь же необходимо добавить координату Z (рис. 15).
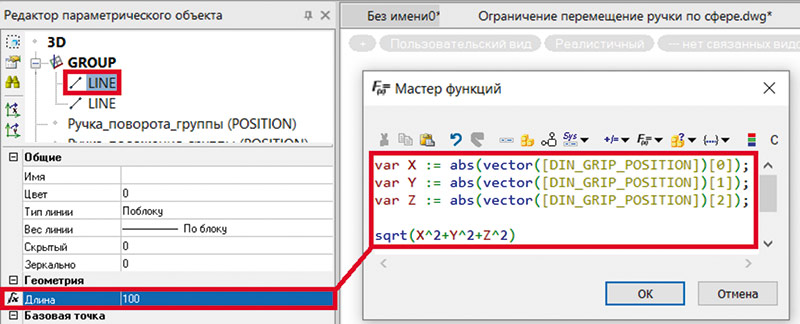
Рис. 15. Параметризация длины отрезков с учетом координаты Z
Далее дана ссылка на видео с демонстрацией: https://disk.yandex.ru/i/mzybvzBwKX-Gjw.
А вот ссылка на чертеж с объектом: https://disk.yandex.ru/d/6HMqqZ4CMgKnYQ.
Вычисление точки пересечения прямых на плоскости
При параметризации геометрии может возникнуть потребность в нахождении точки пересечения отрезков или прямых, например, если в точке пересечения необходимо отрисовать какую-либо геометрию. В базе оборудования есть пример такого объекта. Его можно найти на панели узлов в категории Ограждающие конструкции (рис. 16).
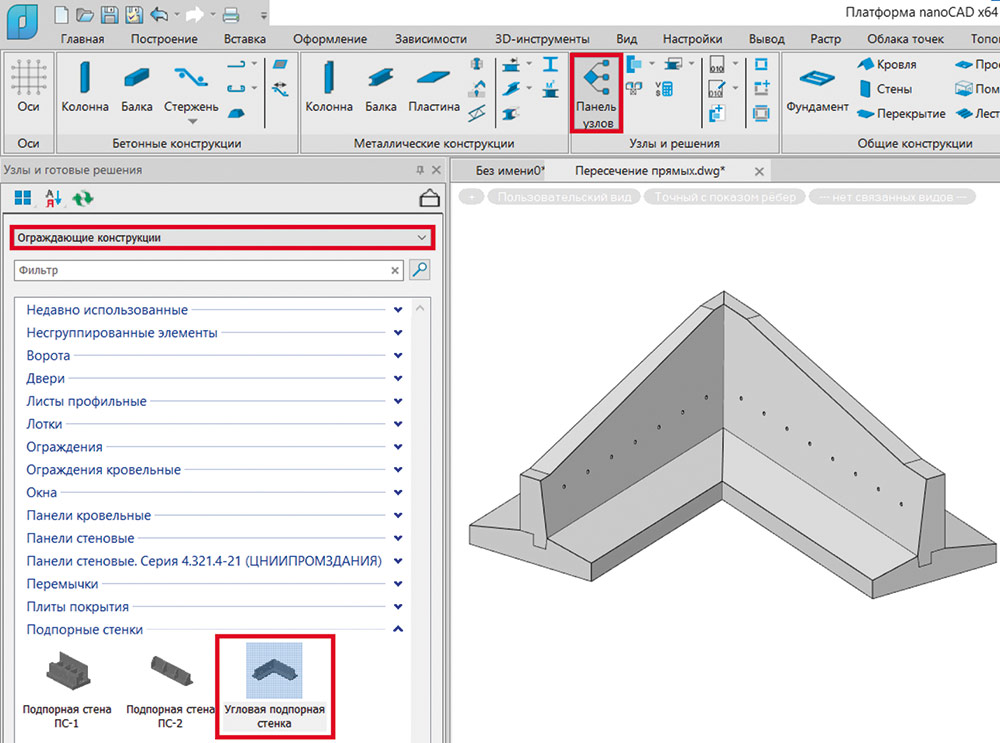
Рис. 16. Пример объекта с параметризацией по пересечению прямых
В ходе создания этого параметрического объекта для параметризации высоты стены в точке пересечения сегментов необходимо будет найти эту точку. Рассчитанная точка пересечения, в свою очередь, будет необходима для параметризации базовой точки «ручки» длины (рис. 17).
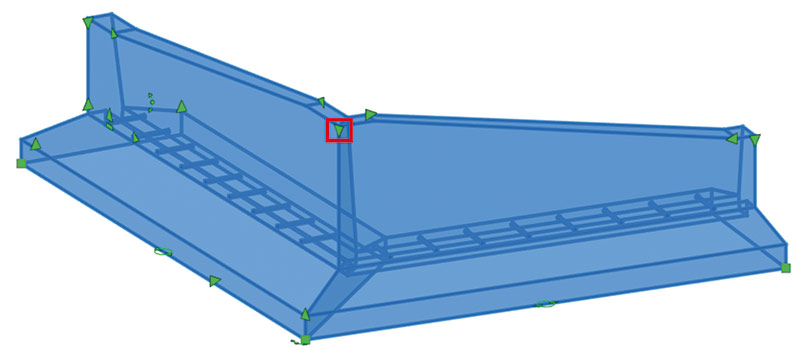
Рис. 17. Параметризация «ручки» длины в точке пересечения
Целиком воспроизводить этот объект здесь нет необходимости. Поэтому разберем теорию вопроса, а практический пример будет обобщенным. В качестве примера создадим объект с двумя отрезками, для которых положение точек начала и конца будет задаваться «ручками» положения. А на пересечении линий отрезков будет отрисовываться цилиндр.
Создадим новый объект и добавим в него два отрезка по двум точкам (рис. 18).
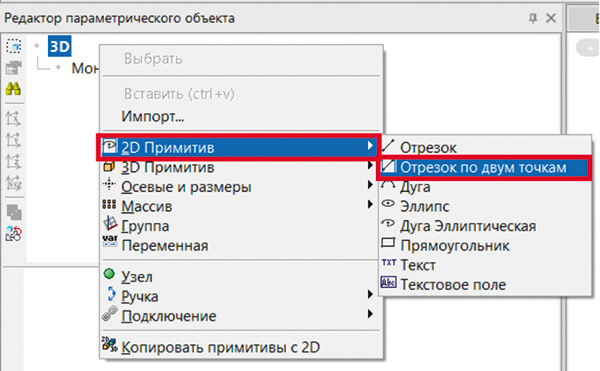
Рис. 18. Добавление отрезков по двум точкам
Также создадим четыре «ручки» положения, которые будут задавать начало и конец отрезков (рис. 19).
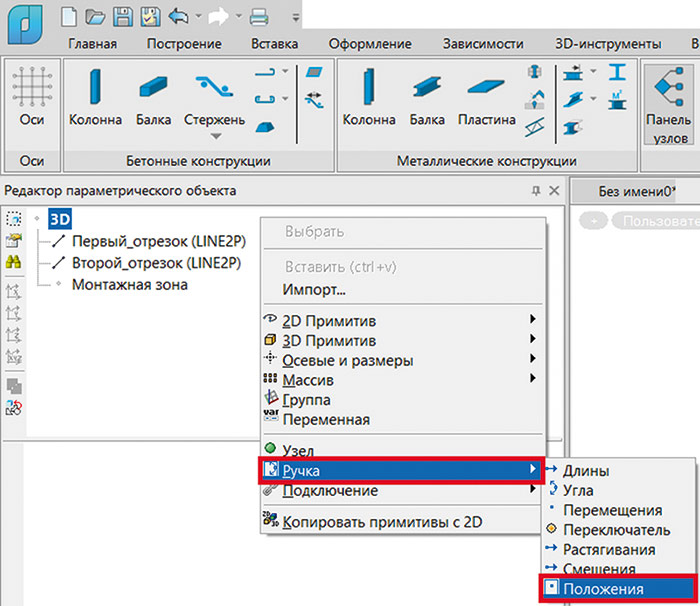
Рис. 19. Добавление четырех «ручек» положения
В свойства объекта добавим четыре новых параметра, которые будут содержать координаты «ручек» положения (рис. 20). Координаты текста не очень подходят по смыслу для этой задачи, но чтобы не добавлять в базу дополнительных параметров, воспользуемся ими.
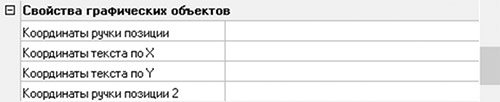
Рис. 20. Добавление параметров с координатами положения «ручек»
- Координаты «ручки» позиции — начало первого отрезка.
- Координаты текста по оси X — конец первого отрезка.
- Координаты «ручки» позиции 2 — начало второго отрезка.
- Координаты текста по оси Y — конец второго отрезка.
Соответствующие имена параметров назначим в поле параметра назначения «ручек» положения (рис. 21).
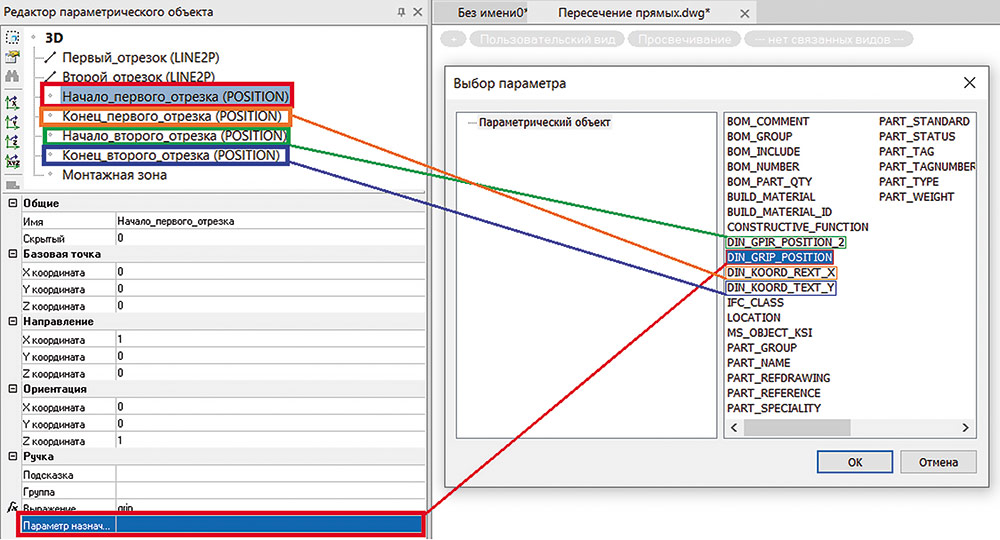
Рис. 21. Назначение параметров «ручек» положения
Учитывая, что задача решается для плоского варианта, также необходимо ограничить перемещение «ручек» положения по координате Z с помощью поля Выражение, как это было сделано ранее в соответствии с рис. 7 (см. часть 2, «САПР и графика» № 4’2025).
В свойствах отрезков пропишем соответствующие выражения для базовой и второй точки (рис. 22).
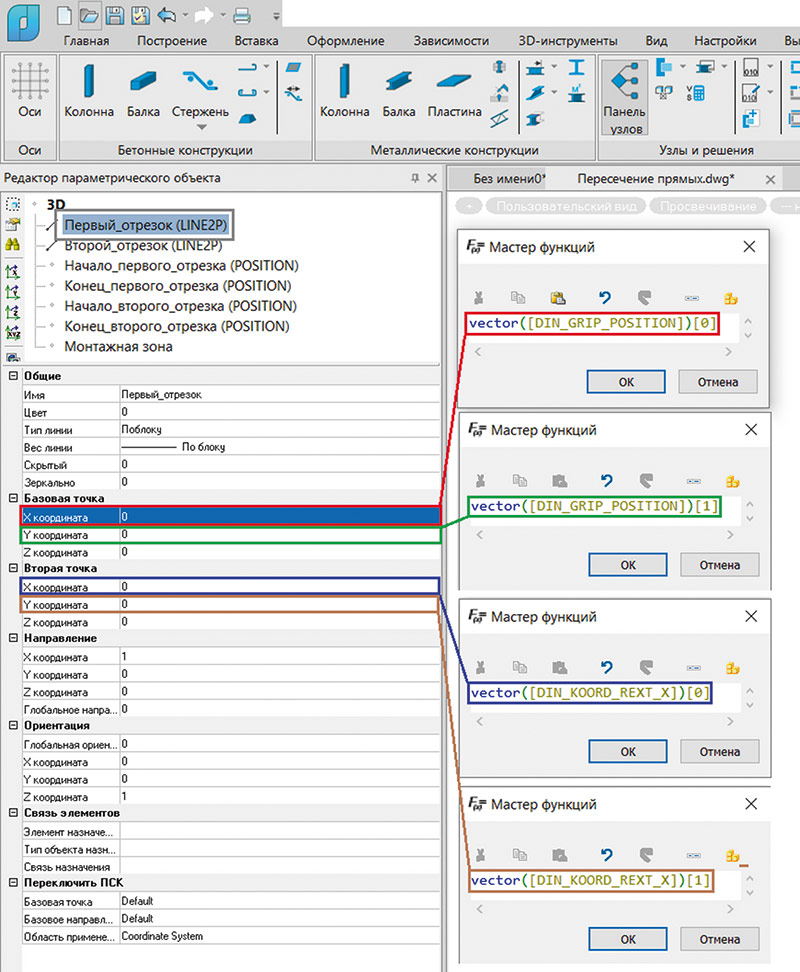
Рис. 22. Параметризация базовой и второй точек отрезков
Существует аналитическое решение, которое позволяет найти точку пересечения двух прямых на плоскости. В сущности, необходимо решить систему из двух уравнений прямых. Для прямых существует множество вариантов записи уравнения прямой. В этой статье рассматривается вариант записи уравнения с коэффициентами (общим уравнением), так как систему таких уравнений довольно легко решать методом Крамера.
Классическое уравнение прямой:
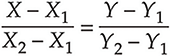
где:
X1, Y1 — точка начала вектора (отрезка), лежащего на прямой;
X2, Y2 — точка конца вектора (отрезка), лежащего на прямой.
В этом случае координаты X1, X2, Y1, Y2 передают «ручки» положения.
Запишем уравнение в одну строку:
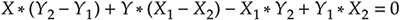
Коэффициенты перед X и Y, а также свободные члены соответственно равняются:
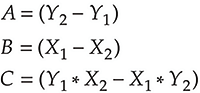
В итоге получается уравнение прямой с коэффициентами (общее уравнение):
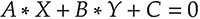
Поиск точки пересечения прямых на плоскости подразумевает решение системы уравнений прямых:
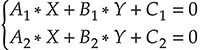
Решим эту систему уравнений методом Крамера. Для этого пропишем соответствующие определители:
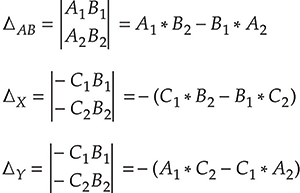
В соответствии с методом Крамера решение системы уравнений выглядит так:
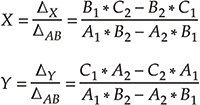
Учитывая, что коэффициенты A, B, C вычисляются по координатам начала и конца отрезков, в Мастере функций можно написать соответствующие выражения.
Добавим переменную в окне Редактора параметрического объекта, чтобы прописать в ней выражение в соответствии с выведенными формулами (рис. 23).
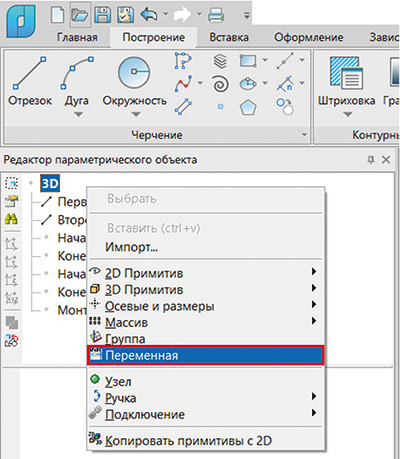
Рис. 23. Добавление переменной в окне Редактора параметрического объекта
Переменной присвоим имя Точка_пересечения (рис. 24).
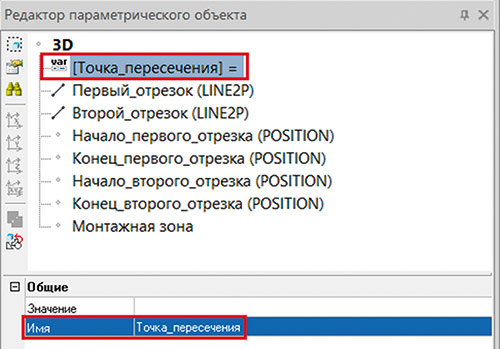
Рис. 24. Присвоение имени переменной
В параметре Значение, воспользовавшись Мастером функций, пропишем выражение в соответствии с ранее выведенными формулами (рис. 25).
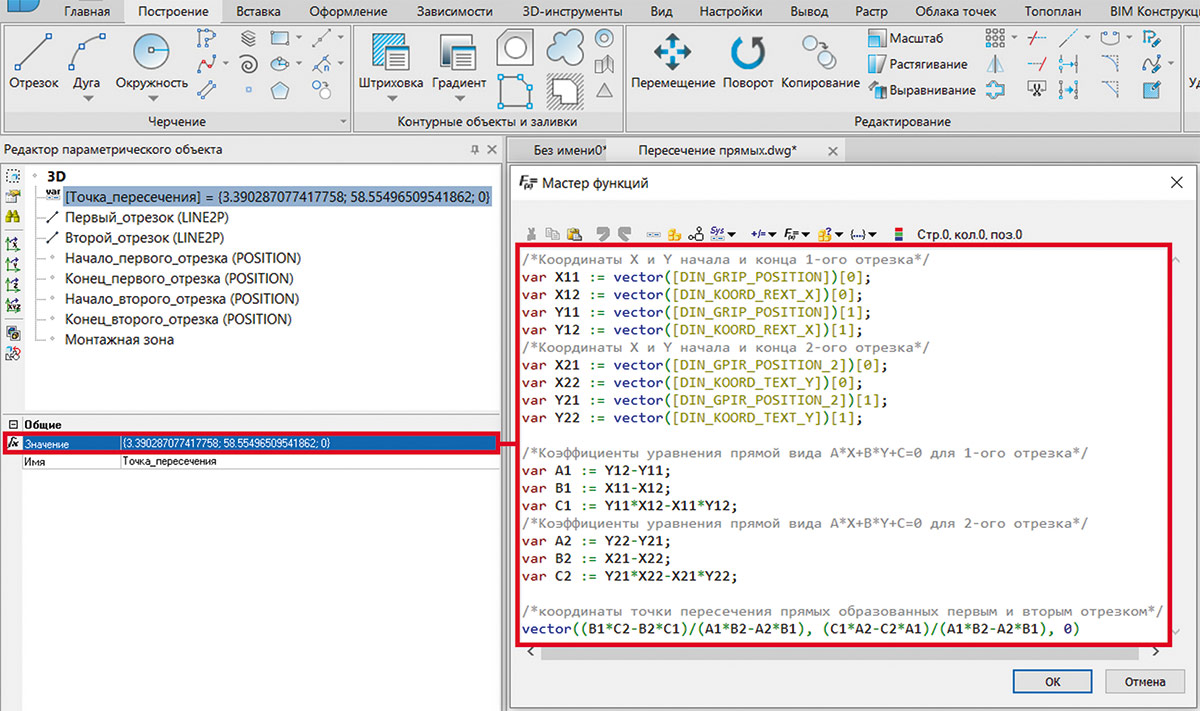
Рис. 25. Выражение, высчитывающее значение точки пересечения отрезков
О компании «Нанософт» «Нанософт» — российский разработчик инженерного ПО: технологий автоматизированного проектирования (CAD/САПР), информационного моделирования (BIM/ТИМ) и сопровождения объектов промышленного и гражданского строительства (ПГС) на всех этапах жизненного цикла, а также сквозной цифровизации всех процессов в производстве. Флагманский продукт — Платформа nanoCAD — универсальная САПР для создания чертежей и 3D-моделей с прямой поддержкой *.dwg-формата (официальный сайт: nanocad.ru). |
О компании «Макссофт-24» ООО «Макссофт-24» — авторизованный партнер крупнейших российских разработчиков программного обеспечения и поставщиков широкоформатного оборудования. Мы являемся Премьер- и Фокус-партнером компании «Нанософт разработка», что подтверждает высокий уровень экспертизы по линейке решений nanoCAD. Мы всегда находимся с разработчиком в прямом контакте для оперативного и компетентного решения ваших задач. Более 30 лет мы занимаемся комплексной интеграцией в инфраструктуру организаций различного масштаба ИТ-решений широкого функционального назначения: общесистемный софт, САПР и ТИМ, информационная безопасность, прикладное ПО, электронный документооборот, ЭЦП (официальный сайт: maxsoft.ru). |
Для наглядности добавим в объект какой-нибудь примитив, например цилиндр (рис. 26).
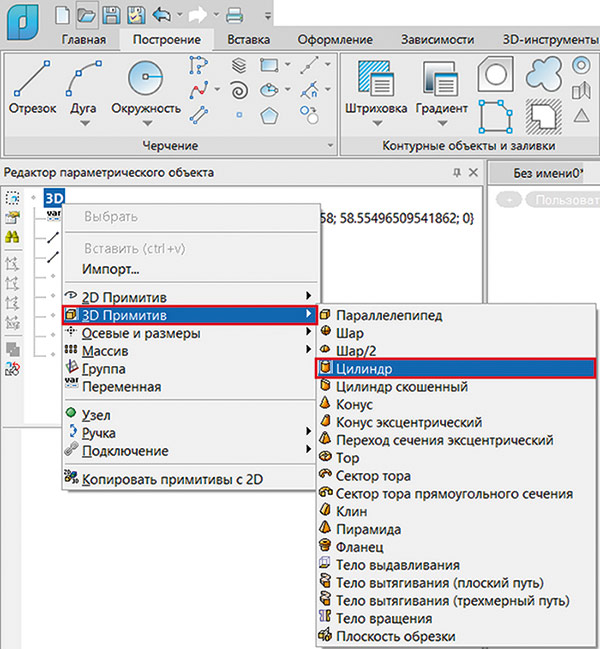
Рис. 26. Добавление цилиндра
В свойствах базовой точки цилиндра пропишем координаты точки пересечения. Чтобы воспользоваться ранее созданной переменной, достаточно написать ее имя в Мастере функций (рис. 27).
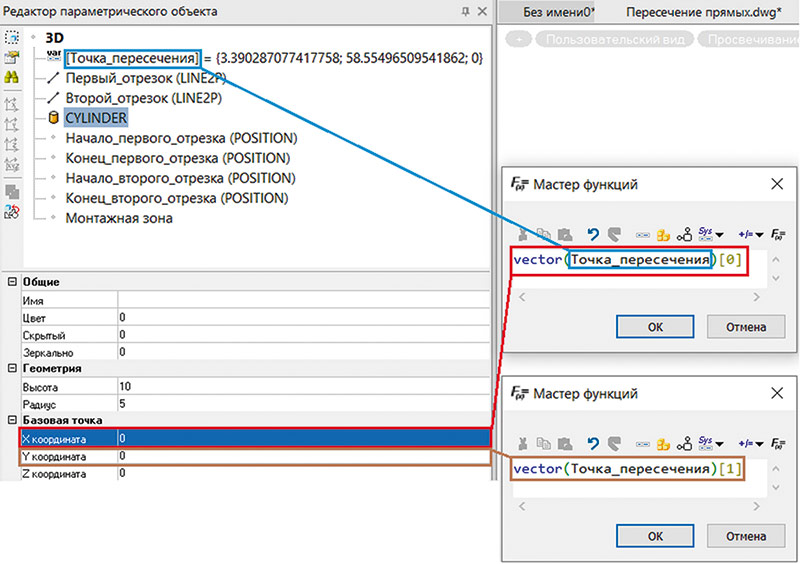
Рис. 27. Использование переменной точки пересечения для параметризации базовой точки цилиндра
Теперь при изменении какой-либо точки положения начала или конца отрезков соответственно меняется положение цилиндра (рис. 28).
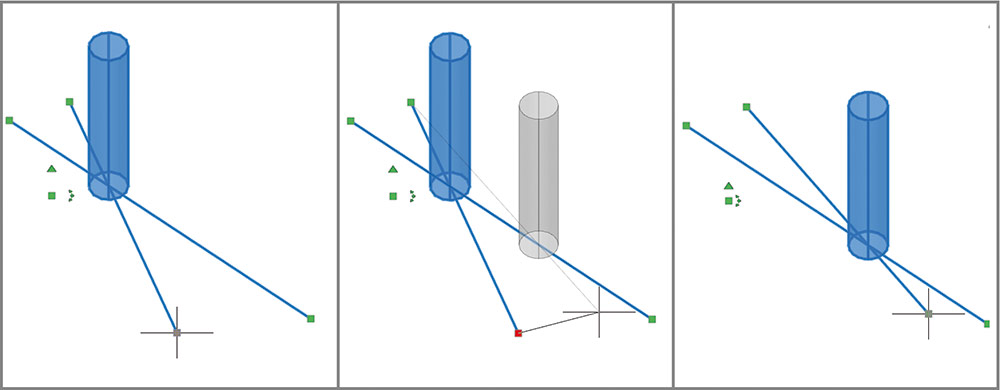
Рис. 28. Параметризация точки пересечения
Демонстрация параметризации представлена в видео по ссылке: www.disk.yandex.ru/i/65vTkiNatBYWbQ.
А здесь дана ссылка на чертеж с объектом: www.disk.yandex.ru/d/SH2icMkux-X3Lg.
***
Описанные приемы параметризации позволяют существенно расширить возможности применения параметрических объектов и nanoCAD BIM Строительство (конфигурация «Конструкции»).
Обладая знаниями о параметризации точек в пространстве, можно создавать объекты со сложными взаимосвязями геометрических элементов. Описанные в этой статье примеры помогут в полной мере овладеть навыками по созданию такой параметризации.



