Приближается релиз новой версии отечественного геометрического ядра RGK от «Топ Системы». Компания делится результатами работы команды разработчиков, полученными за период, прошедший с предыдущей публикации (САПР и графика, № 7’2024). Была проделана большая и разноплановая работа. Улучшения касались как функциональности API-ядра, так и внутренних базовых алгоритмов. В статье хочется остановиться не только на новой функциональности ядра, но и на важных внутренних улучшениях и алгоритмах, которым в значительной степени была посвящена разработка за прошедший год.
«Неприятные» задачи в геометрическом моделировании
Для того чтобы обсуждать достижения в некоторых аспектах функциональности ядра, нужно поговорить о том, какие задачи являются традиционно трудными и «неприятными» для геометрических ядер. Обычно о таких аспектах в обзорных публикациях говорить не принято, но нам кажется, что для читателей будет полезно более полно понять внутреннюю «кухню» разработки промышленных геометрических ядер, сложности и вызовы, которые возникают в этом процессе. Как известно из предыдущих публикаций, важной особенностью ядра RGK является поддержка точностей топологических элементов и управление этими точностями. В том или ином виде такого рода информация присутствует во всех промышленных ядрах, хотя и в разных формах. Тут важно понимать, что механизм точностей должен являться базовым архитектурным элементом всего ядра, и все алгоритмы ядра должны поддерживать адекватную работу с этой важной информацией. В этом смысле невозможно адекватно внедрить данный механизм в код, который изначально не проектировался с учетом проблем, возникающих в связи со «сквозным» управлением точностью вычислений. На первый взгляд, наличие точностей у ребер и вершин кажется очень простой идеей — любой инженер прекрасно понимает, что в реальности размеры не бывают точными. Но в геометрическом моделировании механизм точностей — это несколько более глубокая вещь. Именно правильная архитектура алгоритмов с учетом точностей является основой для обеспечения надежности геометрического ядра на реальных промышленных данных. Основываясь на многолетнем опыте использования промышленных геометрических ядер и опыте собственных разработок, мы утверждаем, что невозможно обеспечить стабильную работу алгоритмов геометрического ядра без тонкой настройки алгоритмов по управлению точностью. Такие рассуждения могут показаться несколько абстрактными, но они объясняют, почему разработчики RGK так много сил и времени уделяют совершенствованию именно этого аспекта ядра, хотя формально такая работа и не расширяет API. Излишне говорить, что архитектурная поддержка тех или иных аспектов моделирования представляет собой не более чем необходимое условие успеха алгоритмов в обработке сложных и неприятных конфигураций при моделировании. Поэтому процесс совершенствования и выстраивания логики работы ядра в нетривиальных случаях идет постоянно и будет продолжаться в будущих версиях. Итак, какие задачи традиционно считаются «неприятными» в геометрическом моделировании? Это в первую очередь задачи, возникающие при построении пересечений касательных и «почти» касательных поверхностей и кривых. Они возникают в разных алгоритмах ядра — не только как чисто геометрических, но и топологических. Бывают ситуации, когда пересечение в некоторой области с заданной точностью становится двумерным множеством. То есть любая кривая в такой области удовлетворяет заданному условию. Но все дело в том, что с точки зрения конечного результата требуется выбрать только одно решение. То есть доопределить решение плохо обусловленной задачи в математическом смысле. Как следствие, из подобных ситуаций возникает понимание «неприятных» задач, которые не могут быть решены с произвольной точностью в силу особенностей своей постановки. Техника обработки подобных ситуаций зависит как от основного алгоритма моделирования, будь то булева операция, построение сглаживания, уклона и прочее, так и от типов уравнений, задающих геометрию кривых и поверхностей — для аналитических логика и точность обработки могут быть одни, а для сплайновой геометрии — другие. Рассмотрим на примерах, какие результаты получены в новом релизе. Начнем с примеров в булевых операциях (рис. 1 и 2).

Рис. 1. Задача вычитания «трубки» из тела с прорезями. Особенность задачи в том, что геометрия «трубки» почти касается прорезей первого операнда. При этом требуемая точность результата задается генератору в качестве входного параметра
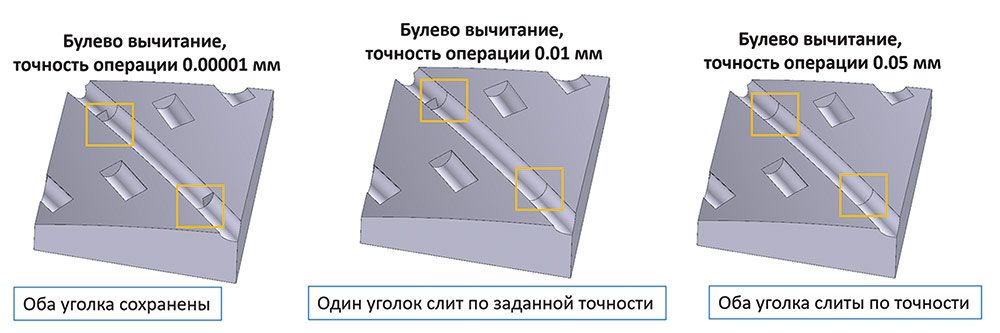
Рис. 2. Результат булева вычитания в зависимости от точности входных данных и требуемой точности операции, заданной как входной параметр
Рассмотрим более подробно поведение алгоритмов ядра в такой ситуации, чтобы пояснить суть происходящего «под капотом». Возьмем один из «уголков» из приведенных выше рисунков и приблизим его. Вот что мы видим, так сказать, «под микроскопом» (рис. 3).
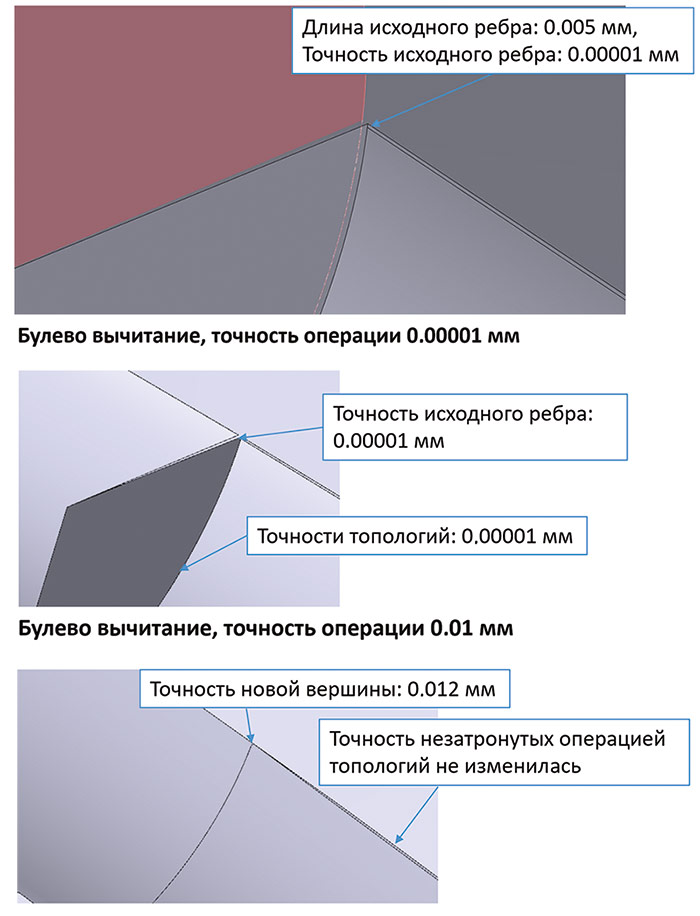
Рис. 3. Подробное рассмотрение зависимости топологического ответа ядра от точности входной модели и точности операции
В приведенной на рис. 3 иллюстрации производится совместный учет точностей в булевой операции:
- учет точности операции при слиянии поверхностей;
- учет точностей ребер и вершин исходных тел;
- слияние вершин и удаление ребер для получения корректного результирующего тела.
Еще пара примеров на эту тему. Рассмотрим вот такое булево вычитание (рис. 4).
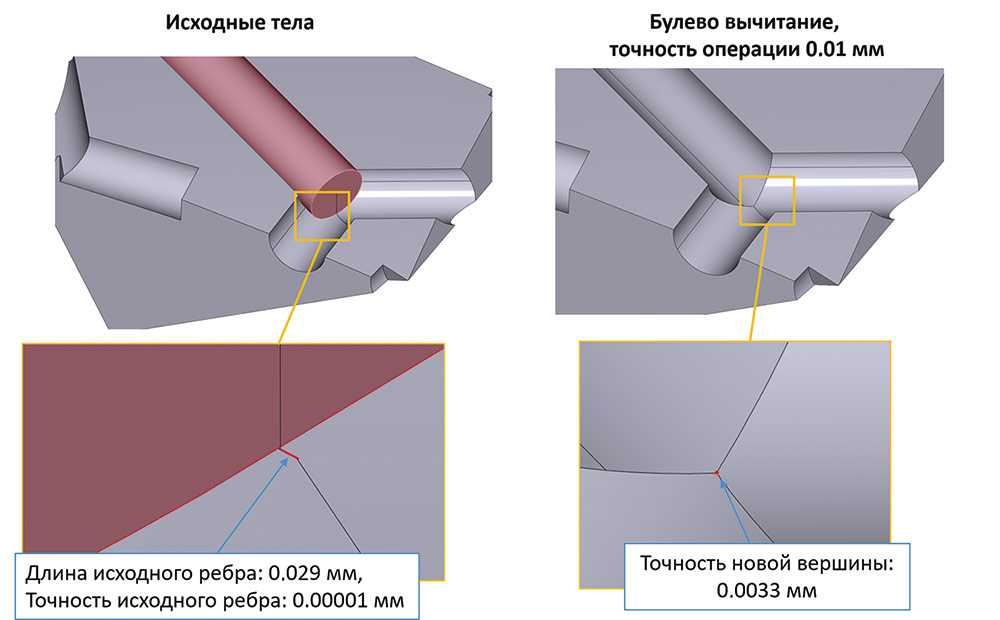
Рис. 4. Учет точностей в булевой операции: слияние вершин и удаление микроребер для построения корректного тела
Еще более непросто обстоит дело с пересечением сплайновых поверхностей. Рассмотрим задачу объединения почти касательных тел со сплайновой геометрией (рис. 5).
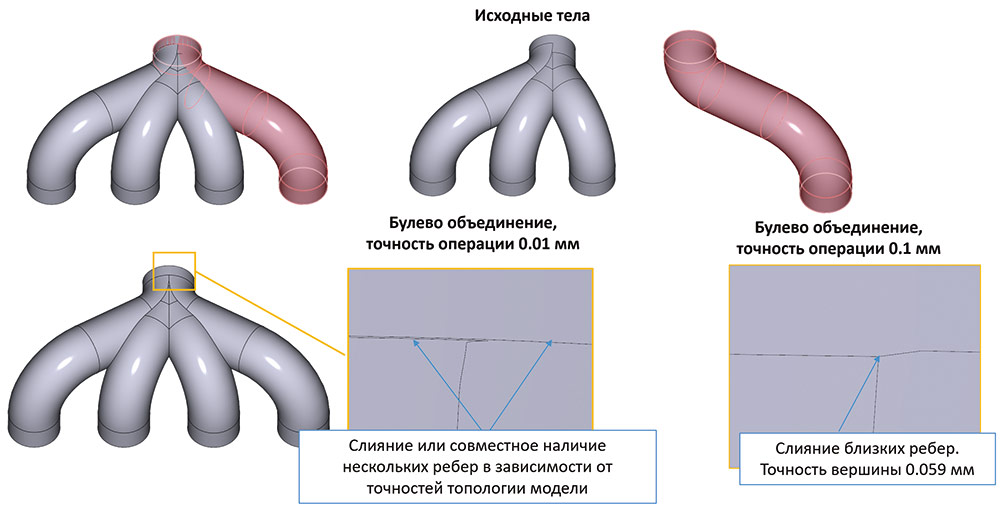
Рис. 5. Пример, показывающий работу RGK в случае частичного наложения сплайновых поверхностей в булевых операциях
Следует отметить, что главную сложность в настройке алгоритмов при работе с толерантными моделями представляет выстраивание единой и непротиворечивой логики поведения всех алгоритмов ядра при различных комбинациях геометрии, топологии и точностей как исходных данных, так и вычислительных алгоритмов получения новой геометрии. В принципе, можно утверждать, что именно наличие такой разработанной и внедренной идеологии и функциональности отличает промышленное ядро от функционального прототипа.
Конечно, развитие геометрического ядра «в глубину» не заменяет его развитие «в ширину», а именно неуклонное наращивание функциональности API в плане как развития уже существовавших генераторов, так и разработки новой функциональности.
Функциональность по формированию и редактированию модели
Логическое развитие получила функциональность генераторов тел по траектории. Теперь в генераторах Sweep, Extrusion и Rotation поддерживается возможность задания толщины стенки результирующего тела (рис. 6).
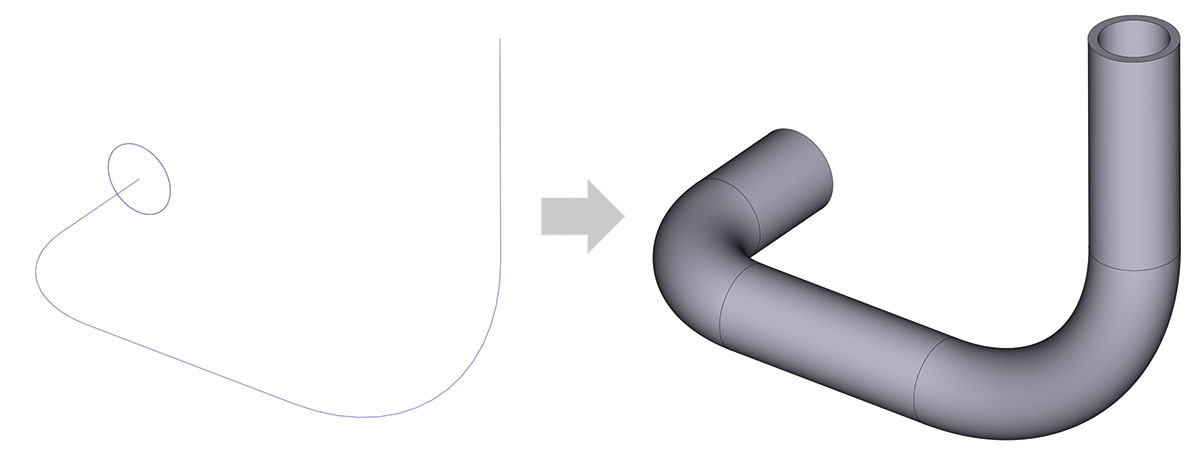
Рис. 6. Придание толщины телу при движении контура по траектории
Возможно придание толщины как в одну сторону (внутрь и наружу контура), так и в обе стороны на разную величину. Стоит напомнить также, что перемещаемый контур может лежать на произвольной поверхности.
Расширилась «интеллектуальность» генерации. В частности, при движении по винтовой и «квазивинтовой» траектории стало доступно три режима ориентации перемещаемого профиля (рис. 7).
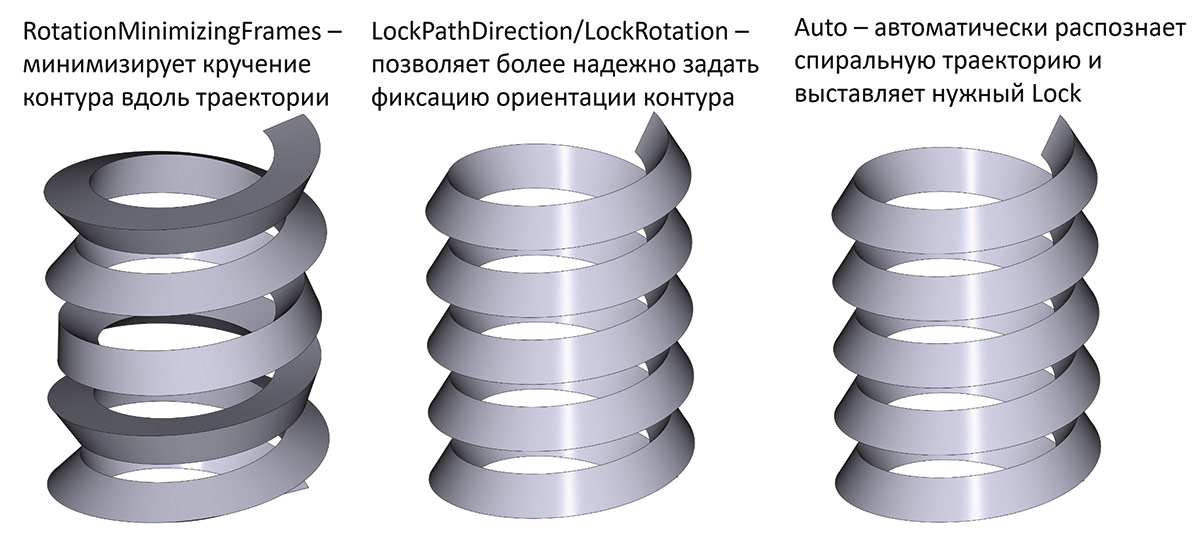
Рис. 7. Режимы ориентации профиля при движении по траектории, похожей на винтовую линию
Следует отметить режим автоматического распознавания винтовой линии — он позволяет создавать «правильно» ориентированные тела не только в случае строго винтовой траектории, но и при траектории, в определенном интуитивном смысле подобной винтовой. Сходным образом ведут себя генераторы геометрии в некоторых других промышленных ядрах. Как говорится, все дело в деталях, и это одна из таких деталей.
В новой версии добавлена поддержка продления многопрофильного тела по траектории за пределы первого и последнего профиля/контура (рис. 8).

Рис. 8. Пример продления многопрофильного тела по траектории за граничные профили: заданы два профиля и траектория, а в качестве полученного результата — тело, которое полностью содержит траекторию и интерполирует заданные профили
Любопытной возможностью является функциональность, поддерживающая несвязные контуры в многопрофильном теле по траектории (рис. 9 и 10).
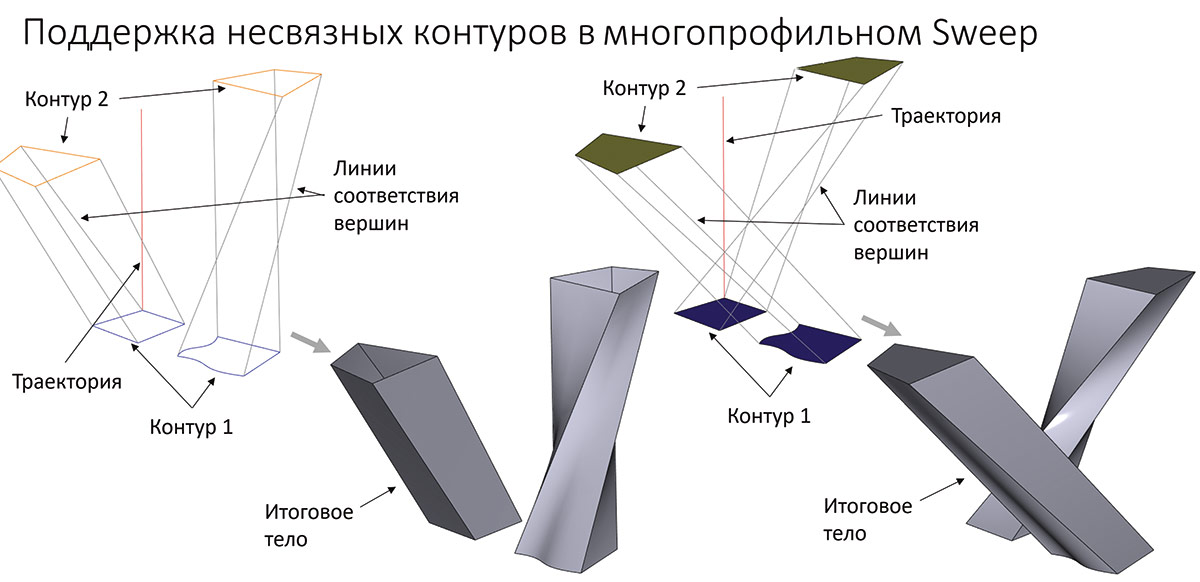
Рис. 9. Построение многопрофильного многосвязного тела по траектории с заданием соответствия компонент связности
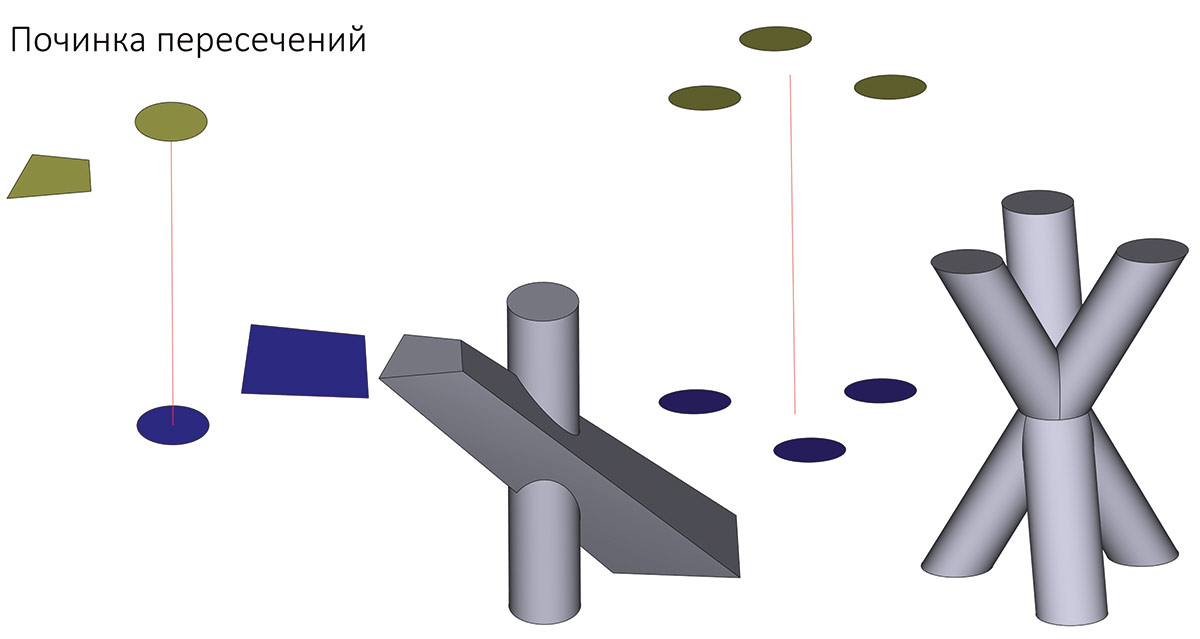
Рис. 10. Построение многосвязного многопрофильного тела по траектории с опцией объединения компонент результата
Кроме того, важно отметить, что эта функциональность допускает использование как замкнутых, так и разомкнутых контуров в качестве компонент связности.
В генераторе «По сечениям»:
- существенно доработан генератор;
- некоторые алгоритмы стали проще и надежнее;
- выросла стабильность и качество результатов;
- добавлена новая функциональность.
Теперь поддерживается комбинация замкнутого и открытого сечения в общем виде (рис. 11).
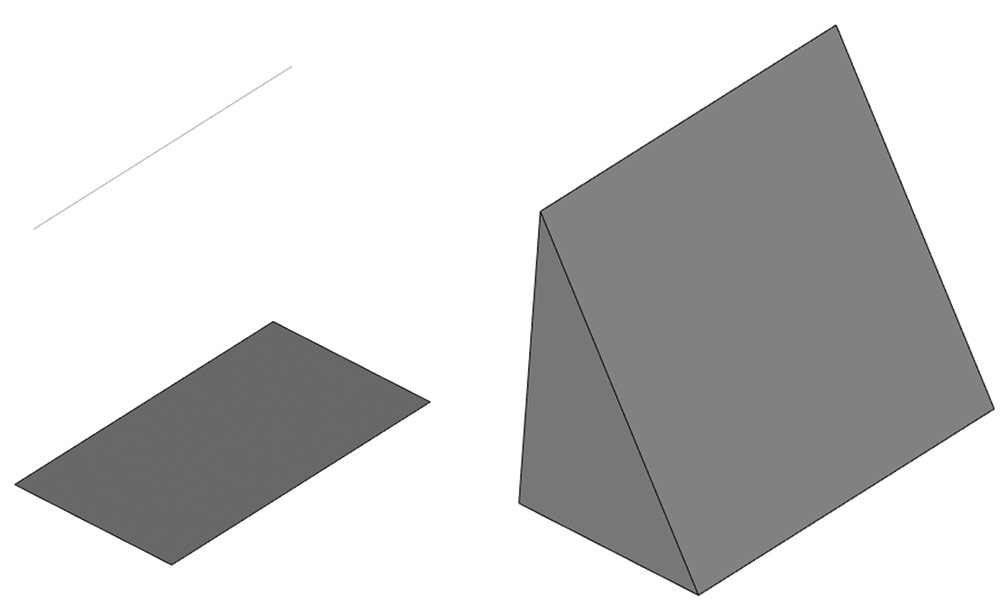
Рис. 11. Комбинация разных типов сечений в операции «По сечениям»
Добавлена поддержка касания сечений по вершинам (рис. 12).
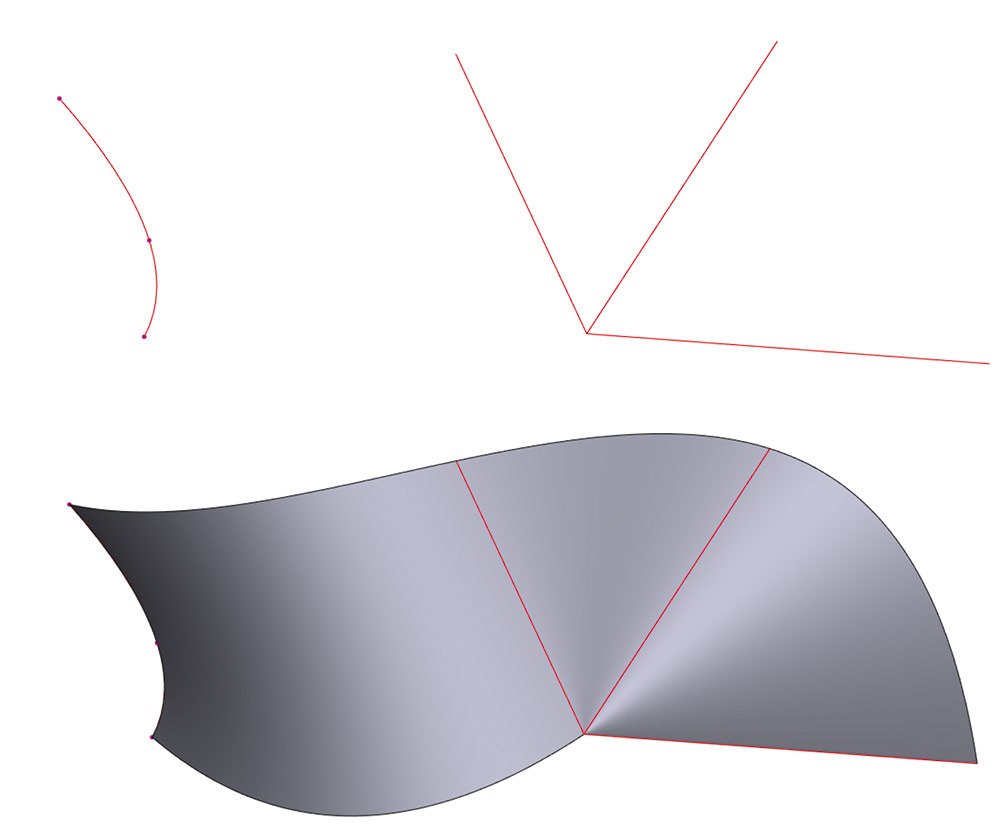
Рис. 12. Пример на касание нескольких сечений по вершине
Реализована поддержка касательных граничных условий в операции «По сечениям» с вершиной — можно задать нормаль плоскости касательной, к которой будет поверхность в точке завершения (рис. 13).
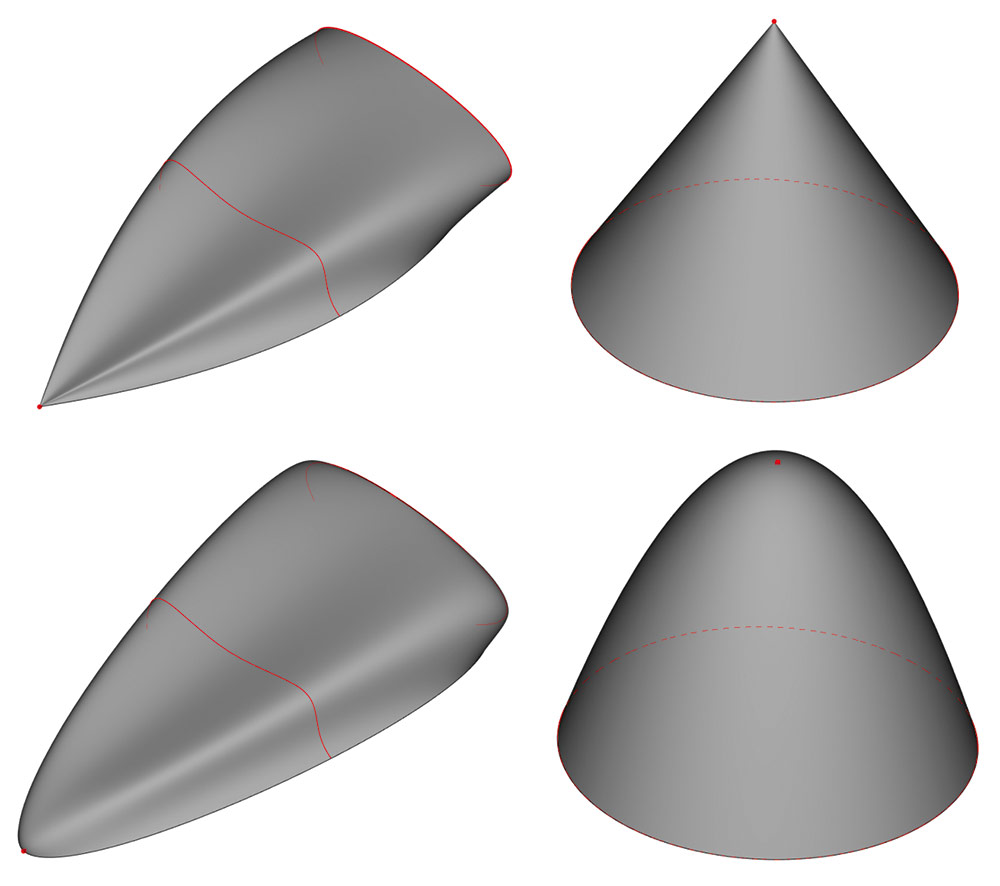
Рис. 13. Примеры операции «По сечениям» с касанием в вершине (верхние поверхности построены без задания условия касания, нижние — с условием)
Значительно улучшены алгоритмы обеспечения построения поверхностей в операции «По сечениям» с соблюдением граничных условий как для продольных (рис. 14), так и поперечных сечений (рис. 15).
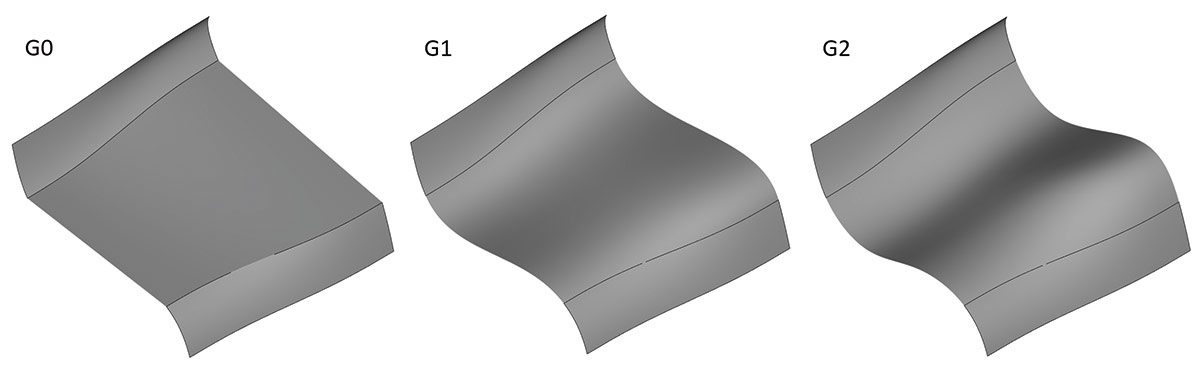
Рис. 14. Примеры операции «По сечениям» с условиями гладкости на продольные сечения
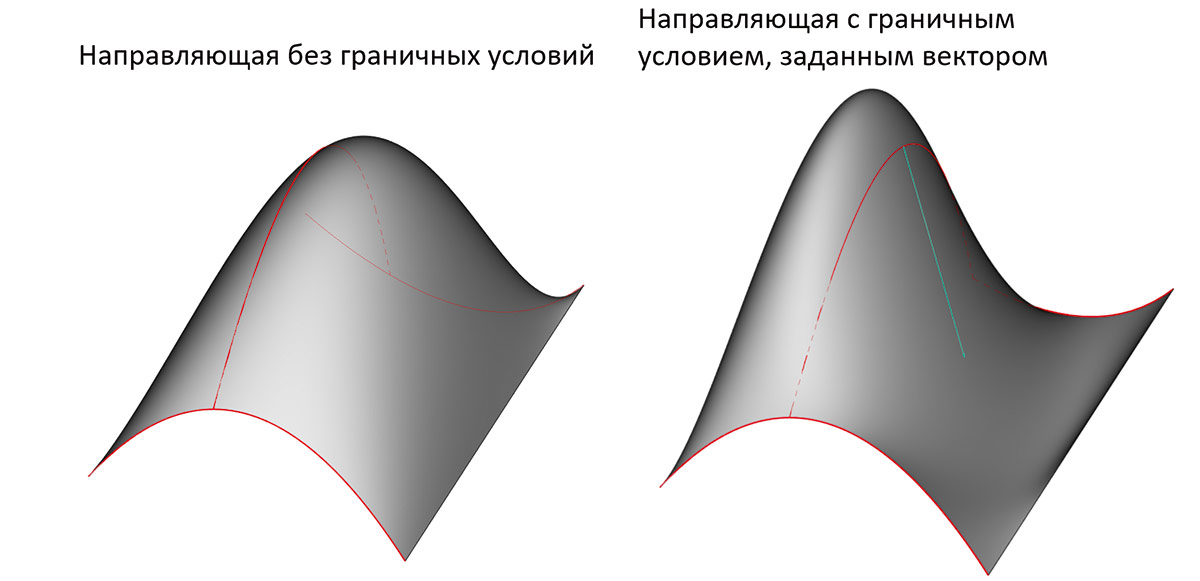
Рис. 15. Примеры операции «По сечениям» с векторным условием касания на поперечном сечении
Кроме того, добавлена возможность указать генератору, на каких сечениях нужно сохранять гладкость, а на каких не требуется (рис. 16).
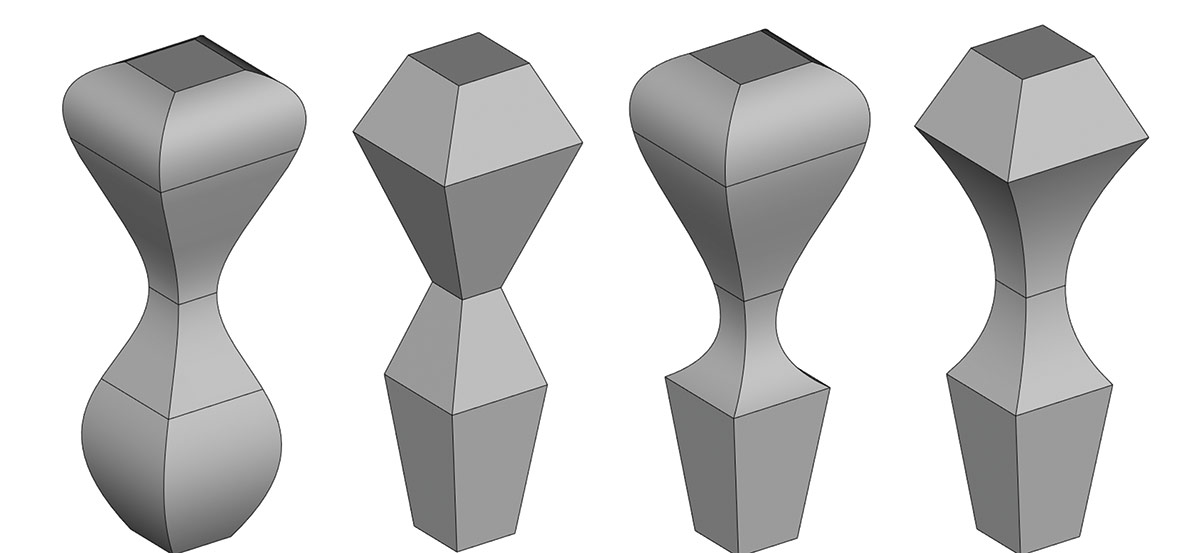
Рис. 16. Примеры работы генератора на одном и том же наборе сечений с указанием разных требований по гладкости в каждом из сечений
Дальнейшее развитие получила функциональность булевых операций. Точнее — инструментов моделирования на основе теоретико-множественной логики, частным случаем которых являются традиционные операции сложения, вычитания и пересечения объемов. Была значительно расширена возможность работы с так называемыми топологиями non-manifold — обобщением понятия твердого тела на комбинацию топологий различной размерности (рис. 17-19).
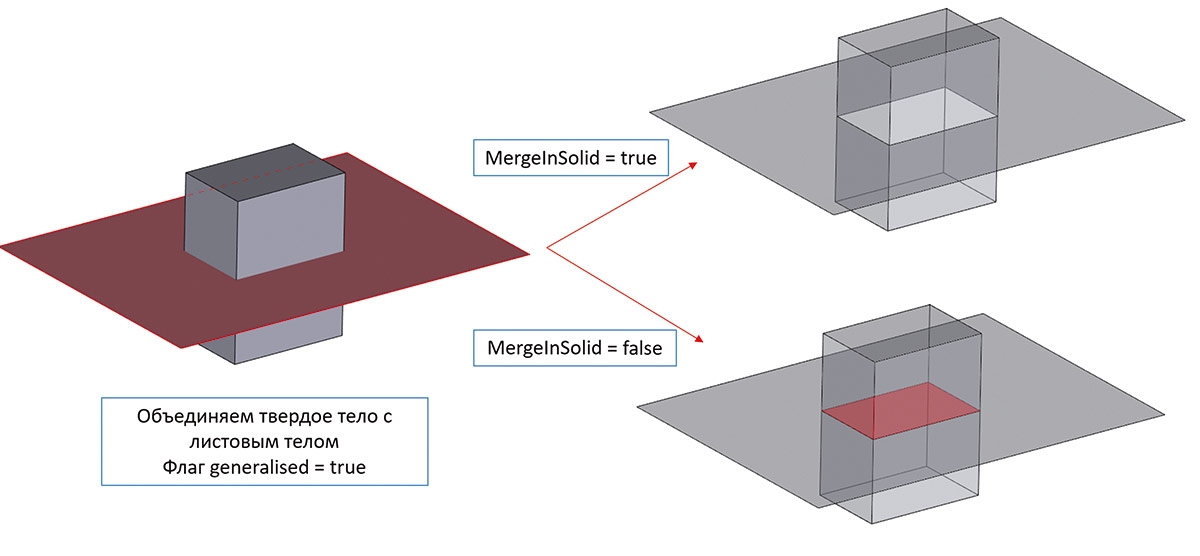
Рис. 17. Пример работы булевого объединения твердого и поверхностного тела с различными значениями опций слияния топологий
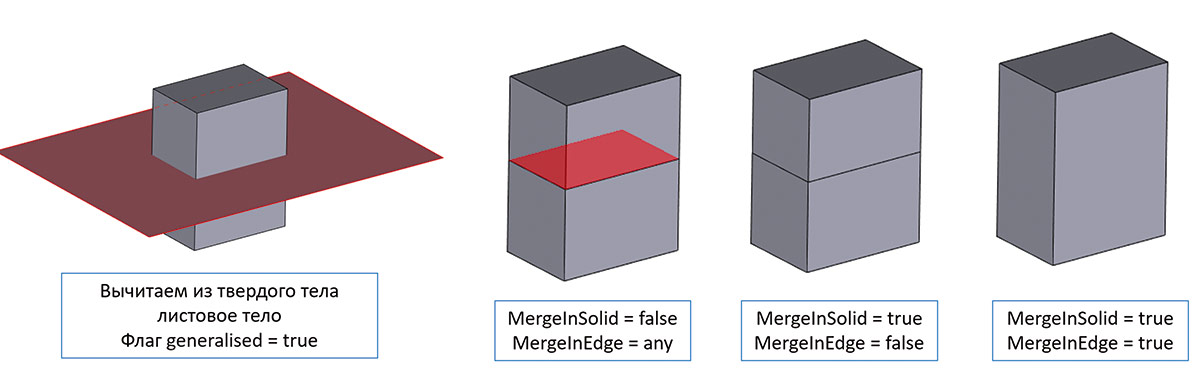
Рис. 18. Иллюстрация различных результатов булевого вычитания в non-manifold случае с различными значениями флагов управления топологией ответов
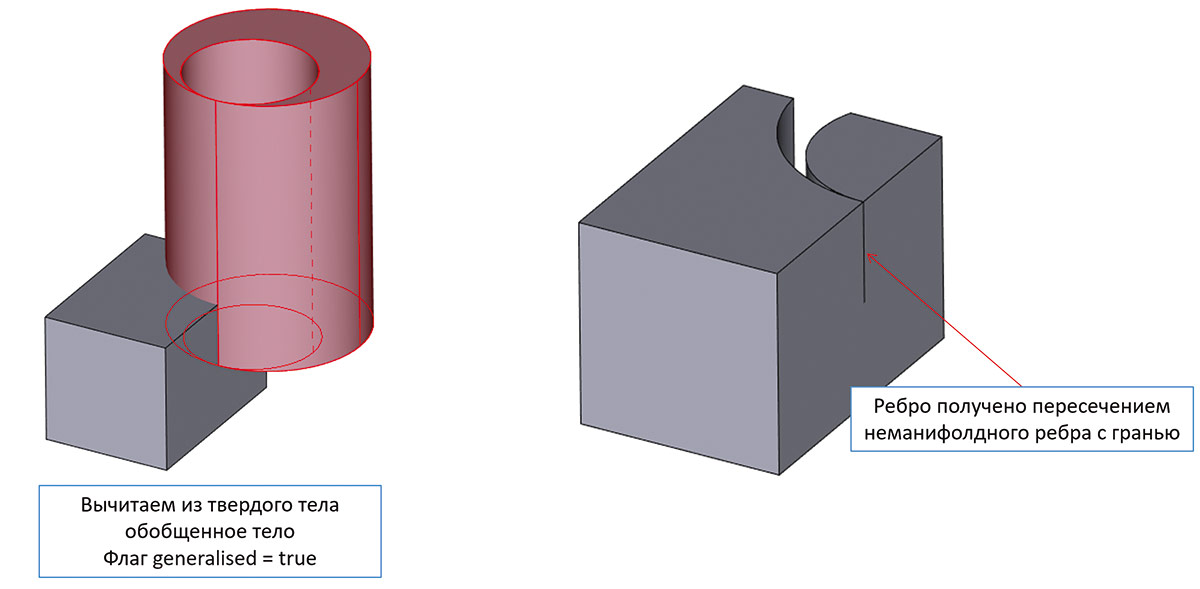
Рис. 19. Пример булевого вычитания тел non-manifold
В текущей версии логика работы с обобщенной топологией доведена до полноты — поддерживаются все требуемые на практике конфигурации, а алгоритмы ядра учитывают в своей работе возникающие топологические обобщения.
Развитие получила также функциональность селективной булевой операции. Раньше эта функциональность не позволяла произвольным образом задавать включаемые и исключаемые регионы и их произвольные комбинации. В текущей версии ядра эти ограничения были сняты. Теперь инструмент позволяет изменять поведение алгоритма в весьма широких пределах. Вот несколько примеров таких возможностей (рис. 20 и 21).
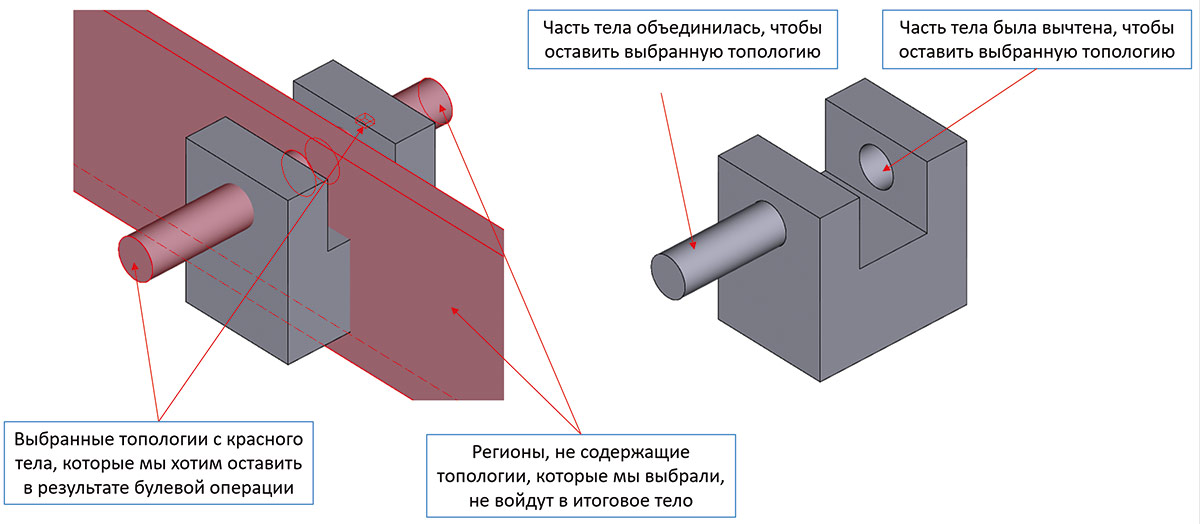
Рис. 20. Иллюстрация возможности комбинации в одной операции разных типов булевых операций над разными частями модели
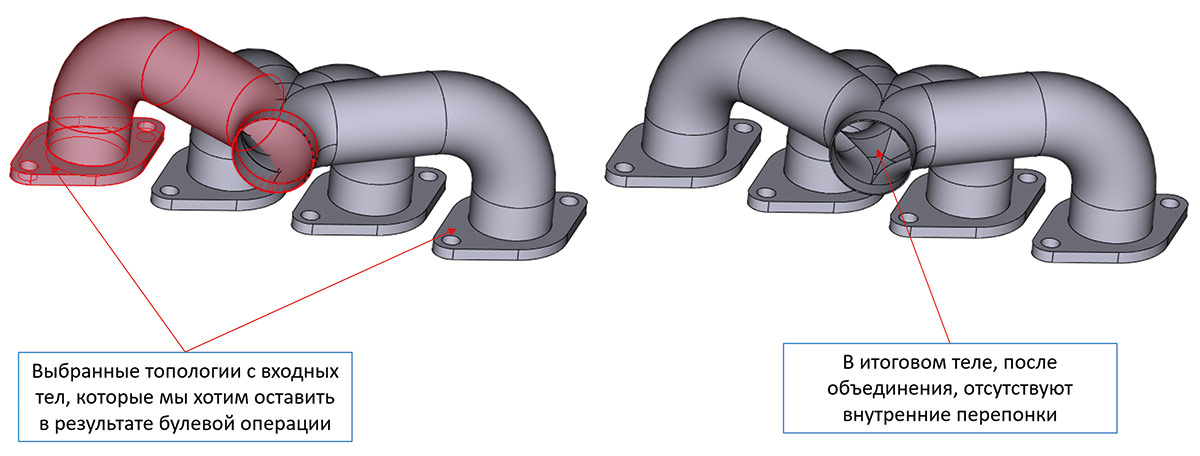
Рис. 21. Пример булевого объединения нескольких тел с отбрасыванием лишней топологии
Развивается в RGK и функциональность локального редактирования модели. В распознавании сглаживаний добавлена поддержка фасок (рис. 22).
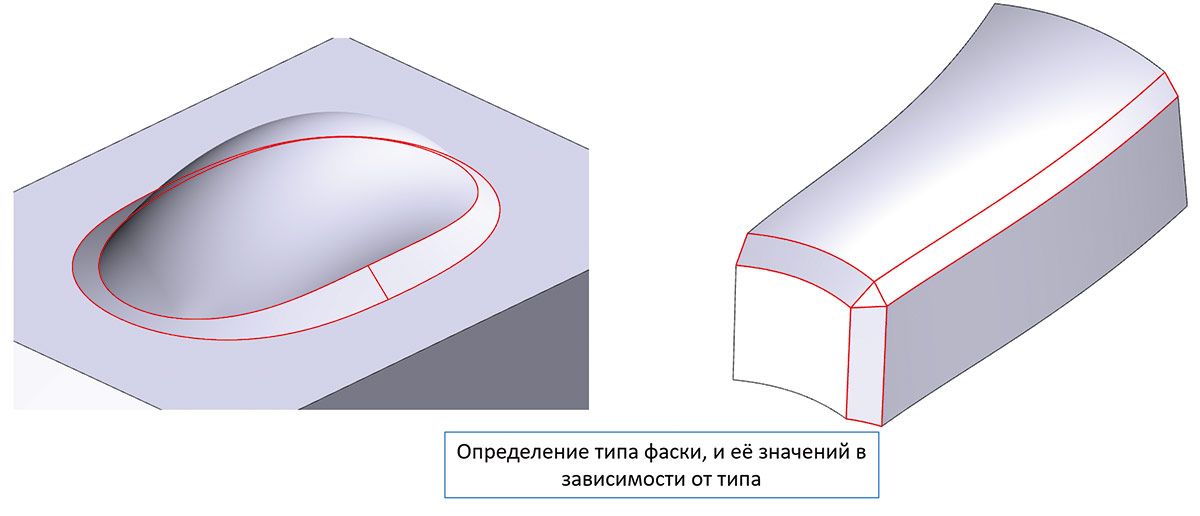
Рис. 22. Автоматическое распознавание фасок на модели
Значительно улучшились возможности ядра в части редактирования сглаживаний с ветвлениями. На рис. 23 и 24 приведены примеры для иллюстрации текущих возможностей.
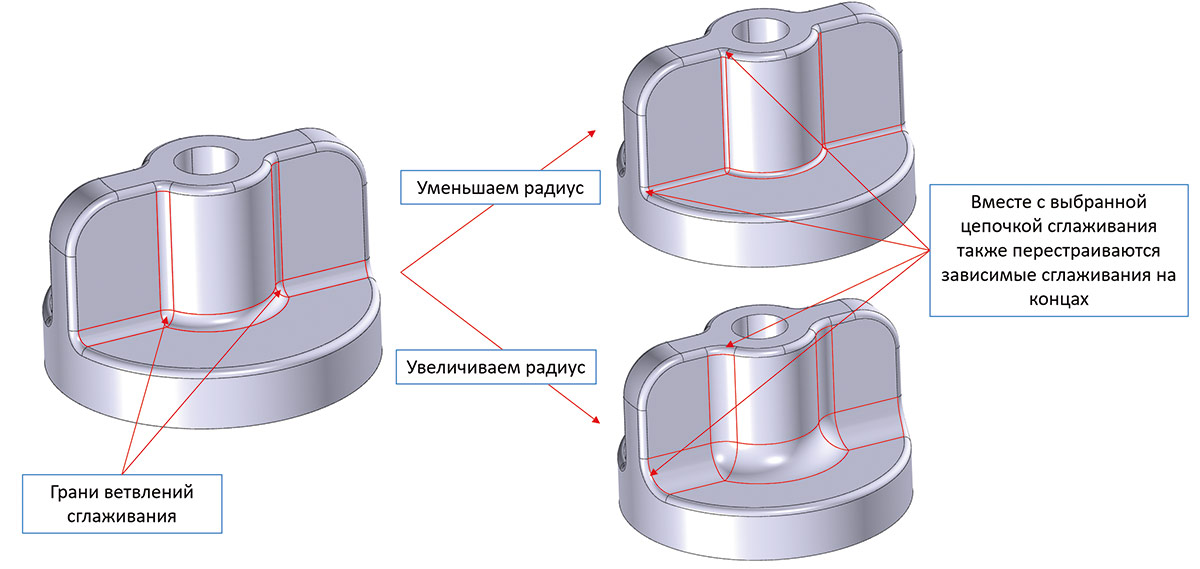
Рис. 23. Пример изменения радиуса сглаживаний с ветвлением и зависимыми гранями
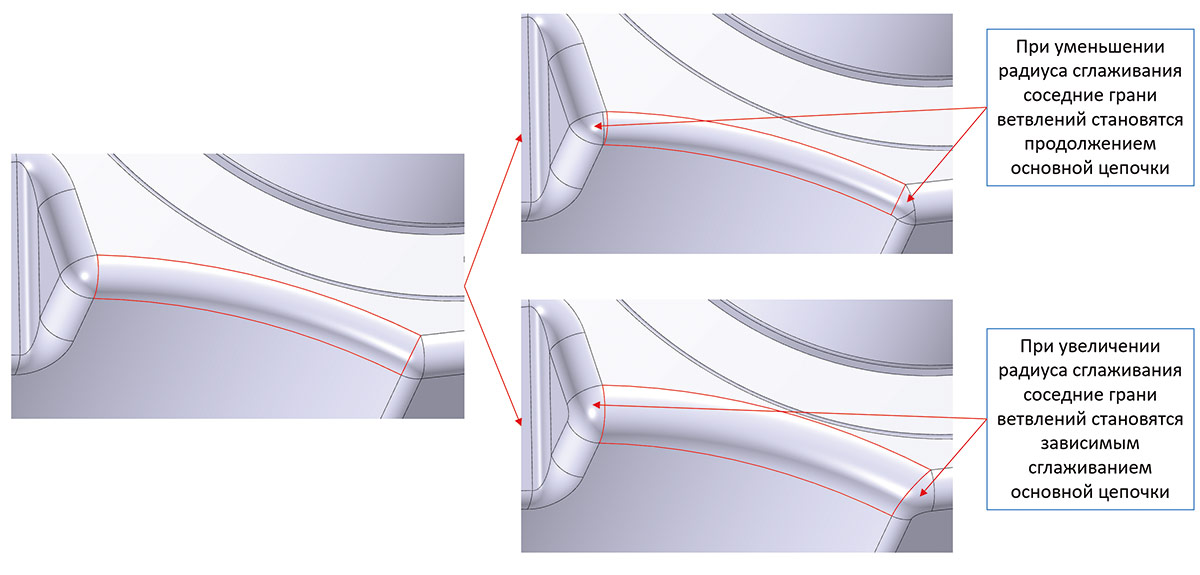
Рис. 24. Изменение радиуса сложной разветвленной цепочки сглаживаний с изменением топологии сглаживания
В рамках работ по улучшению перестроения сглаживаний добавлена также поддержка сглаживаний с переполнениями, что значительно улучшает работу инструмента в практически важных конфигурациях (рис. 25 и 26).
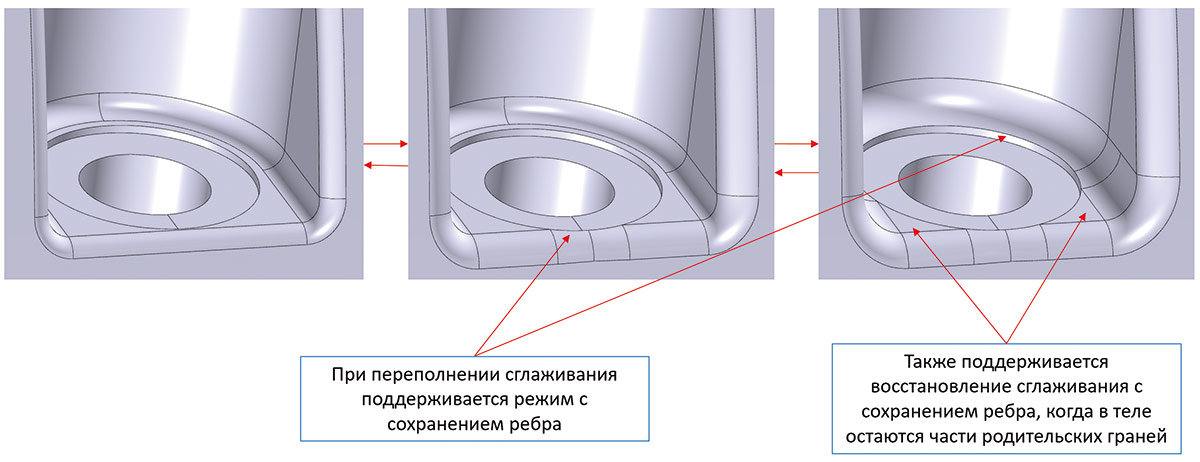
Рис. 25. Пример перестроения сглаживания с учетом возможных переполнений при изменении радиуса
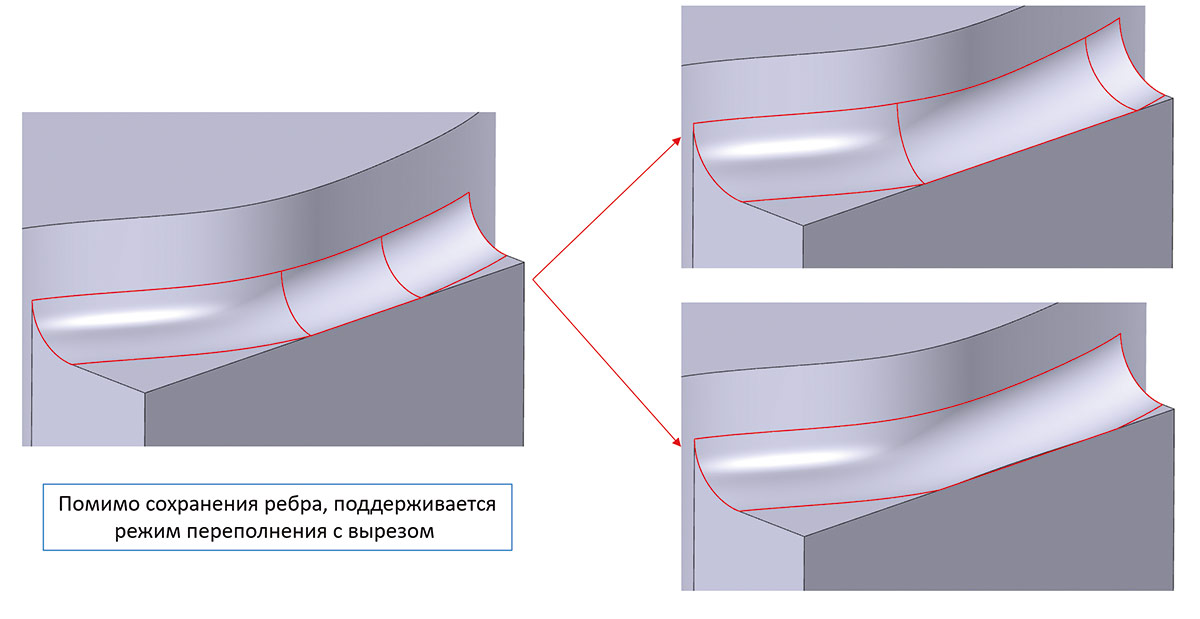
Рис. 26. Пример перестроения сглаживания, показывающий, что обработку переполнений можно менять, подобно тому, как это делается в основном сглаживании
Не стоит на месте и функциональность удаления граней. Были разработаны специализированные инструменты удаления граней сглаживания. Как известно, алгоритмы ядра умеют распознавать сглаживания как постоянного, так и переменного радиусов, но в новой версии появилась специальная обработка удаления сглаживаний, учитывающая информацию из распознавания (рис. 27-29).
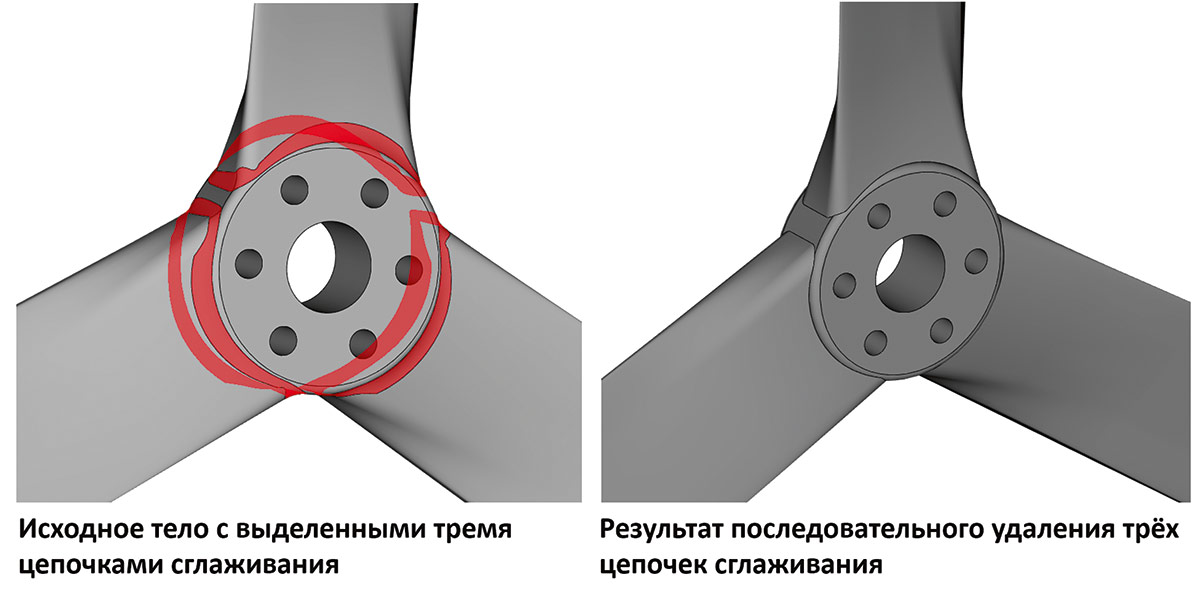
Рис. 27. Пример работы удаления граней сглаживания из нескольких цепочек
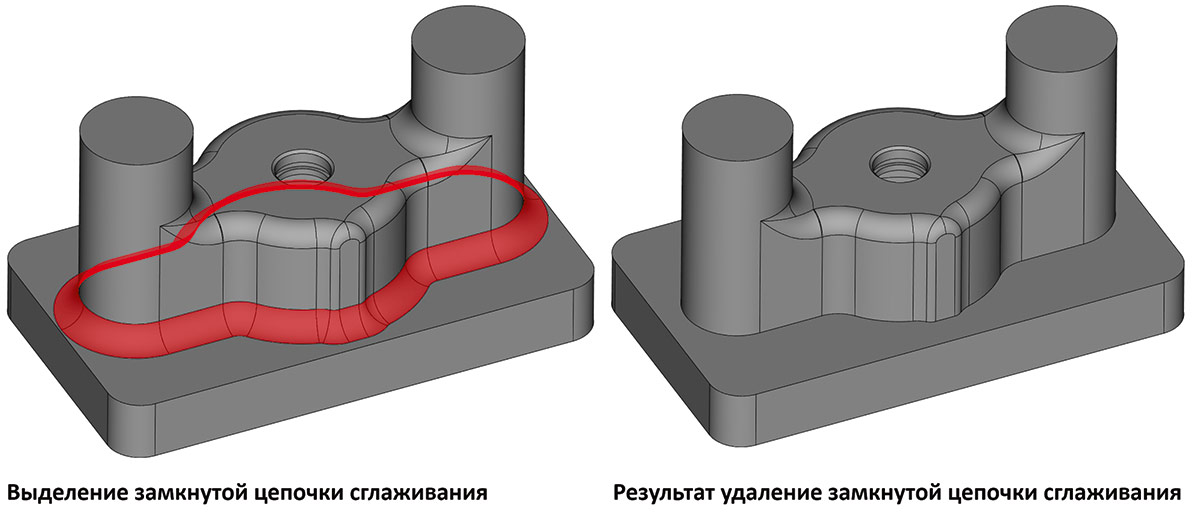
Рис. 28. Пример удаления замкнутой цепочки сглаживаний
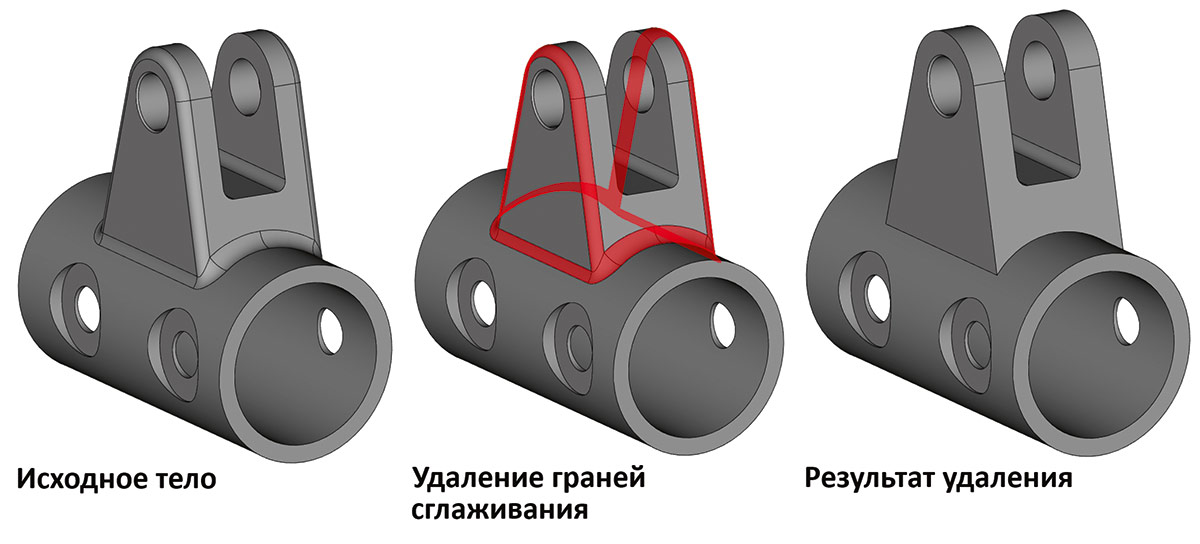
Рис. 29. Пример удаления цепочек сглаживания с ветвлениями
Особое развитие получил и общий алгоритм удаления граней. Теперь он умеет обрабатывать более сложные конфигурации (рис. 30 и 31).
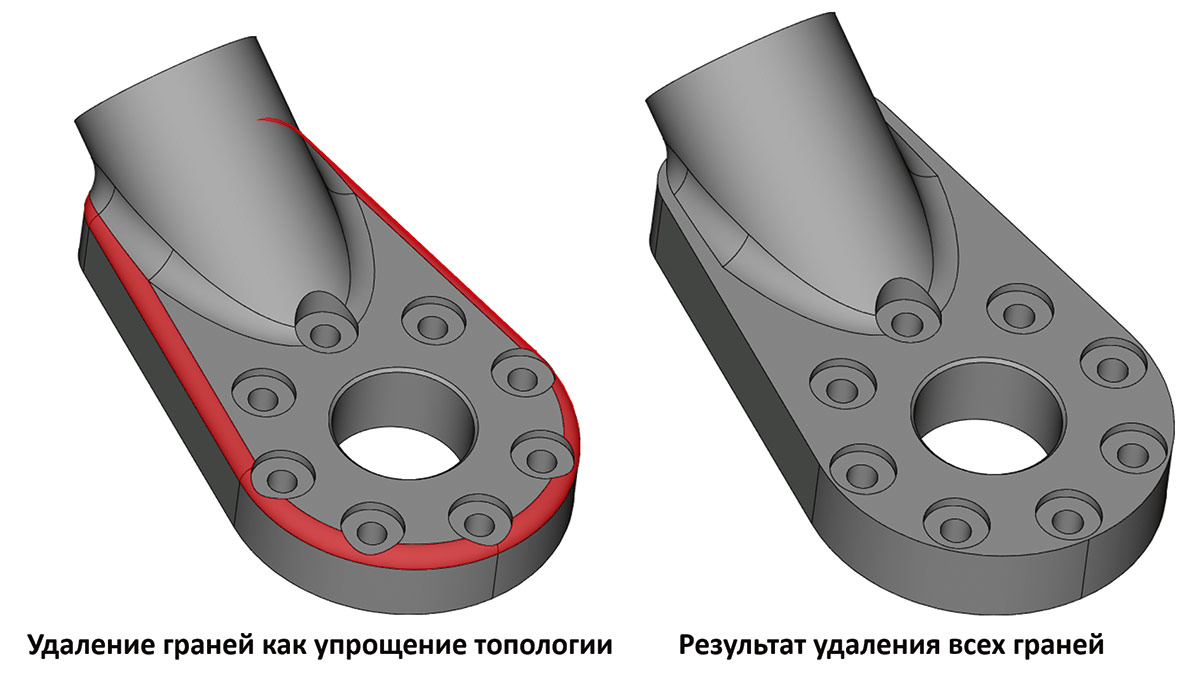
Рис. 30. Пример удаления граней с восстановлением исходной топологии
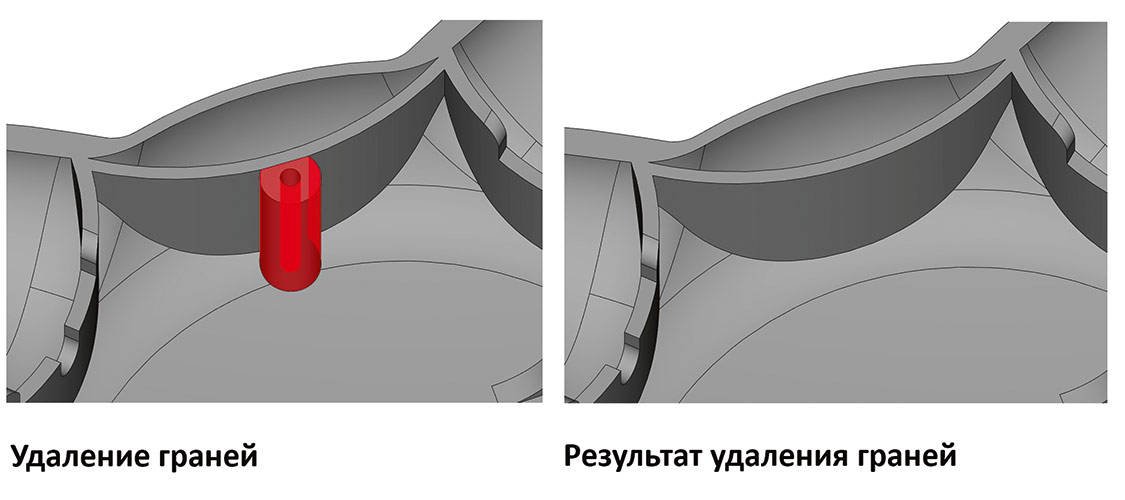
Рис. 31. Пример работы общего алгоритма удаления граней
Улучшения получила функциональность построения уклонов граней. Была добавлена возможность вычисления кривых — изоклин по направлению уклона и углу уклонения, и использование этих кривых в качестве неподвижных ребер уклона (рис. 32).
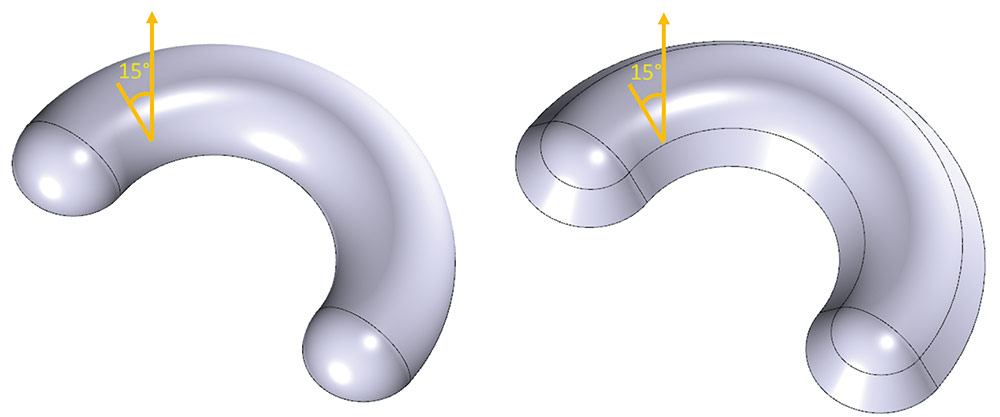
Рис. 32. Построение уклона граней с предварительным разрезанием изоклиной
В новой версии возможно задание поверхности разъема (поверхностного тела), лежащей за пределами уклоняемых граней, и даже твердого тела (рис. 33 и 34).
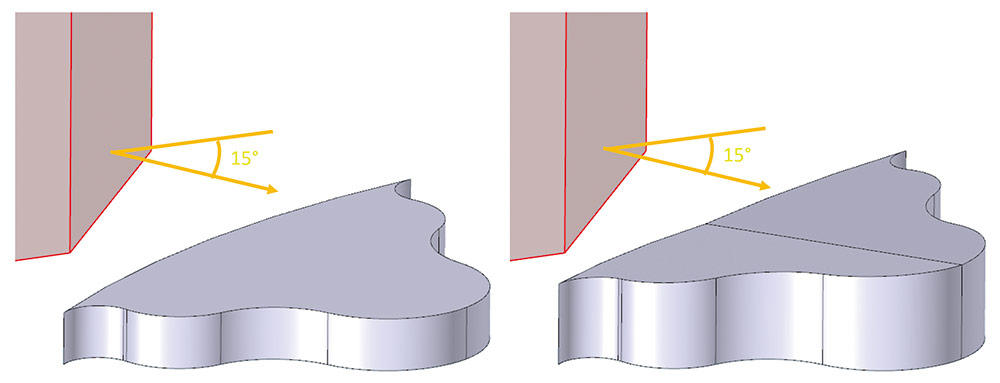
Рис. 33. Построение уклона с указанием поверхностного тела как неподвижной геометрии, так что уклоняемые грани формируются относительно неподвижной геометрии
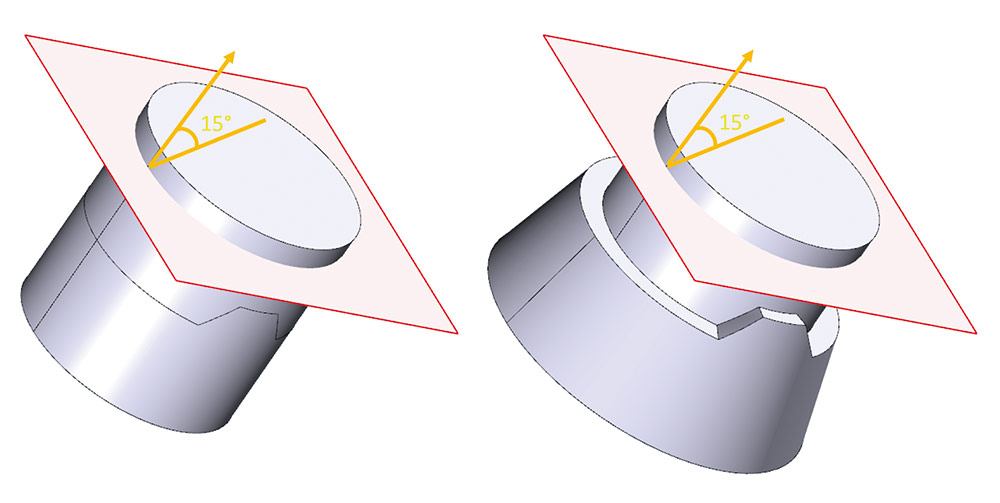
Рис. 34. Пример уклонения грани, в котором неподвижная геометрия не пересекает грань
Появилась возможность задания ребер и граней для построения ступенек в уклоне (рис. 35).
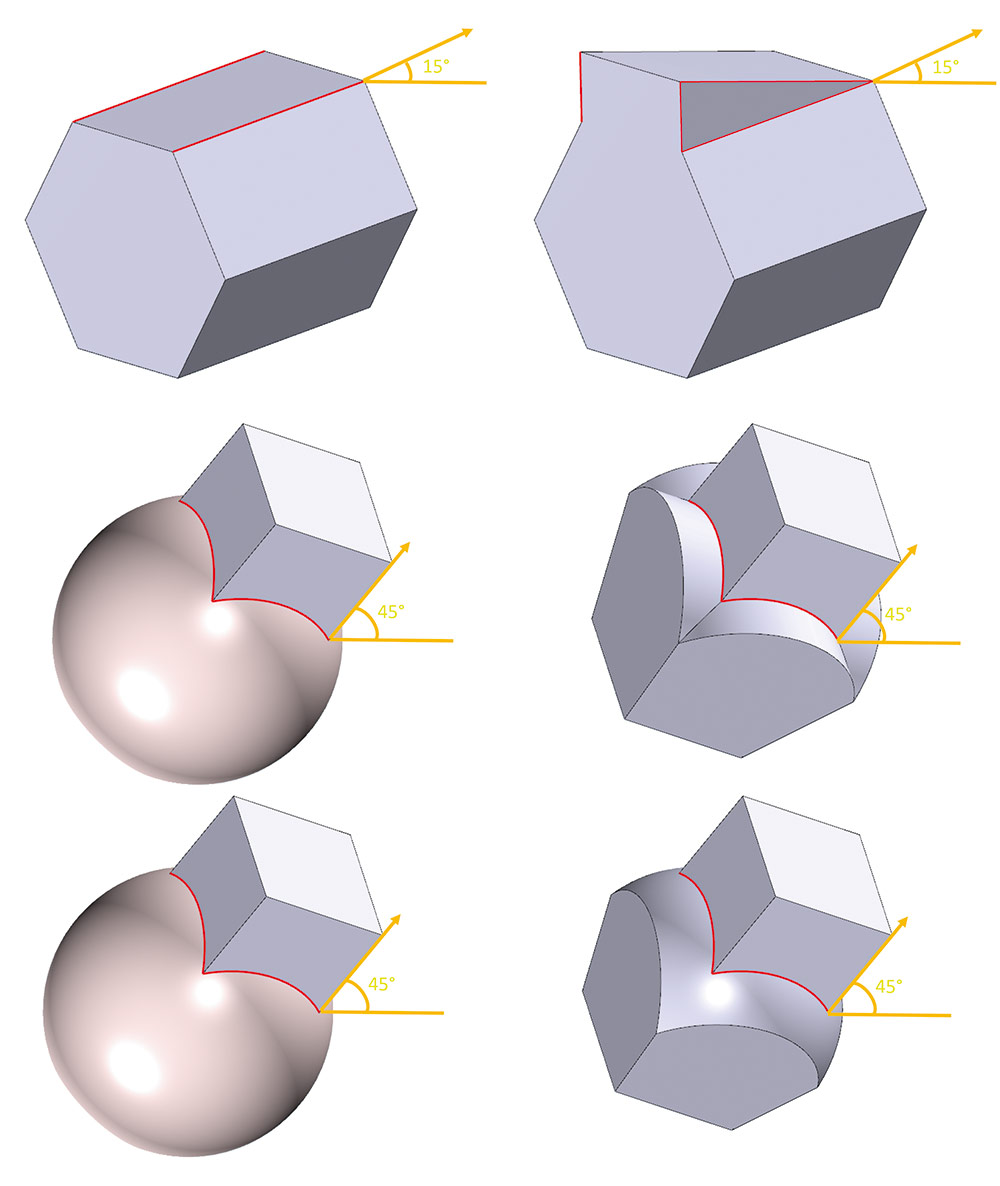
Рис. 35. Доступные опции в построении уклона граней с построением ступенек (с указанием ребер отрыва и поверхности разъема со ступенькой как по нормали, так и по поверхности)
В генераторе построения оболочек появилась поддержка изменения топологии тела при смещении. Тем самым поддерживается возможность вырождения топологических элементов (рис. 36).

Рис. 36. Пример вырождения граней при построении оболочки внутрь тела (при заданном смещении пропадают грани сглаживания)
Традиционно, значительное развитие получила функциональность RGK в части построения сглаживаний ребер и граней. Как известно по предыдущим обзорам функциональности ядра, развитие происходит в двух основных направлениях: расширение списка решаемых геометрических задач и совершенствование топологических алгоритмов. В обоих этих направлениях в новой версии разработчиками достигнуты значительные успехи. В первую очередь рассмотрим геометрическую часть задачи. Для начала остановимся на обработке ситуации, когда при построении поверхности может получиться самопересечение поверхностей сглаживания. Как известно, ранее в RGK уже были разработаны алгоритмы, которые позволяют бороться с некоторыми типами таких сложностей. В новой версии эти инструменты получили дальнейшее развитие. Во-первых, были улучшены методы поиска границ области самопересечения. Во-вторых, разработана математика коррекции границы такой области — регуляризации задачи — и применена новая математика генерации поверхностей сглаживания для областей сложной формы (рис. 37). Это позволило решать весьма сложные постановки, ранее доступные только паре-тройке геометрических ядер в мире.
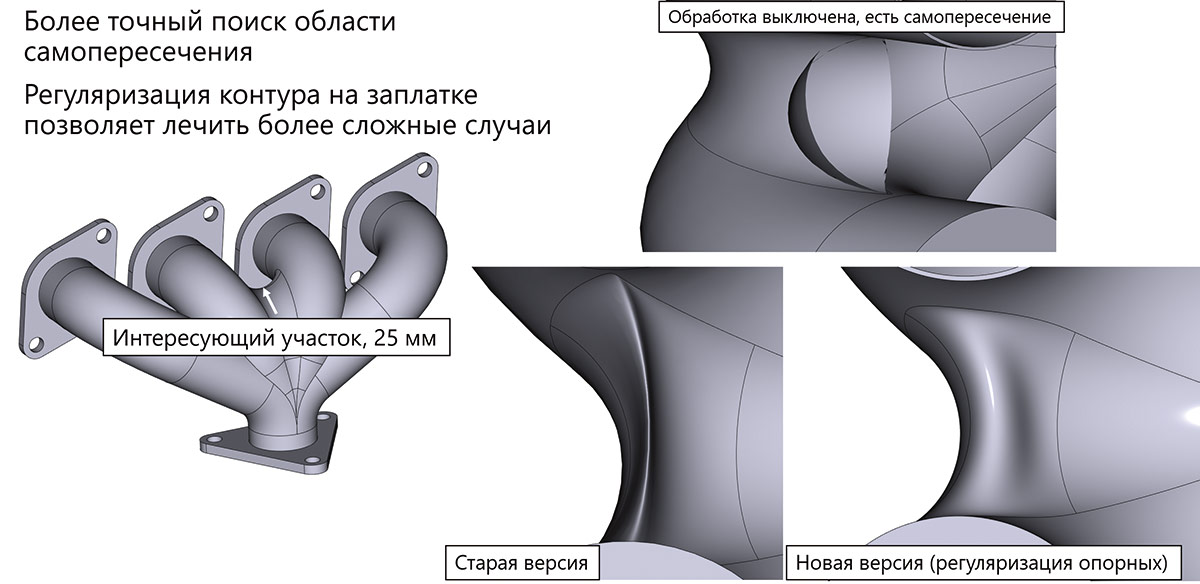
Рис. 37. Пример построения сглаживания в зоне самопересечения с применением силы большого радиуса
Добавились новые типы поверхностей сглаживания. В частности, теперь поддерживается переменная ширина поверхности сглаживания (рис. 38-41).
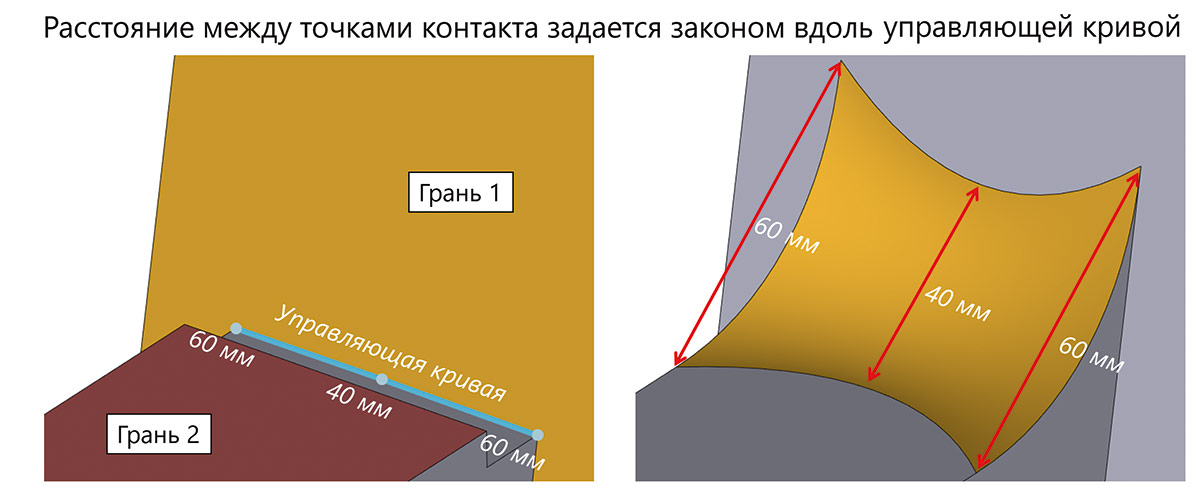
Рис. 38. Иллюстрация схемы построения поверхности сглаживания переменной ширины
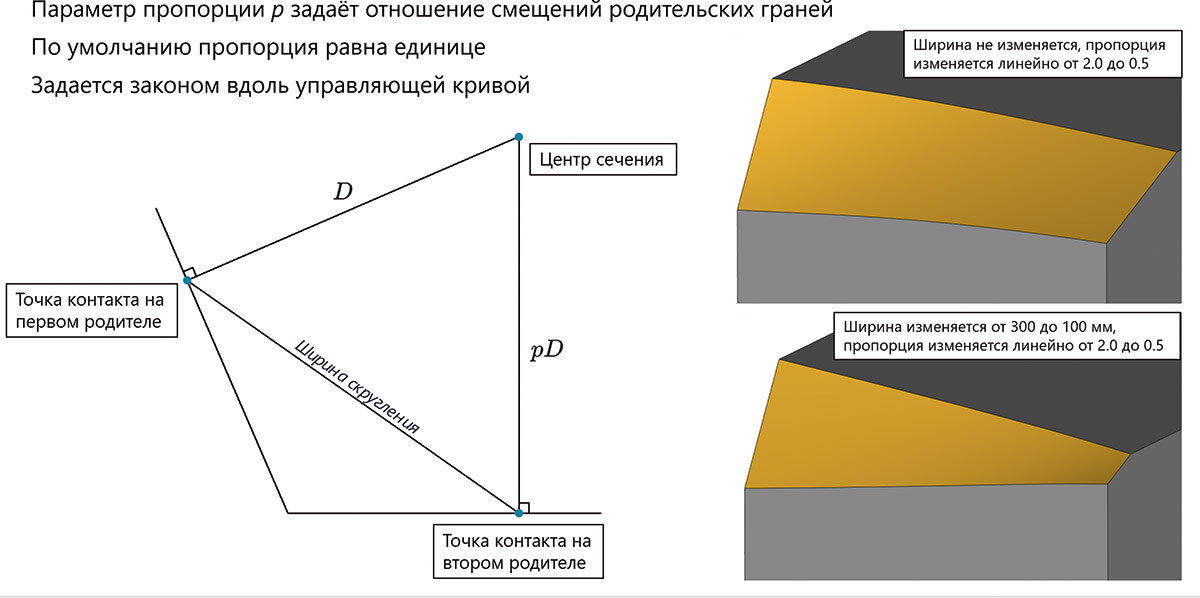
Рис. 39. Управляющие параметры режима переменной ширины сглаживания
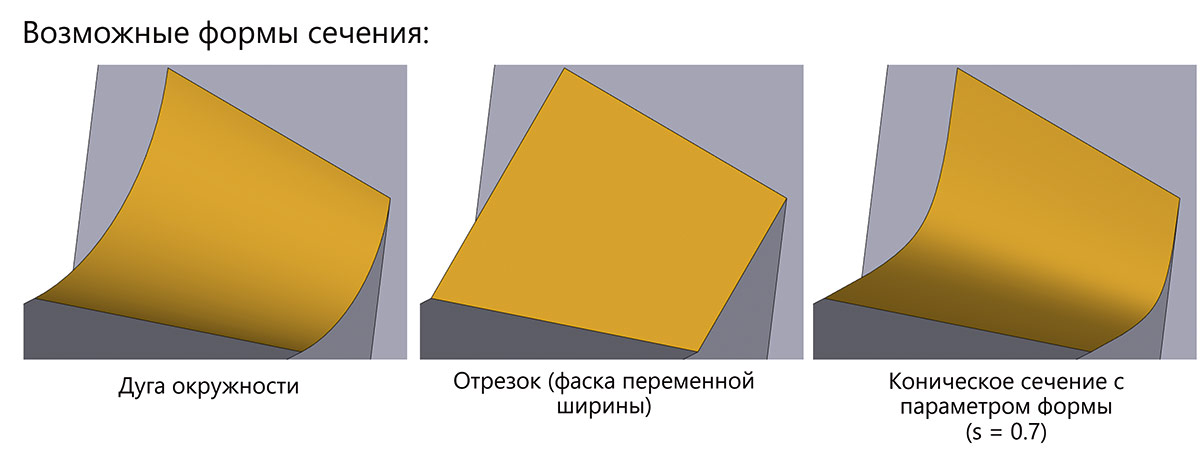
Рис. 40. Примеры возможных форм сечений в режиме переменной ширины
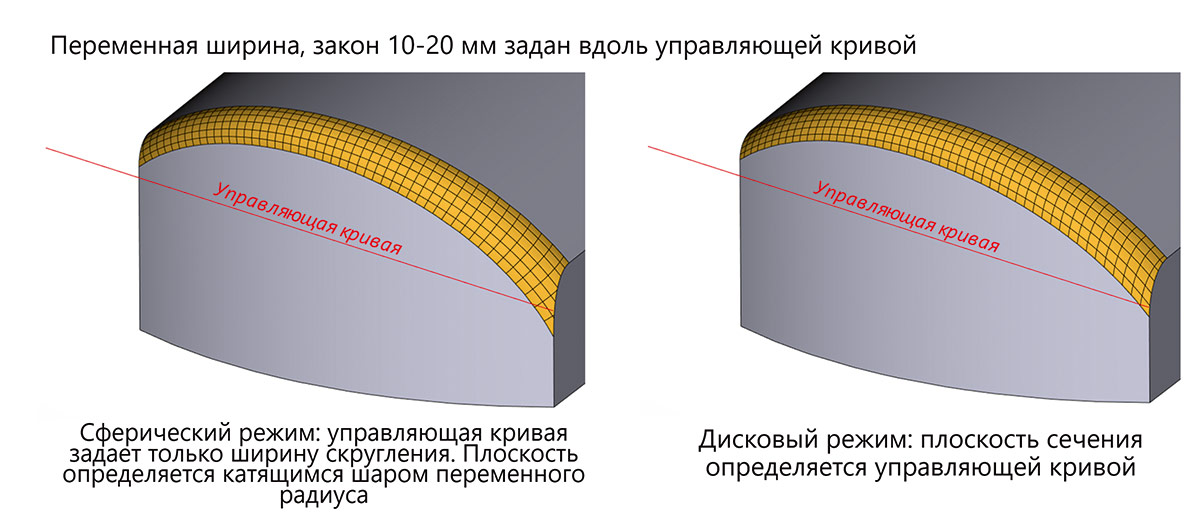
Рис. 41. Пример работы нового режима в случае «катящегося шарика» и дискового сглаживания
Завершена работа над так называемым коническим сглаживанием, когда величины смещений могут определяться кривыми на сопрягаемых поверхностях. На рис. 42 показано, как это выглядит.
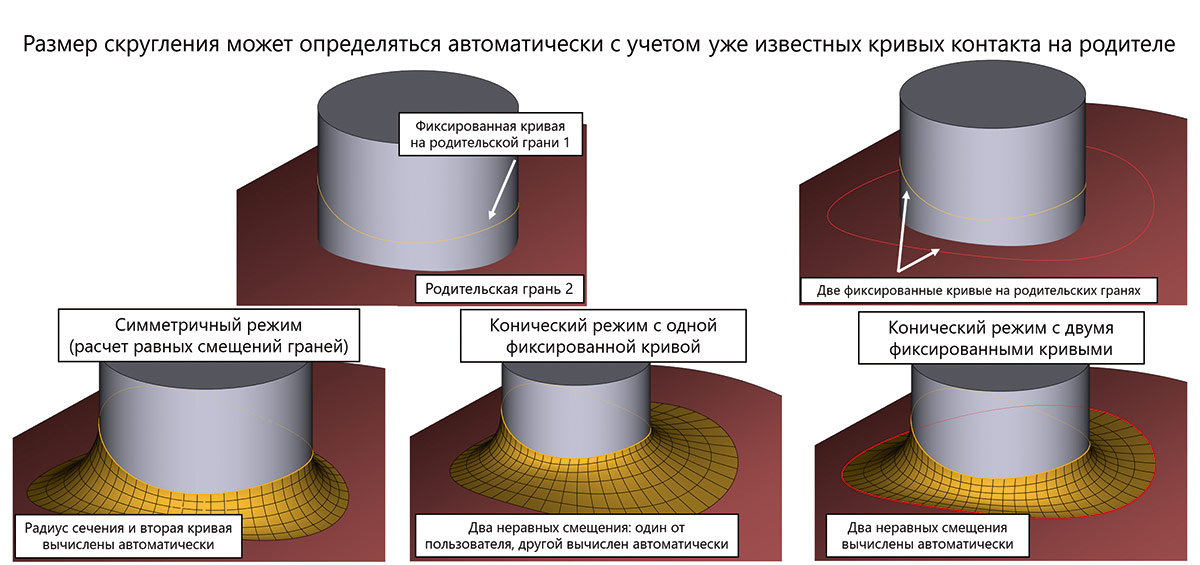
Рис. 42. Иллюстрация режимов «конических» сглаживаний
Следует напомнить, что архитектура алгоритмов сглаживания RGK позволяет использовать комбинацию различных параметров операции: формы сечения, ориентации сечения, величин и характеристик смещений и т.д. Более наглядно эти возможности представлены в таблице на рис. 43.
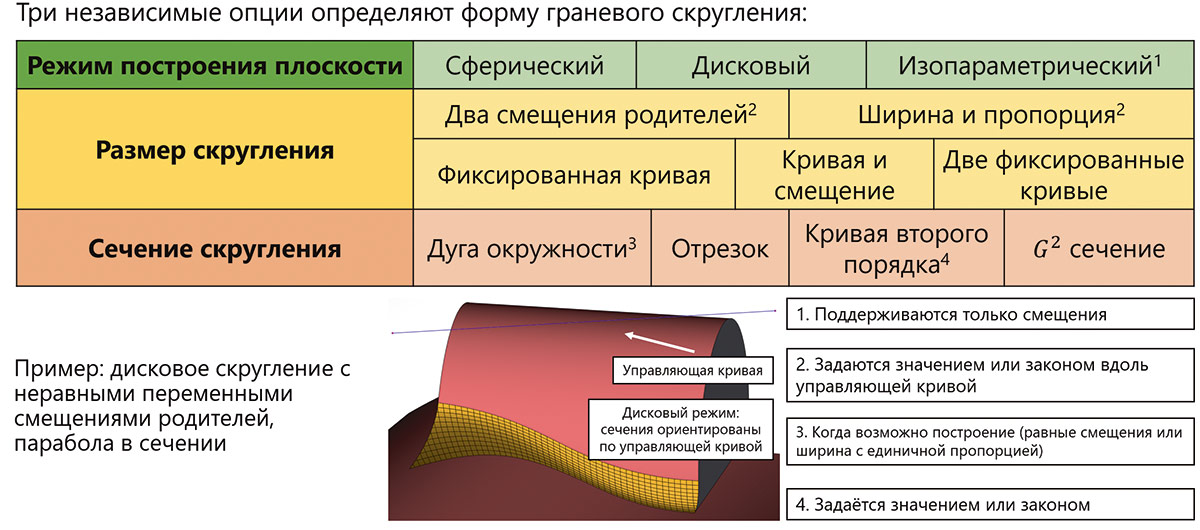
Рис. 43. Таблица, иллюстрирующая режимы сглаживания RGK
В настоящее время можно утверждать, что все практически значимые комбинации параметров ядро RGK поддерживает. В этом отношении достигнут паритет с ведущими мировыми геометрическими ядрами. Помимо общих постановок задач в математике часто есть большое число важных, но не очень наглядных вопросов, которые, тем не менее, требуют решения для получения практически полезного результата. Осознавая это, разработчики ядра RGK тратят значительные усилия на усовершенствование алгоритмов для обеспечения необходимого качества результата. Работа в этом направлении ведется постоянно. Подробнее об этом будет рассказано в следующем номере журнала «САПР и графика».



