* Окончание, начало см. «САПР и графика», № 6’2025.
Компания «Топ Системы» делится результатами работы команды разработчиков за прошедший период. Работа была проведена масштабная и разноплановая: изменения затронули как функциональность API ядра, так и его базовые внутренние алгоритмы. В первой части статьи («САПР и графика», № 6’2024) уже было рассказано о ключевых направлениях развития. Во второй части подробнее остановимся не только на новой функциональности ядра, но и на важных внутренних улучшениях и алгоритмах, которым была посвящена значительная часть усилий команды.
В настоящее время можно утверждать, что все практически значимые комбинации параметров ядро RGK поддерживает. В этом плане достигнут паритет с ведущими мировыми геометрическими ядрами. Помимо общих постановок задач, в математике, как правило, есть большое число важных, но не очень наглядных вопросов, которые, тем не менее, требуют решения для получения практически полезного результата. Осознавая это, разработчики ядра RGK прилагают серьезные усилия на усовершенствование алгоритмов, обеспечивающих получение необходимого качества результата.
Такого плана работа ведется постоянно, хотя результаты при беглом просмотре не всегда заметны. Тем не менее мы считаем, что качество геометрии крайне важно и в значительной мере отличает промышленные ядра от других. Проиллюстрируем эту мысль на одном примере. Рассмотрим сглаживание переменного радиуса с линейной функцией изменения радиуса. Задача эта уже довольно давно решается в RGK, но качество результата не устраивало разработчиков ядра, так как гладкость поверхности сглаживания на стыках граней не всегда хорошо обеспечивалась именно при честной линейной функции радиуса (рис. 44).
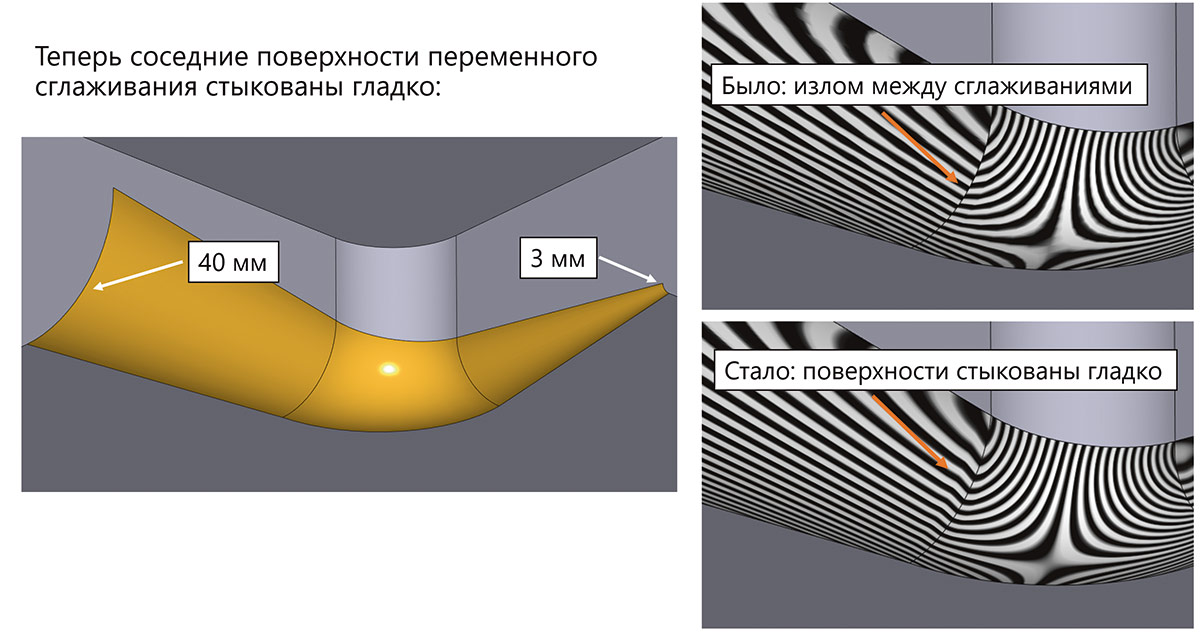
Рис. 44. Иллюстрация проблемы излома касательной плоскости при линейном изменении радиуса и поведения алгоритма сглаживания в новой версии ядра
Не будем останавливаться на математических аспектах задачи, отметим только, что подобные решения зачастую бывают нетривиальными. Прежнее поведение — это не «ошибка алгоритма», как кто-то может подумать, а формально верный ответ в задаче сглаживания. Однако хотелось бы получить поверхность лучшего качества, что и было достигнуто в новой версии. Подобных улучшений качества решения задач в различных алгоритмах ядра немало, хотя это на первый взгляд и не заметно.
В генераторе сглаживания предыдущей версии RGK была заявлена функциональность построения Y-формы обработки вершины. В новой версии эта функциональность также получила свое развитие. Рассмотрим на примерах, что теперь умеет этот инструмент (рис. 45 и 46).
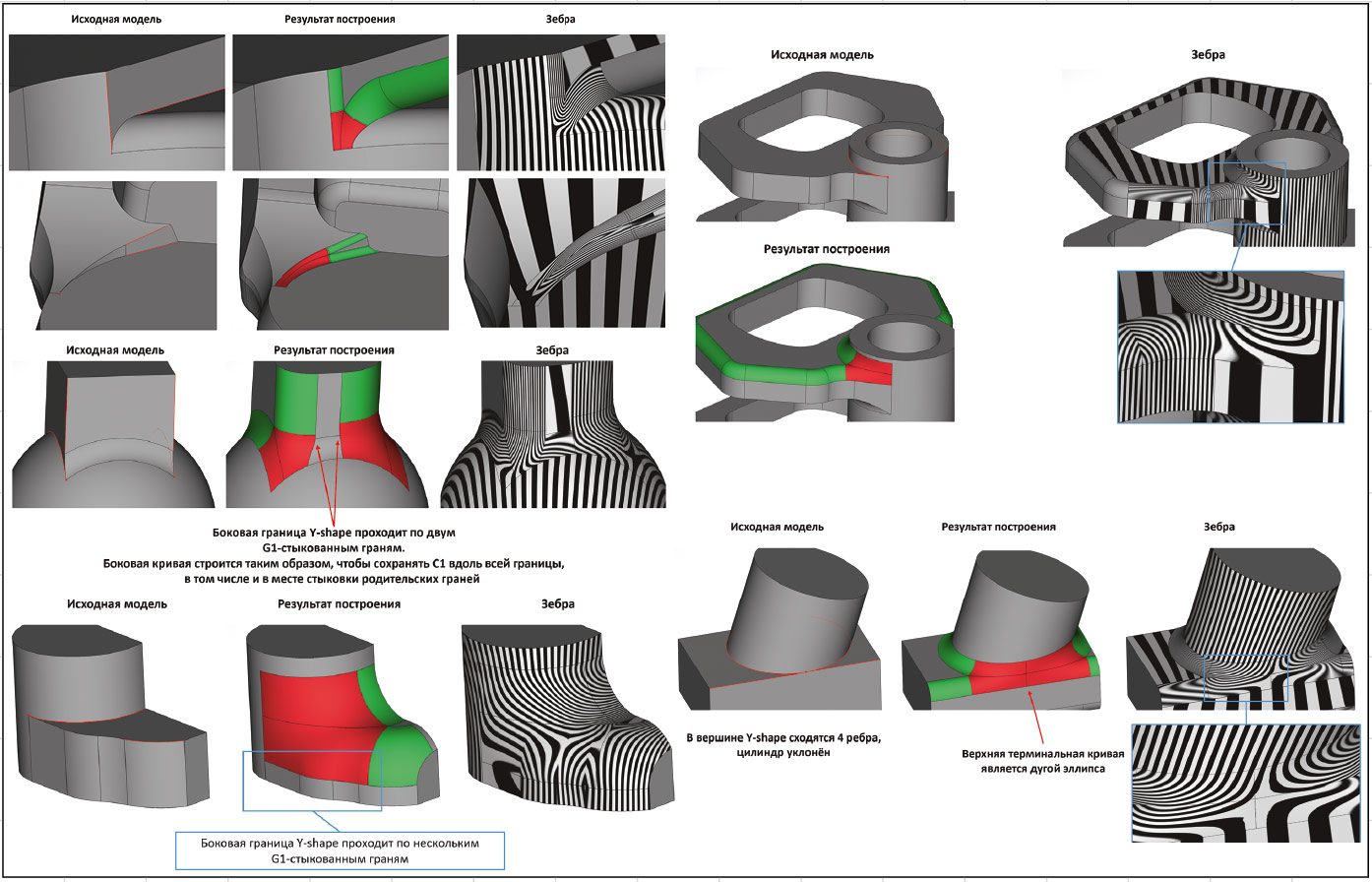
Рис. 45. Примеры работы Y-формы в новой версии ядра
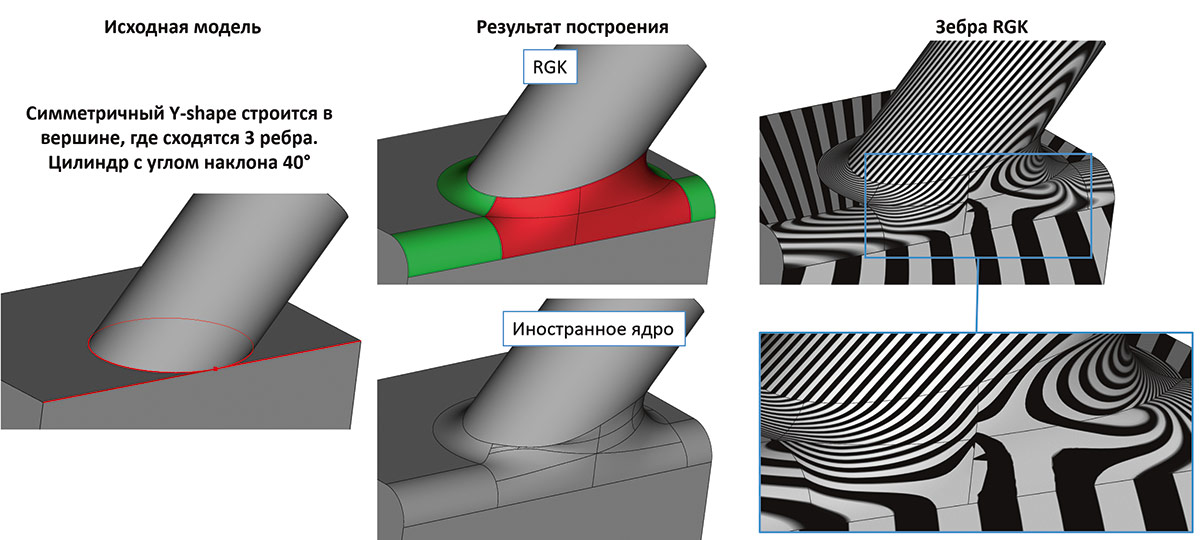
Рис. 46. Иллюстрация сравнения поведения алгоритма Y-формы с известным иностранным конкурирующим ядром
Приведенные выше примеры, в частности, иллюстрируют, насколько кропотливо и ответственно подходит команда RGK к отработке принципиальных вопросов в математике ядра, в силу понимания особой значимости аспектов качества конечных моделей в приложениях.
Как отмечалось, изменения затронули не только геометрические аспекты сглаживания, но и, даже в большей степени, возможности топологического алгоритма. Если возможности Y-формы — это функциональность на стыке геометрии и топологии, то, например, возможности построения составной заплатки — это больше логика управляющего алгоритма топологического свойства (рис. 47).

Рис. 47. Иллюстрация поддержки многосегментной «заплатки» в алгоритмах сглаживания переменного радиуса
Особое внимание было уделено улучшению надежности алгоритмов с учетом точностей исходных моделей (рис. 48 и 49).
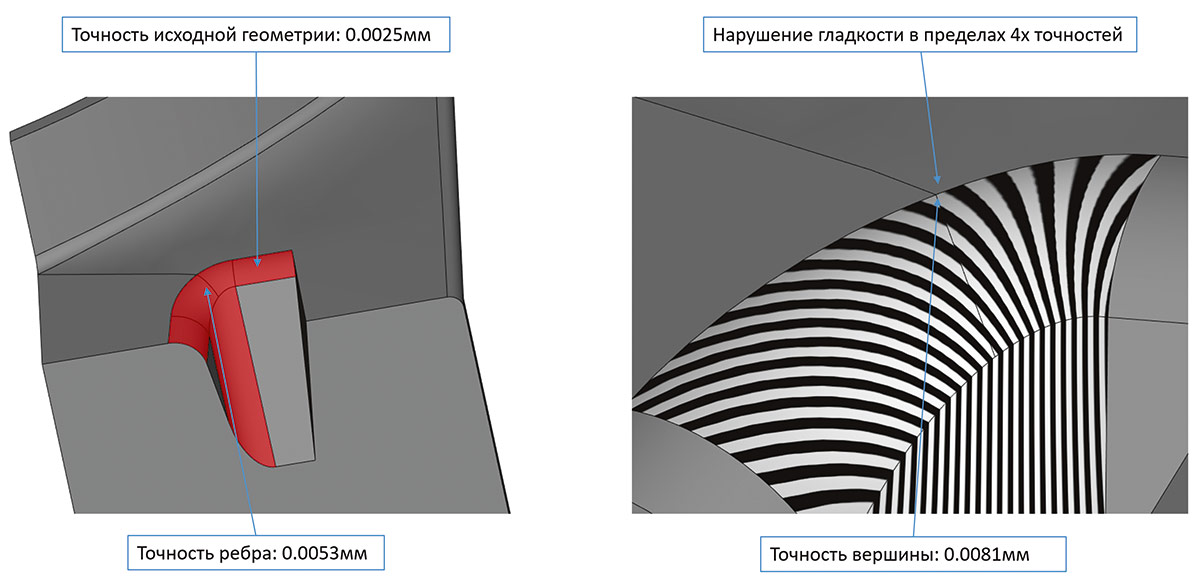
Рис. 48. Пример обработки через «почти касательное» ребро с корректировкой фактической точности топологии
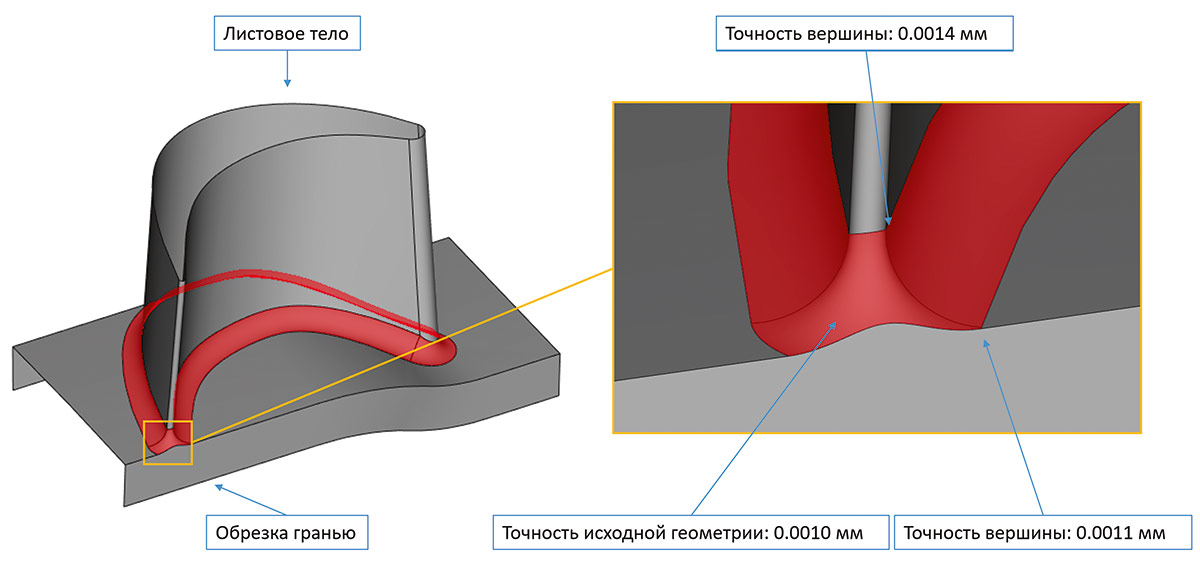
Рис. 49. Иллюстрация учета точности входной геометрии в ситуации обрезки боковой гранью
Кроме того, был снят ряд ограничений в алгоритмах перекрытия сглаживающих последовательностей. На рис. 50 приведено несколько примеров, которые теперь обрабатываются новой обобщенной логикой.
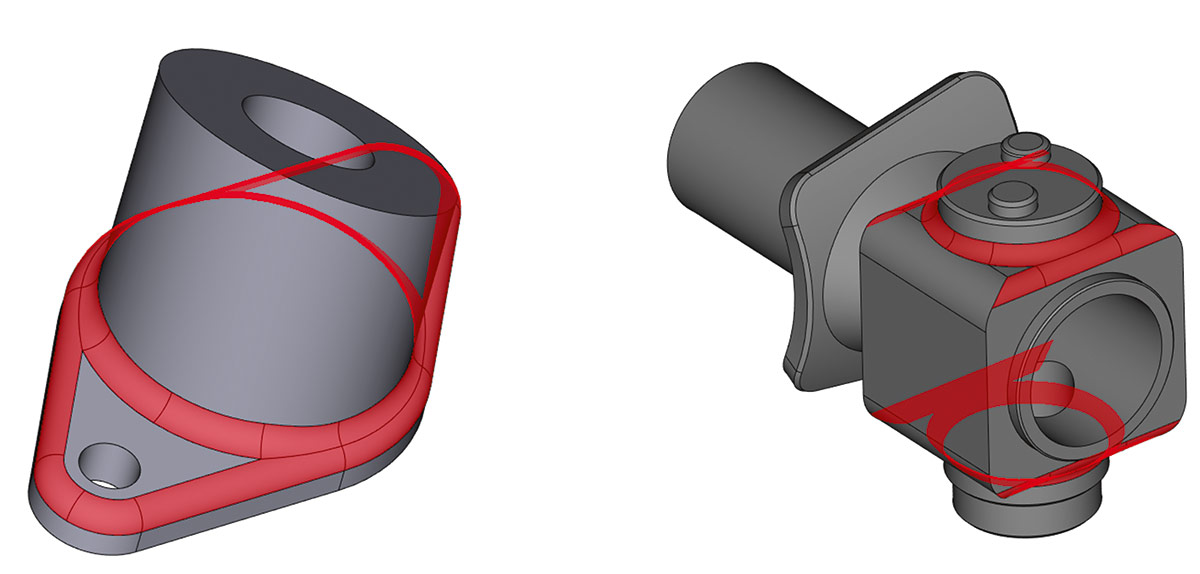
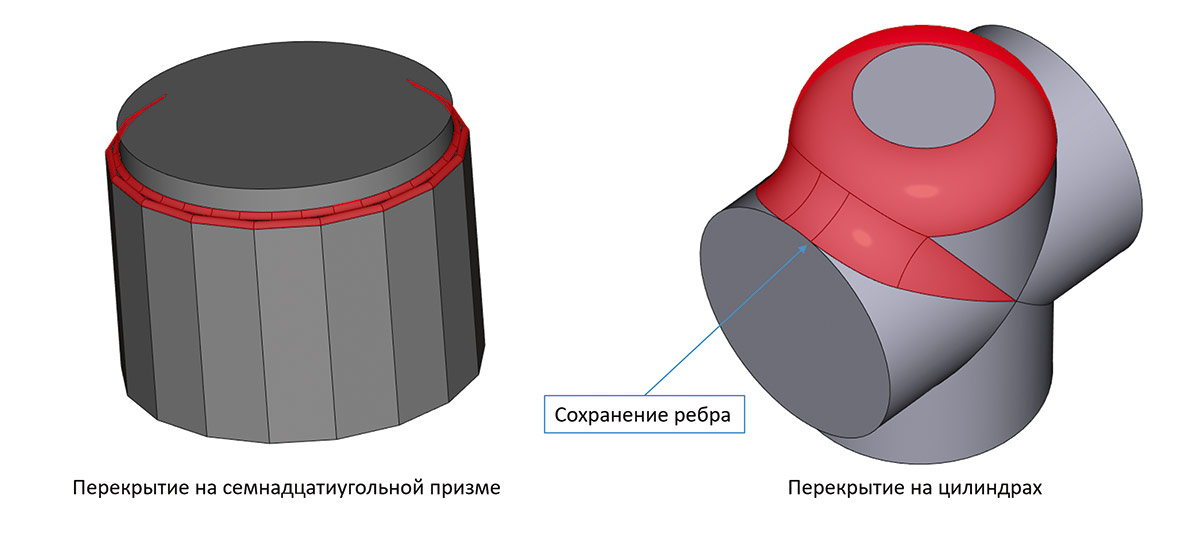
Рис. 50. Примеры перекрытия сглаживающих последовательностей (построение сглаживания за одну операцию)
Ослаблены ограничения в топологии трех- и четырехреберных обработок, сходящихся в одну вершину ребер (рис. 51 и 52).
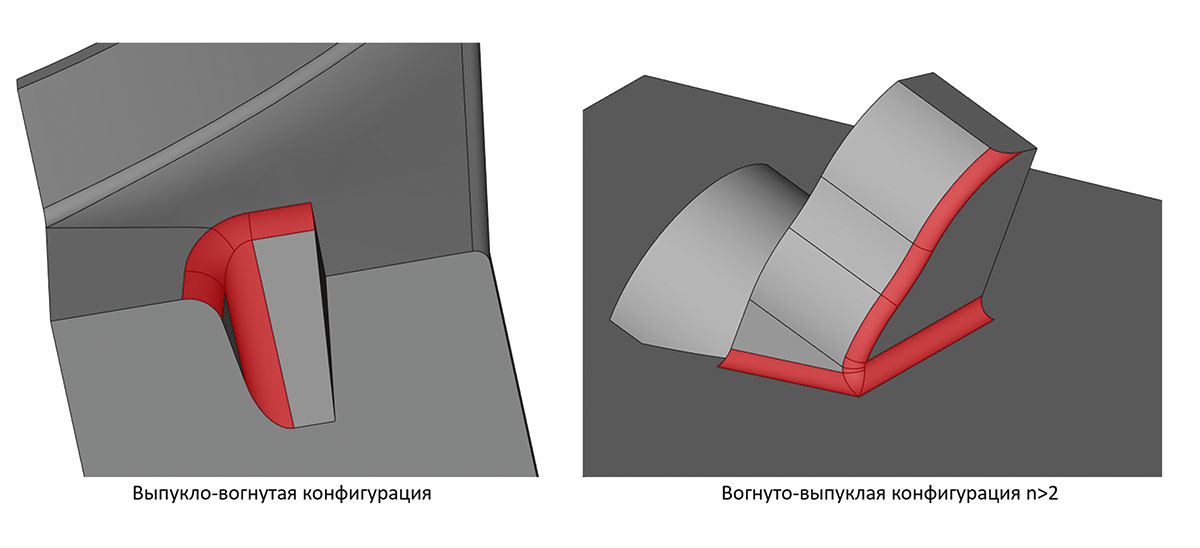
Рис. 51. Иллюстрация новых возможностей RGK в «трехреберной» обработке
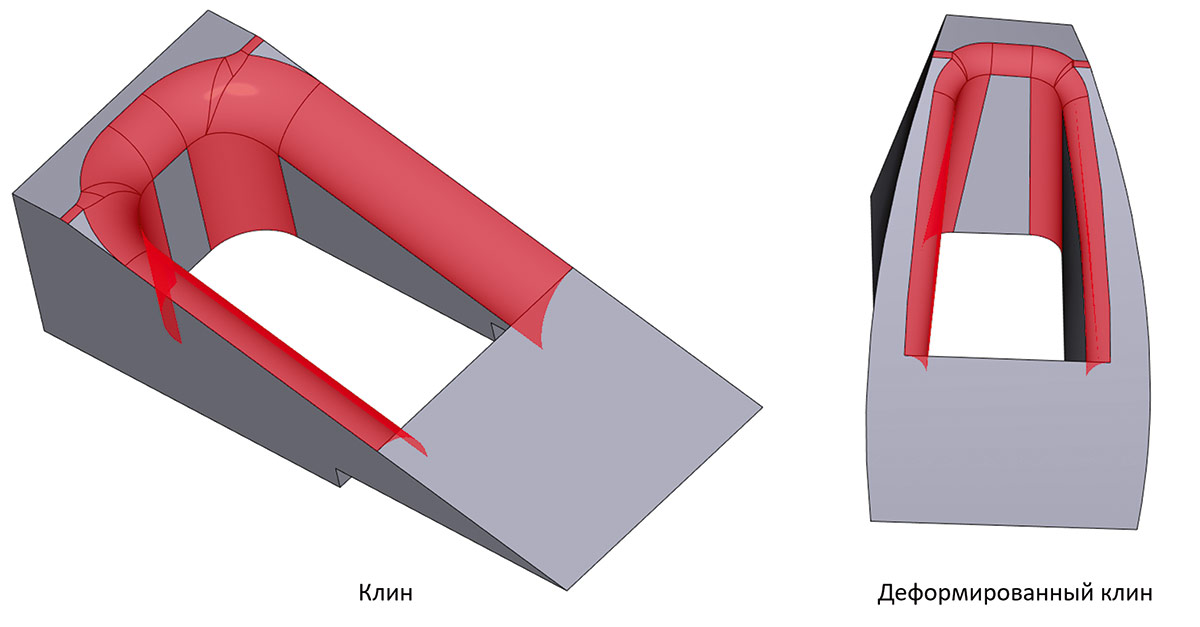
Рис. 52. Иллюстрация возможностей «четырехреберной» обработки (тело справа — с аналитическими поверхностями, а слева — тело той же топологии, но со сплайновыми гранями и более грубой точностью топологии)
Рассмотрим еще ряд улучшений топологических алгоритмов сглаживания. Нередко возникают ситуации, когда сглаживаемые грани в одной своей области трансверсальны, а в другой — практически касаются друг друга. Бывают также ситуации, когда конфигурации граней имеют так называемую «переменную» выпуклость — одна часть выпуклая, а другая вогнутая. Такие случаи являются вызовом для любого геометрического ядра. Если еще добавить, что сглаживаемые ребра могут иметь разные точности, то, становится понятно, что стоит задача корректного учета как входных точностей модели, так и особенностей задачи с «неприятной» постановкой, о которых упоминалось в первой части статьи (см. «САПР и графика», № 6’2025). На рис. 53 приведено несколько наглядных примеров того, что умеет новая версия RGK.
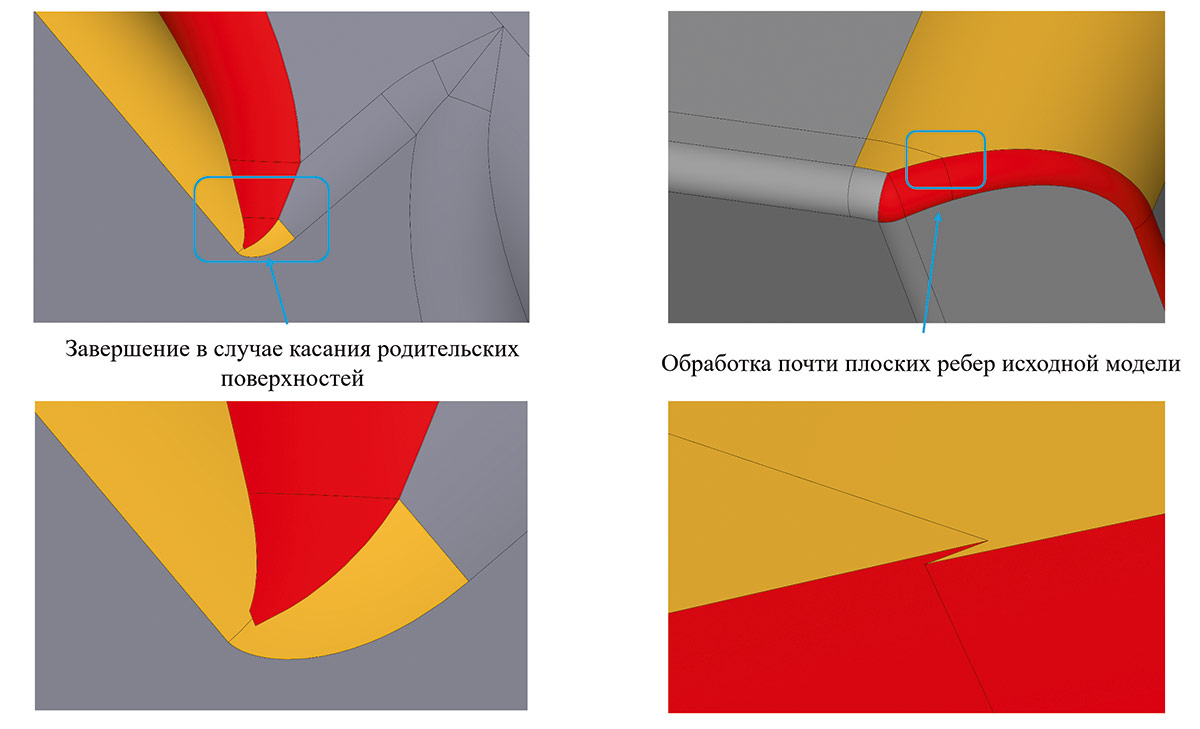
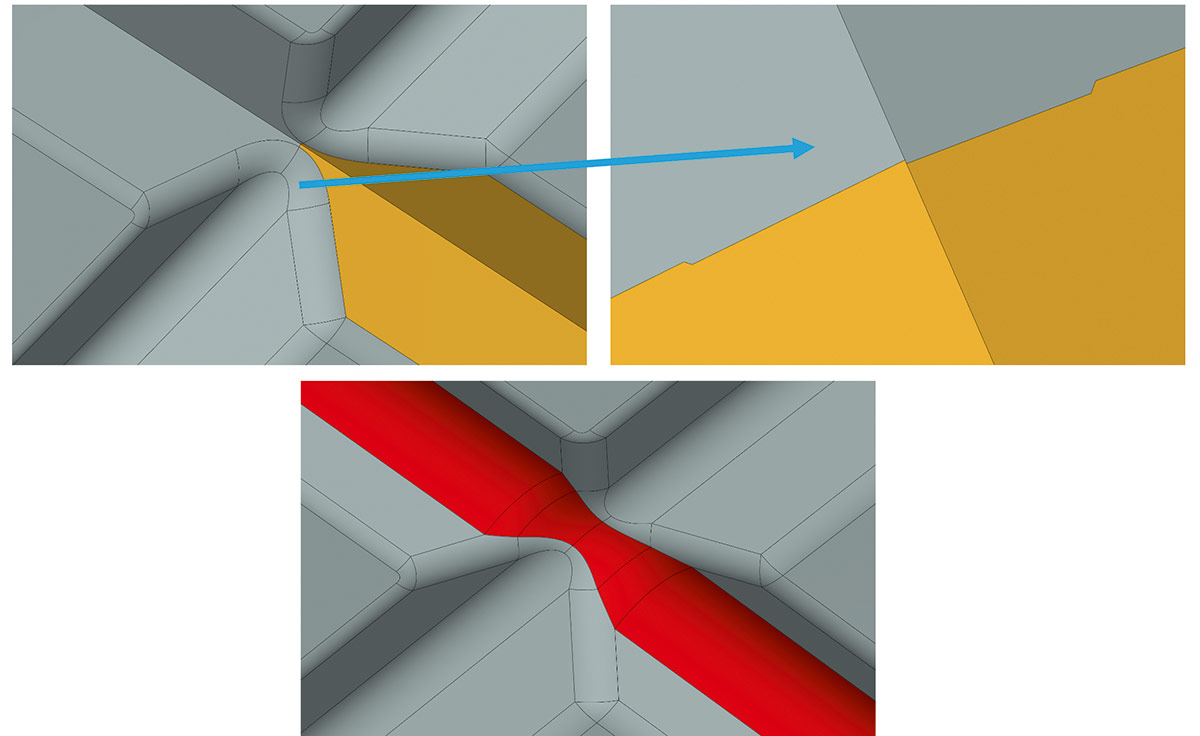
Рис. 53. Примеры работы RGK в областях с «неприятной» структурой
Примером задачи такого рода является сглаживание с касанием листов сглаживания или выходом на границы граней. То есть показана ситуация, когда еще нет переполнения и корректировки геометрии, сглаживающей поверхности в связи с изменением опорной геометрии, но сглаживаемая грань уже перекрывается сглаживанием полностью или частично. В таком случае тоже надо понимать, что точность ребер, которые становятся границей сглаживания, может быть разной (рис. 54).
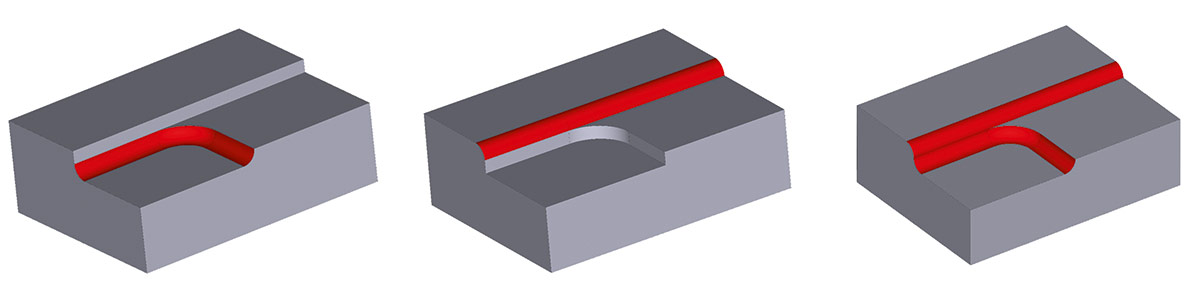
Рис. 54. Пример корректной работы алгоритмов RGK новой версии в «пограничных» случаях (приведен случай на фрагменте реальной модели, где сглаживаемые грани представляют собой сплайновые поверхности)
Дальнейшей доработке подвергся механизм встраивания сглаживающих листов в тело. Теперь он позволяет строить модели с конфигурацией топологии, доступные не всем системам так называемого «тяжелого» класса (рис. 55).
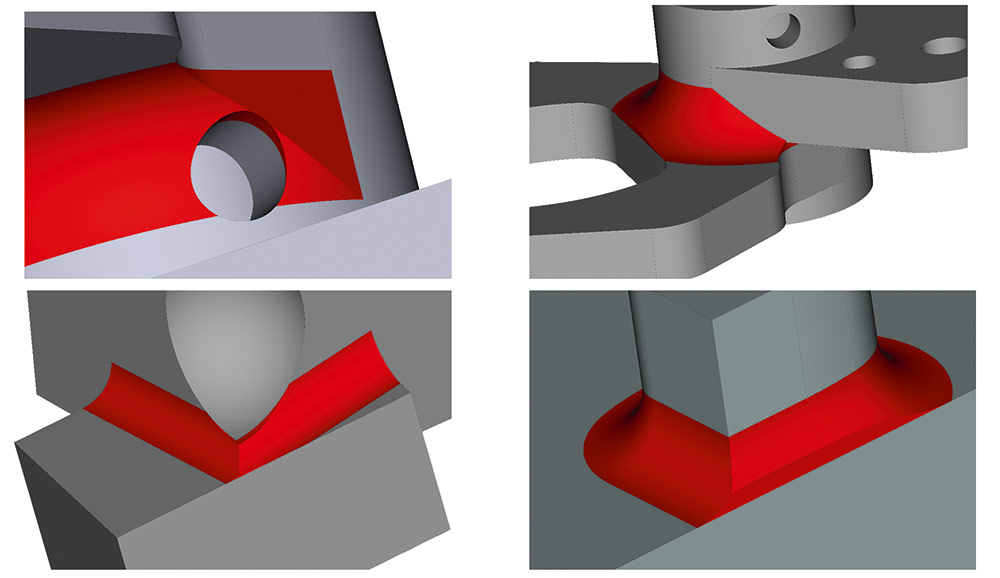
Рис. 55. Примеры работы нового алгоритма встраивания сглаживания
Развитие также получила функциональность по остановке сглаживания по требованию, которая была представлена в предыдущих версиях. Сейчас функциональность стала гораздо более мощной (рис. 56).
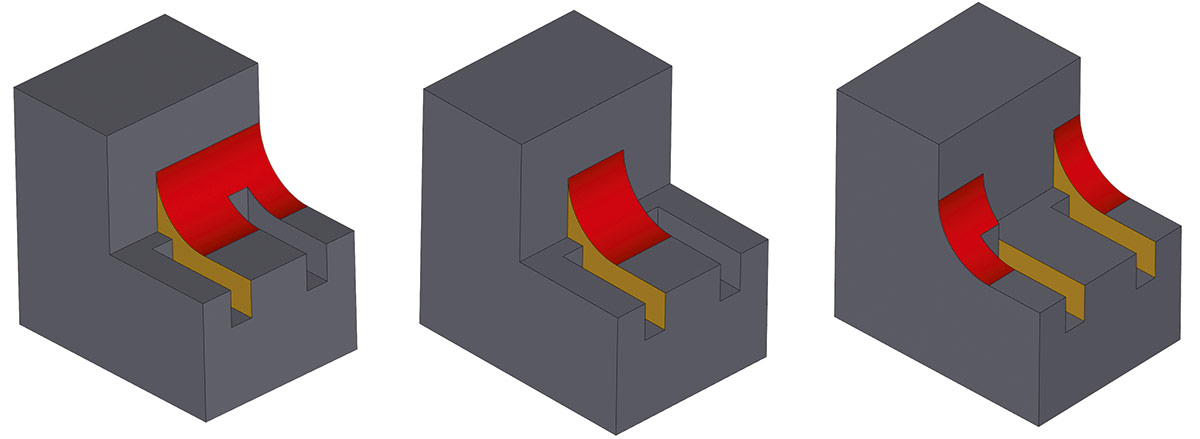
Рис. 56. Пример работы функциональности остановки сглаживания по выбранной топологии тела
Особого рассмотрения заслуживает развитие математики поверхностей для решения различных сложных задач «заполнения области». Об этом классе алгоритмов, которые развиваются в RGK, было объявлено в предыдущей версии. С тех пор в качестве результатов был достигнут значительный прогресс. Следует отметить, что для его получения потребовалось гораздо больше времени и усилий, чем первоначально предполагалось, по развитию уникальной математики поверхностей приближения, которая находит применение в разных частях ядра. Кроме того, следует отметить, что работа в этой области продолжается, но уже в новой версии эти алгоритмы включены в различные обработки, которым они соответствуют. Рассмотрим более подробно, о каком инструменте идет речь. При моделировании часто возникает потребность построить поверхность, которая бы аппроксимировала заданный контур (набор кривых) с заданной точностью, при этом обеспечивала бы гладкое (в смысле G1 или G2) сопряжение с поверхностями, граничащими с границами контура. Другой вариант задачи предполагает возможность задания кривых и точек внутри области затягивания. Существует задача замены набора гладко сопряженных граней одной поверхностью с требуемой степенью гладкости. Есть еще целый ряд родственных постановок. В частности, пресловутая задача формирования «чемоданного угла» в сглаживании и ее обобщение. Во всех современных промышленных ядрах для решения указанных задач исторически используются разные техники построения поверхностей. Однако наиболее общим механизмом является алгоритм построения поверхности приближения, близкий по идеям к физическим моделям тонких деформируемых пластин. Тут нужно указать, что вообще-то речь идет не о компактном алгоритме, который формально решает задачу, а скорее о семействе параметрически управляемых алгоритмов, которые на выходе формируют поверхность требуемого качества. Этим фактом и обусловлена большая математическая и программная сложность реализации такого подхода в ядрах. Вместе с тем мощность математики, которая стоит за этим, позволяет решить целый спектр задач поверхностного моделирования. На рис. 57 приведены примеры работы таких алгоритмов в новой версии RGK.
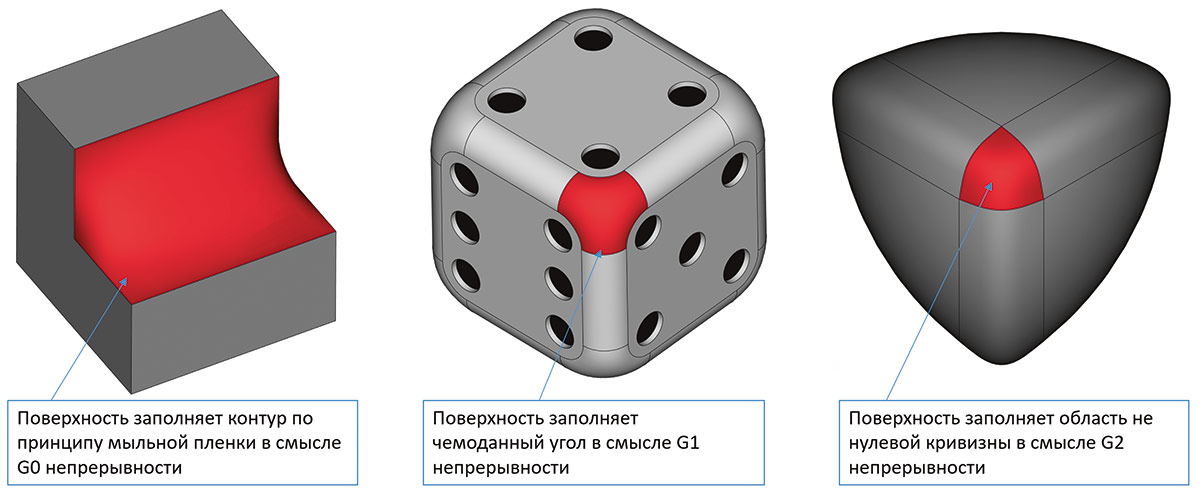
Рис. 57. Примеры поверхностей приближения при заполнении областей с разной степенью гладкости на границе
Более подробно рассмотрим случай формирования поверхности приближения на «неприятной» задаче приближения «ломаного» каркаса (рис. 58).

Рис. 58. Пример построения поверхности (слева — исходный контур с изломом, дальше гладкая поверхность, которая приближает его с заданной точностью)
Понятно, что пример на рис. 5 (см. «САПР и графика», № 6’2025) довольно надуманный, но он иллюстрирует устойчивость алгоритма даже к «неприятным» постановкам. На рис. 59-62 приведены примеры решения практически более значимых задач.

Рис. 59. Пример G1 гладкого заполнения области невыпуклой формы с соблюдением касания с соседними гранями
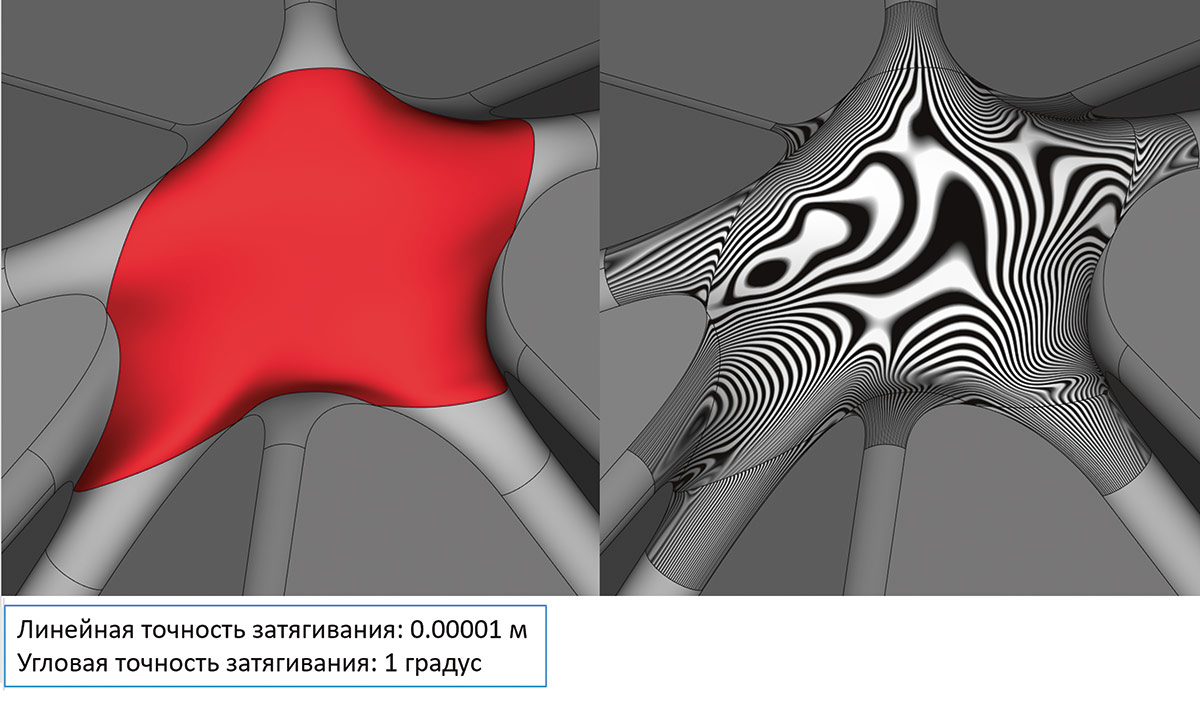
Рис. 60. Пример затягивания области типа «неправильная звезда» с соблюдением G1 гладкости на границах
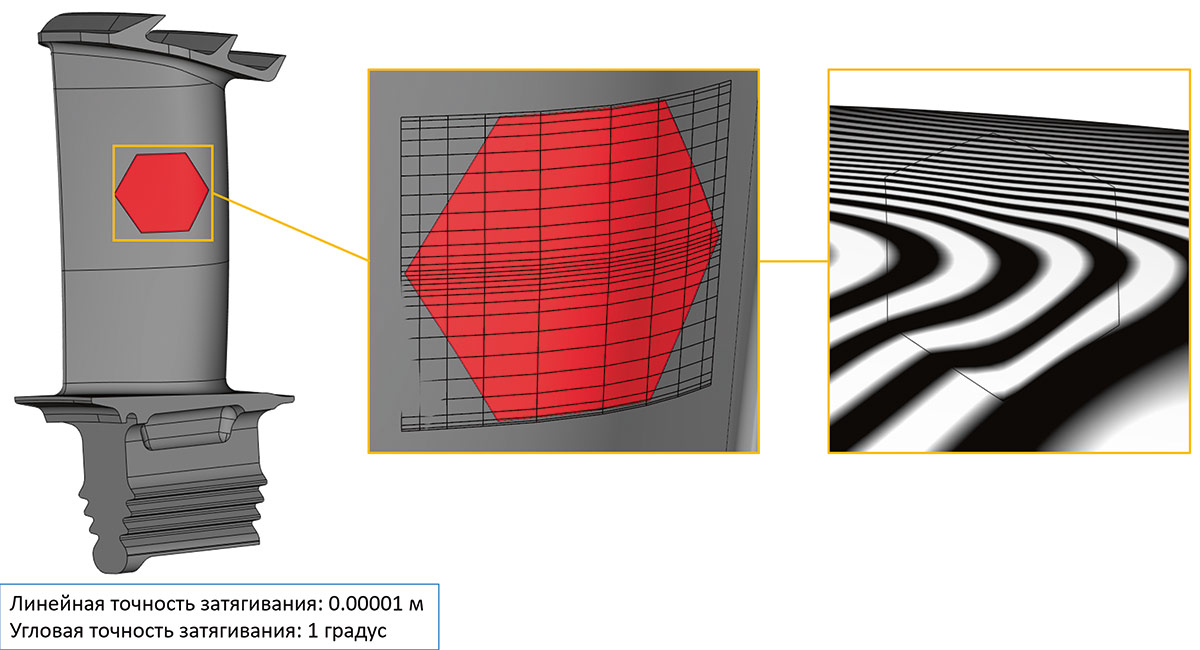
Рис. 61. Пример заполнения шестиугольной области по G2-условию через границу
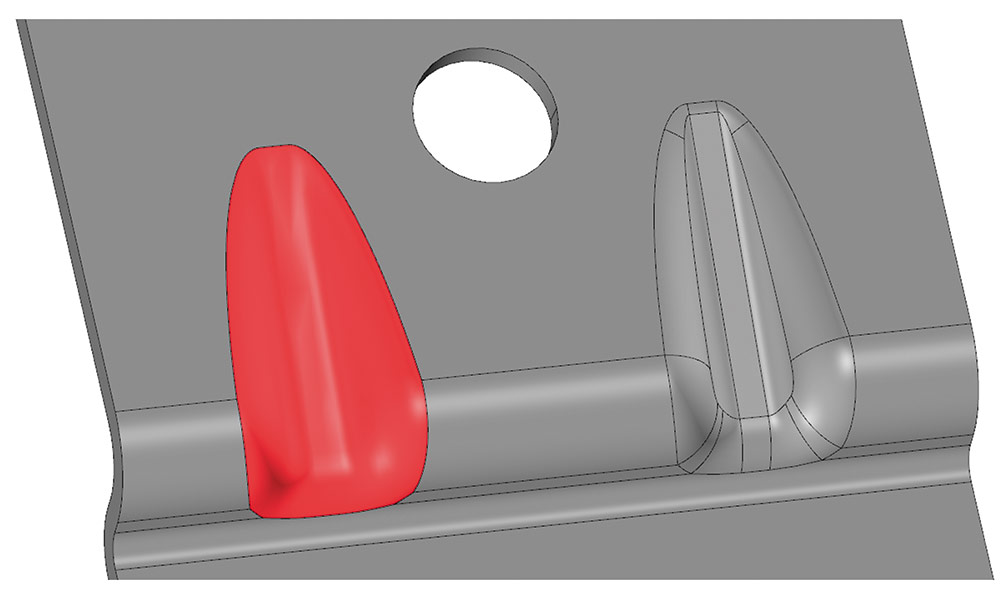
Рис. 62. Пример применения алгоритма приближения в задаче замены набора гладко сопряженных граней поверхностью с соблюдением гладкости через границы
В завершение обзора алгоритма приближения поверхностей хочется рассказать об использовании инструментов RGK в новой версии T-FLEX CAD 18 для решения важной прикладной задачи. Речь идет о задаче построения так называемой поверхности «грубого смещения». Дело в том, что в автомобильной промышленности при проектировании кузова автомобиля возникает необходимость построения поверхности, эквидистантной набору граней с большим смещением — таким, что эквидистанта в обычном смысле не существует из-за «схлопывания» топологий и самопересечений. Это пример сугубо прикладной задачи геометрического моделирования, которую нельзя отнести к функциональности общего применения и решение которой нет смысла добавлять в ядро как отдельный генератор. Но ее можно решить, используя инструменты ядра. В качестве референса здесь мы используем аналогичную функциональность CATIA v5. Итак, покажем наглядно, в чем состоит эта задача.
Как видно на приведенном рис. 63, задача не может быть решена традиционной функциональностью геометрических ядер из-за фактически полного вырождения топологий на больших величинах смещения. Также следует заметить, что требования по точности аппроксимации результата в данной задаче невысоки — требуется построить «спокойную» поверхность, примерно повторяющую форму исходного листового тела. Применение математики RGK дало возможность решить эту задачу в рамках проекта T-FLEX CAD 18 (рис. 64 и 65).
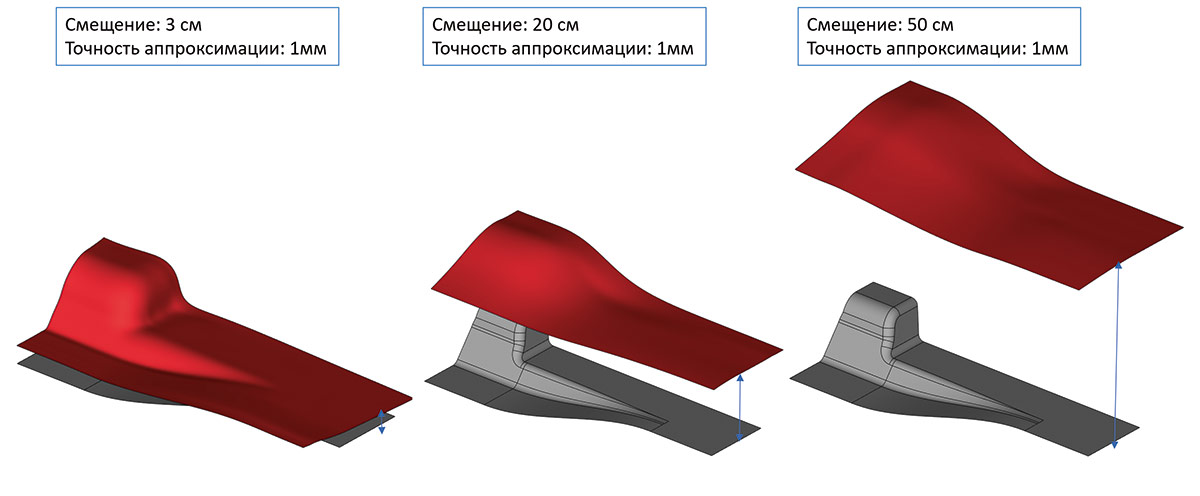
Рис. 63. Иллюстрация постановки задачи построения поверхности «грубого смещения» (серым цветом показано исходное листовое тело, а красным — результирующая сплайн-поверхность смещения)
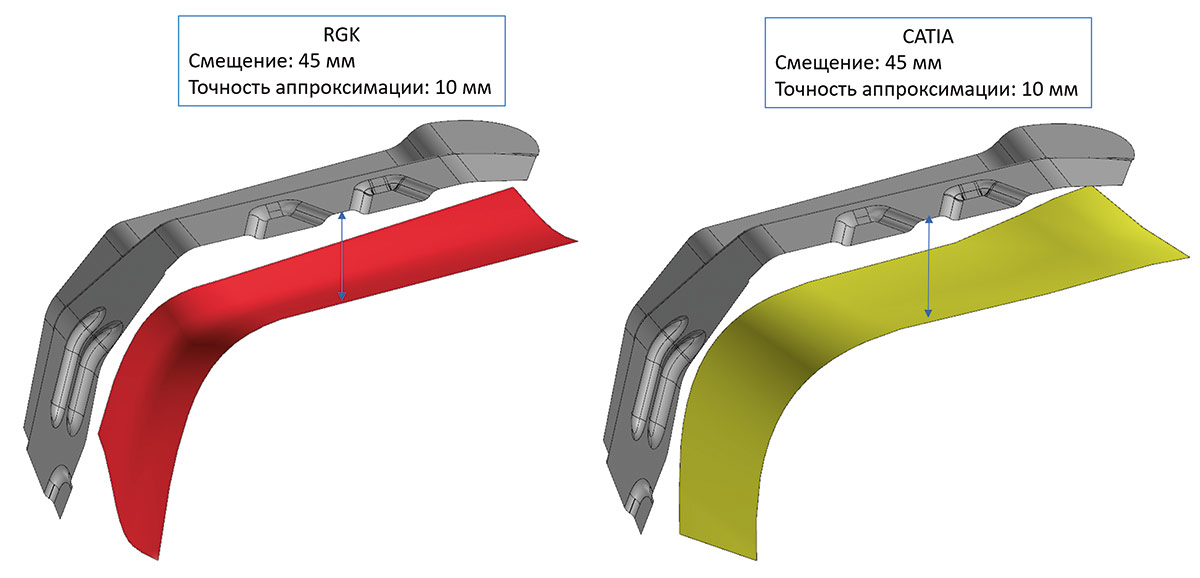
Рис. 64. Пример применения функциональности «грубого смещения» на реальной модели в сравнении с конкурирующим решением (следует обратить внимание, что результат в T-FLEX CAD несколько точнее)
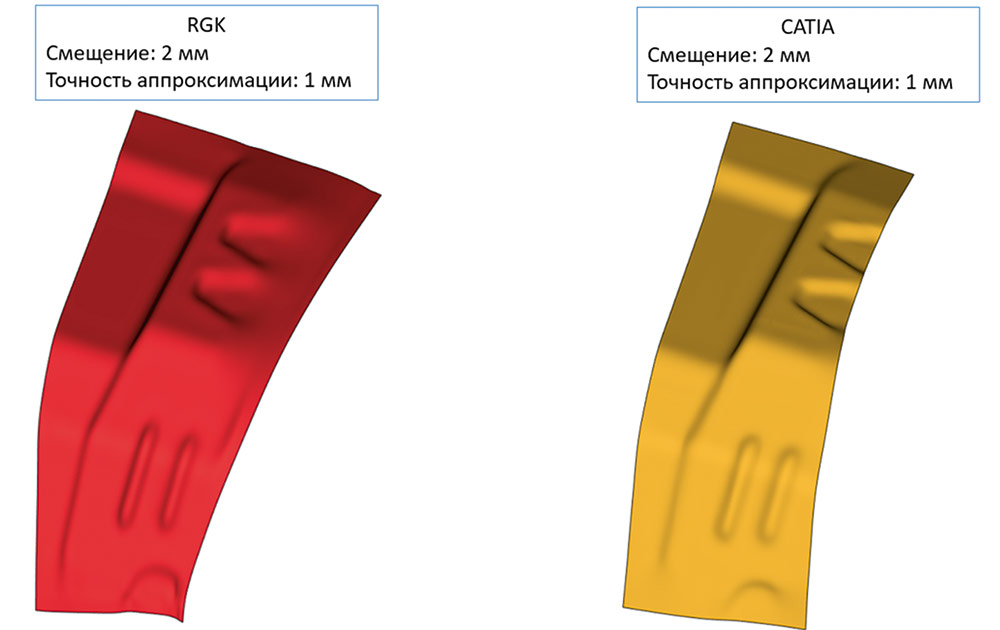
Рис. 65. Пример работы алгоритма на меньшем смещении
Еще раз обратим внимание, что показанный пример — это демонстрация использования технологий RGK в рамках проекта T-FLEX CAD 18, а не функция самого ядра. Это важный момент, иллюстрирующий тот факт, что разработчики RGK очень аккуратно подходят к составу API ядра, не перегружая его прикладными функциями, которые не требуются большинству приложений. В результате, API не «раздувается», но обеспечивает необходимый инструментальный базис для всех областей применения. Это важный принцип разработки ядра в качестве универсального промышленного инструмента для использования в широкой гамме приложений. Такой достаточный минимализм стал возможен, поскольку RGK изначально разрабатывалось как универсальное ядро на основе многолетнего опыта применения промышленных геометрических ядер, а не как рефакторинг внутренних алгоритмов той или иной прикладной системы. Кстати говоря, исходная модель была получена путем импорта через формат STEP, транслятором, входящим в расширенную поставку RGK.
Помимо совершенствования уже существовавших в предыдущих версиях инструментов, разработан ряд новых генераторов. В частности, была проделана большая работа по созданию генератора построения срединных тел. Эта важная для расчетных приложений функциональность ранее не была доступна в RGK, но с выходом новой версии ядра появилась в API. Следует предварительно пояснить, что это за функциональность и почему ей в новой версии было уделено серьезное внимание. Дело в том, что при построении расчетной модели так называемых «оболочечных» конструкций важно уметь заменить тонкостенное твердое тело поверхностным телом, грани которого будут находиться внутри и, в некотором смысле, «посередине» граней исходного тела. «Срединность» обычно понимается по крайней мере в трех смыслах (рис. 66).
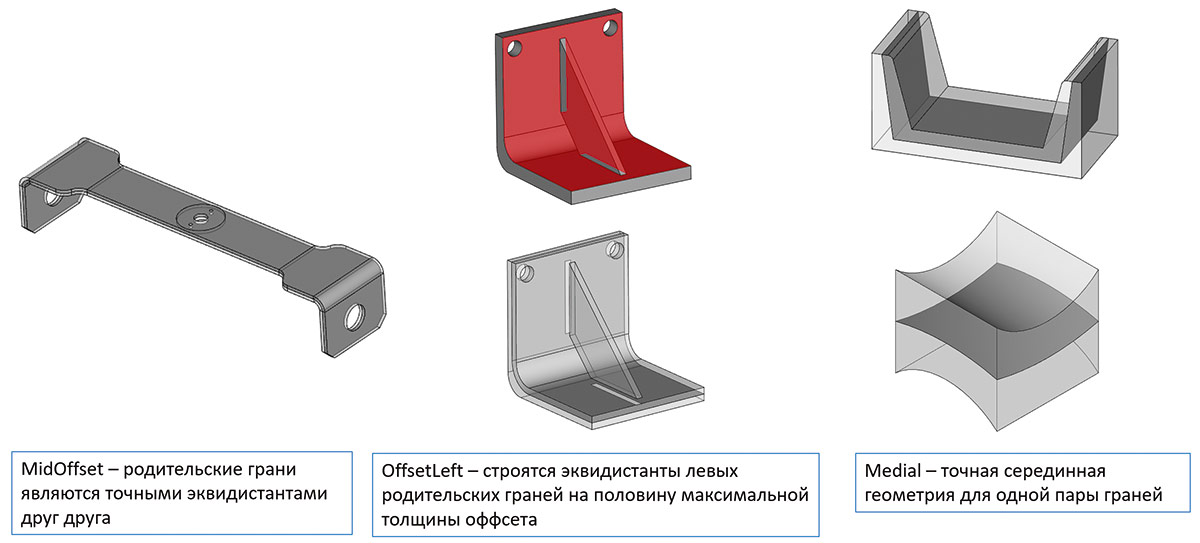
Рис. 66. Пояснение трех различных интерпретаций срединной поверхности в RGK
Понятно, что наиболее типичный способ — это интерпретировать срединную поверхность именно как простую эквидистантную к заданной паре поверхностей. Но это возможно не всегда. А именно только тогда, когда соответствующая пара граней сама содержит поверхности, эквидистантные друг другу. В иных случаях используются другие интерпретации. В том числе и формально точное: поверхность, каждая точка которой равноудалена от двух заданных поверхностей. Для построения такой поверхности требуется решать некоторые уравнения. Но построением самой поверхности задача не ограничивается. Так как исходное тело содержит больше одной пары граней, требуется построить грани нового листового тела для каждой «эквидистантной» пары и потом увязать такие грани между собой для формирования корректного поверхностного тела. Этот результат достигается за счет нескольких последовательных шагов.
Как можно заметить из представленных иллюстраций (рис. 67 и 68), возможен ответ в виде как набора отдельных связанных листовых тел, так и non-manifold листового тела — в зависимости от потребностей приложения. Новый инструмент уже сейчас оснащен довольно мощными практическими опциями. Так, например, доступна возможность автоматического удаления сглаживаний (рис. 69).
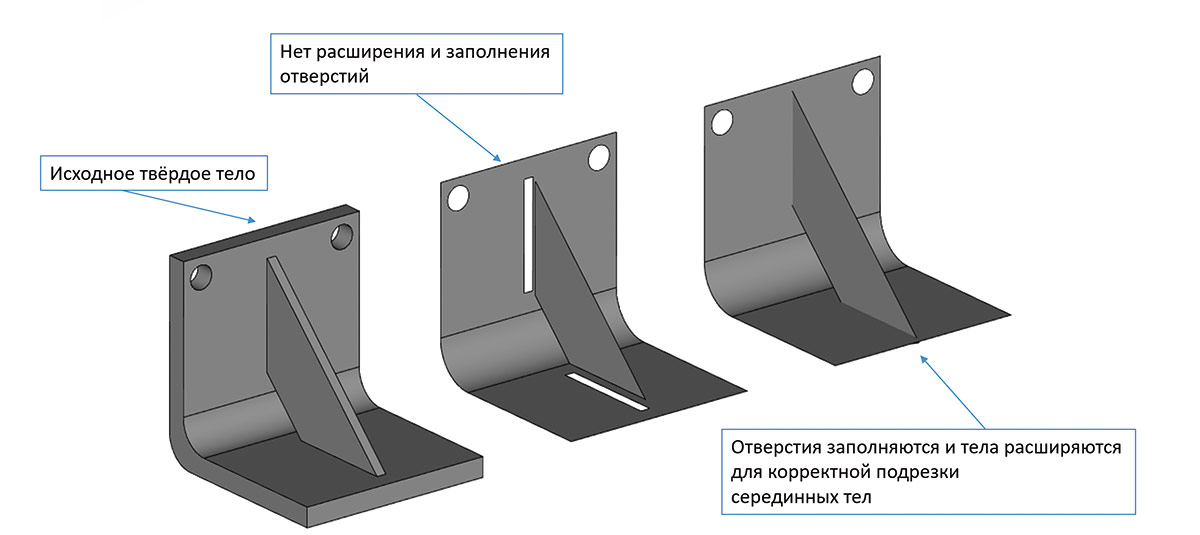
Рис. 67. Процедура формирования срединного листового тела
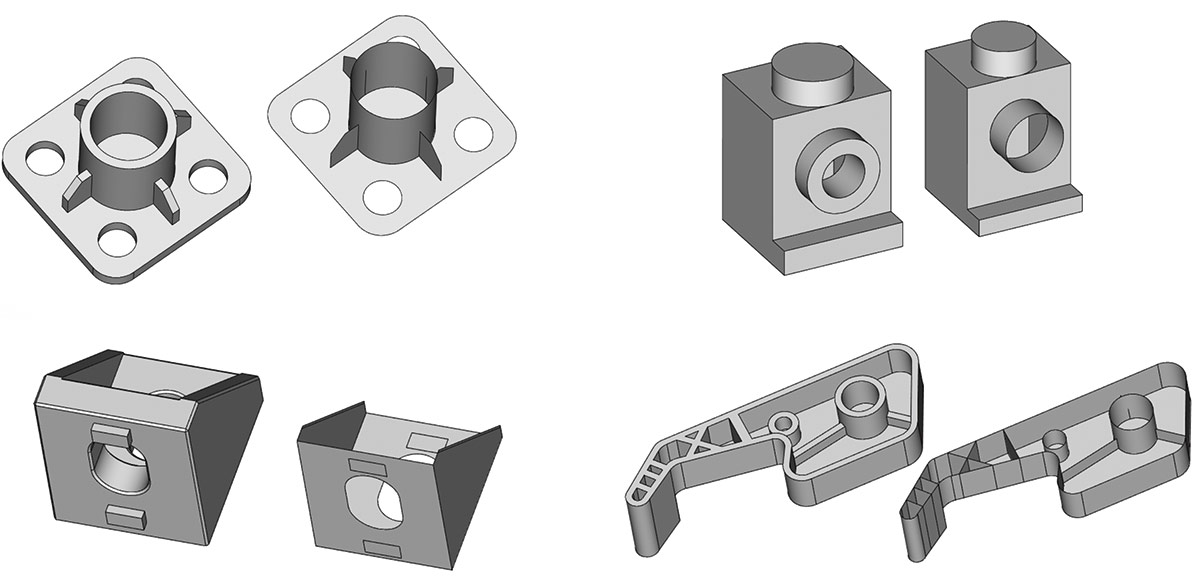
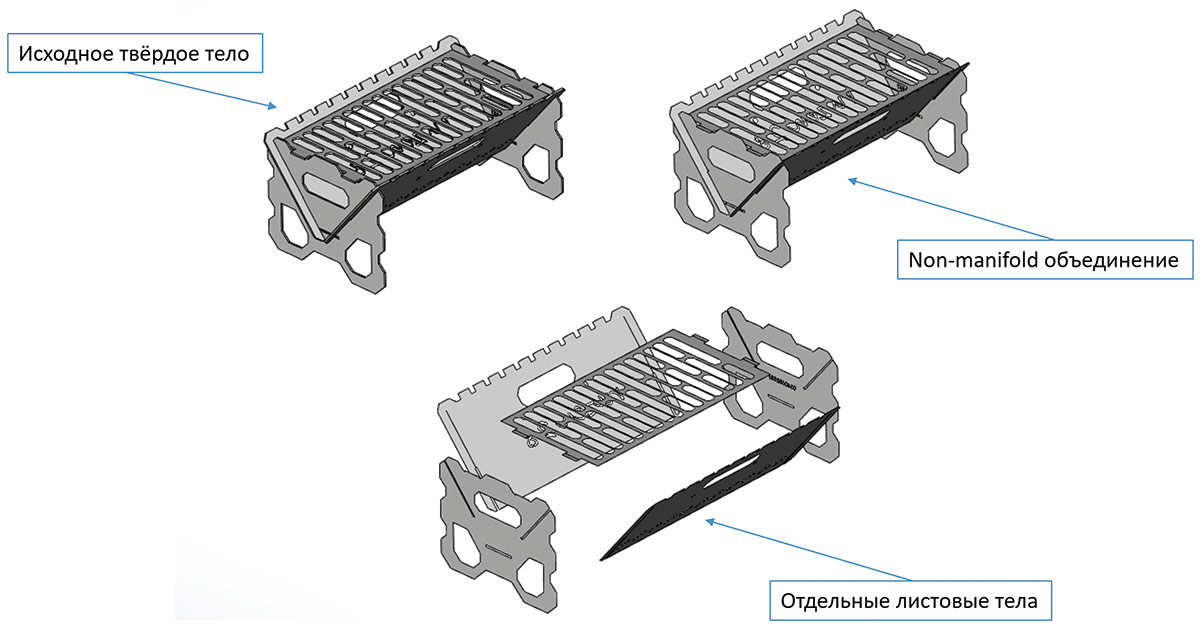
Рис. 68. Примеры формирования листовой модели для тонкостенных твердых тел
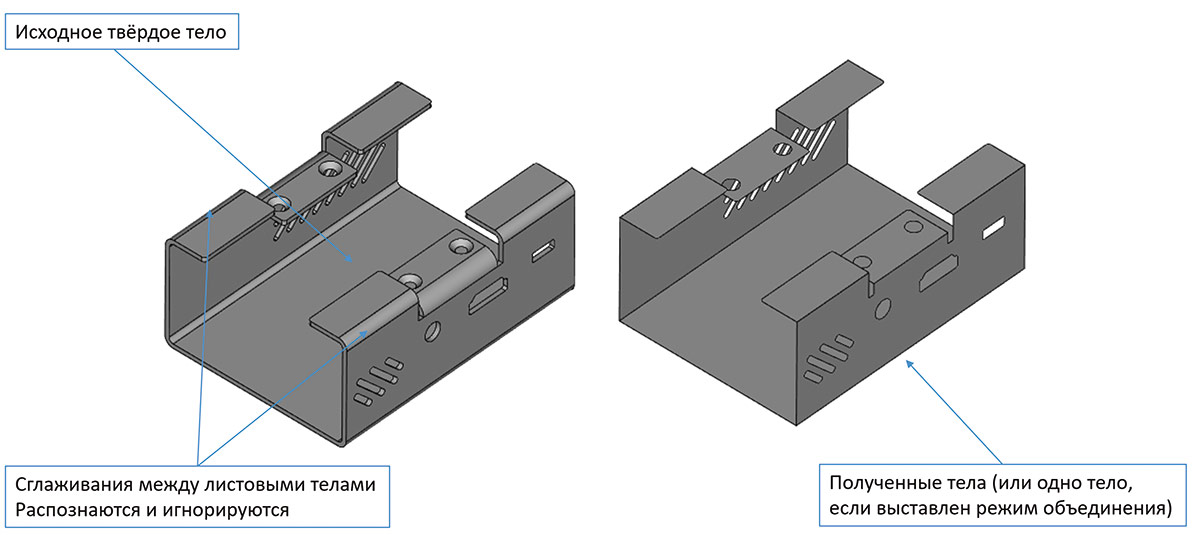
Рис. 69. Построение срединного тела с автоматическим удалением сглаживаний
Еще одной новой функциональностью ядра стали инструменты по разделению тела на области по изоклинам и вычислению теней между телами. На рис. 70-72 приведены примеры работы названных инструментов.
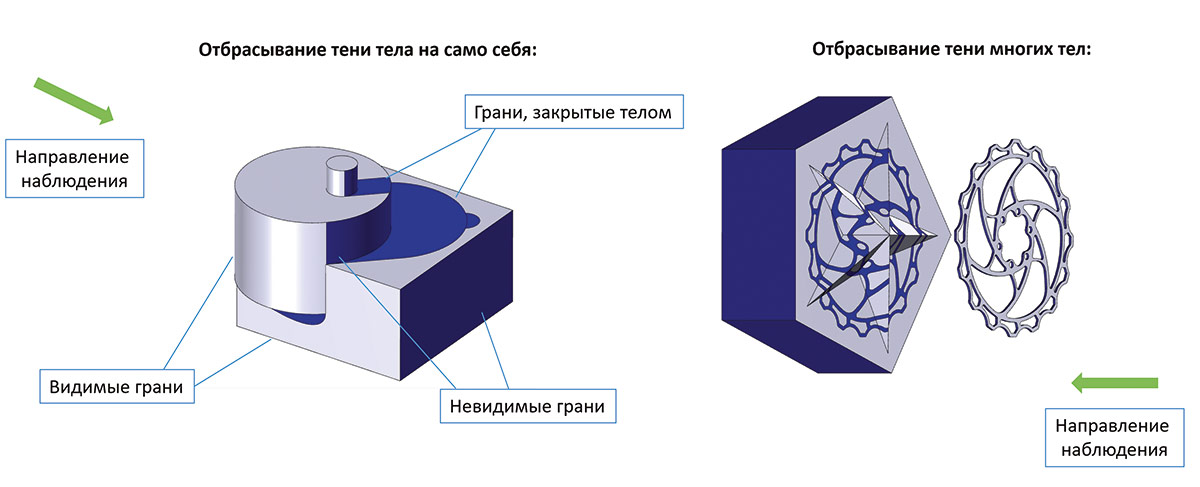
Рис. 70. Примеры работы генератора теней на точной модели тела в случае параллельной проекции
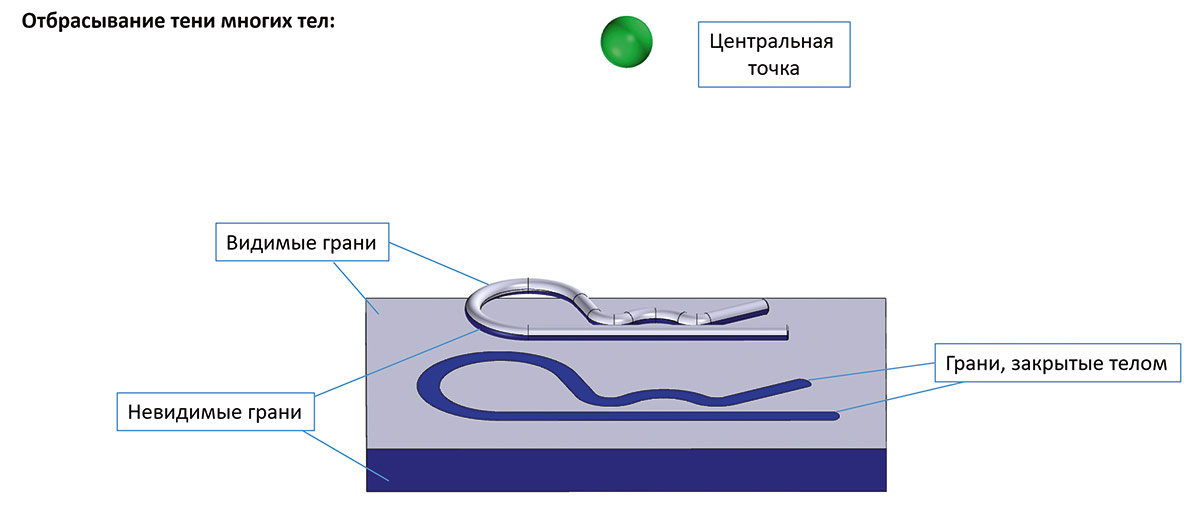
Рис. 71. Пример работы генератора теней на точной модели тела в случае центральной проекции
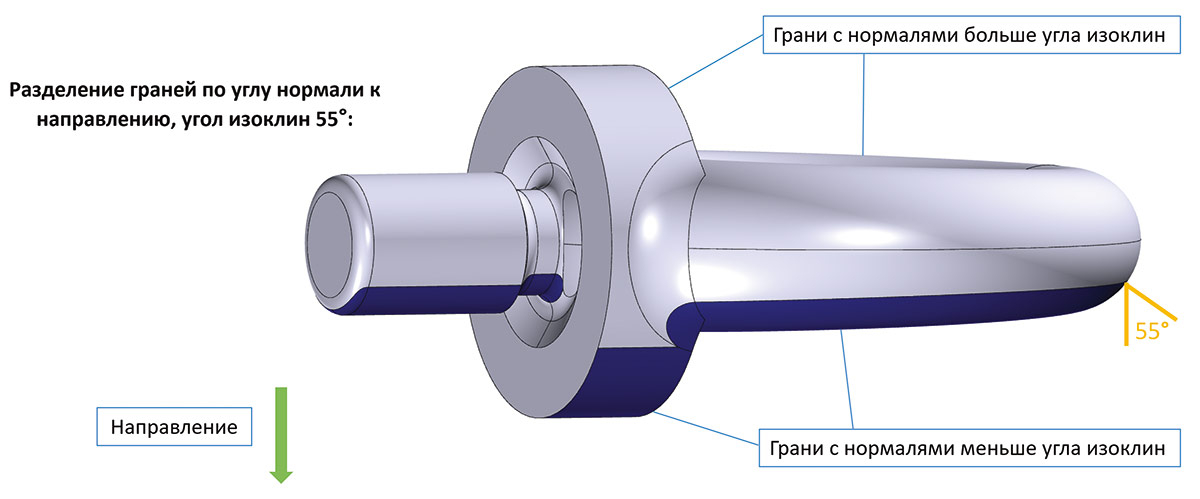
Рис. 72. Пример разделения тела изоклинами с заданным углом уклонения нормалей
При работе с проволочными телами (кривыми) добавилась возможность построения эквидистанты к кривой по поверхности, на которой она лежит, и построения листового тела как смещения кривой в две стороны (рис. 73).
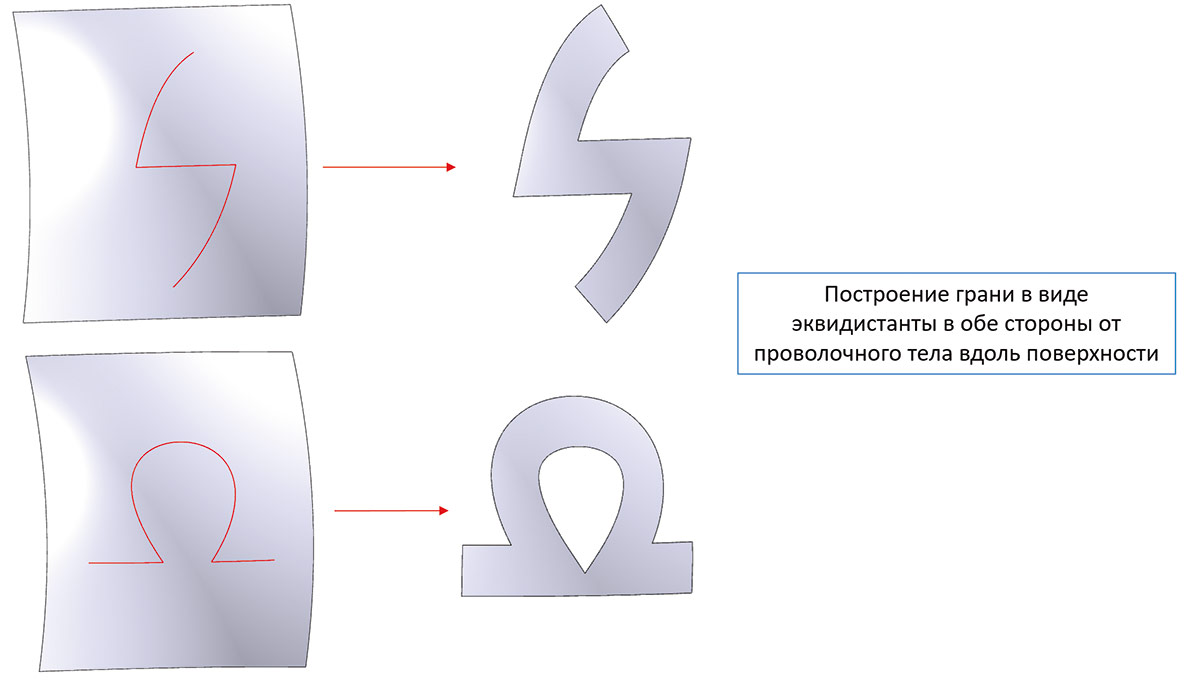
Рис. 73. Пример построения поверхностного тела путем построения эквидистанты заданной кривой с обработкой углов и самопересечений
Улучшения в функциональности анализа модели
Дальнейшие улучшения проведены в алгоритмах расчета параметров модели. В частности, площади поверхности и объема тела. Теперь возможно получение таких параметров с высокой точностью в случае определенных классов геометрии. Более конкретно поддерживается:
- плоскость, ограниченная прямыми, окружностями и эллипсами;
- сфера, ограниченная окружностями любого радиуса;
- цилиндр, конус и тор, ограниченные своими изолиниями.
Например, для тел, приведенных на рис. 74, объем и площадь могут быть подсчитаны с точностью машинного округления.
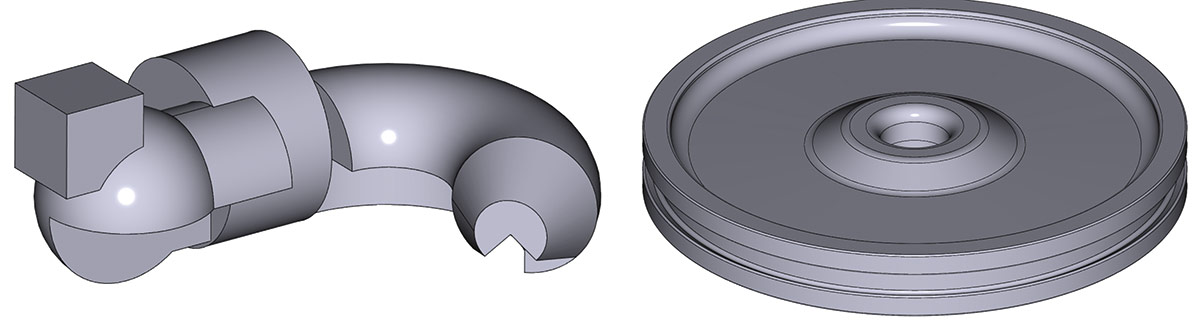

Рис. 74. Пример тел, площадь поверхности и объем (для верхних тел), которых сейчас рассчитывается точно
Изменения в построении проекций моделей с удалением невидимых линий на плоскость
Значительное внимание в новой версии ядра было уделено совершенствованию алгоритмов построения проекций моделей на плоскость. Была существенно улучшена точность вычисления проекций и корректность алгоритмов удаления невидимых линий. Также был разработан режим центрального (перспективного) проецирования — опция, ранее недоступная в RGK. Несмотря на то что на практике эта функциональность востребована гораздо меньше, чем параллельное проецирование, для некоторых случаев она может быть полезна, поэтому было принято решение о ее добавлении в ядро (рис. 75 и 76).
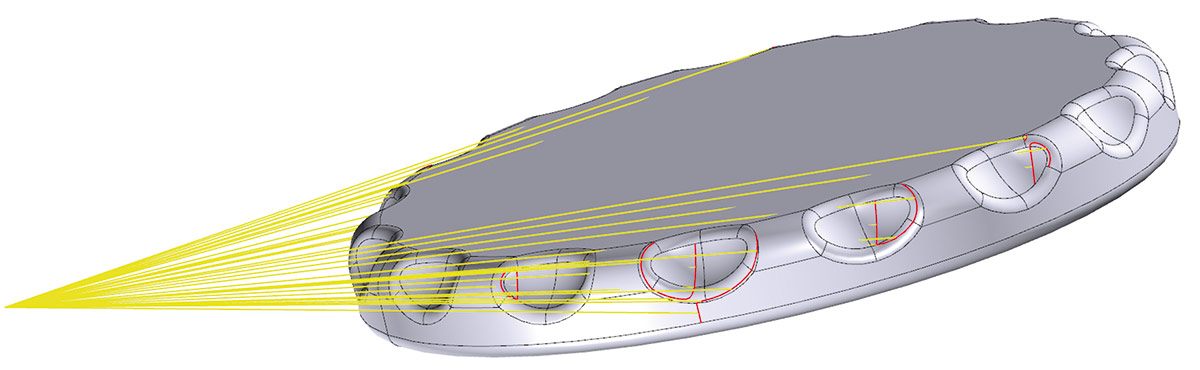
Рис. 75. Иллюстрация отличия построения очерковых линий на модели при центральном проецировании
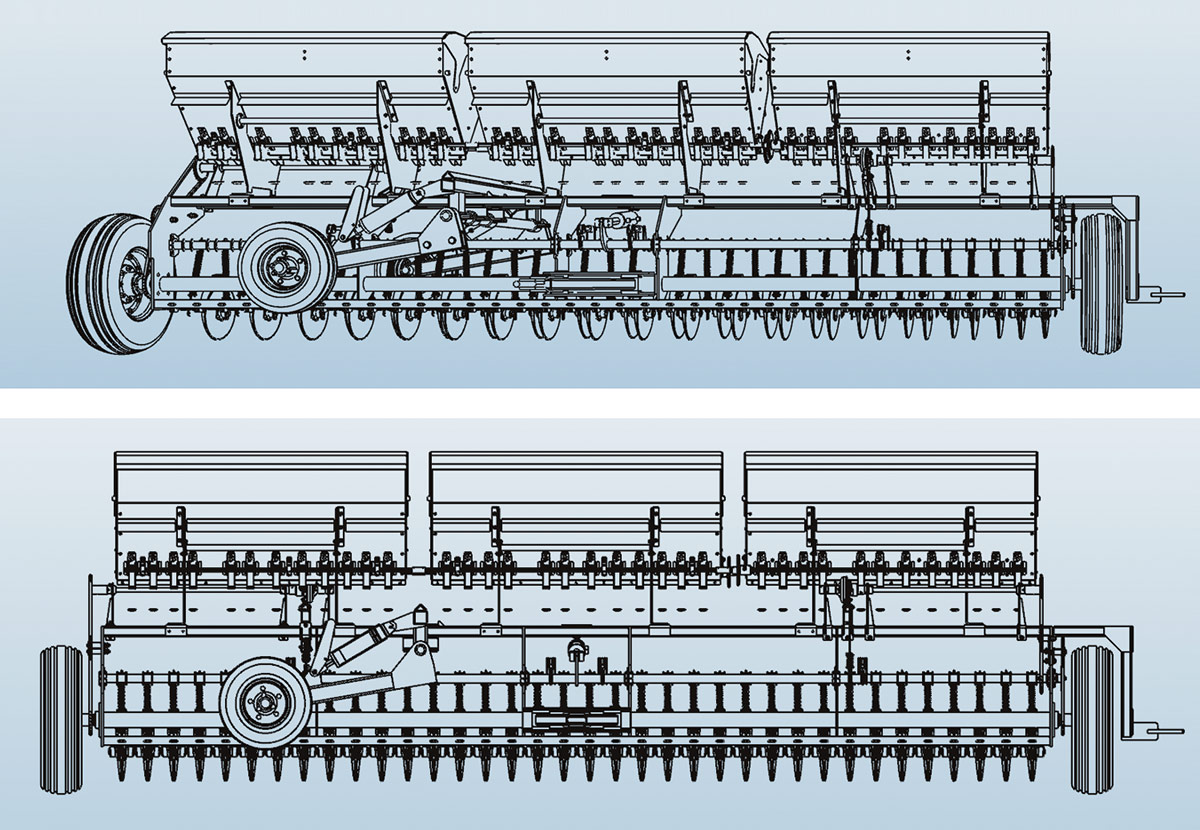
Рис. 76. Иллюстрация работы алгоритма проецирования с удаленными невидимыми линиями (снизу — вид параллельного проецирования, сверху — вид центрального проецирования: видно перспективное искажение проекции)
Улучшение в работе алгоритмов триангуляции
Не осталось без внимания и развитие такой важной функциональности, как построение полигональной модели — триангуляция B-rep. Завершена работа по унификации базовых алгоритмов разбиений и оптимизации структур данных. Это позволило примерно вдвое сократить требования по оперативной памяти в процессе триангуляции, обработать сложные случаи самопересечений циклов на гранях, уменьшить размеры получаемых сеток с сохранением точности, поднять общую производительность алгоритмов. На рис. 77 приведены несколько примеров, иллюстрирующих текущий прогресс.
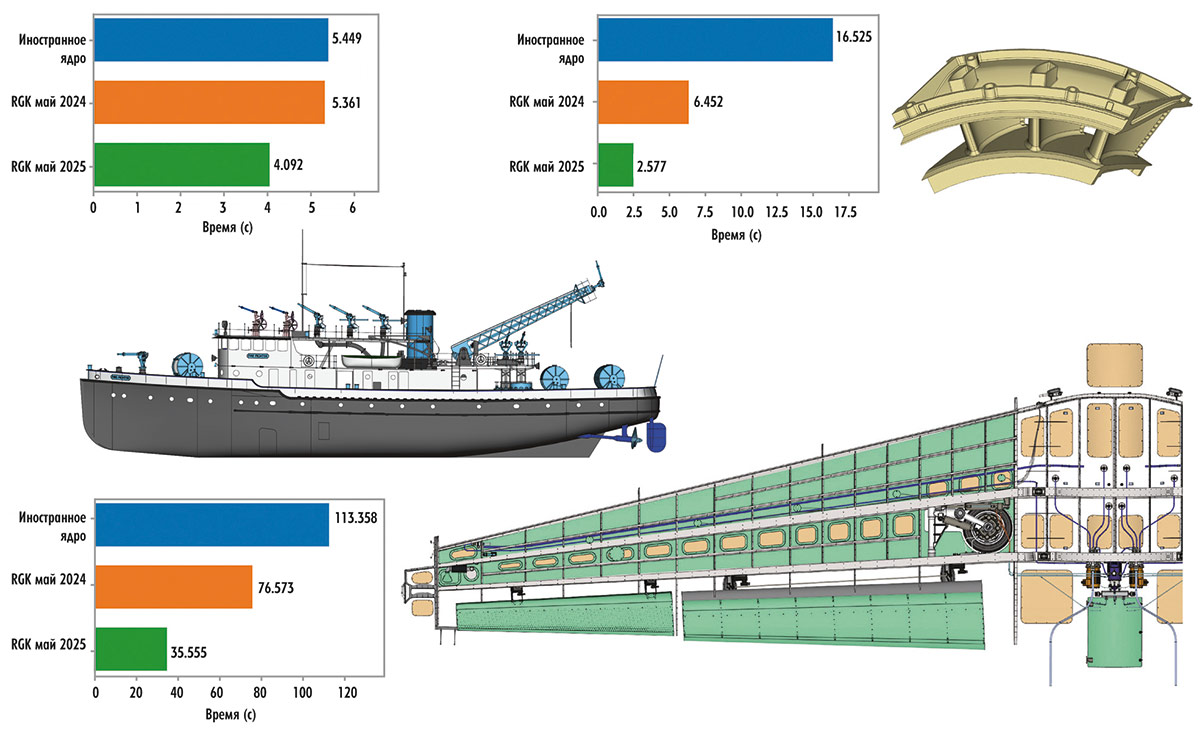
Рис. 77. Примеры работы триангулятора RGK текущей версии в сравнении
с предыдущей и известным промышленным ядром
В алгоритмы триангулятора был добавлен важный для приложений режим игнорирования мелких топологических элементов. Эта функциональность важна как для задач упрощения геометрии при подготовке расчетных моделей, так и для упрощения сеток при визуализации моделей с насыщенной мелкой топологией в задачах работы со сборочными моделями сложных изделий (рис. 78).

Рис. 78. Пример работы новой функциональности по игнорированию мелких элементов
Следует отметить, что в новой версии триангулятор поддерживает корректную работу с обобщенной топологией (рис. 79), о которой шла речь в первой части статьи (см. «САПР и графика», № 6’2025).
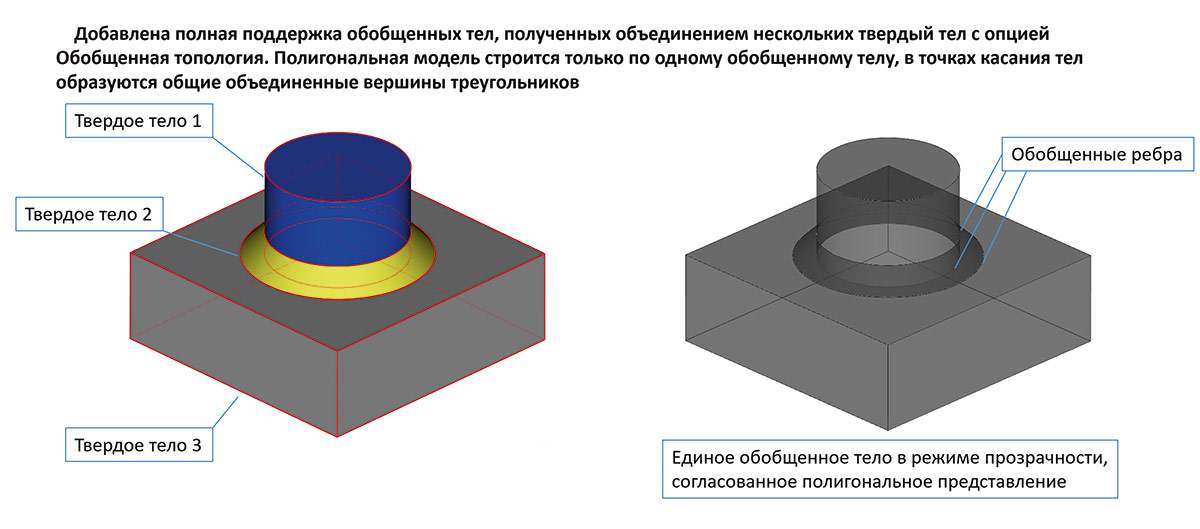
Рис. 79. Пример работы триангулятора на теле non-manifold, полученном объединением трех тел
Заключение
Ядро RGK год от года активно развивается. Постоянно расширяется его функциональность. Новая версия является важным этапом развития RGK, так как знаменует собой достижение значительной функциональной полноты решаемых задач. Можно утверждать, что с выходом новой версии RGK функционально готово к внедрению в системы инженерного проектирования и моделирования тяжелого класса. Конечно, совершенно очевидно, что предстоит большой объем работы по оптимизации алгоритмов, развитию различных опций и режимов, оттачиванию поведения математики во всевозможных сложных случаях. Однако это уже больше экстенсивная, но очень важная и трудоемкая работа. Предыдущий год разработки показал, что идеология и архитектура ядра полностью удовлетворяют задачам промышленных систем проектирования и служат надежным фундаментом разработки первого в нашей стране промышленного ядра тяжелого класса.
Подробнее смотрите на сайте: https://rgkernel.ru/



