Газодинамический расчет первой ступени экспериментального двухступенчатого компрессора с использованием программного комплекса CFX

Иван Воронич, Леонтий Ивчик, Владимир Коньшин, Владимир Ткаченко

Объект численных исследований

Построение расчетной сетки

Построение модели численного исследования

Учет трехмерной деформации лопатки под действием центробежных и газодинамических сил

Результаты расчетов и сравнение с экспериментом

Выводы и рекомендации

Прогресс в авиации во многом определяется уровнем развития двигателестроения — одной из важнейших отраслей промышленности, в которой сконцентрированы достижения фундаментальных и прикладных наук, высокие технологии проектирования и производства. Современные двухконтурные турбореактивные двигатели обладают довольно высокими характеристиками: так, КПД компрессора достигает 85-92%, а КПД турбины — 88-93%. Дальнейшее усовершенствование авиационных компрессоров идет по следующим направлениям: уменьшение количества ступеней за счет создания новых высоконапорных ступеней (с большей степенью повышения давления), увеличение КПД, снижение уровня шума, повышение запаса устойчивости. Решение этих сложных задач невозможно без детального знания трехмерной картины течения. Исследование режимов работы турбомашин в настоящее время является актуальной и сложной задачей. Применение компьютерного моделирования и систем автоматизированного инженерного анализа открывает новые возможности для совершенствования и оптимизации характеристик авиационных двигателей.

Кафедра компьютерного моделирования (ФАЛТ МФТИ), НТЦ им. А.М.Люльки (НПО «САТУРН») и инжиниринговая компания «ТЕСИС» провели исследование режимов работы первой ступени высокооборотного модельного авиационного компрессора. Для расчетов использовался программный комплекс аэродинамического анализа ANSYS CFX-5, который был установлен на вычислительном кластере МВС-1000/16. Средства CFX позволяют эффективно проводить расчет на многопроцессорных вычислительных системах. При проведении расчетов в системе распределенных вычислений МВС-1000/16 было достигнуто ускорение расчета до 12 раз. Получены основные характеристики работы компрессора в различных режимах и определена параллельная эффективность использования комплекса CFX на 16-процессорной вычислительной системе.

Объект численных исследований

Для построения математической модели был выбран модельный (уменьшенный) осевой компрессор низкого давления, разработанный и испытанный в НПО «САТУРН». Компрессор состоит из двух ступеней. Первая ступень состоит из входного направляющего аппарата (ВНА), рабочего колеса первой ступени (РК1) и направляющего аппарата первой ступени (НА1). ВНА состоит из 30 лопаток с симметричным профилем, РК1 — из 25 лопаток, НА1 — из 46 лопаток.

Частота вращения рабочего колеса составляет 28 тыс. об./мин. Рабочей средой является воздух. Исследовался ряд режимов работы ступени с различными степенями повышения полного давления.

Трехмерная модель компрессора была построена в системе Unigraphics (рис. 1).

Построение расчетной сетки

В качестве расчетной области для каждого венца выбиралась периодическая часть, содержащая одну лопатку.

Для построения сеток вокруг лопаток различных венцов в проточной части первой ступени компрессора использовалась программа CFX TurboGrid.

Для построения сетки применялся шаблон Generic Multi-Block Grid в CFX TurboGrid, который предполагает построение многоблочной О-сетки около поверхности лопатки и многоблочной Н-сетки в межлопаточном канале, областях вверх и вниз по течению. Построенные расчетные сетки являются многоблочными структурированными и состоят из гексоидальных (шестигранных) элементов.

При построении сетки были выполнены следующие основные требования:

• отношение сторон гексоида (Aspect Ratio) для каждой ячейки не превышает 150;

• углы скоса сторон гексоида (Skew) выдерживаются в диапазоне от 15 до 165°;

• количество ячеек поперек пограничного слоя в О-сетке — от 10 до 15;

• количество ячеек в областях закругления на носке и хвостике лопатки — не менее 15 в каждой индексной плоскости (I, J);

• плавность изменения размеров ячеек сетки на границах блоков;

• количество ячеек вдоль лопатки — не менее 120 для рабочего колеса и не менее 100 для направляющего аппарата;

• сгущение сетки вдоль лопатки к втулке (в большей степени) и к корпусу;

• общее количество ячеек — не менее 900 тыс. для лопатки рабочего колеса и не менее 400 тыс. для лопатки направляющего аппарата.

Как показывает практика, расчетные сетки с указанными параметрами позволяют получить приемлемое для определения интегральных характеристик поле течения.

Построение модели численного исследования

Физическая и расчетная модели строились на основе представлений о физических процессах и газодинамическом режиме течения. Расчетная модель CFX включает соотношения для параметров среды (воздуха), уравнения движения полностью сжимаемого газа (осредненные уравнения Навье — Стокса), модели турбулентности (k-, k-, SST) с пристеночными функциями. Для области расчета, включающей лопатку рабочего колеса, определялось вращение с заданной частотой. В законы сохранения при этом вводятся дополнительные члены для сил, возникающих в неинерциальной системе координат.

Для создания расчетной области использовалась импортированная из CFX TurboGrid расчетная сетка для каждого венца. Граничные условия определялись на всех поверхностях и включали условия на твердых стенках, условия на входе и на выходе ступени, периодические интерфейсы для каждого венца и интерфейсы между вращающимися и неподвижными областями.

Граничные условия на твердых стенках (поверхности лопаток, втулки, корпуса) были определены как условия прилипания на гладкой адиабатической стенке.

Граничные условия на входе ступени задавались с фиксацией полного давления (101 325 Па), полной температуры (288,15 К), параметров турбулентности (степень турбулентности 0,02, масштаб турбулентных вихрей 0,003 м).

Граничные условия на выходе ступени (область НА1) задавались либо с экстраполяцией всех параметров потока («свободный выход»), либо с фиксацией среднего по площади выхода статического давления, превышающего значение, полученное на режиме с экстраполяцией. Верхняя граница среднего статического давления на выходе определялась исходя из поведения кривой «расход — степень повышения полного давления» и устойчивости численного расчета.

На периодических границах областей определялись условия периодического интерфейса между боковыми сторонами расчетной области для каждого венца.

На сопрягающихся границах областей, которые принадлежат к разным венцам, определялся интерфейс между вращающейся и неподвижной областью (Stage), который производит интерполяцию между сопрягающимися расчетными сетками с учетом изменения системы координат и выполнения законов сохранения.

Начальные условия определялись с учетом режима течения, оценок осевой скорости течения газа (~100 м/с) и статического давления в потоке. Корректно выбранные начальные условия позволяют ускорить сходимость процесса расчета и получить физически состоятельное решение.

Параметры численного метода выбирались исходя из требований к точности моделирования конвективных и диффузионных процессов, а также разрешения пространственных и временных масштабов течения. Использовался численный метод второго порядка точности по пространственным переменным для всех уравнений системы законов сохранения. Интегрирование по времени в CFX велось по неявной схеме, что позволяет вести устойчивый быстросходящийся расчет. Величина шага по времени выбиралась с учетом максимальных скоростей газа и характерных размеров областей течения (зоны в окрестности периферии, отрывные зоны, окрестности скачков уплотнения, следы) и составила на практике 1x10^-5 ...3x10^-5с.

Критерием сходимости является достижение величиной среднеквадратичной невязки уровня 10^-4 или ниже в совокупности с установлением интегральных характеристик, что достигается приблизительно за 500 шагов по времени и соответствует прохождению потоком ~10 продольных размеров ступени.

Учет трехмерной деформации лопатки под действием центробежных и газодинамических сил

Из-за высокой угловой скорости вращения рабочего колеса возникает вопрос о влиянии центробежных сил и других факторов на форму лопатки рабочего колеса, а следовательно, на течение в компрессоре и характеристики его работы. Для определения степени влияния различных факторов необходимо рассмотреть сопряженную задачу. Проанализируем влияние различных факторов на деформацию лопатки.

Статическое давление. Для расчета влияния газодинамических сил сначала было получено поле распределения статического давления на поверхности лопатки рабочего колеса для недеформированной лопатки. Расчет поля течения проводился в СFX-5. Далее была построена конечно-элементная модель лопатки рабочего колеса в пре/постпроцессоре FEMAP. В качестве поля поверхностных нагрузок в нее было добавлено поле статического давления из файла, экспортированного из CFX-5. Проведенный расчет напряженно-деформированного состояния с учетом только газодинамических сил дал максимальное смещение поверхности в 6x10^-4мм, что, очевидно, не может оказывать существенного влияния на газодинамические процессы в компрессоре.

Температурные напряжения. Максимальная и минимальная температура на лопатке РК1 по результатам вычислений в пакете CFX-5 колеблется от 290 до 360 K. Такой разброс температур не оказывает существенного влияния на свойства материала, из которого сделана лопатка (сплав ВТ-3), а также на тепловую деформацию лопатки.

Обратное влияние газодинамического нагрева лопатки на течение в ступени может быть учтено путем модификации граничных условий в CFX-5 (вместо отсутствия теплообмена может быть поставлено условие со средней температурой поверхности), а в более полной постановке может быть решена задача сопряженного теплообмена.

Центробежные силы. Расчет деформации лопатки с учетом только центробежных сил проводился с помощью программного пакета ABAQUS двумя способами: в рамках линейной постановки и в рамках нелинейной постановки. Расчет в рамках линейной теории дал максимальную деформацию 3,6 мм, в рамках нелинейной теории максимальная деформация составила 2,06 мм.

Величина деформации лопатки оказывается сравнимой с толщиной лопатки, при этом нелинейные эффекты играют большую роль при таких центробежных нагрузках, поэтому следует считать более правильным решение в нелинейной постановке.

Для газодинамических расчетов была выбрана новая форма лопатки, полученная в нелинейной постановке в пакете ABAQUS.

После расчета нелинейных деформаций на основе координат профилей в сечениях недеформированной лопатки РК1 и соответствующих этим точкам смещений была построена новая геометрическая модель на базе модифицированных сечений.

На рис. 2 показан периферийный профиль лопатки в исходном положении и в положении после учета деформации под действием центробежных сил, рассчитанной по программе ABAQUS.

Для изучаемого компрессора при рассмотрении деформации пера лопатки определяющими являются центробежные силы. Это обусловлено тем, что компрессор является модельным, причем линейная скорость соответствует натурной скорости, поэтому частота вращения рабочего колеса является высокой. В натурных объектах угловая скорость вращения меньше, но размеры и площадь лопатки больше, вследствие чего газодинамические силы могут быть существенными и их следует учитывать при расчете формы лопатки.

Результаты расчетов и сравнение с экспериментом

На рис. 3 приведена схема проточной части первой ступени компрессора с указанием сечения, где устанавливались датчики в эксперименте, и места экспорта данных с граничных поверхностей из CFX.

С целью выяснения влияния на газодинамические характеристики компрессора деформации лопатки, вызванной действием центробежных сил, была проведена серия расчетов с учетом деформации лопатки по различным теориям.

Рассматривался режим, который близок к линии рабочих режимов компрессора. Степень повышения полного давления для этого режима в расчете составляет  = 1,839 при расходе G_{в пр}  = 18,76 кг/с, в эксперименте  = 1,861, G_{в пр}  = 18,9 кг/с.

На рис. 4 приведены осредненные распределения степени повышения полного давления за РК1 и НА1 в сравнении с экспериментальными данными. Разница между режимами ( = 1,839 и  = 1,861) составляет 0,022 (1,2%).

На рис. 5 представлены осредненные распределения полной температуры для расчета, которые хорошо согласуются с экспериментом. Расчетный и экспериментальный интегральный КПД ступени составляют 77,5 и 80,1% соответственно.

Рассмотрим интегральные характеристики для исследуемых режимов. Сравнение результатов расчета для исследуемых режимов и различных способов учета деформации лопатки приведено на рис. 6.

С точки зрения определения рабочих режимов важно рассмотреть совмещенные данные по степени повышения полного давления и интегральному адиабатическому КПД. На рис. 7 представлены зависимости степени повышения полного давления от расхода и интегрального адиабатического КПД. На этом рисунке можно определить степень повышения полного давления и расход для режима с максимальным КПД.

Следует отметить существенное улучшение согласования расчетных и экспериментальных данных для геометрии, рассчитанной с учетом нелинейных эффектов в программе ABAQUS.

Несмотря на расхождение в некоторых деталях течения, интегральные характеристики показывают достаточно хорошее соответствие между расчетными и экспериментальными данными, особенно для геометрии, скорректированной с учетом центробежных сил. Это говорит о важности учета эффектов изменения геометрии.

Выводы и рекомендации

1. Проведенные расчеты первой ступени двухступенчатого модельного компрессора с учетом раскрутки пера лопатки соотносятся с результатами эксперимента следующим образом:

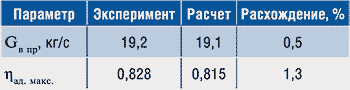
Сравнение распределений основных параметров по высоте канала в расчете и эксперименте показало их удовлетворительное совпадение. В районе втулочной зоны расчет показал параметры выше экспериментальных для степени повышения полного давления и адиабатического КПД и ниже для полной температуры. В связи с этим следует отметить, что расчетная область для ВНА не включала полностью кок компрессора, что, вследствие нарастания пограничного слоя на нем, могло дать потери в районе втулки, наблюдаемые в эксперименте.

2. Удовлетворительное совпадение расчетного и экспериментального распределения параметров по высоте канала характеризует модель турбулентности SST как адекватно описывающую процессы турбулентного переноса для течения в компрессоре. Пристеночные граничные функции позволяют снизить объем расчетной сетки в районе твердых стенок.

3. Учет центробежных и газодинамических сил с помощью прочностного пакета ABAQUS показал, что условный центр вращения профиля лопатки находится в хвостовой части профиля лопатки, и это позволило существенно уточнить параметры расчета и приблизить их к результатам эксперимента. Для получения хороших результатов в пакете CFX при проведении расчетов следует использовать геометрические данные, максимально приближенные к той геометрии, которую будет иметь перо лопатки в рабочем состоянии на соответствующем режиме.

4. Средства CFX позволяют проводить расчет в системах распределенных вычислений разной архитектуры. При проведении расчета в системе распределенных вычислений МВС-1000/16 было достигнуто ускорение расчета до 12 раз по сравнению с расчетом на компьютере с одним процессором.

5. Наибольшие потери полного давления в течении имеют место на периферии рабочего колеса, где присутствует почти прямой скачок уплотнения. В связи с этим рекомендуем модифицировать лопатку РК1 на периферии так, чтобы скачок уплотнения составлял меньший угол с линиями тока.

6. Дальнейшее улучшение точности расчета может быть достигнуто при дополнительном учете следующих факторов: увеличение объема расчетной сетки и качества интерфейсов с целью лучшего разрешения деталей течения в пограничных слоях и отрывных зонах, учет зависимости параметров воздуха от температуры, учет влияния радиального зазора на течение на периферии, учет влияния нагрева лопатки на течение, исследование влияния поворота лопаток НА1.

«САПР и графика» 4'2005