Решение системы линейных алгебраических уравнений в параметрическом моделировании
Система КОМПАС 3D предназначена для создания моделей (деталей и сборок) и графических документов. Параметрическое моделирование — неотъемлемая часть КОМПАС 3D (как и всех современных CAD/CAM-систем), позволяющая быстро получать модели типовых изделий на основе прототипа.
Особенностью системы КОМПАС 3D является использование собственного математического ядра и параметрических технологий.
В этой статье рассматривается построение параметрического двумерного эскиза или чертежа. При этом параметрическая модель состоит из развитого набора геометрических и алгебраических ограничений, заданных на конечном множестве геометрических объектов и переменных. Наиболее распространены такие объекты, как точки, отрезки, окружности и дуги окружностей. А параметрические зависимости описываются с помощью таких геометрических ограничений, как параллельность, перпендикулярность, совпадение, касание, линейные и угловые размеры и прочие отношения. Задачей параметризации в таком случае является решение, благодаря которому все геометрические объекты эскиза (чертежа) приводятся в состояние, удовлетворяющее заданным ограничениям.
На рис. 1 представлен пример параметрического эскиза.
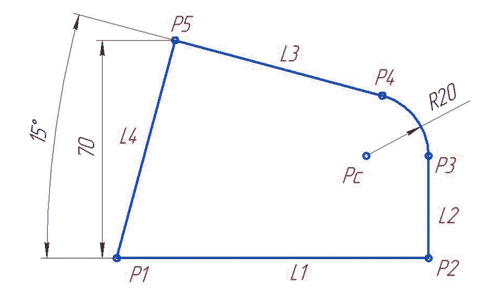
Рис. 1. Пример недоопределенной параметрической модели
Изображение на этом рисунке состоит из четырех прямых, шести точек, одной переменной и описывается системой из 20 ограничений:

где dispp (P1, P2, V) — расстояние на величину V между точками P1 и P2, displ (P, L, V ) — расстояние от точки P до прямой L, fix (P, c) фиксация координаты c у точки P, ang (L1, L2, V) — угол V между прямыми L1, L2, fix (V,const) — присвоение переменной V=const, hor (L) — горизонтальность прямой.
Каждое из ограничений убирает одну степень свободы объекта. С учетом того, что степень свободы точки и прямой равна 2, а переменной — равна 1, вся модель описывается 4*2 + 6*2 + 1 = 21 координатой степеней свобод. Таким образом, недостает ровно одного ограничения, чтобы полностью зафиксировать все объекты модели. Например, точки P2, P3, P4, Pc и прямая L2 имеют одну степень свободы перемещения, и в целом модель недоопределена.
Существуют различные подходы и методы решения задачи параметризации, и все они в основном подразделяются на методы, основанные на графах, на алгебраические и на численные:
• методы, основанные на графах, используют отвлеченную от геометрии эскиза информацию о структуре системы ограничений, например, для разбиения сложной в целом модели на более простые сепаратно решаемые подсистемы;
• алгебраические методы применяют к подсистемам, которые могут быть решены в аналитическом виде;
• численные методы хотя и проигрывают алгебраическим в эффективности, применяются в том случае, если ни один из альтернативных подходов не позволяет решить общую задачу.
Программное средство в составе CAD-системы, которое обеспечивает решение задач параметризации, как правило, применяет все описанные подходы в совокупности.
Для получения численного решения используют итерационные методы, которые, как известно, предполагают некоторое начальное приближение решения системы нелинейных уравнений. Оно уточняется на каждом шаге (итерации), пока не будет достигнута требуемая точность. Широко известный метод Ньютона-Рафсона на каждой итерации отыскивает решение системы линейных алгебраических уравнений (СЛАУ) согласно его итерационной формуле:
![]() (1)
(1)
где k — номер итерации, pk — вектор решения на k-й итерации, Dp — вектор направления поиска решения, F — вектор значений функций, составляющих правую часть системы нелинейных уравнений, J — матрица Якоби ![]() , состоящая из частных производных 1-го порядка.
, состоящая из частных производных 1-го порядка.
Для привлечения метода Ньютона к решению параметрической модели последняя формулируется в виде системы нелинейных алгебраических уравнений F(p) = 0 из функций в (1) .
Особенность параметрического моделирования состоит в том, что в общем случае система уравнений недоопределена, то есть количество неизвестных превышает количество уравнений. Кроме того, матрица J на некоторой итерации, в том числе и при начальном приближении, может оказаться вырожденной или близкой к таковой, что создает дополнительные трудности применения метода Ньютона.
Согласно (1), на каждом шаге итерационного процесса мы сталкиваемся с решением СЛАУ
![]() (2)
(2)
где A ![]() Rm,n, m — количество строк матрицы (количество уравнений), n — количество неизвестных, вектор правых частей c
Rm,n, m — количество строк матрицы (количество уравнений), n — количество неизвестных, вектор правых частей c ![]() Rm , вектор неизвестных x
Rm , вектор неизвестных x ![]() R .
R .
Вектор x определяет величину ![]() в (1). В общем случае rank(A) < m < n . Например, при решении системы нелинейных уравнений, получаемой из модели, показанной на рис. 1, при начальном приближении формируется прямоугольная матрица A
в (1). В общем случае rank(A) < m < n . Например, при решении системы нелинейных уравнений, получаемой из модели, показанной на рис. 1, при начальном приближении формируется прямоугольная матрица A ![]() R 20,21. Как оказалось, матрица имеет неполный ранг (rank(A)=18) по причине того, что в СЛАУ присутствуют два уравнения, векторы-строки которых образуют линейную комбинацию с другими уравнениями. В итоге СЛАУ в этом примере имеет бесчисленное множество решений, удовлетворяющих условию минимума
R 20,21. Как оказалось, матрица имеет неполный ранг (rank(A)=18) по причине того, что в СЛАУ присутствуют два уравнения, векторы-строки которых образуют линейную комбинацию с другими уравнениями. В итоге СЛАУ в этом примере имеет бесчисленное множество решений, удовлетворяющих условию минимума
![]()
Для обеспечения сходимости процесса (1) в этом множестве выбирают вектор минимальной длины (нормальное решение). Известные алгоритмы решения недоопределенных СЛАУ [1, 2] не учитывают разреженную структуру больших матриц и, как следствие, обладают малой скоростью.
Р.М.Ганеев для повышения скорости решения предложил строить нормальное решение на базе предварительного приведения СЛАУ к треугольной форме.
Пусть ранг матрицы СЛАУ (2) меньше количества неизвестных. Для приведения СЛАУ (2) к треугольной форме используются методы отражений Хаусхолдера или отражений/вращений Гивенса. В случае СЛАУ с разреженной матрицей более эффективны методы Гивенса.
Пусть после приведения к треугольной форме получена совместная СЛАУ:
Rx = b (3)
где R — правая треугольная n*n -матрица. При этом считаем, что i -е уравнение отсутствует, то есть в матрице R в i-й строке находятся только нули, и в векторе правой части i-й элемент равен нулю. Таких уравнений может быть несколько.
Коэффициенты дополнительного i -го уравнения вычисляются по формулам:
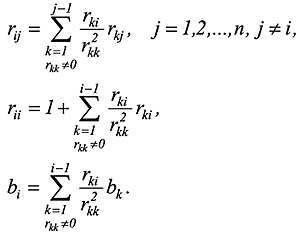 (4)
(4)
Общий алгоритм решения СЛАУ (2) содержит следующие шаги:
1. Параметры СЛАУ (2) необходимо записать в расширенную матрицу: R = [ A Ю ].
Матрица R должна содержать не менее n строк. Если количество уравнений m меньше количества неизвестных (m < n) , то ниже массивов СЛАУ (2) нужно добавить (n-m) строк с нулями:
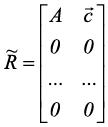
2. Преобразовать матрицу R к правой треугольной форме.
3. Попробовать решить СЛАУ:
3.1. Если R(n,n) = 0 , то произвести переход в 3.2.
3.1.1. Вычислить n-ю компоненту вектора решения:
x(n) = R(n,n+1) / R(n,n)
3.1.2. Пересчитать правую часть с учетом вычисленного компонента вектора решения и перенести на место n-го столбца:
R(k,n) = R(k,n+1) – R(k,n)*x(n), k = 1,2,...,n–1.
3.1.3. Уменьшить счетчик количества неизвестных: n = n–1 .
3.1.4. Если n = 0 , то произвести переход в пункт 4.
3.1.5. Произвести переход в 3.1.
3.2. Построить недостающие уравнения. Возможны два варианта.
3.2.1. В R обязательно есть хотя бы одна строка, в которой элемент rii равен нулю, а остальные элементы этой строки не все равны нулю. Обнаружив такую строку с номером i (i = 1,2,3...) , нужно переместить ее в первую же свободную строку ниже (хотя бы одна свободная строка, благодаря пункту 3.1, обязательно есть) и на месте i-й строки построить дополнительное уравнение. Произвести переход в пункт 2.
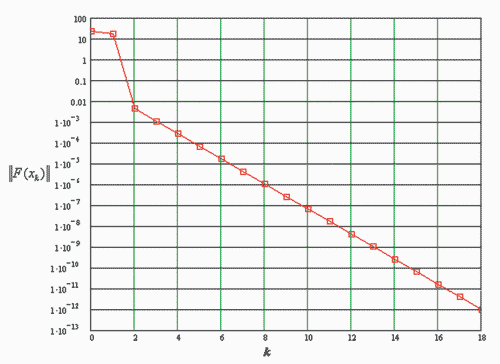
Рис. 2. График сходимости итерационного процесса на примере модели из параметрического эскиза (рис. 1)
3.2.2. В R нулевые диагональные элементы расположены только в свободных строках. В этом случае построить все недостающие уравнения. Произвести переход в пункт 2.
4. Конец вычислений.
Выводы и результаты
Для испытания предложенного метода был поставлен ряд вычислительных экспериментов с решением различных параметрических моделей. График на рис. 2 показывает сходимость итерационного процесса на примере модели, показанной на рис. 1. Характеристика снята в виде зависимости невязки || F(xk) || на каждом шаге решения от номера итерации k . В этом примере отрабатывалось решение системы уравнений для изменения угла между L1 и L3 с 15° на 45°.
Из графика видно, что процесс решения по предлагаемому методу имеет устойчивую сходимость.


