О «достоверности» расчетов конструкций методом конечных элементов

Дмитрий Назаров

В последнее десятилетие в программах конечноэлементного анализа проектируется значительное количество конструкций (самолеты, корабли, ракеты, мосты, ангары, автомобили…). Используются эти конструкции не только проектировщиками. Справедливо желание журнала «САПР и графика» помочь читателям понять реальные возможности метода конечных элементов (см. «САПР и графика» №2-5’2000) и, вероятно, занять активную позицию «за» или «против», учитывая, что речь идет об ошибках не на 5-10%, а на 100% и более (то есть об ошибках принципиальных).

Свободный международный рынок при наличии высоких прибылей готов узаконить и начать активно продвигать любое научное заблуждение. Зачастую примитивные технические усовершенствования преподносятся как величайшее достижение человечества. Иногда абсурдность «достижений» настолько очевидна, что даже при суперрекламе продвижение товара, навязываемого потребителю, оказывается затруднено. Иногда наоборот, наличие суперрекламы, несмотря на очевидность обмана, оказывается более эффективным, чем здравый смысл. И хотя все это уже знакомо нам с раннего детства (см. «Голый король», Г.-Х.Андерсена) однако каждый из нас оказавшись под влиянием рекламы, нередко принимал неверные решения.

Мифы о достоверности расчетов программ конечноэлементного анализа невольно заставляют задуматься о необходимости академий, университетов, НИИ и т.д.: ведь уровень знаний, необходимых для отрисовки модели, ничтожно мал, а красивые разноцветные картинки, представляющие результаты расчетов, выглядят настолько впечатляюще! Однако не стоит забывать, что основной проверкой любого из результатов расчетов был и остается физический эксперимент. Необходимо помнить, что любой из расчетов представляет всего лишь моделирование реальной конструкции, и от того, насколько удачны модель и математический аппарат, реализующий эту модель, зависит соответствие (или несоответствие) результатам экспериментальной проверки. Десятилетиями ученые создавали рекомендации для проектировщиков, четко указывая на рамки применимости той или иной расчетной формулы, прежде всего на основе физических экспериментов. Однако реалии жизни заставляют проектировщиков и конструкторов принимать решения, не описанные в рамках норм для проектирования. Иногда им помогает возможность проведения физического эксперимента на модели, а иногда используются «достоверные» конечноэлементные программы. «Достоверность» метода конечных элементов нам и предстоит выяснить, приведя анализ возможностей, а также используя мнения оппонентов.

Отметим, что научные заблуждения свойственны любому человеку, это нормальное (именно нормальное) развитие процесса познания. Однако если ранее достижения или просчеты ученых не оказывали грандиозного влияния на человечество в целом, то сегодня это стало достаточно опасным. Про судьбы отдельных ученых мы здесь не говорим, это тоже жесткое, но нормальное развитие процесса познания. Но если с точки зрения опасности для человечества представление о Земле (планета, центр Вселенной, тарелка и пр.) не является катастрофичным, то другие заблуждения ученых могут дорого обойтись человечеству.

До практического использования реакции ядерного распада физики-ядерщики просто не знали о вреде радиации. Однако первое массовое применение достижений ядерной физики (Хиросима и Нагасаки) четко показало, насколько губительно воздействие радиации. Начни физики с ядерных электростанций, человечество долго еще не узнало бы о вреде радиоактивного излучения. Изобретение химиков начала века — мощнейший яд ДДТ — также достаточно долго считался абсолютно безопасным. О вреде инертного газа фреона длительное время никто и не думал (ведь газ инертный), однако сегодня почти всем известно о расширяющейся «озоновой дыре» над Австралией и общемировом моратории на применение этого газа.

Перефразировав крылатую фразу, напомним, что эксперимент — он и в Африке эксперимент. Легко проверить, насколько случайно полученное оппонентами решение только первой (см. «Об использовании метода конечных элементов при решении геометрически нелинейных задач» в «САПР и графика» № 4’2000) из четырех тестовых задач (см. «Обзор современных программ конечноэлементного анализа» в «САПР и графика» № 2’2000), например, малым изменением жесткости (к примеру, правого элемента до 2300) или дублированием в одном файле первой задачи, но для одной конструкции указав силу 10, а для другой — 95. Предположим, что в решении, представляющем анализ простейшей конструкции с двумя степенями свободы, ошибок нет. Также предположим, что и в теории МКЭ нет ошибок, а правильный результат получен с первого раза (а не из серии проб для настроек).

Наша задача с рангом матрицы 2 решалась 13 секунд (как указали оппоненты). Определим, сколько времени потребуется на решение системы с рангом матрицы 300:

2^x=13 => x~3,6 => 300^3,6=827 249 506 с, или около 26 лет.

Таким образом, в случае конечноэлементного анализа системы, к примеру, из 100 узлов с тремя степенями свободы на поиск правильного решения программа затратит время, значительно превосходящее разумное. Стоимость такого расчета значительно превысит стоимость постановки физического эксперимента. Об актуальности результатов расчета через четверть века и говорить не приходится. Инженеры, использующие МКЭ, знают, что реальную задачу сотней узлов не опишешь: обычно требуется несколько тысяч узлов. Интересно, что они получают за полтора-два часа расчетов? Отметим, что рассуждения о продолжительности расчетов касаются существующих программ МКЭ, которые по своей сущности не способны получить правильного результата в нелинейных задачах. Проблема оказывается еще более острой с учетом того, что определить «на глазок» или с помощью МКЭ, является задача линейной или нелинейной, невозможно. А учитывая возможность большого количества возможных «правильных» решений с точки зрения статического равновесия, которое может быть определено как 2^{кол.узлов}, даже вероятностный поиск решения нереален. Например, взяв все те же 100 узлов, имеем 1 267 650 600 228 229 401 496 703 205 376 возможных состояний правильного статического равновесия. Как называется число разрядности 1030, затруднительно ответить, однако легко сообразить, что поиск правильного результата среди этого множества «правильных» решений нереален (для сравнения — протяженность Вселенной оценивается астрономами в 10²⁹ мм).

По мнению оппонентов (в их высоком профессионализме сомневаться не приходится), рассмотревших только первую из четырех тестовых задач, «аналитическое решение поставленной задачи не представляется возможным». Добавим: да, оно невозможно, но только в рамках классического конечно-элементного моделирования, который оппоненты применили для анализа (то есть вручную повторили программный расчет). Однако рассмотрев возможное поведение конструкции (рис. 1), не так уж сложно привести аналитические решение.

Опуская промежуточные выкладки, приведем то самое «невозможное» аналитическое решение первой (из четырех) представленных тестовых задач (обозначения см. на рис. 1). Напомним, что каждая из задач являлась тестом разных ошибок, заложенных в метод конечных элементов. Отсутствие решений остальных задач уже о чем-то свидетельствует. Хотя, вероятно, занятость нескольких тысяч как отечественных, так и зарубежных «экспертов» и ученых (без кавычек), которым тестовые задачи стали известны, не позволила им потратить еще по 13 секунд на каждую из задач, однако не помешала сотням из них писать многостраничные опусы в адрес автора задач.

Итак, то самое «невозможное» решение:

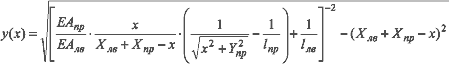(1),

где x — горизонтальная проекция правого элемента, а y(x) — вертикальная проекция левого элемента,

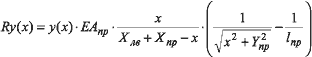(2),

где Ry(x) — вертикальная реакция левого элемента (вертикальная проекция усилия в правом элементе).

Несложно убедиться, что все решение фактически зависит от одного параметра — горизонтальной проекции правого элемента (x).

Откладывая по оси абцисс y(x), а по оси ординат Ry(x), строим график зависимости Ry от Dy = (y–Y_лв) (рис. 2), для удобства анализа совместив с внешней силой (P).

Интересный момент: статическая сторона задачи полностью описывается одним параметром (x), а не двумя, как в МКЭ.

На графике росту приложенной силы (P) соответствует кривая A-B-E-F-H-I (черная пунктирная линия). Напомним, что нами рассматривается статическая внешняя сила, а она (по определению) растет от нуля до указанной расчетной величины. Таким образом, внешняя сила, достигнув значения P_b, не уменьшается (если в бак накапало 95 литров, то меньше уже не станет). Реакция левого элемента (Ry), в зависимости от перемещения узла (Dy), представлена кривой A-B-C-D-E-F-G-H-I (красная сплошная линия). Подобное нелинейное поведение давно используется в быту (например, в выключателях, не допускающих искрового проскока). Очевидно, что на кривой C-K-D и F-L-G (желтый штрих-пунктир), конструкция оказаться не может, хотя бы по причине невозможности (после достижения внешней силой значения P_b) перемещения узла в обратном направлении (создавая отрицательную работу). Вспомним про бак: 95 литров воды ну никак не превратятся в «анти-95» литров. Учитывая, что и великим ученым свойственно заблуждаться, простим этот недосмотр оппонентам в надежде на то, что интерес к научной проблеме у них окажется выше.

Несложно догадаться, что раз на участке B-E отсутствует статическое равновесие, то необходимо учитывать динамические составляющие, которые в используемом методе конечных элементов как раз отсутствуют. В силу того, что приведенная модель является простейшей моделью нелинейной конструкции, мы вправе сделать вывод о невозможности корректного расчета нелинейных моделей программами конечноэлементного анализа. Безусловно, сторонники «за» могут возражать, утверждая, что можно использовать «динамический конечноэлементный анализ», но мы попросим их не спешить с выводами, а предложим все же проанализировать конструкцию. Напомним, что задание внешней нагрузки как параметра от времени еще не значит, что вам удастся решить поставленную задачу. Динамический анализ нелинейных конструкций очень интересен. К примеру, самый первый (бросающийся в глаза) вывод, что в нелинейных задачах время «отдыхает». Как это ни странно, без использования параметра времени удается определить все составляющие движения (ускорение, скорость, перемещение…). Все, за исключением одного параметра — времени.

В силу этих замечаний можно обоснованно поставить под сомнение корректность анализа подобных систем и более продвинутыми пакетами (LS/Dyne, ADAMS, DADS, Accupak). При желании читателей автор сделает обзор (с указанием freeware и GPL) и этих пакетов, используемых в основном для анализа гидроаэродинамических, акустических и подобных задач.

Разумеется, актуальные для человечества проблемы нелинейности требуют научного обсуждения, так как результаты конечноэлементного анализ напрямую используются для изготовления ракет, самолетов, кораблей, автомобилей, мостов, ангаров и т.д. Причем используются они без экспериментальной проверки (как в случае, например, с Boeing-747), что ведет к неминуемым катастрофам. Катастрофы, причинами которых сегодня считаются прогоревшие прокладки, незакрученные болты, плохие фильтры и т.д., возникают по причине проверки расчетов все на тех же программах, которые принципиально не дают правильного результата.

Хочется надеяться, что на основе изложенного материала читатели смогут прийти к собственному (а не продиктованному рекламой) решению: на сегодняшний момент можно однозначно заявить, что метод конечных элементов неприменим для решения нелинейных задач.

«САПР и графика» 7'2000