Анализ прочности промышленных трубопроводов в ANSYS и ABAQUS

Владимир Алешин, Вячеслав Кобяков, Вадим Селезнев

Автоматизированный анализ прочности трубопроводов в ANSYS

Программирование на APDL в ANSYS

Анализ прочности трубопроводов в ABAQUS

Эффективность применения современных средств компьютерного моделирования на стадиях разработки, проектирования и изготовления сложных технических систем, в частности промышленных конструкций, уже ни у кого не вызывает сомнения. Различные системы автоматизированного проектирования CAD/CAE сейчас широко используются в научно-исследовательских, проектных и производственных организациях практически всех отраслей отечественной промышленности, о чем свидетельствуют публикуемые в журнале «САПР и графика» материалы.

Однако после изготовления конструкции начинается процесс ее многолетней эксплуатации. Обеспечение безопасной эксплуатации промышленной конструкции, даже построенной по технически безупречному проекту (выполненному с использованием новейших средств компьютерного моделирования), невозможно без ее периодического освидетельствования, технической диагностики, оценки фактического состояния и своевременного ремонта и замены изношенных деталей. К сожалению, во многих случаях анализ фактического состояния эксплуатирующихся промышленных конструкций по результатам технической диагностики проводится не только без применения средств компьютерного моделирования, но и вообще без каких-либо надлежащих расчетных оценок. Для этого используются разработанные десятки лет назад на основании результатов модельных экспериментов и многократно, но без существенных изменений переписанные в нормативных руководствах таблицы, в лучшем случае простейшие полуэмпирические формулы, для определения допустимости тех или иных видов дефектов.

Интересно отметить, что такой разрыв в подходах к проектированию новых и оценке технического состояния действующих промышленных объектов, например в наиболее знакомой авторам нефтегазовой отрасли, характерен для всех индустриально развитых стран мира. Не снижающееся количество аварий на различных промышленных предприятиях свидетельствует, что и в других отраслях положение не лучше.

Необходимость скорейшего изменения такой ситуации очевидна, особенно на эксплуатирующихся десятки лет объектах опасных производств российской промышленности, оборудование которых находится на грани, а иногда и за гранью исчерпания своего проектного ресурса.

Одним из примеров таких объектов являются промышленные трубопроводные системы высокого давления, транспортирующие опасные жидкости и газы на предприятиях нефтегазовой, химической и энергетической отраслей промышленности.

В конце ХХ века в Центре вычислительных технологий механики ООО «НПО ВНИИЭФ-ВОЛГОГАЗ» (ЦВТМ) была разработана вычислительная технология комплексного анализа состояния трубопроводов PipEst, предназначенная для выявления аварийно опасных участков промышленных трубопроводных систем и их ранжирования по срокам ремонта или замены («САПР и графика» № 7’1999). Основной целью разработки данной технологии являлось внедрение современных методов и средств численного моделирования в повседневную практику специалистов, отвечающих за техническое состояние и безопасность эксплуатации трубопроводных систем.

Одной из наиболее важных областей практического применения технологии PipEst является численный анализ методом конечных элементов (МКЭ) сложного нелинейного напряженно-деформированного состояния (НДС) и оценка прочности промышленных трубопроводных систем с учетом их многофакторного нагружения и данных технической диагностики. Об эффективности применения разработанной вычислительной технологии свидетельствуют успешные решения многих сложных производственных задач, связанных с анализом прочности промышленных трубопроводных систем различного назначения, в частности подземных участков магистральных газопроводов (МГ), выполненные специалистами ЦВТМ в сотрудничестве со специалистами промышленных предприятий как в России, так и за рубежом.

Опыт решения этих задач наглядно показал, что для широкого внедрения разработанной технологии в производственную практику газотранспортных предприятий необходимы создание и реализация программных процедур, позволяющих максимально автоматизировать построение расчетных моделей трубопроводных систем, задание нагрузок и граничных условий, управление расчетом и обработку результатов численного анализа. Использование данных процедур, с одной стороны, существенно снижает время, необходимое для анализа конкретного участка трубопровода, исключив при этом возможные ошибки пользователя; а с другой — дает возможность специалистам, связанным с эксплуатацией и техническим контролем состояния и безопасности газопроводных систем и не имеющим достаточного опыта в области численного моделирования, быстро освоить и эффективно применять данную технологию.

Приступая в 1997 году к производственной эксплуатации вычислительной технологии PipEst в ОАО «ГАЗПРОМ», в качестве средства численного моделирования сложного НДС трубопроводных систем специалисты ЦВТМ выбрали универсальную программу ANSYS. Выбор во многом объяснялся тем, что наряду с другими достоинствами: удобным интерфейсом, широким набором типов конечных элементов, моделей материалов, итерационных «решателей» и т.д., ANSYS в то время была единственной в мире универсальной МКЭ-программой, удостоенной международного сертификата качества ISO9001. Уже тогда в ANSYS имелся достаточно развитой встроенный алгоритмический язык программирования APDL (ANSYS Parametric Design Language), позволяющий автоматизировать отдельные трудоемкие процедуры моделирования. С тех пор в каждой новой версии ANSYS функциональные возможности APDL продолжали интенсивно расширяться, достигнув сегодня (версия 8.1) уровня, позволяющего эффективно автоматизировать практически весь процесс численного прочностного анализа трубопроводных систем.

Таким образом, одно из основных направлений развития вычислительной технологии PipEst в последние годы определялось условиями ее внедрения в производственную практику специалистов предприятий трубопроводного транспорта и соответствующих надзорных организаций и заключалось в разработке программных модулей (макросов) на языке APDL для полной автоматизации процедуры численного прочностного анализа трубопроводов в среде программы ANSYS.

Все модели и алгоритмы блока прочностного анализа технологии PipEst также могут быть реализованы для практического применения с использованием в качестве средства численного моделирования НДС трубопроводных конструкций любой другой универсальной МКЭ-программы нелинейного структурного анализа, обладающей требуемым набором функциональных возможностей или открытой архитектурой для дополнения необходимых модулей. В частности, все наиболее распространенные в мире коммерческие универсальные МКЭ-программы (ABAQUS, LS-DYNA, MSC/NASTRAN, MARC, ALGOR, COSMOS/M и др.) имеют такие возможности и могут быть успешно использованы в качестве «решателей». Следует отметить, что специализированные программы, такие как CEASAR II, TriFlex и т.п., в данном случае не подходят, так как предназначены в основном для проектировочных расчетов и их возможности ограничиваются анализом трубопроводных систем в балочном приближении.

Помимо развития встроенных средств параметрического программирования, эффективность практического использования созданных на базе универсальных МКЭ-программ систем автоматизированного прочностного анализа трубопроводных систем определяется также другими индивидуальными особенностями базовой программы: возможностями и удобством препроцессора; набором реализованных моделей материалов и типов конечных элементов (КЭ); скоростью выполнения нелинейного структурного анализа. Поэтому для максимального повышения эффективности вычислительной технологии PipEst, а также для расширения круга ее потенциальных пользователей в ЦВТМ проводятся работы по адаптации алгоритмов технологии PipEst для других универсальных МКЭ-программ. В настоящее время выполнена реализация процедуры численного анализа сложного нелинейного НДС подземных участков МГ с коррозионными дефектами в среде программы ABAQUS.

Выбор ABAQUS в качестве еще одной базовой программы для реализации технологии PipEst, как и ранее выбор ANSYS, обусловлен объективной ситуацией, сложившейся в настоящее время на рынке коммерческих универсальных МКЭ-программ. Программа ABAQUS (разработка Hibbitt, Karlsson & Sorensen, Inc.) входит в тройку (после ANSYS и MSC/NASTRAN) наиболее продаваемых в мире лицензионных МКЭ-программ. Она превосходит ANSYS по предоставляемым для решения нелинейных задач прочностного анализа конструкций функциональным возможностям, но дешевле программы MSC/NASTRAN, которая после покупки компанией MSC, Inc. модулей программы MARC имеет примерно аналогичные с ABAQUS возможности.

Кроме того, программа ABAQUS является безусловным лидером среди коммерческих МКЭ-программ по распространенности в нефтегазовой отрасли США, Канады и некоторых других западных стран. Так, в США большинство организаций, занимающихся анализом безопасности магистральных трубопроводов, используют для анализа прочности трубопроводных конструкций программу ABAQUS. Такое положение, скорее всего, объясняется изначальной ориентацией разработчиков ABAQUS на нефтегазовою промышленность как на один из наиболее важных секторов продаж программы. Достаточно отметить, что в библиотеке КЭ ABAQUS имеются четыре элемента балочного типа (PSI24, PSI26, PSI34, PSI36), предназначенные для моделирования подземных трубопроводов с учетом их взаимодействия с окружающим грунтом (pipe-soil interaction), чего нет ни в одной из известных нам универсальных МКЭ-программ.

Хотя работы по полной автоматизации процедуры численного моделирования НДС трубопроводных систем в среде программы ABAQUS в настоящее время еще не закончены и активно ведутся в ЦВТМ, уже сейчас можно представить некоторые из полученных результатов, на основании которых можно будет сравнить возможности ANSYS и ABAQUS в области анализа прочности трубопроводных конструкций .

Автоматизированный анализ прочности трубопроводов в ANSYS

Сначала рассмотрим основные особенности автоматизированных процедур прочностного анализа трубопроводных конструкций, реализованных для работы в среде программы ANSYS, на примере моделирования НДС подземного участка МГ. В соответствии с алгоритмами вычислительной технологии PipEst численный анализ сложного нелинейного НДС участка трубопровода выполняется в три последовательных этапа моделирования. На первом этапе протяженный участок трубопровода (как правило, его длина составляет несколько сотен метров) моделируется в балочном приближении. Его конструкция аппроксимируется прямыми и криволинейными КЭ типа PIPE (здесь и далее терминология ANSYS). Нелинейное взаимодействие трубопровода с окружающим его грунтом моделируется с использованием КЭ COMBIN39 («нелинейные пружины»), силовые характеристики которых рассчитываются по полуаналитическим зависимостям сопротивления грунта продольным и поперечным смещениям трубы.

Для использования программного модуля автоматизации построения КЭ-моделей и численного анализа НДС подземного участка трубопровода пользователю необходимо сформировать файл исходных данных. Этот файл представляет собой таблицу заданного формата, содержащую пространственные координаты базовых точек осевой линии трубопровода, характеристики физико-механических свойств материалов (труб и грунтов в зоне прокладки трубопровода), геометрические параметры труб.

Рис. 1. Окно для ввода названия работы

Из главного окна программы ANSYS запускается управляющий командный файл (File>Read Input From…). Пользователь в диалоговом режиме в последовательно появляющихся окнах меню (пример представлен на рис. 1) вводит необходимые для расчета параметры: название работы, имя файла исходных данных, значения действующих нагрузок (внутреннее давление, температурный перепад и т.д.). После ввода параметров программная процедура считывает информацию из файла исходных данных и в автоматизированном режиме производит построение балочной КЭ-модели трубопровода.

Сначала по координатам базовых точек оси трубопровода строится последовательность опорных точек (Keypoints) геометрической модели трубопровода. Затем программная процедура разбивает исследуемый сегмент трубопровода на условно «прямые» (с малой кривизной оси) и криволинейные (отводы) участки. Осевая линия трубопровода строится следующим образом: по группам опорных точек, принадлежащих участкам первого типа, проводятся кубические сплайны, а участки второго типа моделируются в виде дуг окружностей соответствующего радиуса.

Прямые участки аппроксимируются КЭ PIPE16, криволинейные — КЭ PIPE18. КЭ-сетка генерируется исходя из заданной пользователем минимальной длины КЭ. Узлы автоматически перенумеровываются. При этом новая нумерация узлов задается в порядке возрастания номеров по мере увеличения координаты x глобальной системы координат. Затем программная процедура, последовательно рассматривая все узлы, принадлежащие подземному участку трубопровода, создает локальные координатные системы, ориентированные по оси трубопровода. В этих системах координат к каждому узлу добавляется по три узла-копии и создаются три «нелинейные пружины» COMBIN39. Силовые характеристики этих элементов рассчитываются по полученным из файла исходных данных значениям физико-механических свойств соответствующего грунта. На рис. 2 представлен фрагмент балочной КЭ-модели подземного трубопровода с дополнительными элементами COMBIN39, моделирующими взаимодействие труб с окружающим грунтом. Далее программная процедура прикладывает действующие нагрузки и граничные условия и выполняет численный анализ балочной модели подземного трубопровода. Результаты моделирования на первом этапе дают возможность пользователю определить общее НДС всего рассматриваемого трубопровода, выявить наиболее нагруженные участки, выделить их границы и определить на них расчетные значения перемещений и углов поворота.

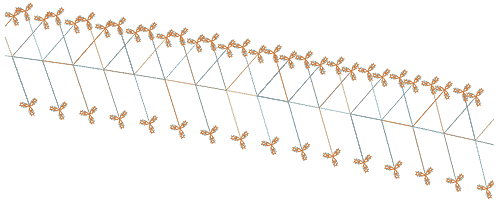
Рис. 2. Балочная КЭ-модель подземного трубопровода (фрагмент)

Выявленные на первом этапе наиболее нагруженные участки трубопровода, а также участки с обнаруженными дефектами стенок (например, коррозионными кавернами) и другие критические участки на втором этапе моделируются с использованием оболочечных КЭ типа SHELL. Грунт, окружающий трубопровод, моделируется объемными КЭ типа SOLID. Нелинейное поведение грунта описывается с использованием реализованной в ANSYS упруго-идеальнопластической модели материала Друкера-Прагера с оптимальной поверхностью текучести (разработанная в ЦВТМ модификация классического критерия Друкера-Прагера). Длина моделируемого на втором этапе участка трубопровода обычно составляет 40-60 м.

Весь процесс подготовки и численного анализа SHELL-моделей подземного участка трубопровода с окружающим его грунтом на втором этапе также выполняется автоматизированно. Для автоматизированной генерации SHELL-модели подземного трубопровода базой служит соответствующая PIPE-модель, созданная на первом этапе моделирования (файл *.db). Также необходим файл результатов (*.rst) PIPE-модели для формирования граничных условий. При запуске в среде ANSYS соответствующего программного модуля пользователю сначала предлагается в диалоговом режиме ввести несколько необходимых параметров: имя файла PIPE-модели, координаты центра выбранного участка, длину моделируемого участка, имя файла SHELL-модели. Все последующие действия по построению и численному анализу SHELL-модели выбранного участка и окружающего его грунта выполняются автоматизированно.

Здесь мы не будем описывать работу разработанных программных модулей на втором и третьем этапах моделирования (подробное изложение всех автоматизированных процедур анализа подземных трубопроводов с примерами APDL-программ можно найти в монографии «Численный анализ прочности подземных трубопроводов» под редакцией В.В.Алешина и В.Е.Селезнева (М.: Едиториал УРСС, 2003), а приведем только некоторые результаты.

Пример геометрической модели подземного участка трубопровода, построенной на втором этапе, приведен на рис. 3. Для наглядности некоторые из частей, моделирующих грунт, на рис. 3 не показаны, разными цветами изображены слои грунта с различными характеристиками физико-механических свойств. В результате расчетов на втором этапе моделирования пользователь получает трехмерную картину распределения напряжений в трубопроводной конструкции с учетом всех действующих на нее эксплуатационных нагрузок (рис. 4).

Рис. 3. SHELL-модель участка трубопровода с окружающим грунтом (фрагмент)

Рис. 4. Распределение эквивалентных напряжений фон Мизеса [Па] на участке подземного трубопровода (SHELL-модель)

На третьем этапе моделирования анализ сложного нелинейного НДС участков трубопровода с дефектами стенок проводится с использованием SOLID-моделей труб. Как и на предыдущих этапах, разработанная программная процедура позволяет автоматизированно выполнить весь процесс генерации необходимых расчетных моделей и численного анализа. Результаты анализа сложного нелинейного НДС участка трубопровода, полученные на третьем этапе моделирования, позволяют оценить его реальную несущую способность с учетом совместного влияния всех действующих факторов: эксплуатационных нагрузок; данных технической диагностики (трехмерная форма дефектов, смещение от проектного положения и т.п.); остаточных упругих напряжений и пластических деформаций в отводах, изготовленных методом холодного гнутья труб; нарушения сплошности засыпки подземных участков, подвергшихся экскавации (образование полостей под трубопроводом). С помощью автоматизированной итерационной процедуры можно также определить расчетное значение разрушающего давления с требуемой точностью (рис. 5).

Рис. 5. Распределение эквивалентных напряжений фон Мизеса [Па] в зоне коррозионных дефектов стенки трубопровода при действии разрушающих нагрузок

Программирование на APDL в ANSYS

Наличие встроенного алгоритмического языка APDL можно выделить как одно из основных достоинств программы ANSYS. Интуитивная ясность и простота и в то же время широкие функциональные возможности делают APDL мощным средством автоматизации всего цикла численного анализа сложных технических систем. Фактически, автоматизация заключается в разработке комплекса макропрограмм, настраивающих ANSYS на решение конкретных производственных задач и позволяющих эффективно использовать современные средства численного анализа специалистам промышленных предприятий, не имеющих опыта работы в среде программы ANSYS и даже не знакомых с численными методами.

В частности, при реализации вычислительной технологии PipEst использование макропрограммирования на APDL на каждом этапе моделирования позволило полностью автоматизировать все процессы генерации КЭ-моделей, приложения граничных условий и нагрузок, численного анализа и обработки результатов. Автоматизированная передача граничных условий была выполнена с использованием процедуры субмоделирования (Submodeling) как для реализованных (от shell-моделей к solid-моделям), так и не реализованных (от pipe-моделей к shell-моделям) в ANSYS случаев.

На трех этапах вычислительной технологии были использованы практически все возможности языка APDL: организация диалоговых и мультидиалоговых окон для ввода текстовых и числовых параметров; создание массивов и ввод значений в массивы из файлов формата ASCII; организация циклов и операторов-условий; передача параметров через базы данных; создание окон статусных строк для отображения работы программы; использование библиотек макроподпрограмм.

Однако наряду с очевидными достоинствами текущая на момент реализации PipEst в среде ANSYS 7.0 версия APDL не была лишена и некоторых недостатков, с которыми специалистам ЦВТМ пришлось столкнуться при разработке макросов. Сейчас мы не будем их перечислять, так как некоторые из них уже исправлены в последующих версиях, а остальные, надеемся, будут исправлены в ближайшем будущем. Предложения по устранению недостатков, а также по дальнейшему развитию APDL были высказаны специалистами ЦВТМ в докладе на международном конгрессе «21 CAD-FEM Users’ Meeting 2003 — International Congress on FEM Technology» (г.Потсдам, Германия), в котором также принимали участие руководители и ведущие специалисты компании ANSYS, Inc.

После введения встроенного алгоритмического языка APDL следующим шагом компании ANSYS, Inc. на пути расширения возможностей автоматизации численного анализа стала реализация (начиная с версии 6.0) макроязыка UIDL (User Interface Design Language), предназначенного для разработки специализированных графических интерфейсов пользователя в среде программы ANSYS. С помощью UIDL команды для вызова APDL-программ, для работы с внешними файлами и управления процессом анализа можно встроить в основное меню программы ANSYS. Это облегчает и делает более удобной работу пользователя со специализированными программными модулями, написанными на APDL. В настоящее время в ЦВТМ ведутся работы по реализации в среде ANSYS графического интерфейса PipEst (рис. 6).

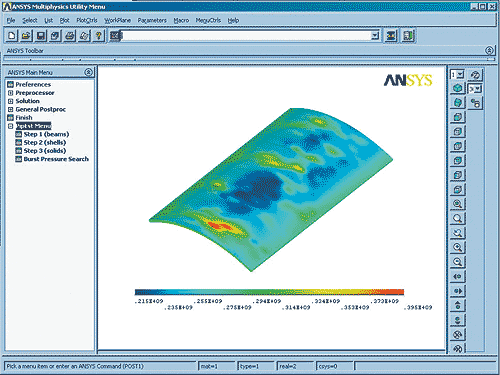
Рис. 6. Командное меню технологии PipEst в среде ANSYS

Анализ прочности трубопроводов в ABAQUS

Для сравнения возможностей ANSYS и ABAQUS рассмотрим решение типичной для газотранспортных предприятий производственной задачи по анализу НДС эксплуатирующегося участка подземного МГ с коррозионными дефектами стенок. Например, возьмем модельный участок трубопровода длиной около 300 м, имеющего изгиб в средней части, схема которого представлена на рис. 7.

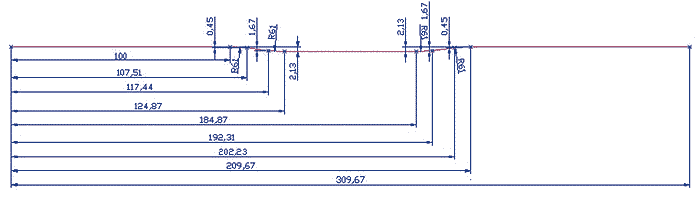
Рис. 7. Модельный участок трубопровода

В качестве исходных данных возьмем обычные для подземных МГ параметры: глубина засыпки — 1 м на всей протяженности участка; тип грунта — суглинок (угол внутреннего трения — 27°, объемный вес — 18,5 кН/м³; удельное сцепление — 22 кПа; модуль деформации грунта — 6 МПа; коэффициент Пуассона — 0,35); наружный диаметр труб — 1,22 м; толщина стенки — 13,5 мм; материал труб — низколегированная сталь (модуль Юнга — 206 ГПа, коэффициент Пуассона — 0,3, предел текучести — 492 МПа, условный предел прочности — 607 МПа, коэффициент линейного теплового расширения — 1,2·10^-5град^-1 ); нагрузки: внутреннее давление — 7,35 МПа, температурный перепад — 40°C. Предположим также, что группа коррозионных дефектов расположена в середине модельного участка трубопровода. Данные по геометрии коррозионных дефектов (матрица остаточных толщин) были взяты из результатов технической диагностики реального участка МГ.

Численный анализ НДС модельного участка трубопровода в ANSYS был выполнен по описанной выше технологии с использованием разработанных макросов. Создать такие же модели в препроцессоре ABAQUS/CAE «вручную» оказалось достаточно трудоемким делом. По крайней мере, намного более трудоемким, чем в препроцессоре ANSYS. Поэтому соответствующие модели для ABAQUS были созданы в виде командных файлов (*.inp) и рассчитывались в ABAQUS в пакетном (batch) режиме.

Здесь следует также отметить, что реализация упоминавшихся выше КЭ типа PSIХХ даже в последней версии программы ABAQUS 6.3 (2003 год) выполнена с достаточно существенными упрощениями, не позволяющими достичь точности моделирования, получаемой с использованием более сложных моделей, разработанных в ЦВТМ и реализованных в технологии PipEst. Поэтому при адаптации PipEst для среды программы ABAQUS все модели и алгоритмы численного анализ сложного НДС подземных участков трубопроводов, реализованные ранее в среде программы ANSYS, на данном этапе оставлены без изменения (КЭ типа PSIХХ для моделирования не использовались).

Подготовка командных файлов для ABAQUS выполнялась в среде ANSYS. При помощи специально написанного макроса производился опрос базы данных ANSYS и последующий вывод полученной информации о КЭ-сетке, моделях материалов, нагрузках и граничных условиях в текстовый файл (*.inp) в пригодном для ABAQUS в формате. Затем этот файл дополнялся другими необходимыми для анализа командами ABAQUS. Таким образом, формировался полностью готовый для расчета «решателем» ABAQUS файл *.inp.

Нельзя не отметить, что численный нелинейный структурный анализ выполняется в ABAQUS заметно быстрее, чем в ANSYS. Например, на решение идентичных задач второго этапа технологии (SHELL-модель трубопровода, solid-модель грунта) ANSYS тратит около двух часов на компьютере Pentium 4 2,4 ГГц, ОЗУ 2 Гбайт, а ABAQUS — около 40 минут на компьютере Pentium III 800 МГц, ОЗУ 500 Мбайт.

После окончания расчета ABAQUS создает файл с запрошенными результатами в текстовом формате и файл для постпроцессора ABAQUS/CAE. Работа ABAQUS/CAE в ОС Windows происходит с использованием специальных программ-эмуляторов Exceed и Exceed 3D (разработка Hummingbird Ltd, Канада). Поэтому, работая с ABAQUS/CAE под Windows, пользователь испытывает некоторые неудобства, связанные с медленной скоростью воспроизведения графических объектов. Следует, однако, заметить, что с самыми большими неудобствами российский пользователь лицензионного ABAQUS под Windows сталкивается при попытке купить нужные версии (не последние!) этих эмуляторов, которые HKS, Inc. вместе с ABAQUS не поставляет. Нам для этого потребовалось около полугода.

Сравнение полученных в ANSYS и ABAQUS результатов показывает, что качественные картины распределения основных характеристик НДС (смещения, углы поворота, тензоры напряжений и деформаций и т.д.) совпадают на всех этапах численного анализа подземных трубопроводов (рис. 8-10). Некоторые количественные характеристики НДС для SHELL- и SOLID-моделей (представляющих наибольший интерес) модельного трубопровода, полученные в ANSYS и ABAQUS, представлены в таблице. Для SHELL-моделей — это поперечные (в вертикальной плоскости) перемещения верхнего и нижнего узлов, принадлежащих срединному сечению трубопровода, и максимальное значение эквивалентных напряжений фон Мизеса в средней части трубопроводного участка. Для SOLID-моделей приведены максимальные значения эквивалентных напряжений фон Мизеса в коррозионной зоне трубопровода, а также компоненты вектора перемещения для узла, в котором возникают максимальные напряжения (здесь наблюдалось максимальное расхождение результатов двух программ). Как видно из таблицы, обе программы дают практически одинаково точные результаты и могут с успехом использоваться для решения практических задач численного анализа прочности подземных трубопроводов.

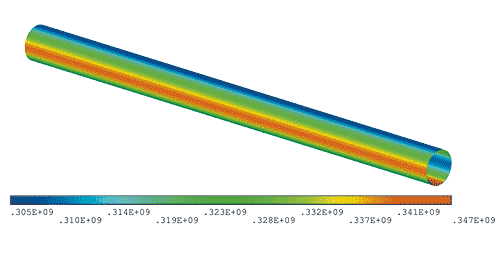
Рис. 8. Эквивалентные напряжения фон Мизеса в средней части трубопровода (SHELL-модель, ANSYS)

Рис. 9. Эквивалентные напряжения фон Мизеса в средней части трубопровода (SHELL-модель, ABAQUS)

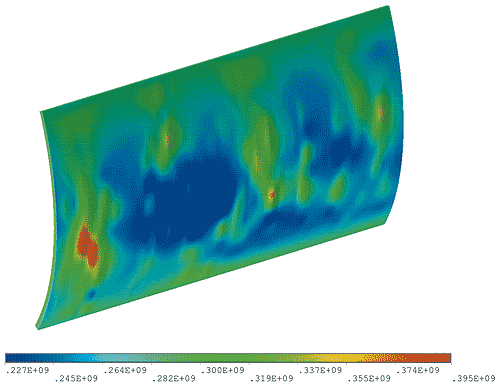
Рис. 10. Эквивалентные напряжения фон Мизеса в коррозионной зоне трубы (SOLID-модель, ANSYS)

В то же время и ANSYS и ABAQUS обладают некоторыми ярко выраженными преимуществами. В ANSYS это более удобный интерфейс пользователя, более широкие возможности препроцессора, а главное — наличие достаточно простого и одновременно мощного средства автоматизации численного анализа — языка APDL.

Основным преимуществом ABAQUS является существенно более высокая скорость выполнения численного нелинейного структурного анализа. К достоинствам этой программы можно отнести также более широкий набор нелинейных моделей материалов. В частности, для моделирования нелинейного НДС окружающих подземный трубопровод грунтов, помимо модели упруго-идеальнопластического материала Друккера-Прагера (реализованной в ANSYS), можно использовать модель материала Друккера-Прагера с упрочнением и несколько модификаций модели упруго-пластического материала Мора-Кулона.

«САПР и графика» 7'2004