Верификация вычислительных алгоритмов системы I-DEAS NX компании UGS PLM Solutions для проведения инженерных расчетов и анализа объектов атомной энергетики

С.Е.Власов, С.А.Пименов, С.А.Перенков

Приложение Simulation системы I-DEAS NX — инструмент для виртуального моделирования и проведения инженерных расчетов

Необходимость верификации вычислительных алгоритмов

Результаты верификации на примере типовых конструкций ПТС

Заключение

Вопросам автоматизации этапов жизненного цикла программно-технических средств автоматизированных систем управления технологическими процессами атомных электростанций (ПТС АСУ ТП АЭС) с применением решений компании UGS PLM Solutions была посвящена публикация в № 11’2004. В настоящей статье приводится технология верификации вычислительных алгоритмов CAE-системы I-DEAS NX для подтверждения точности расчетов конструкций и объектов ПТС, которые являются системами, обеспечивающими безопасное функционирование энергоблока АЭС. Актуальность решения данной задачи имеет две составляющие — необходимость подтвердить достоверность результатов компьютерного моделирования процессов функционирования ПТС в условиях воздействия внешних эксплуатационных факторов, а также необходимость разработать методическое обеспечение для сокращения числа и объема предварительных натурных испытаний конструкций ПТС с принятием результатов виртуального моделирования.

Приложение Simulation системы I-DEAS NX — инструмент для виртуального моделирования и проведения инженерных расчетов

В настоящее время CAE-системы являются инструментом для виртуального моделирования и инженерных расчетов широкого спектра конструкций машин, механизмов, приборов и аппаратуры. Составляющая САЕ в системе I-DEAS NX представлена приложением Simulation.

Приложение Simulation разделено на ряд модулей, каждый из которых предназначен для реализации отдельных этапов инженерных расчетов конструкций, моделирования влияния внешних воздействующих факторов.

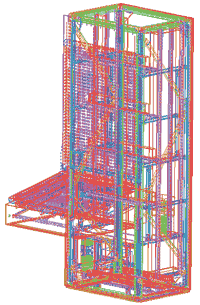
Одной из проблем взаимодействия составляющих CAD/CAE в современных САПР является корректный переход от геометрических моделей, созданных конструкторами, к расчетным моделям, которые используются при инженерном анализе. С точки зрения инженера-расчетчика, геометрические модели конструктора (CAD-модели) имеют избыточность информации и потому не могут быть использованы для корректного наложения дискретных сеток и построения расчетных моделей. Это особенно заметно при создании сложных, подробных моделей конструкций ПТС (рис. 1).

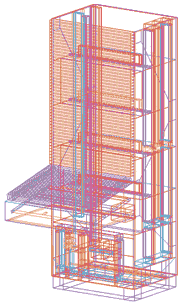
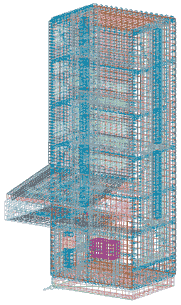
Рис. 1. CAD-модель	Рис. 2. Геометрическая модель	Рис. 3. Расчетная модель

Разумное упрощение CAD-модели является одним из эффективных инструментов повышения производительности анализа (рис. 2). Трансформация CAD-модели в расчетную, конечно-элементную модель (рис. 3) с учетом максимального использования конструкторских наработок производится в I-DEAS NX с применением специальных модулей предпроцессорной подготовки:

• Master Modeler, Master Assembly — построение специализированной геометрической модели (см. рис. 3);

• Meshing, Beam Sections — наложение дискретных сеток, построение конечно-эле­мент­ной модели (КЭМ);

• Boundary Conditions — наложение условий механического нагружения, условий закрепления, различных начальных условий;

• TMG Thermal Analysis — наложение тепловых связей, начальных условий теплопередачи.

Расчетные модули приложения Simulation системы I-DEAS NX позволяют произвести расчет напряженно-деформированного состояния, запасов прочности, собственных частот и форм колебаний, сделать анализ устойчивости, решить задачи теплопередачи, исследовать нелинейные статические процессы, динамические переходные процессы, проанализировать частотные характеристики при воздействии случайных нагрузок, спектральный анализ, анализ ресурса и долговечности:

• Model Solution — расчет в статической постановке задачи, расчет на устойчивость, расчет собственных частот;

• Response Analysis — моделирование динамических процессов в конструкции;

• Durability — расчет долговечности и ресурса;

• TMG Thermal Analysis — расчет тепловых режимов при стационарных и нестационарных режимах.

I-DEAS NX позволяет провести оптимизацию конструкций (модуль Optimization) для задач статики, устойчивости, установившихся и неустановившихся динамических процессов, собственных частот и форм колебаний. Вес, напряжения, перемещения, собственные частоты и многие другие характеристики могут рассматриваться в качестве либо целевых функций, либо ограничений.

Модули отображения результатов и постпроцессоры системы I-DEAS NX обеспечивают средства для изображения и интерпретации результатов после окончания решения:

• Post Processing — анализ полученных результатов, визуализация распределения силовых реакций, напряжений, деформаций, тепловых полей и др.;

• Durability, Response Analysis — оценка долговечности, динамических откликов, кинематических параметров конструкции.

Необходимость верификации вычислительных алгоритмов

Оценка механической прочности производится с применением метода конечных элементов (МКЭ), реализованного в I-DEAS NX.

Основным этапом расчета конструкций МКЭ является вывод матриц жесткости. Свойства матриц жесткости во многом определяют существование, устойчивость и сходимость решений МКЭ, а также эффективность метода в целом. Наиболее распро­страненный способ получения матриц жесткости основан на применении процессов Ритца или Галеркина специально для кусочно-гладких координатных функций. При этом перемещения точек внутри конечных элементов (КЭ) аппроксимируются интерполяционными полиномами с таким расчетом, чтобы контакт элементов в узловых точках обеспечивал неразрывность функций перемещений во всем теле. Многолетний опыт решения задач механики деформируемых твердых тел на основе МКЭ показал, что указанный вариант нередко обладает сравнительно медленной сходимостью, в особенности для оболочек и массивных тел сложных криволинейных форм. Замедленная сходимость характерна для тех случаев, когда принятый вариант аппроксимации перемещений не позволяет точно описать смещения КЭ как жесткого целого.

Исходя из вышеперечисленного для решателей коммерческих CAE-систем, в документации к которым скрыты или недостаточно полно приведены механизмы физико-математического моделирования КЭ, требуется проведение верификационных исследований вычислительных алгоритмов. Данные исследования также необходимы в случае использования решателя CAE-системы для виртуального моделирования и инженерных расчетов объектов атомной энергетики (конструкции ПТС), ввиду высоких требований к точности расчетов таких конструкций.

Результаты верификации на примере типовых конструкций ПТС

Целью верификационных исследований является аттестация алгоритмов I-DEAS на предмет возможности ее использования для расчетов прочности и стойкости оборудования, конструкций ПТС при воздействии эксплуатационных нагрузок. Предмет исследования — определение степени адекватности расчетов параметров напряженно-деформированного состояния и собственных частот тестовых конструкций алгоритмами I-DEAS и аналитическими методами.

Объектами исследования для проведения инженерных расчетов являются следующие:

• конструкции ПТС АСУ ТП АЭС;

• изделия электронной и вычислительной техники;

• электротехническое оборудование;

• контрольно-измерительные приборы и приборы автоматики;

• блоки и узлы приборов;

• элементы, встроенные в перечисленные виды оборудования.

Согласно теоретическим обоснованиям и разработанной методике исследования характеристик точности решателя I-DEAS следует:

• в качестве характеристики точности решателя при проведении прочностных статических расчетов конструкции принять степень соответствия значений параметров напряженно-деформированного состояния (НДС), полученных решателем и эталонным методом;

• при проведении прочностных динамических расчетов в качестве характеристики точности решателя принять степень соответствия значений собственных частот конструкции, полученных решателем и эталонным методом;

• за критерий оценки соответствия принять величину относительной погрешности параметров расчета решателем относительно эталонного метода;

• определить необходимый объем тестовых конструкций для подтверждения достаточности проводимых исследований характеристик точности решателя на предмет возможности его использования при расчетах прочности и стойкости оборудования АЭС к экс­плуатационным нагрузкам.

Выбор типов тестовых конструкций, их геометрических и физических параметров был произведен с учетом того, что они должны:

• быть по условиям своей работы аналогами элементов несущих конструкций оборудования АЭС;

• иметь запас прочности, отвечающий требованиям механической стойкости оборудования АЭС к эксплуатационным статическим воздействиям;

• иметь спектр собственных частот, отвечающий требованиям механической стойкости оборудования АЭС к эксплуатационным и сейсмическим воздействиям;

• обеспечивать моделирование динамических свойств и НДС в пределах линейной теории упругости.

Модели тестовых конструкций были представлены в виде:

• тонких пластин с прямоугольной и круглой формами контура, различающимися геометрическими размерами и толщиной;

• прямолинейных и криволинейных балок разной длины с постоянным сечением прямоугольной формы;

• толстостенных цилиндров постоянной толщины.

Соответствие условий работы моделей тестовых конструкций и элементов несущих конструкций оборудования АЭС обеспечивалось следующими условиями закрепления:

• шарнирное закрепление;

• жесткая заделка;

• свободный край.

В процессе создания КЭМ тестовых конструкций использовались КЭ из библиотеки системы I-DEAS:

• Beam-Linear — линейный балочный элемент;

• Beam-Curved — квадратичный балочный элемент;

• Thin Shell — Linear Quadrilateral — тонкая пластина, линейный четырехугольник;

• Thin Shell — Parabolic Quadrilateral — тонкая пластина, квадратичный четырехугольник;

• Solid — Linear Brick — линейный трехмерный элемент;

• Solid — Parabolic Brick — квадратичный трехмерный элемент.

Относительная погрешность расчета решателем I-DEAS определялась в соответствии с выражением:

.

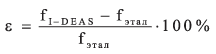Эталонные значения параметров НДС и собственных частот тестовых конструкций рассчитывались аналитическими методами по классическим методикам¹.

В результате исследования тестовых конструкций в виде прямолинейных консольных балок прямоугольного сечения высотой h, шириной b, отличающихся друг от друга длиной L, нагруженных сосредоточенной силой Р на конце (рис. 4), были получены данные, приведенные в таблице.

Рис. 4. Тестовая задача — прямолинейная консольная балка

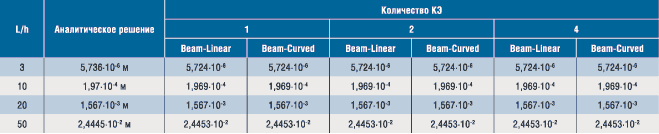
Как следует из приведенных результатов, практически точное решение получается при аппроксимации балки одним конечным элементом, используемым в системе I-DEAS.

На тестовой конструкции в виде рассеченного кольца радиусом R, прямоугольного сечения b x h с одним защемленным, а другим свободным от внешних связей концом, нагруженным сосредоточенной силой, оценивалась точность определения величины перемещения свободного конца бруса по направлению силы Р (рис. 5).

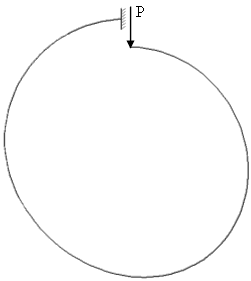
Рис. 5. Тестовая задача — рассеченное кольцо

Анализ результатов показал, что практически точное решение получается при ап­проксимации бруса восемью КЭ типа Beam-Curved. При использовании прямолинейных элементов Beam-Linear (окружность заменяется вписанным многоугольником) искажение геометрии приводит к ухудшению решений, что особенно существенно для редких сеток (рис. 6). Однако начиная с 32 КЭ результаты по обоим вариантам КЭ-моделей быстро сближаются и практически совпадают с аналитическим решением.

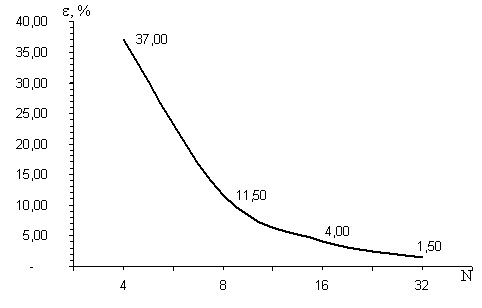
Рис. 6. Зависимость относительной погрешности определения перемещения свободного конца бруса от количества КЭ типа Beam-Linear

На тестовых конструкциях (рис. 7) в виде тонких плоских пластин квадратной формы, постоянной толщины h с жесткой заделкой по контуру при воздействии равномерно распределенной нагрузки или сосредоточенной в центре силы оценивалась точность определения максимального прогиба.

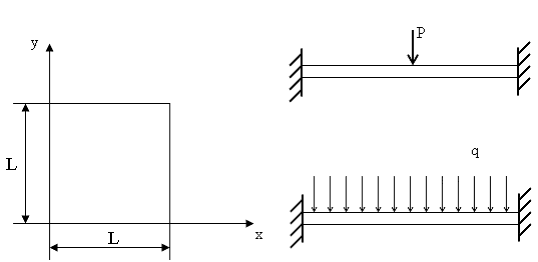
Рис. 7. Тестовая задача — плоская пластина с жесткой заделкой по контуру

В ходе исследований варьировались размеры стороны пластины и густота сетки КЭ. При численном моделировании данной задачи использовались КЭ типа Thin Shell — Linear Quadrilateral и Thin Shell — Parabolic Quadrilateral системы I-DEAS. В результате проведенных исследований можно сделать вывод, что при использовании КЭ типа Thin Shell — Parabolic Quadrilateral получается практически точное значение максимального прогиба пластин для всех рассмотренных вариантов расчетов. Максимальное значение относительной погрешности 4,8% получено на сетке 4x4 КЭ для пластины с L/h = 20, имеющей равномерно распределенную нагрузку. Изменение относительной погрешности в зависимости от количества КЭ типа Thin Shell — Linear Quadrilateral изображено на рис. 8 — для пластин, нагруженных равномерно распределенной нагрузкой, и на рис. 9 — для пластин, нагруженных сосредоточенной силой в центре.

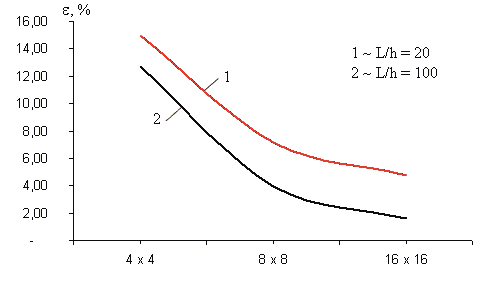
Рис. 8. Изменение относительной погрешности в зависимости от количества КЭ для пластин, нагруженных равномерно распределенной нагрузкой

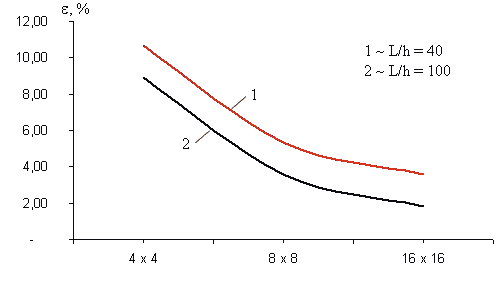
Рис. 9. Изменение относительной погрешности в зависимости от количества КЭ для пластин, нагруженных сосредоточенной силой в центре

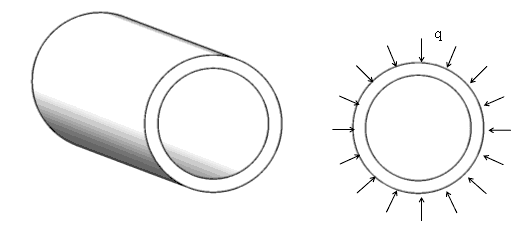
Рис. 10. Тестовая задача — сжатие толстостенного цилиндра

При численном решении тестовой конструкции (рис. 10) в виде толстостенного цилиндра с наружным радиусом b = 12 см и внутренним а = 6 см, при равномерном наружном давлении q = 10⁵ Па (задача Ламе) оценивалась точность определения окружных напряжений _t, радиальных напряжений _r и радиальных перемещений u_r в среднем поперечном сечении цилиндра. Длина образующей цилиндра бралась равной 2b и разбивалась на 11 КЭ, что обеспечивало независимость решения в рассматриваемом сечении цилиндра от граничных условий на его концах. По окружности сетка КЭ во всех проведенных расчетах состояла из 26 элементов. Численные решения получены с использованием КЭ типа Solid — Linear Brick и Solid — Parabolic Brick. В ходе расчетов варьиро­валось количество КЭ по толщине цилиндра.

Анализ результатов, полученных на тестовой конструкции в виде толстостенного цилиндра, показал, что во всех рассмотренных случаях численные решения для радиальных перемещений, полученные с помощью системы I-DEAS, практически совпадают с аналитическим (максимальная погрешность — 1,5%). Различие состоит только в том, что при использовании в численных расчетах КЭ типа Solid — Linear Brick, строго говоря, можно анализировать только интегральные характеристики решения — перемещения и усиления. При оценке локальных характеристик — деформаций и напряжений — необходимо использовать КЭ типа Solid — Parabolic Brick. Так, например, граничные условия по напряжениям на внешней поверхности цилиндра при использовании КЭ Solid — Parabolic Brick удовлетворяются с точностью 1%. При использовании в численных расчетах 6 КЭ типа Solid — Linear Brick эта ошибка составляет 3,1%, а при 3 КЭ — уже 6,35%.

Степень соответствия значений собственных частот проверялась на балках с различными вариантами закрепления, а также на тонких пластинах с прямоугольной и круглой формами контура. Формы колебаний тестовых конструкций приведены на рис. 11 и 12.

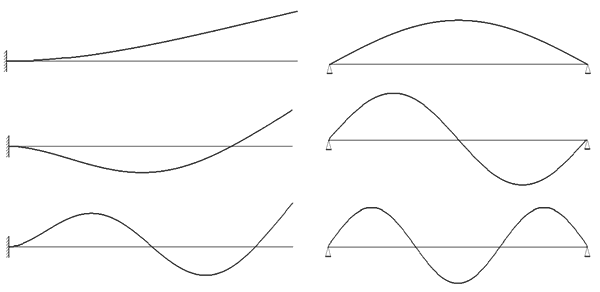
Рис. 11. Формы колебаний балок при различных вариантах крепления

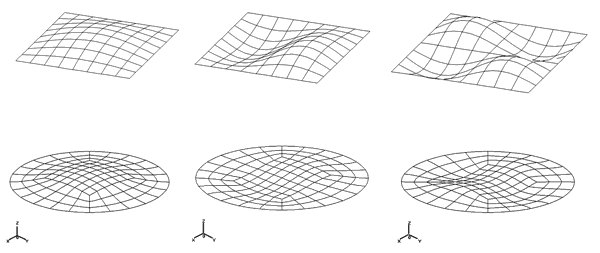
Рис. 12. Формы колебаний пластин с прямоугольной и круглой формами контура

В ходе исследований варьировались размеры балок, пластин и густота сетки КЭ. При численном моделировании использовались КЭ первого и второго порядка семейства Thin Shell и Solid для построения КЭМ-пластин. Для моделирования балок использовались КЭ типа Beam-Linear и Beam-Curved. Пример результатов расчета относительных погрешностей собственных частот шарнирно закрепленной по контуру квадратной пластины, смоделированной КЭ типа Thin Shell — Parabolic Quadrilateral, приведен на рис. 13.

Анализ результатов показал, что функция относительной погрешности расчета собственных частот не значительно зависит от плотности сетки КЭ для всех вариантов тестовых конструкций. С увеличением численного значения рассчитываемой резонансной частоты относительная погрешность возрастает и в худшем случае составляет не более 5%.

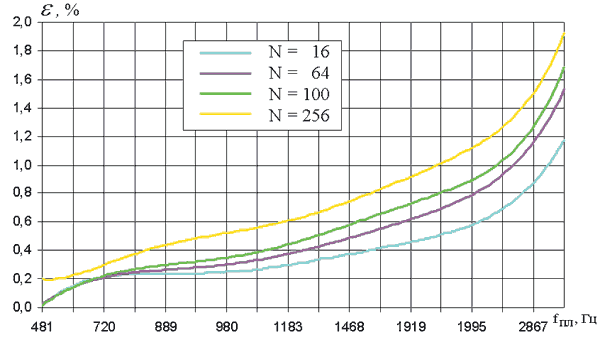
Рис. 13. Изменение относительной погрешности в зависимости от количества КЭ Thin Shell — Parabolic Quadrilateral при анализе собственных частот шарнирно закрепленной по контуру квадратной пластины

Заключение

Из результатов анализа характеристик точности расчета тестовых конструкций алгоритмами I-DEAS следует, что уровень относительных погрешностей расчета контролируемых параметров прочности и стойкости зависит как от конструктивного исполнения и краевых условий закрепления, так и от способа моделирования конечно-элементной сетки, включающего ее плотность и применяемый тип конечных элементов. При наихудших условиях относительная погрешность численных методов от аналитических составляет не более 5%, что является приемлемым результатом.

Проведенные исследования точности вычислительных алгоритмов, а также сравнительный анализ результатов численных исследований с результатами натурных испытаний позволили разработать обоснование распространимости результатов испытаний опытных образцов конструкций ПТС на соответствующие ряды идентичных конструкций. Дальнейшее накопление статистических данных позволило разработать методику проведения расчетно-экспериментальной отработки объектов ПТС на подтверждение требованиям технического задания (ТЗ) к воздействию внешних факторов. Согласно данной методике натурные испытания проводятся для одной базовой конструкции соответствующего модельного ряда, а для всех остальных модификаций испытания заменяются расчетами в I-DEAS.

Таким образом, отсутствует необходимость в проведении дорогостоящих натурных испытаний опытного образца новой модификации ПТС, если эксплуатационно-конструкторские характеристики изделия попадают в один из пяти типорядов основных конструкций, опытные образцы которых прошли весь цикл предварительных испытаний на подтверждение конструкторских гарантий. За период с 2001-го по 2004 год лишь 9 единиц оборудования были подвергнуты натурным испытаниям на стойкость к внешним воздействующим факторам, при этом по результатам компьютерного моделирования 263 изделиям присвоена литера О 1 и они успешно эксплуатируются на объектах атомной энергетики. Из данного модельного ряда ПТС только 29 изделий имеют один и тот же децимальный номер, а остальные — индивидуальны в своем обозначении, а следовательно, и в исполнении. Надзорные органы в лице ФГУП «ВО Безопасность» и «Ростехнадзора», контролирующие ход разработки и изготовления ПТС для АЭС, принимают расчетно-аналитические подтверждения выполнения требований ТЗ на ПТС, выполненные с использованием модулей инженерного анализа системы I-DEAS.

Следует подчеркнуть, что цикл предварительных (натурных) испытаний одного опытного (головного) образца длится до 3 месяцев, финансовые затраты составляют несколько сотен тысяч рублей. Только благодаря расчетным обоснованиям (применению процедур виртуального моделирования в CAE-системе I-DEAS) стойкости ПТС к внешним воздействующим факторам экономия финансовых ресурсов для разработчика ПТС — ФНПЦ ФГУП «НИИ измерительных систем» — составила порядка 5 млн. рублей при разработке и изготовлении оборудования АСУ ТП для российских и зарубежных АЭС с выполнением календарных сроков поставки в соответствии с требованиями контрактов.

---

¹Аналитические методы расчета приведенных тестовых задач описаны в следующих пособиях:

• Метод конечных элементов в механике твердых тел / Под ред. А.С.Сахарова, И.Альтенбаха. Киев: Вища школа, 1982.

• Прочность, устойчивость, колебания: Справ. в 3 т. Том 1 / Под ред. И.А.Биргера, Я.Г.Паповко. М.: Машиностроение, 1968.

• Тимошенко С.П., Войновский-Кригер С. Пластинки и оболочки. М.: Наука, 1966.

• Тимошенко С.П. Колебания в инженерном деле. М.: Наука, 1967.

• Федосьев В.И. Сопротивление материалов. М.: Наука, 1979.

САПР и графика 7'2005