Проект ERGO: начало пути

Александр Данилин, Николай Зуев

Как все начиналось

Сущность нового подхода

Тестовые примеры

   Задача 1. Деформирование консольной балки при действии сосредоточенного моментаи

   Задача 2. Деформирование балки при действии двух моментов

   Задача 3. Система четырех стержней

   Задача 4. Система пяти стержней

   Задача 5. Длинная пластина под действием момента на свободном конце

Приглашаем к сотрудничеству

Ж урнал «САПР и графика» неоднократно рассказывал о программных разработках компании «ТЕСИС» (см. № 4 и 9 за 1999 год, № 7 за 2000 год). Сегодня мы предлагаем вниманию читателей нашу новую программу ERGO для решения задач механики деформируемого твердого тела по методу конечных элементов (МКЭ).

Как все начиналось

На протяжении многих лет группа ученых Московского государственного авиационного института (впоследствии технического университета), возглавляемая доктором физ. мат. наук профессором В.И.Шалашилиным, занимается разработкой новых методов численного решения нелинейных задач механики деформируемого твердого тела. В результате создана новая и, как мы считаем, существенно более качественная методика решения таких задач.

Понятно, что путь от плодотворной научной идеи до коммерческого программного продукта непрост и чреват многими неожиданностями. Но — «дорогу осилит идущий»: в конце прошлого года совместно с компанией «ТЕСИС» был начат научно-исследовательский проект ERGO (ergo — от лат. следовательно) . В его рамках создана программа, позволяющая решать плоские геометрически и физически нелинейные статические задачи с использованием новых подходов в рамках МКЭ. Кроме того, ERGO позволяет исследовать линейные статические и динамические задачи. Для создания модели и анализа результатов применяется хорошо известный многим российским исследователям и инженерам пре/постпроцессор FEMAP.

Программа разрабатывается авторами статьи и преподавателями МАИ кандидатом физ.-мат. наук доцентом А.Б.Костриченко и профессором В.И.Шалашилиным.

Сущность нового подхода

Моделирование геометрически и физически нелинейных задач механики деформируемого твердого тела по методу конечных элементов сводится к решению системы нелинейных алгебраических уравнений.

Процесс нахождения решения такой системы можно выполнять методом продолжения по параметру: решение строится от исходного (недеформированного) состояния до достижения заданного уровня нагружения. В качестве параметра продолжения p обычно выбирают параметр нагрузки или длину дуги интегральной кривой в пространстве «перемещение — параметр нагрузки» (второй вариант, называемый методом длины дуги, более предпочтителен, поскольку обеспечивает максимальную локальную обусловленность в окрестности каждой точки интегральной кривой).

Таким образом, требуется найти решение системы нелинейных алгебраических уравнений

(1)

при 0≤p≤P (где P соответствует конечному состоянию системы), причем из физической сущности задачи известно, что при p = 0 решение .

Для нахождения промежуточных состояний при приращении параметра p используются известные численные процедуры, например метод Ньютона-Рафсона. Такой подход, называемый методом дискретного продолжения по параметру, используется во всех известных нам коммерческих расчетных системах, в частности ABAQUS, NASTRAN, Cosmos/M, ANSYS.

К недостаткам изложенного подхода относится большое количество настроек решателя. Например, в программном комплексе UAI/NASTRAN пользователь должен задать около 20 параметров, управляющих стратегией продолжения решения и итерациями на каждом шаге. По собственному опыту мы знаем, что в ряде случаев подбор параметров, обеспечивающих нахождение решения, является весьма непростой задачей.

Существует альтернативный вариант поиска решения задачи (1). Для этого необходимо записать дифференциальный аналог (1) по параметру продолжения. Процедура проста: следует продифференцировать (1) по параметру p. В результате система нелинейных алгебраических уравнений преобразуется к следующей задаче Коши для системы обыкновенных дифференциальных уравнений относительно переменной p:

(2)

причем 0<p<P, u(0) = 0.

Такой подход к решению систем нелинейных алгебраических уравнений, предложенный в 50-х годах Д.Ф.Давиденко, называется методом непрерывного продолжения решения по параметру. В этом случае для решения используются хорошо исследованные и разработанные методы численного интегрирования задачи Коши, которые не требуют сложных настроек (пользователь должен задать только допустимую локальную погрешность), что обеспечивает высокую устойчивость вычислительного процесса. Как показало решение многих примеров, для численного интегрирования задачи (2) достаточно использовать явные методы семейства Рунге-Кутта с переменным шагом.

Научная новизна разработок, ставших основой ERGO, заключается в новой математической формулировке конечноэлементного подхода (по сравнению с методом непрерывного продолжения по параметру), разработке конечных элементов и рациональном выборе параметра продолжения.

Тестовые примеры

В настоящее время решено достаточно много задач. Наиболее интересно применение ERGO для решения статических нелинейных задач. Ниже приведены некоторые из рассмотренных геометрически нелинейных задач и полученные решения1 .

Задача 1. Деформирование консольной балки при действии сосредоточенного момента

Аналитические результаты

Точной формой деформирования упругой линии балки является дуга окружности радиуса R = EI/M, где EI — изгибная жесткость поперечного сечения. При EI = 20 Н×м², L = 10 м и M = (16π) Н×м ≈ 50,2655 Н×м балка сворачивается в кольцо радиуса R = L/(8π), то есть нагруженный конец делает четыре оборота, поворачиваясь на угол 8π рад ≈ 25,1327 рад.

Результаты ERGO

Значение угла поворота нагружаемого узла, полученное в результате расчета, отличается от точного на 0,04%. Расчетная модель имеет 120 степеней свободы; процессорное время расчета на компьютере Pentium II 350 МГц — 3 мин 38 с.

Задача 2. Деформирование балки при действии двух моментов

Аналитические результаты

При тех же геометрических и жесткостных параметрах, что и в первом примере, и M = (8π) Н×м ≈ 25,1327 Н×м форма деформирования — «восьмерка» (нагружаемые узлы в конечном состоянии должны совпасть с заделкой).

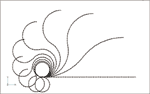Результаты ERGO

Расстояние между заделанным и нагруженными узлами в конечном положении оказалось менее 0,05 мм при величине полного перемещения 5 и 10 м. Расчетная модель имеет 120 степеней свободы, время расчета 3 мин 24 с.

Задача 3. Система четырех стержней

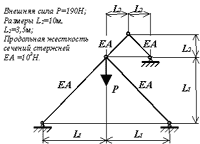Аналитические результаты

Исходя из условий равновесия установлено, что два верхних стержня в конечном состоянии вытягиваются в линию, а нагружаемый узел смещается вниз и вправо.

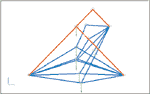Результаты ERGO

Конечному состоянию системы на рисунке соответсвует низшее положение нагружаемого узла. Расчетная модель содержит четыре степени свободы, время расчета — 0,2 с.

Задача 4. Система пяти стержней

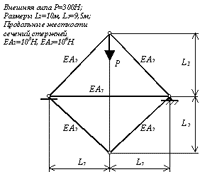Аналитические результаты

Исходя из условий равновесия установлено, что верхние стержни не прощелкиваются, то есть нагружаемый узел остается выше нижних растянутых стержней.

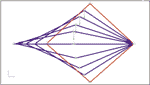Результаты ERGO

Конечному состоянию системы на рисунке соответствует низшее положение нагружаемого узла. Расчетная модель содержит пять степеней свободы, время расчета — 0,9 с.

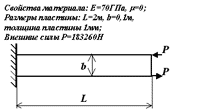
Задача 5. Длинная пластина под действием момента на свободном конце

Аналитические результаты

Момент моделировался парой следящих сил, для сохранения плеча между нагружаемыми узлами введен жесткий стержень. В качестве приближения к строгому решению используется балочное решение (см. задачу 1). При выбранных параметрах балочное приближение дает поворот нагружаемого сечения 2π рад ≈ 6,2832 рад.

Результаты ERGO

Значение угла поворота нагружаемого узла, полученное в результате расчета, отличалось от балочного решения на 0,55%. Расчетная модель содержит 6741 степень свободы. Время расчета — 6 ч 58 мин.

Отметим, что все задачи решены с первой попытки без утомительного подбора настроек решателя.

Приглашаем к сотрудничеству

Апробация новых научных идей на практике — дело непростое. Поэтому в начале мая 2000 года мы пригласили всех желающих принять участие в тестировании решателя ERGO 3.0.

Несколько десятков человек скачали дистрибутив ERGO с нашего сайта. Как показало время, программа оказалась интересна исследователям и инженерам. Преподаватели вузов получили эффективное и, что немаловажно, бесплатное средство для применения в учебном процессе, а студенты — возможность ознакомиться с современной программной реализацией метода конечных элементов и особенностями нелинейного анализа.

На момент написания статьи заканчивается тестирование версии ERGO 4.0, в которую заложен ряд новых возможностей (следящие нагрузки, нелинейно-упругие материалы и т.д.) В сентябре текущего года новая версия должна появиться на нашем сайте.

Мы приглашаем всех заинтересованных специалистов принять участие в тестировании программы ERGO. Бесплатно распространяемую версию программы ERGO и демо-версию пре/постпроцессора FEMAP вы можете получить на сайте ООО «ТЕСИС» http://www.tesis.com.ru/, либо направив запрос по электронной почте nz@tesis.com.ru.