Введение в моделирование динамики механических систем
Для чего нужно компьютерное моделирование
Анализ динамики в проектировании механических систем
Программный комплекс «Универсальный механизм»
Опыт использования УМ на Электростальском заводе тяжелого машиностроения (ЭЗТМ)
Опыт использования УМ на ФГУП «ПО Уралвагонзавод»
Введение
В отличие, например, от прочностных расчетов методом конечных элементов, которые давно вошли в обычную практику инженеров-исследователей, динамические расчеты с помощью специализированного программного обеспечения до сих пор в силу многих причин не стали непременным атрибутом инженерного анализа. Сложившееся положение дел усугубляется отсутствием специалистов, которым просто неоткуда взяться: в технических вузах практически нет специализированных курсов, соответственно на предприятиях нет сложившихся традиций и опыта использования подобного программного обеспечения. Самостоятельному изучению препятствует дефицит специализированных материалов, круг которых в настоящее время ограничен руководствами пользователя к соответствующему программному обеспечению.
В настоящей статье обсуждаются предпосылки, основные принципы и понятия, связанные с компьютерным моделированием динамики механических систем; ее можно рассматривать как своего рода введение в предмет.
Для чего нужно компьютерное моделирование
В настоящее время общепринято мнение о том, что изучение динамики механической системы может быть выполнено путем комбинации физических экспериментов и компьютерного моделирования. Если есть доступный экспериментальный образец механической системы, то можно поставить ряд физических экспериментов и определить интересующие характеристики этого объекта. Измеряемые динамические характеристики обычно включают линейные и угловые перемещения, скорости и ускорения, усилия между элементами конструкции, а также между механизмом и внешними по отношению к нему объектами (фундаментом машины, автомобильным мостом, железнодорожными путями и т.д.).
Для определения различных динамических показателей на разных режимах работы механической системы обычно требуется поставить большое число физических экспериментов, а также оснастить испытательную площадку сложным и обычно дорогим измерительным и регистрирующим оборудованием. Объем работ по подготовке механизма к испытаниям, по установке и настройке измерительного оборудования, обработке и изучению полученных результатов значителен, а стоимость таких работ высока. Вместе с тем при проведении физических экспериментов не всегда возможно измерение всех интересующих динамических показателей — приходится преодолевать проблемы, связанные с погрешностями измерительных приборов, повторяемостью и воспроизводимостью результатов. Кроме того, испытания машин на предельных или нештатных режимах, как правило, либо очень дорогостоящи в силу дороговизны образцов или оборудования, которые разрушаются, либо опасны, как эксперимент, показанный на рис. 1а.
 a
a
 b
b
Рис. 1. Проведение некоторых натурных экспериментов с автопоездом связано с опасностью его переворота и требует оснащения аутригерами: а — натурный эксперимент; б — компьютерное моделирование (ил. взята из изд.: Winkler C.B., Blower D., Ervin R.D., Chalsani R.M. Rollover of Heavy Commercial Vehicles: SAE Research Report. Warrendale: Society of Automotive Engineers, Inc.)
Компьютерное моделирование — привлекательная замена физическим экспериментам, поскольку не требует изготовления экспериментального образца; с помощью компьютерного моделирования может быть поставлено любое число численных экспериментов и получены любые интересующие исследователя динамические показатели. Компьютерные модели могут быть использованы для выявления и устранения проблем еще до производства первого образца, что особенно важно для штучных и мелкосерийных производств.
В сравнении с натурными экспериментами компьютерное моделирование — очень полезный инструмент, который обеспечивает всесторонний, рентабельный и безопасный анализ динамики механических систем. Это дает возможность с минимальными затратами подвергать тщательному анализу, в том числе, совершенно новые идеи и решения.
Сложность динамического анализа заключается в невозможности точного аналитического исследования даже простых механических систем, поскольку динамика, как правило, описывается системами дифференциальных или дифференциально-алгебраических уравнений, в общем случае нелинейных, решение которых аналитически получить невозможно. Однако само составление уравнений движения механических систем с большим числом степеней свободы может оказаться очень непростой процедурой. Это связано с ростом сложности выражений для кинематических величин, определяющих положение, скорости и ускорения тел, входящих в систему, при увеличении длины кинематических цепей. Кроме того, постоянный рост требований к качеству проектируемых технических систем приводит к необходимости построения усложненных динамических моделей. С одной стороны, это влечет за собой увеличение числа степеней свободы, а следовательно, приводит к упомянутым выше проблемам. С другой стороны, уточняются и усложняются математические модели сил взаимодействия тел, входящих в систему. Примерами могут служить силы взаимодействия железнодорожного колеса с рельсом и автомобильного колеса с дорогой. Наконец, наблюдается тенденция к сокращению сроков, необходимых для создания новой техники. В силу описанных здесь причин возможности аналитических методов исследования динамики механических систем резко ограничены и в современных условиях для решения таких задач применяется специализированное программное обеспечение.
Анализ динамики в проектировании механических систем
Типовой анализ механических систем в машиностроении включает, как правило, анализ динамики, прочности и долговечности. В идеале процесс проектирования идет итерационно и начинается с эскизного проекта, который определяет основные геометрические, инерционные и прочие параметры системы. Далее строится ее динамическая модель, с помощью которой, например, выполняется параметрическая оптимизация и определяются динамические показатели системы, которые в ряде отраслей могут быть ограничены различными нормами и стандартами. Кроме того, с помощью динамической модели определяются усилия взаимодействия между элементами конструкции в шарнирах, сочленениях, опорах, силовых (пружинах, рессорах, демпферах) и крепежных элементах на штатных и экстремальных режимах работы. Определенные здесь усилия являются входными данными для дальнейшего анализа деталей механической системы на прочность и долговечность. Если по результатам анализа прочности и долговечности заметно меняются геометрические или инерционные параметры системы, выполняется повторный анализ динамики, который уточняет величины усилий при новых значениях параметров, а затем повторяются остальные виды анализа.
Вместе с тем не стоит рассматривать динамический анализ только как инструмент, позволяющий определять нагрузки для дальнейшего прочностного анализа. Во многих случаях, например для транспортных средств, он имеет выраженное самостоятельное значение.
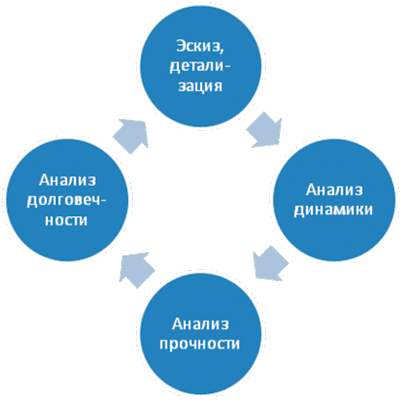
Методика моделирования
Рассмотрим общие принципы работы инженеров-исследователей с программным обеспечением для моделирования динамики механических систем. Как и в любой другой области моделирования, после постановки задачи при построении модели исследователь переходит от реального объекта к его идеализированной расчетной схеме. Искусство исследователя заключается в умении построить не самую сложную, но адекватную расчетную схему, которая позволила бы решить поставленную задачу наиболее эффективно.
В основе моделирования динамики механических систем лежит их представление системой связанных абсолютно твердых или упругих тел. Наиболее универсальным способом описания положения и возможных движений пары тел, одним из которых может быть неподвижная система координат, является использование понятия шарнира. Современное коммерческое программное обеспечение дает возможность ввести в модель любые шарниры, встречающиеся на практике.
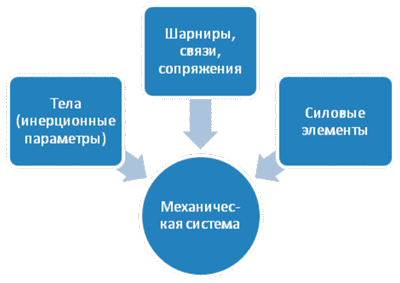
Особое значение имеет описание силовых элементов, определяющих взаимодействия пар тел. От полноты базы встроенных силовых элементов зависит применимость той или иной программы в каждом конкретном случае. Вместе с тем отметим, что модели таких типовых сил, как пружина или демпфер, есть в любой программе, представленной на рынке. Принципиальные для пользователя отличия начинаются в проблемно-ориентированных моделях сил, таких, например, как силы взаимодействия железнодорожного колеса и рельса, автомобильного колеса и дороги, гусеницы и грунта и т.д. Отметим также, что практически во всех программах есть возможность описания пользователем собственных математических моделей сил на специализированном встроенном или обычном алгоритмическом языке программирования и включение таких сил в построенные модели механических систем.
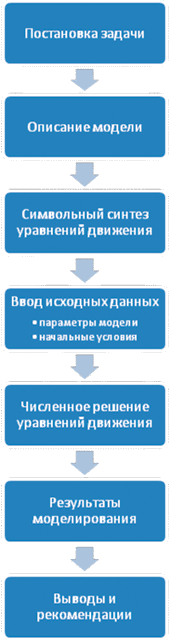
После описания модели явно или неявно для пользователя происходит этап автоматического синтеза уравнений движения механических систем с помощью специальных алгоритмов. Программная реализация таких алгоритмов может быть выполнена как в символьной, так и в численно-итерационной форме. Символьный синтез уравнений движения предполагает вывод уравнений на одном из языков программирования (обычно поддерживаются Fortran, C и Pascal). Далее эти синтезированные файлы должны быть откомпилированы внешним компилятором, что на выходе дает исполняемые файлы, готовые к использованию. Численно-итерационный метод предполагает формирование уравнений движения численно на каждом шаге численного метода интегрирования уравнений движения. Формирование уравнений движения в символьной форме позволяет эти уравнения оптимизировать с точки зрения количества арифметических операций1, что обеспечивает заметные преимущества по быстродействию процесса моделирования, а численно итерационные алгоритмы дают возможность проще организовывать моделирование систем с переменной структурой.
Целью компьютерного моделирования технической системы является анализ ее свойств с использованием построенной модели. Основной инструмент такого анализа — численное интегрирование нелинейных уравнений движения. Отметим основные требования к методам, используемым в коммерческом программном обеспечении. Во-первых, это возможность интегрировать с автоматическим выбором шага и контролем точности решения. Во-вторых, способность эффективно решать так называемые жесткие уравнения, то есть уравнения, в которых наряду с медленными есть очень быстро протекающие процессы; классические численные методы для таких систем практически не подходят2.
По окончании численного моделирования в качестве результатов для дальнейшего анализа доступны следующие величины:
- кинематические характеристики (траектории, координаты, скорости, ускорения любой точки любого тела, углы поворотов, угловые скорости и угловые ускорения тел, характеристики относительного движения тел);
- силы реакций в шарнирах;
- активные силы (например, силы в пружине, гасителе колебаний, листовой рессоре, гидроцилиндре);
- напряжения и деформации для упругих тел.
Рис. 2. Гибридная модель подвески грузовика (а) и результаты расчета долговечности рамы тележки локомотива (б) в ПК «Универсальный механизм»
Программный комплекс «Универсальный механизм»
В настоящее время на рынке программного обеспечения данное направление представлено довольно большим числом универсальных программ, например MSC.ADAMS, LMS.DADS, SYMPACK, а также программ, ориентированных на конкретные объекты3. Например, программы MEDYNA, NUCARS и Vampire ориентированы на моделирование динамики рельсовых экипажей. Все программы данного типа автоматизируют процесс формирования уравнений движения конкретной механической системы на основе описания инерционных, геометрических и кинематических параметров, моделей силовых взаимодействий, выбранных или заданных пользователем. Для дальнейшего исследования динамики объекта используются численные методы анализа уравнений движения, например численное интегрирование.
В России заметное распространение получил программный комплекс «Универсальный механизм» (УМ)4, разработанный в лаборатории вычислительной механики Брянского государственного технического университета. В настоящее время комплекс включает мощное универсальное ядро, отвечающее всем современным требованиям, и ряд специализированных модулей для моделирования динамики автомобилей (рис. 2а), железнодорожных экипажей, гусеничных машин, модули оптимизации, расчета долговечности (рис. 2б) и пр. Кроме того, программный комплекс имеет интерфейсы с другими программными продуктами. Например, модуль моделирования упругих тел поддерживает импорт данных из ANSYS и MSC.NASTRAN, модуль импорта 3D-моделей из CAD-программ сегодня поддерживает SolidWorks, КОМПАС, Autodesk Inventor и Pro/ENGINEER, модуль UM Control обеспечивает импорт моделей из Matlab/Simulink.
Далее рассмотрим несколько примеров использования УМ в реальной практике производственного предприятия.
Опыт использования УМ на Электростальском заводе тяжелого машиностроения (ЭЗТМ)
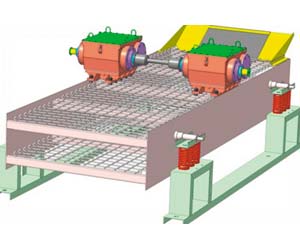
Широкая номенклатура новой техники, над которой в последние годы приходится работать специалистам предприятия, требует широкого внедрения средств автоматизации проектирования, в том числе программного обеспечения для инженерного анализа. Специфика некоторых проектируемых машин такова, что без предварительного анализа их динамики не обойтись. Речь идет, в частности, об инерционных грохотах (рис. 3а) и щековых дробилках (рис. 3б).
 a
a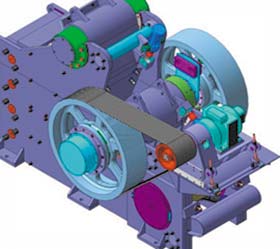 b
b
Рис. 3. Динамические модели проекта ЭЗТМ, импортированные из КОМПАС-3D: а — грохота; б — дробилки
Рассмотрим механизм грохота. Его назначение — при помощи сеток с ячейками разного размера разделять поступающую на него породу по фракциям и обеспечивать направленное движение частиц так, чтобы сепарированные потоки стекали с его противоположной стороны. Вращение дебалансов, установленных на валу вибратора, заставляет раму грохота вместе с неподвижно закрепленными на ней сетками совершать вынужденные колебания. Отношение амплитуд вертикального и продольного компонентов колебаний обеспечивает баланс между сепарированием и продольным перемещением фракций породы по сеткам грохота.
Проведенное сравнение показало, что результаты компьютерного моделирования в программном комплексе «Универсальный механизм» количественно и качественно практически полностью совпадают с результатами стендовых испытаний, относительная ошибка не превышает 5-10%. Созданная параметризованная динамическая модель грохота использовалась для проверки различных конструктивных решений, а также для определения оптимальных значений масс дебалансов и жесткостей рессорных комплектов.
Исторический экскурсДинамика систем тел как отдельная дисциплина базируется на принципах классической механики. Материальная точка, как наиболее простой объект исследования, удовлетворяет уравнениям Ньютона, которые были опубликованы в 1686 году в его работе «Philosophiae Naturalis Principia Mathematica». Понятие твердого тела было введено Эйлером в 1775 году в его труде «Nova methodus motum corporum rigidarum determinandi». Для учета действия связей и шарниров Эйлер использовал принцип замены действия связей их силами реакции. Полученные уравнения известны в механике как уравнения Ньютона — Эйлера. Механическая система впервые была рассмотрена в 1743 году Даламбером в его «Traite de Dynamique», где он провел различия между активными силами и силами реакции и ввел принцип, ныне носящий его имя. В 1788 году в работе «Mecanique Analytique» Лагранж провел анализ связанных механических систем, применив вариационные принципы к кинетической и потенциальной энергии механической системы, принимая во внимание кинематические связи между телами системы и выбранные обобщенные координаты, и получил в результате так называемые уравнения Лагранжа первого и второго рода. Уравнения Лагранжа второго рода — минимальный набор дифференциальных уравнений второго порядка, описывающих динамику механической системы. Несмотря на очевидные успехи, вплоть до 60-х годов прошлого века сложность решаемых задач была ограничена объективными причинами: нелинейные эффекты различной природы и неэффективные численные методы делали решение более или менее сложных задач чрезвычайно затруднительной процедурой, требующей большого объема ручного труда. Высокие требования на сложность моделей, в первую очередь для космической отрасли, и бурное развитие вычислительной техники привели к появлению нового раздела механики — динамики систем тел, в котором принципы классической механики были дополнены и расширены с точки зрения применения компьютерных алгоритмов синтеза и решения уравнений движения механических систем. Одни из первых алгоритмов (формализмов) компьютерного синтеза уравнений движения были предложены в 1965 году Хукером и Маргулисом и в 1967-м Роберсоном и Швертассеком. Кроме этих численных формализмов, развивались также методы символьного вывода уравнений движения. Один из первых таких методов был опубликован Шиленым и Кройцером в 1977 году. Первые законченные коммерческие программные продукты для моделирования динамики систем тел появились в 80-х годах прошлого столетия. |
Опыт использования УМ на ФГУП «ПО Уралвагонзавод»
В последнее время все сильнее обостряется конкурентная борьба на рынке железнодорожного подвижного состава. Производитель, который предложит отвечающий требованиям заказчика товар в минимальные сроки, займет на нем лидирующее положение. Существенно сократить период разработки изделия можно с помощью программ компьютерного моделирования режимов эксплуатационной нагруженности железнодорожного подвижного состава.
Если многие вагоностроительные предприятия уже давно приобрели и внедрили в практику конечно-элементные программные комплексы (ANSYS, NASTRAN и т.д.) и самостоятельно выполняют все необходимые расчеты, то динамический анализ пока остается весьма специфической областью.
Первый шаг в решении этой проблемы на ФГУП «ПО Уралвагонзавод» был сделан в 2002 году, когда учеными БГТУ и УрГУПС при содействии специалистов предприятия была создана математическая модель самой массовой грузовой тележки модели 18-100 (рис. 4).


Рис. 4. Тележка модели 18-100
Именно эта модель легла в основу унифицированной математической модели трехэлементной тележки в составе модели грузового вагона с возможностью использования ее для моделирования тележек типа 18-100, а также тележек, содержащих скользуны постоянного контакта, линейное и билинейное рессорное подвешивание, буксовые адаптеры, износостойкие полимерные элементы в клиновой системе, упругие связи, обеспечивающие жесткость тележки в плане. Параметризация компьютерной модели позволяет варьировать параметры модели, в том числе моделировать динамику вагонов с учетом износа различных элементов тележки.
На 2008 год запланированы полевые испытания, по результатам которых будут проводиться уточнение и идентификация параметров расчетной схемы динамической модели трехэлементной тележки модели 18-578. Создание такой математической модели в дальнейшем позволит специалистам ФГУП «ПО Уралвагонзавод» оценить динамику железнодорожного подвижного состава еще на стадии проектирования с последующим выходом на динамическую нагруженность и оценку его долговечности и ресурса.
Авторы выражают благодарность зам. гл. конструктора, начальнику КБ ЭЗТМ Н.А.Павлову и инженеру Е.В.Потапову за предоставленные материалы.
1Например, вынести за скобки общий множитель, привести подобные члены, исключить умножение на единицу и ноль.
2Строгое определение понятия жесткости и подробное рассмотрение особенностей различных численных методов можно найти, например, в кн.: Современные численные методы решения обыкновенных дифференциальных уравнений / Под ред. Дж. Холла, Дж. Уатта. М.: Мир, 1989.
3Список программного обеспечения для моделирования динамики механических систем можно найти, например, по адресу: http://real.uwaterloo.ca/~mbody.
4Подробности по адресу: http://www.umlab.ru/index_rus.htm.




