Моделирование резонатора пьезогироскопа в системе АРМ WinMachine
Описание резонатора балочного типа
Построение и анализ упрощенной модели резонатора
Построение и анализ уточненной модели резонатора
Статический расчет с использованием температурной аналогии
Государственное научное учреждение «НИИ ПМТ» проводит работы по фундаментальным и прикладным исследованиям в области создания и модифицирования перспективных материалов, разработки контрольно-диагностических методов, приборов и технологий, а также в области информационных технологий. В сфере исследований института — миниатюрные устройства электронной микроскопии, вакуумной техники, миниатюрные сенсоры и датчики различного назначения, в том числе малогабаритные вибрационные гироскопы.
В последние годы различными фирмами предложен большой ассортимент конструкций подобного рода датчиков. Принцип их действия, как и классических роторных гироскопов, основан на возникновении кориолисовых сил инерции при вращении в инерциальном пространстве устройства с вибрирующими массами. Сфера применения датчиков довольно широкая — от автономной навигации до стабилизации движения и платформ.
В пьезогироскопах для возбуждения колебаний вибратора и получения сигнала о вращении используются соответственно обратный и прямой пьезоэффекты. Пьезоэлектрические датчики относятся к электронно-механическим устройствам резонансного типа. Важными параметрами, определяющими качество их работы, являются собственные частоты, амплитуды колебаний, добротность при малых габаритах и низкой стоимости производства.
Выбор современных программных средств для моделирования и расчета конструкций электронной техники является довольно сложной задачей в силу специфики самих объектов. Мы используем систему APM WinMachine, разрабатываемую научно-техническим центром АПМ (г.Королев, Московская обл.). Наш институт применяет программные продукты, выпущенные этой компанией, для расчета различных конструкций в учебных и научных целях уже более трех лет.
Данная статья посвящена исследованию резонаторов вибрационных пьезогироскопов методом конечных элементов. Приведен анализ модели резонатора балочного типа.
Задача исследований состоит в выборе из бесконечного спектра собственных форм и соответствующих собственных частот резонатора тех форм колебаний и частот, которые отвечают рабочему режиму гироскопа. В статическом режиме определяются перемещения и механические напряжения в элементах конструкции при заданных электрических напряжениях на пьезоэлементах.
В системе APM WinMachine версии 9.3 непосредственно учесть пьезоэффект при моделировании невозможно. Однако с появлением возможности решать тепловые задачи для учета деформаций пьезоэлементов была использована температурная аналогия. Основанием для такого подхода служит идентичность аддитивных членов в обобщенном законе Гука для свободной температурной деформации αT и для планарной пьезоэлектрической деформации βU пьезокерамической пластинки, поляризованной по толщине.
Поясним: α — температурный коэффициент линейного расширения; T — изменение температуры; β = d31/h — пьезоэлектрический коэффициент линейного расширения, зависящий от пьезомодуля d31 и толщины h пьезоэлемента.
Таким образом, решение пьезоэлектрических задач в модуле АРМ Structure3D было сведено к решению температурных задач.
Описание резонатора балочного типа
Чувствительным элементом датчика является резонатор, состоящий из вибратора, закрепленного в корпусе посредством подвески. Вибратор выполнен в виде балки из плавленого кварца квадратного поперечного сечения, на верхних гранях которой расположены пьезоэлементы возбуждения, а на нижних — пьезоэлементы отклика. Пьезоэлементы представляют собой тонкие пластины из пьезокерамики. Макет резонатора балочного типа показан на рис. 1.

Рис. 1. Экспериментальный макет резонатора балочного типа
Приложенное к верхним пьезоэлектрическим пластинам переменное электрическое напряжение вызывает в соответствии с обратным пьезоэффектом их циклические деформации растяжения-сжатия. В результате возникают изгибные колебания балки в вертикальной плоскости (в плоскости возбуждения), а в нижних пьезоэлементах — переменные механические напряжения, которые в соответствии с прямым пьезоэффектом индуцируют одинаковые по модулю электрические заряды. При повороте прибора вокруг продольной оси балки (оси чувствительности гироскопа) возникают инерционные силы Кориолиса, пропорциональные угловой скорости поворота и порождающие вторичные колебания балки в горизонтальной плоскости (плоскости отклика). В результате суперпозиции двух колебаний на пьезоэлементах отклика величины зарядов различаются, а возникающая разность потенциалов служит мерой измеряемой угловой скорости. При резонансе выходные сигналы возрастают примерно в Q раз по сравнению с квазистатическим режимом (Q — добротность резонатора).
При совпадении собственных частот колебаний в плоскости возбуждения и в плоскости отклика выходной сигнал возрастает в Q 2 раз. Последним обстоятельством объясняется необходимость исследования собственных частот.
Построение и анализ упрощенной модели резонатора
Стоит отметить, что в версии 9.3 разработчики из НТЦ АПМ добавили новую возможность — проведение некоторых видов расчетов непосредственно в 3D-редакторе — модуле АРМ Studio. Правда, возможность задания материалов реализована пока только для поверхностных моделей, но в перспективе, надеемся, это будет сделано и для объемных конечных элементов (солид-элементов).
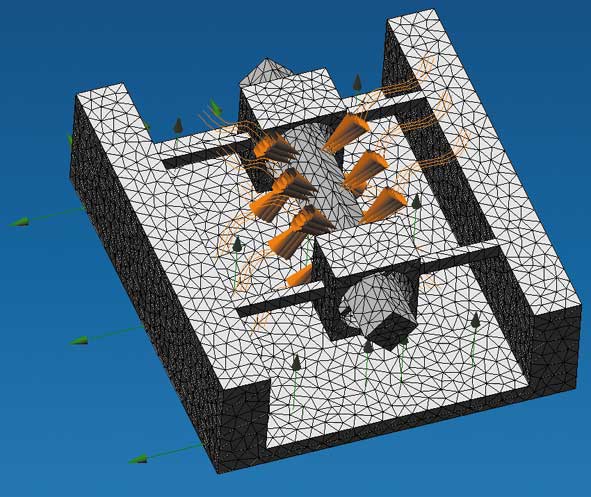
Рис. 2. Конечно-элементная упрощенная модель резонатора, полученная в 3D-редакторе APM Studio
На рис. 2 показана упрощенная конечно-элементная модель резонатора, созданная в редакторе APM Studio. Материал всех элементов модели — сталь (взята из базы данных материалов). Размеры балки — 36x4x4 мм. Воронкообразными стрелками желтого цвета показано задание электрического напряжения условной температуры на пьезоэлементы, а зелеными стрелками — заданное закрепление элементов такой балки.
Здесь же были рассчитаны собственные частоты и найдены собственные формы резонатора.
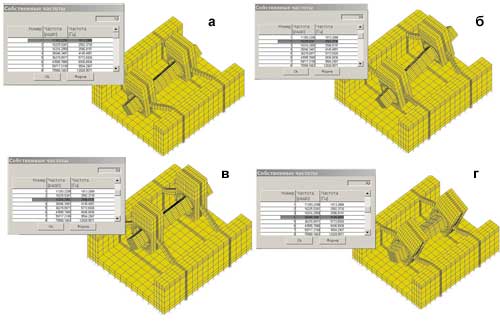
Рис. 3. Собственные формы колебаний упрощенной модели, полученные в результате расчета собственных частот в модуле APM Studio: а — 1-я собственная форма модели резонатора; б — 3-я собственная форма; в — 5-я собственная форма; г — 8-я собственная форма модели резонатора
На рис. 3 показаны наиболее интересные 1, 3, 5 и 8-я собственные формы соответственно. При 1-й и 3-й формах колебаний деформируются только элементы подвески, а балка резонатора смещается, как жесткое тело: в первом случае поступательно, а во втором — вращается подобно качелям.
Рабочим частотам отвечают: 5-я форма — возбуждение на частоте 14,629 кГц и 8-я форма — отклик на частоте 17,995 кГц. На рис. 6 показаны неподвижные зоны в районе узловых точек, через которые должны проходить оси стержней подвески.
Следует заметить, что для свободной балки с указанными свойствами теоретическое значение основной частоты изгиба по первой форме с двумя узлами составляет 16,063 кГц независимо от плоскости изгиба (в силу симметрии поперечного сечения). Отличие полученных собственных частот от теоретического значения определяется влиянием масс и упругости стержней подвески.
Отсюда видна необходимость максимально точного определения собственных частот для оптимизации конструкции, а также настройки автогенератора на частоту, вызывающую резонансные изгибные колебания вибратора в первичной плоскости.
Построение и анализ уточненной модели резонатора
Метод конечных элементов позволяет создать виртуальную модель, наиболее полно отражающую все особенности реальной конструкции. При этом можно, руководствуясь теоретическими положениями, модифицировать конструкцию до достижения равенства собственных частот. Модуль прочностного расчета APM Structure3D позволяет получить больше информации о собственных частотах конструкции, поэтому для уточненного анализа использовался именно он.
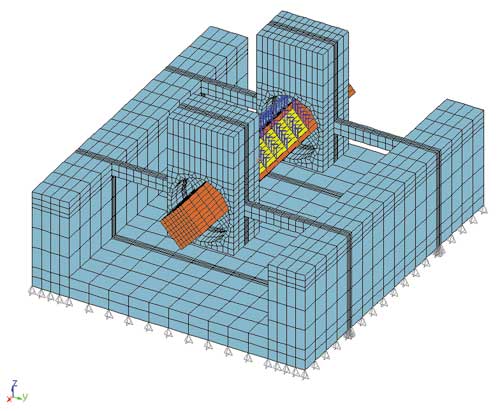
Рис. 4. Уточненная модель резонатора, выполненная в модуле APM Structure3D из восьмиузловых объемных элементов
На рис. 4 приведена уточненная модель резонатора, построенная в модуле прочностного расчета APM Structure3D, там же было произведено ее разбиение на восьмиузловые объемные конечные элементы (их получилось около 15 000). Затем модели были заданы закрепления отдельных узлов и присвоены параметры материалов, которые предварительно были добавлены в базу данных. Для уменьшения времени расчета конструкция модели была оптимизирована — корпус выполнялся из восьмиузловых объемных конечных элементов.
Для создания такой модели использовался персональный компьютер со следующими параметрами: частота процессора — 3 ГГц, объем оперативной памяти — 1024 Мбайт, емкость HDD — 200 Гбайт, операционная система Windows XP. Подготовка данных для расчета заняла около 5 часов.
Время расчета собственных частот составило около 20 мин. В результате было найдено девять собственных форм и соответствующих частот.
Результаты расчета собственных частот приведены на рис. 5-6.
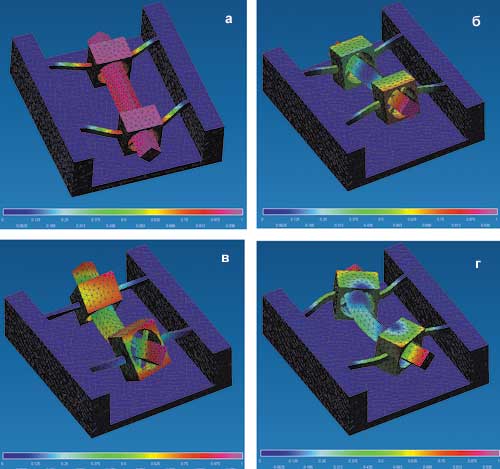
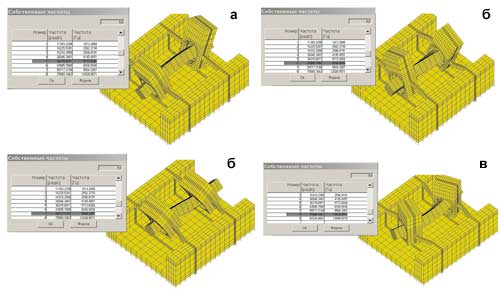
Рис. 5. Первые четыре низшие собственные формы уточненной модели резонатора, полученные в результате расчета собственных частот в модуле APM Structure3D: а — 1-я собственная форма модели резонатора; б — 2-я собственная форма; в — 3-я собственная форма; г — 4-я собственная форма модели резонатора
Рис. 6. Четыре высшие собственные формы уточненной модели резонатора: а — 5-я собственная форма модели резонатора; б — 6-я собственная форма; в — 7-я собственная форма; г — 8-я собственная форма модели резонатора
В ходе анализа собственных форм были выделены две, отвечающие частотам изгибных колебаний в первичной (f5 = 5,773 кГц) и вторичной (f8 = 12,029 кГц) плоскостях. Первые четыре собственные частоты не являются рабочими, так как они соответствуют деформациям подвески и корпуса и не связаны с изгибом балочного вибратора. В остальных формах наблюдаются деформации кручения вибратора.
Для проверки соответствия результатов расчета были проведены эксперименты с макетом, показанным на рис. 1. В ходе опытов было установлено, что разность между значениями собственных частот, полученных с использование МКЭ, и частот, определенных экспериментально, составляет от 3 до 15%, что свидетельствует о достаточно высокой точности расчетов. Осциллограмма свободных колебаний вибратора при возбуждении ступенчатым напряжением (меандром) частотой 118 Гц показана на рис. 7. Масштаб развертки составляет 1 мс/дел.
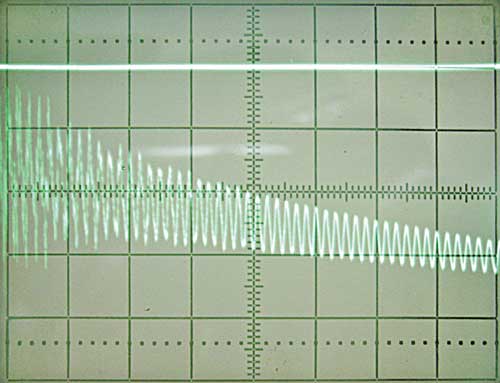
Рис. 7. Экспериментальная осциллограмма свободных колебаний резонатора
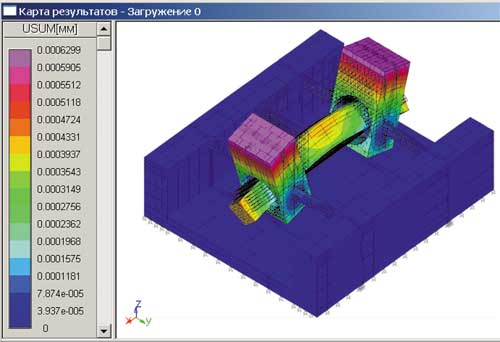
Рис. 8. Карта перемещений в модели резонатора по результатам статического расчета, выполненного в модуле APM Structure3D
Как можно видеть, частота свободных колебаний в вертикальной плоскости здесь составляет около 6 кГц, что отличается от полученной в результате расчета частоты f5 не более чем на 4%.
Статический расчет с использованием температурной аналогии
Для исследования напряженно-деформированного состояния элементов резонатора и оценки прогибов были проведены расчеты методом КЭ-модели, показанной на рис. 7, в статическом режиме с использованием температурной аналогии пьезоэффекта. Расчеты проводились в модуле APM Structure3D с заменой пьезоэлектрического коэффициента материала пьезоэлементов их температурным коэффициентом линейного расширения. Вместо возбуждающего напряжения в 100 В к пьезоэлементам прикладывалась температура в 100 °С. Для остальных материалов температурный коэффициент полагался равным нулю. Для определения термоупругих напряжений одновременно выполнялись «Статический расчет» и «Тепловой расчет».
Результаты расчета термоупругих напряжений и перемещений этой модели приведены на рис. 8-11.
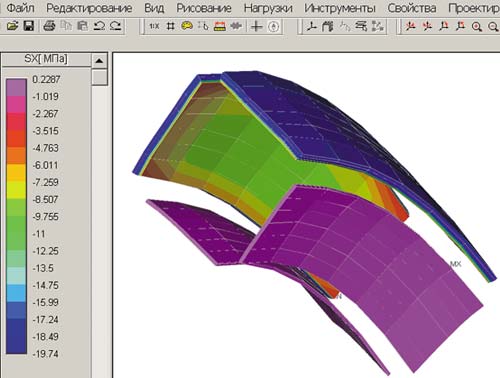
Рис. 9. Карта нормальных напряжений в пьезоэлементах возбуждения
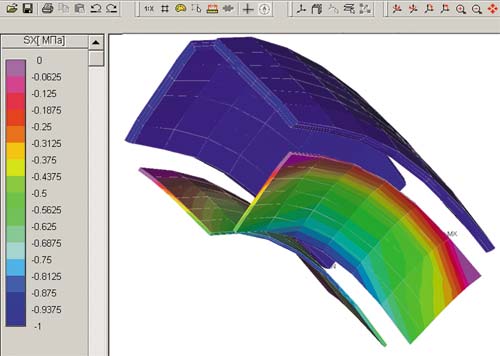
Рис. 10. Карта нормальных напряжений в пьезоэлементах отклика
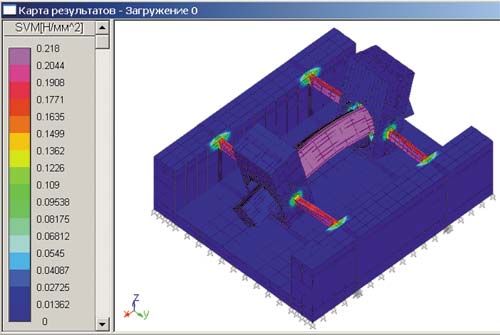
Рис. 11. Карта распределения эквивалентных (по Мизесу) напряжений в элементах резонатора
Вывод
С помощью системы АРМ WinMachine в редакторе APM Studio была создана с нуля трехмерная модель резонатора, а в модуле прочностного расчета APM Structure3D произведена серия расчетов частот собственных колебаний и статический расчет с учетом пьезоэффекта с заменой его температурным воздействием.
В заключение хочется отметить, что CAD/CAE-система АРМ WinMachine в очередной раз показала свои мощные возможности по моделированию и расчету таких объектов, как электромеханические устройства электронной техники. Наглядная визуализация результатов и простота работы позволили нам провести анализ нескольких моделей и подобрать частоты вынуждающей пьезоэлектрической силы, а также выдвинуть ряд предложений по оптимизации конструкции резонатора пьезогироскопа.
Хочется пожелать разработчикам этого программного продукта, чтобы они более полно удовлетворяли всевозрастающие требования пользователей, число которых неуклонно растет.
Александр Николаевич Виноградов
Канд. техн. наук, доцент. Работает в МИЭМ с 1971 года по настоящее время. По совместительству — ведущий научный сотрудник НИИ перспективных материалов и технологий (ГНУ «НИИ ПМТ») Московского государственного института электроники и математики.

Егор Владимирович Матвеев
Студент 5-го курса Московского государственного института электроники и математики (МИЭМ), техник ГНУ «НИИ ПМТ». Опыт работы с системой APM WinMachine — около трех лет.