Введение
В статье описаны подходы, применяемые при разработке пользовательского инструментария для проектирования моделей и узлов с изменяемым взаимным положением и задания геометрических ограничений движения элементов и узлов. Вместе с тем рассмотрена классификация элементов и узлов по типу «трансляции» ограничений подчиненным объектам и по характеру ограничений. Задача была решена в САПР К3 с использованием параметрического ядра C3D Solver.
C3D Solver дает возможность разработчикам программного обеспечения устанавливать зависимости между различными элементами геометрической модели. C3D Solver связывает элементы геометрической модели с помощью размеров и ограничений и обеспечивает сохранение заданных связей при изменении размеров, параметров модели, перемещении отдельных элементов модели или внесении иных изменений в геометрию модели.
Связи между объектами описываются геометрическими ограничениями, которые могут быть как размерными, задающими углы и расстояния, так и логическими, задающими совпадение, параллельность, перпендикулярность, касание. Геометрические ограничения могут накладываться на двумерные (2D) и трехмерные (3D) объекты.
Области применения C3D Solver:
- двумерные параметрические эскизы с управляющими размерами и ограничениями;
- позиционирование тел сборочной единицы с помощью сопряжений и размеров;
- перестроение модели с сохранением сопряжений после внесения изменений в модель;
- моделирование механизмов.
Постановка задачи
Одной из основных задач систем автоматизации проектных работ является решение геометрических задач, связанных с изменяемым взаимным положением узлов деталей и механизмов. Такого рода задачи обусловлены ужесточением требований, предъявляемых к модели конструкции. В рамках применения CALSтехнологий необходимо свести к минимуму натурное создание опытных образцов и автоматизировать все этапы жизненного цикла изделий и конструкций [1]. Одним из этапов жизненного цикла изделий является не только геометрическое, но и кинематическое проектирование.
В общем случае, задача моделирования движения частей механизмов сводится к задаче удовлетворения ограничений, поскольку все основные кинематические связи выражаются через набор геометрических ограничений, таких как совпадение, соосность, параллельность, перпендикулярность и т.д. Каждая кинематическая пара из такой системы ограничений имеет свою относительную степень свободы. При этом отдельный узел считается условно неподвижным, а сочленяемые с ним — условно подвижными. Все соединения в совокупности с учетом, что детали конструкции не должны сталкиваться, оставляют каждой детали механизма определенные рамки движения, например диапазон возможного перемещения одной детали относительно другой, ограничение угла поворота при вращении одной детали относительно другой и пр.
Однако реальные объекты проектирования имеют гораздо более сложную структуру, чем отдельные узлы или сочленения. Зачастую ограничения на движения тех или иных элементов конструкции определяются совокупностью узлов и механизмов. При этом на различных участках движения ограничения от одного из узлов оказывают более существенное влияние, чем ограничения от других узлов. На рис. 1 приведен пример обычной мебельной дверки как в закрытом, так и в открытом положении. Этот пример показывает, что в каждой конкретной точке траектории движения на элементы накладываются ограничения свободного перемещения.


Рис. 1. Пример движения с ограничениями
Как видно, движение верхней створки дверки определяется двумя узлами: верхними петлями и подъемным механизмом. Причем характер движения под влиянием каждого из механизмов в отдельности не сводим к совокупному влиянию. Так, например, если бы не было петель на верхней створке, сама створка могла бы совершать любое плоскопараллельное движение, ограничиваемое только диапазоном выдвижного механизма подъемника. Ограничения на угол поворота подъемника не существует. Использование же только петель без подъемника не наложит ограничений на угол поворота (строго говоря, петли имеют ограничение на угол поворота, но этот угол обычно составляет не меньше 110°, в то время как на рис. 1 угол открывания меньше 90°).
Что же касается нижней створки и ограничений в ее перемещении, то на нее оказывается гораздо более сложное влияние. На нее, помимо верхней створки, влияют петли, соединяющие створки.
Анализ существующих типовых кинематических узлов и механизмов показал, что в подавляющем большинстве используются механизмы рычажного типа. Геометрические основы систем моделирования таких механизмов описаны в работе В.Е. Турлапова [2].
Классификация ограничений и объектов
В реальных сборочных конструкциях таких взаимоограничений может быть достаточно много. При этом положение объектов вычисляется не только в начальном и конечном положении, но также и во всех промежуточных положениях.
Решить эту задачу в САПР К3 помогает параметрическое ядро C3D Solver, входящее в состав C3D Toolkit от компании C3D Labs [4]. Однако C3D Solver — это инструмент разработчика, а не конечного пользователя САПР. В системе К3 инструментарий решателя выведен на уровень пользователя. Задание ограничений на движение представляет собой запись информации в пользовательские атрибуты объектов.
Геометрические ограничения являются средством моделирования кинематических соединений. Например, шарнирное соединение, в котором участвует кинематическая пара дверной петли, оставляет подвижной части единственную степень свободы вращения. На языке ограничений такой механизм описывается двумя условиями: совпадение плоских граней и соосность цилиндрических граней. Таким образом, каждый узел механизма сообщает геометрическому решателю свое описание.
Далее будет рассмотрена концепция моделирования, которая опирается на определенный порядок организации сборки, где одни узлы кинематической цепочки подчинены другим. Несмотря на иерархический характер сборки, C3D Solver может обрабатывать такие модели как вариационные, где все детали, участвующие в системе ограничений, равноправны, что, в частности, позволяет решить обратную кинематическую задачу. Например, если приложить воздействие к дверной ручке, точно задав ей координаты в пространстве модели, можно вычислить положение остальных деталей сборки.
В САПР К3 объекты, подверженные влиянию ограничений на движение, делятся на три основных типа:
- сам по себе объект, который сам в себе содержит ограничение и сам же их «отрабатывает»;
- подчиненный объект — объект, который сам в себе информации о движении не содержит, а только лишь «отрабатывает» информацию, полученную извне;
- главный объект — объект, который сам не движется, но содержит и передает информацию о движении подчиненным объектам.
Также в САПР К3 представлены элементарные типы кинематических ограничений. Более сложные ограничения представляют собой совокупность элементарных (рис. 2).

Рис. 2. Примеры кинематических ограничений
Так, в приведенном нами примере объект «мебельная ручка» является подчиненным, поскольку сама ручка информацию о движении не содержит и только «отрабатывает» движение, полученное от других объектов. А объект «верхняя петля» (вернее, неподвижная часть петли) сама не движется, а «транслирует» информацию о движении другим объектам.
Кроме того, каждый объект, участвующий в перемещении, имеет следующие общие характеристики:
- общее (для данного объекта) время начала движения;
- общее (для данного объекта) время окончания движения;
- направление движения времени (объект «открывается» или «закрывается);
- количество «движений» — общее количество сдвигов и поворотов данного объекта.
Таким образом, каждый из объектов, участвующих в перемещении, может «присоединиться» к общему движению в тот или иной момент времени. При этом объект может совершать достаточно сложное движение из нескольких сдвигов и перемещений.
После общих характеристик для каждого объекта задаются движения, которые он должен совершить. Существует два типа элементарных движений: сдвиг и поворот, а следовательно, содержание информации об элементарном движении зависит от того, сдвиг это или поворот.
Решение поставленной задачи значительно упрощается при использовании параметрического подхода. В данном случае кинематические ограничения узлов нижних уровней формируют ограничения узлов верхних уровней структурного объекта. При этом использование механизмов репараметризации и депараметризации [3] позволяет динамически контролировать и вносить изменение в общую параметрическую модель объектов.
Математический аппарат
Положение каждого элемента и узла характеризуется его матрицей.
Существует три элементарных матричных преобразования: преобразование сдвига на вектор, преобразование поворота на угол, преобразование масштабирования. В нашем случае используются только преобразование сдвига и преобразование поворота.
C математической точки зрения, любое изделие представляет собой граф сборки [1], на который наложены параметрические связи [3], — рис. 3.
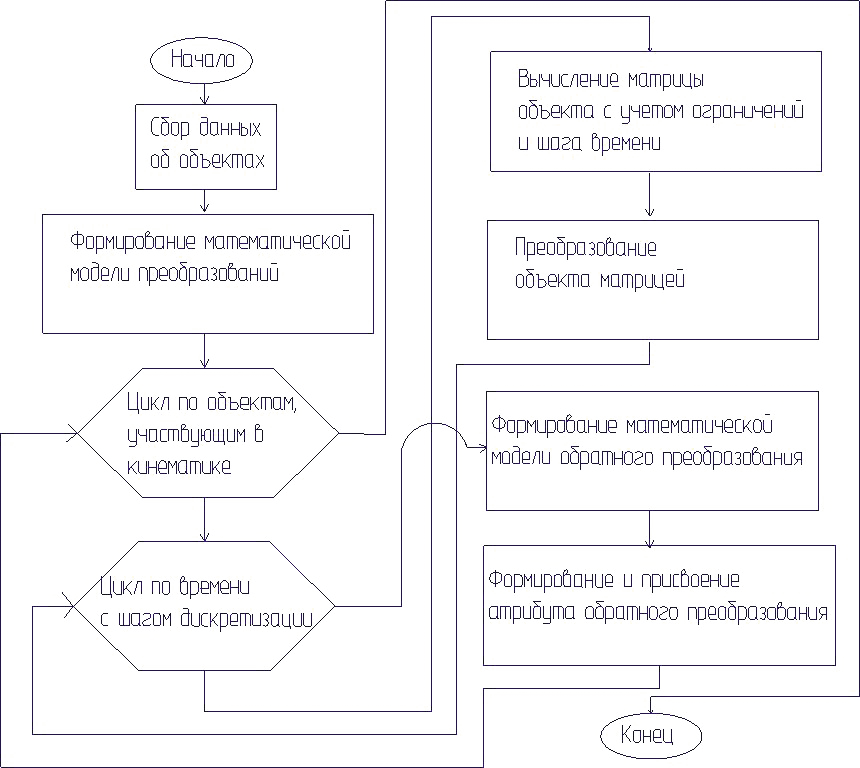
Рис. 3. Граф сборки модели
Данное утверждение целиком и полностью справедливо для формирования геометрии модели. В вершинах графа содержатся private и publicпараметры каждого отдельного узла.
Если же речь идет о формировании кинематической модели, то вершины графа также содержат набор кинематических ограничений и «транслируют» эти ограничения согласно концепции депараметризации и репараметризации. Ребра графа — это формирование матриц преобразования узлов более нижних уровней в зависимости от преобразования родительского узла и кинематических ограничений [2].
Изменение положения объекта — это, по сути, изменение его матрицы. С математической точки зрения, задача сводится к вычислению матрицы каждого из объектов.
Стоит особо отметить, что задание таких элементарных движений в системе К3 доступно пользователю. Однако на практике такое задание может показаться достаточно трудоемким. Кроме того, дополнительную сложность создает то, в какой системе координат нужно осуществлять преобразование. Строго говоря, все преобразования должны выполняться в системе координат «родительского» объекта, поскольку детали и узлы перемещаются не относительно себя, а относительно более крупного узла, в который они входят. А вот задавать сами параметры удобней в системе координат узла…
С целью упрощения решения этих задач разработчиками К3 написан алгоритм на макроязыке программы, который производит преобразование параметров перемещения деталей и узлов из собственной локальной системы координат в систему координат родительского узла (рис. 4). Дополнительно к этому стоит отметить, что в САПР К3 разработчиками включена достаточно большая библиотека типовых узлов и деталей с заданными ограничениями на движение элементов.
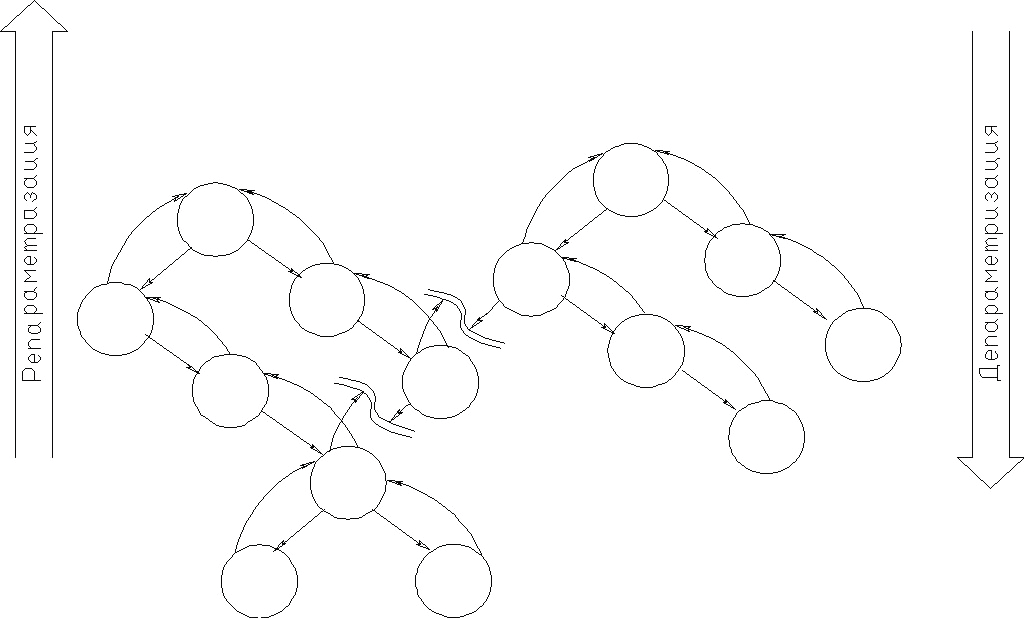
Рис. 4. Краткая блок-схема алгоритма
На практике при работе в САПР К3 конечному пользователю нет необходимости знать и понимать значение атрибута, содержащего информацию о перемещении того или иного объекта или его части. С точки зрения пользователя, в К3 реализован набор пользовательских функций, которые назначают, читают, изменяют возможные параметры движения объектов или узлов, накладывая ограничения на суммарное движение.
Выводы
В статье показано устройство модели САПР применительно к проектированию частей механизмов с изменяемым взаимным положением. Рассмотрено практическое применение модуля C3D Solver в САПР К3 моделирования сборочных конструкций и анализа их кинематики. Также рассмотрена классификация элементов и узлов по типу «трансляции» ограничений подчиненным объектам и по характеру ограничений. Показан пример использования методики для решения прикладной задачи, приведена классификация объектов по типу движения и по типу «трансляции» движения зависимым объектам.
Литература
- Ротков С.И. Разработка средств геометрического моделирования и компьютерной графики пространственных объектов для CALSтехнологий. Дисс. докт. техн. наук. Нижний Новгород: ННГАСУ, 05.01.01, 1999 г., 300 с.
- Турлапов В.Е. Геометрические основы систем моделирования кинематики пространственных рычажных механизмов. Дисс. докт. техн. наук. М.: МАИ, 05.01.01, 2003 г., 280 с.
- Ермаков Е.С. Принципы многоуровневой параметризации при формировании объектов. Дисс. канд. техн. наук, Ижевск: ИжГТУ, 05.13.12, 2008 г., 150 с.
- Сайт разработчика C3D Solver — компании C3D Labs: http://c3dlab


